-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Computational and Applied Mathematics
p-ISSN: 2165-8935 e-ISSN: 2165-8943
2014; 4(3): 61-76
doi:10.5923/j.ajcam.20140403.01
Optimal Control Applied to the Spread of Buruli Uclcer Disease
Ebenezer Bonyah 1, Isaac Dontwi 1, Farai Nyabadza 2
1Department of Mathematics, Kwame Nkumah University of Science and Technology, Kumasi, Ghana
2Department of Mathematical Science, University of Stellenbosch, Private Bag X1, Matieland, 7602, South Africa
Correspondence to: Ebenezer Bonyah , Department of Mathematics, Kwame Nkumah University of Science and Technology, Kumasi, Ghana.
| Email: |  |
Copyright © 2014 Scientific & Academic Publishing. All Rights Reserved.
Optimal control theory is applied to a system of ordinary differential equations modeling Buruli ulcer transmission in population. We apply controls on mass treatment, insecticide and mass education to minimize the number of infected hosts and infected vectors as well as infected fishes. The model takes into account human, water bug and fish populations as well as MU in the environment. The host, vector and small fish are all assumed constant. First, we investigated the existence and stability of equilibria of the model without control based on the basic reproduction ratio. We then, applied Pontryagins maximum principle to characterize the optimal control. The optimality system is determined and computed numerically for several scenarios.
Keywords: Mathematical model, Optimal control, Buruli ulcer, Basic reproduction ratio, Stability, Mass treatment, Insecticide
Cite this paper: Ebenezer Bonyah , Isaac Dontwi , Farai Nyabadza , Optimal Control Applied to the Spread of Buruli Uclcer Disease, American Journal of Computational and Applied Mathematics , Vol. 4 No. 3, 2014, pp. 61-76. doi: 10.5923/j.ajcam.20140403.01.
Article Outline
1. Introduction
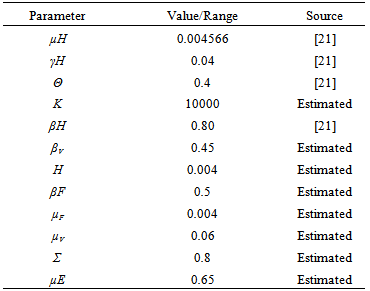
- Buruli ulcer is a debilitating human skin disease caused by Mycobacterium ulcerous [16].This infection is a neglected emerging disease that has recently been reported in some countries as the second most frequent mycobacterial disease in human tuberculosis [1]. A large number of lesions often result in scarring, contractual deformities amputations and disabilities [3]. In Africa, all ages and sexes are affected, but most cases of the disease occur in children between the ages of 4-15years [6]. It has emerged dramatically over the past two decades especially in Central and West Africa and has been confirmed by laboratory tests in 26 countries with reports in other countries around the world [2, 4]. Burului ulcer has been reported in over 30 countries mainly with tropical and subtropical climates but it may also occur in the same countries where it has not yet been recognized such as Burkina Faso and Guinea [2]. Notable contributing factors for Buruli ulcer outbreak include deforestation, eutrophication, dam construction, farming and habitat fragmentation. When treatments are delayed often in West Africa where due to lack of adequate knowledge about the disease they normally reported late, infections could lead to ulcerated lesions[16].When data from Ghana were analysed it was revealed that socioeconomic impact had a huge economic burden on affected countries. For example, gross domestic product per capital (Ghana) in 1998 was estimated at USD 399.41. The cost of surgical excisions of a large ulcer including 3 months inpatient expenses, transportation, food and income lost was USD 783. The current strategy of controlling the disease includes the use of drugs, surgery, heat, hyperbaric oxygen and traditional medicine. These are strong social economic ways to the burden of the BU disease, which in different ways affects fertility, population growth, saving and investment, absenteeism, stigmatization of women in adulthood for marriage and medical cost [19].Modeling of epidemiological phenomena has a very long story with the first model for smallpox formulated by Daniel Bernoulli in 1760. Mathematical modeling of the population models continues to provide vital insights into population behaviour and control. In the past years this has become an essential tool in understanding the dynamics of diseases, and the decision which has to do with process regarding intervention programs for controlling population and disease problems and in many countries. Similarly, different techniques have been employed to study vital optimal control problem related to dynamical systems. In particular, [10] developed a continuous model for malaria vector control with the objective of studying how genetically modified mosquitoes should be introduced in the environment using optimal control problem strategies. [13] applied optimal control theory to model malaria disease that includes treatment and vaccination with warning immaturity, to study the impact of a possible vaccination with treatment strategies in controlling the spread of malaria. Time- -depend-control strategies have been applied for the study of HIV model [11, 12] for strain tuberculosis models. [14] also examined SIR epidemiological models numerically and obtains controls that exert maximum efforts on some initial interval.To the best of our knowledge there is no single mathematical model available with optimal control theory application on BU diseases. In this study, we desire and analyze a Buruli ulcer disease transmission mathematical model. We study and determine the possible impact of optimal treatment and preventing on the spread of Buruli ulcer. Theoretically, we analyzed the stability properties. We also undertake a detailed qualitative optimal control analysis of the resulting model, and we determine the necessary conditions for optimal control of the disease using Pontryagins Maximum Principle in order to obtain optimal strategies for controlling the spread of the disease. The aim of this paper is to develop an optimal control that minimizes the number of Burului ulcer infected hosts, vector and fish with optimal cost of mass treatment and insecticides using Pontryagins Maximum Principle.This paper is arranged as follows; in Section 2, we formulate and establish the basic properties of the model. The steady states are determined and analysed for their stability in Section 3. Parameter estimation and sensitivity analysis are given in Section 4. Numerical results on the behavior of the model are also presented in this section. In Section 5 we present the application of the model to a real life situation and concluded in Section 6.
2. The Model and Its Analysis
2.1. Model Formulation
- Based on the described transmission dynamics of Buruli ulcer, we formulate a constant human population NH(t), the vector population of water bugs NV (t) and the fish population NF(t) at any time t. We consider SIR model for human population and SI model for both water bugs (vector) and fish .The total human population is divided into three epidemiological subclasses of those that are susceptible SH(t), the infected IH(t) and the recovered RH(t). Total population of vector (water bug) at any time t is divided into two subclasses to susceptible water bugs SV (t) and those that are infectious and can transmit the buruli ulcer to humans, IV (t). The total population reservoir of small fish is also divided into two compartments of susceptible fish SF(t) and infected fish IF(t). We also take into account the role played by environment and therefore introducing a compartment U, denoting the density of Mycobacterium ulcerans in the environment. We make the following basic assumptions:● Mycobacterium ulcerans is transferred only from vector ( water bug) to humans.● There is homogeneity of human, water bug and fish populations interactions.● Infected humans recover and can be re-infected with Mycobacterium ulcerans again. We thus have loss of immunity.● Fish are preyed on by the water bugs.● Susceptible host (human population) can be infected through biting by an infectious vector (water bug). We represent the effective biting rate that an infectious vector has to susceptible host as βH and the incidence of new infections transmitted by water bugs is expressed by standard incidence rate
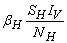 . One can interpret βH as the product of the biting frequency of the water bugs on humans, density of water bugs per human host and the probability that a bite will result in an infection.● Susceptible water bugs are infected at a rate
. One can interpret βH as the product of the biting frequency of the water bugs on humans, density of water bugs per human host and the probability that a bite will result in an infection.● Susceptible water bugs are infected at a rate 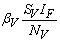 through predation of infected fish and
through predation of infected fish and 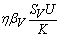 representing other sources in the environment. Here η differentiates the infectivity potential of the fish from that of the environment.● The vector population and the fish populations are assumed to be constant. The growth functions are respectively given by g(NV ) and g(NF). Without loss of generality, we can assume that the growth functions are given byg(NV) = µV NV and g(NF) = µFNF.It is important to note that logistic functions can be chosen as growth functions for richer dynamics. In this work, we however assume that the growth functions are linear.● There is a proposed hypothesis that environmental mycobacteria in the bottoms of swamps may be mechanically concentrated by small water-filtering organisms such as microphagous fish, snails, mosquito larvae, small crustaceans, and protozoa [5]. We thus assume that fish increase the environmental concentrations of Mycobacterium ulcerans at a rate σ.● The model does not include a potential route of direct contact with the bacterium in water.● The birth rate of the human population is directly proportional to the size of the human population.The possible interrelations between humans, the water bug and fish are represented by the schematic diagram below.The descriptions of the parameters that describe the flow rates between compartments are given in Table 1.
representing other sources in the environment. Here η differentiates the infectivity potential of the fish from that of the environment.● The vector population and the fish populations are assumed to be constant. The growth functions are respectively given by g(NV ) and g(NF). Without loss of generality, we can assume that the growth functions are given byg(NV) = µV NV and g(NF) = µFNF.It is important to note that logistic functions can be chosen as growth functions for richer dynamics. In this work, we however assume that the growth functions are linear.● There is a proposed hypothesis that environmental mycobacteria in the bottoms of swamps may be mechanically concentrated by small water-filtering organisms such as microphagous fish, snails, mosquito larvae, small crustaceans, and protozoa [5]. We thus assume that fish increase the environmental concentrations of Mycobacterium ulcerans at a rate σ.● The model does not include a potential route of direct contact with the bacterium in water.● The birth rate of the human population is directly proportional to the size of the human population.The possible interrelations between humans, the water bug and fish are represented by the schematic diagram below.The descriptions of the parameters that describe the flow rates between compartments are given in Table 1.
|
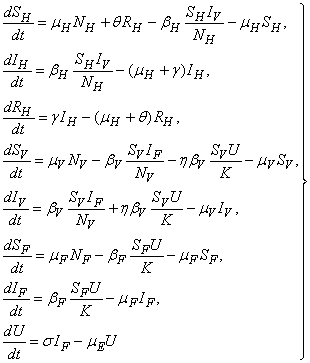 | (1) |
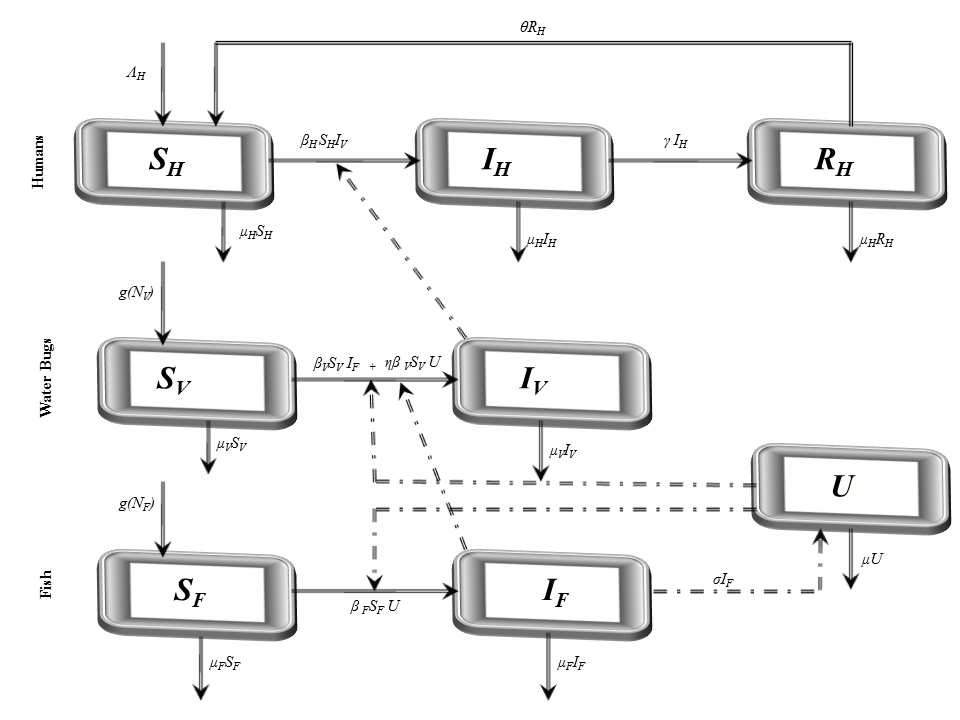 | Figure 1. Proposed transmission dynamics of the Buruli ulcer among fish, the water bug and humans |
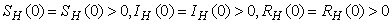
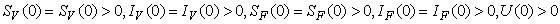 .The region of biological interest of model (1) is
.The region of biological interest of model (1) is 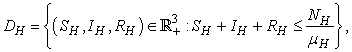
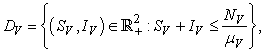
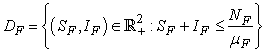 and
and 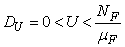
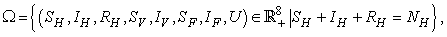 where
where 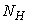 is constant.We note that model (1) is well positioned in the non-negative region
is constant.We note that model (1) is well positioned in the non-negative region 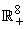 for the fact that the vector and fish as well as the environment do not point to the exterior. By providing an initial condition in the region, then we can define solution for all time
for the fact that the vector and fish as well as the environment do not point to the exterior. By providing an initial condition in the region, then we can define solution for all time  and remains in the region.
and remains in the region. 2.2. Positivity of the Solution
- We show that for any non-negative initial conditions of the system (1), the solutions still remain non-negative for all
 . We desire to prove that all necessary state variables in the system (1) remain non-negative and also the solutions of the system with positive initial conditions will stay positive for all
. We desire to prove that all necessary state variables in the system (1) remain non-negative and also the solutions of the system with positive initial conditions will stay positive for all 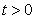 . We therefore, propose the following lemma.Lemma 1. Given that the initial conditions of the system (1) are positive, the solutions
. We therefore, propose the following lemma.Lemma 1. Given that the initial conditions of the system (1) are positive, the solutions 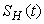 ,
,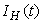 ,
,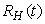 ,
,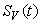 ,
,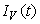 ,
, 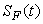 ,
, 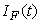 and
and 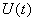 are non-negative for all
are non-negative for all 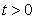 Proof. Given that
Proof. Given that 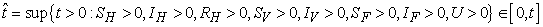 .More precisely
.More precisely 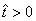 , and it implies directly from the first equation of the system (1) that
, and it implies directly from the first equation of the system (1) that 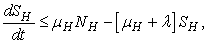 where
where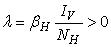 .We therefore have
.We therefore have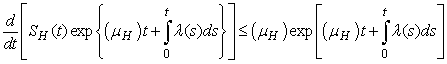 .Thus
.Thus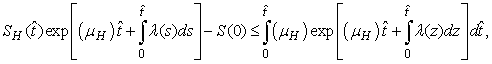 and that
and that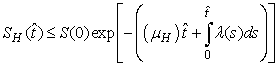
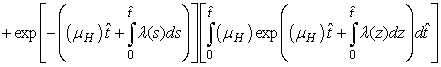 The right hand of (3) is obviously positive. Therefore, the solution
The right hand of (3) is obviously positive. Therefore, the solution 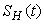 will at any given instance be positive. In examining the second equation of 1,
will at any given instance be positive. In examining the second equation of 1,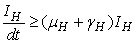
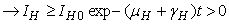 Similarly, it can be determined that
Similarly, it can be determined that 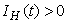 ,
,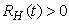 ,
,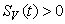 ,
,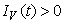 ,
,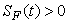 ,
,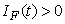 and
and 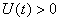 for all
for all 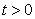 , and this leads to the completion of the proof.
, and this leads to the completion of the proof.3. Steady States and the Model Reproduction Number
- In this section, We compute the equilibrium points by equating the right side of model (1) to zero. This direct computation indicates that model (1) always possesses a disease free equilibrium point
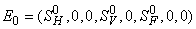 where
where 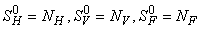 and a unique endemic equilibrium
and a unique endemic equilibrium 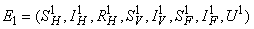 in Ω where
in Ω where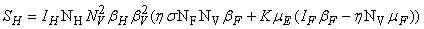
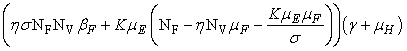
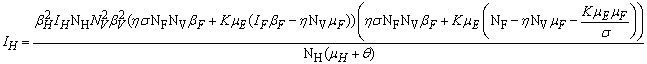
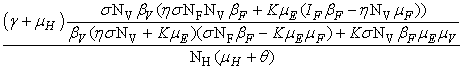
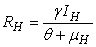
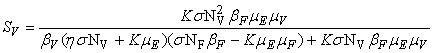
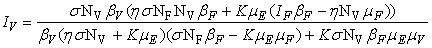
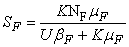
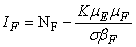
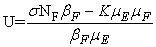
3.1. The Model Reproduction Number
- Basic reproduction ratio is the expected numbers of secondary cases of infection per primary case of infection in a virgin population during the infectious period of primary case [17]. By applying the next generation operator approach [18], we represent F and V respectively as matrices for the new infections generated and the transition terms we get
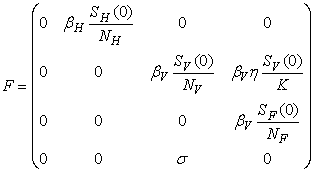 and
and 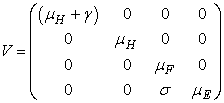
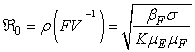 The basic reproduction number ℜ0 is expressed as the spectral radius of the matrix FV−1 and therefore
The basic reproduction number ℜ0 is expressed as the spectral radius of the matrix FV−1 and therefore 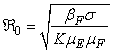 . The model reproduction number is determined by fish population and the density of Mycobacterium ulcerans in the environment. The reproduction number of the model (1) appears to be in ascendancy linearly with shedding rate of MU into the environment and effective contact rate between fish and MU. The spread of BU from model (1) does not depend on humans and the vector.
. The model reproduction number is determined by fish population and the density of Mycobacterium ulcerans in the environment. The reproduction number of the model (1) appears to be in ascendancy linearly with shedding rate of MU into the environment and effective contact rate between fish and MU. The spread of BU from model (1) does not depend on humans and the vector.3.2. Stability of the Disease Free Equilibrium
- Theorem 1. The disease free equilibrium
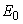 whenever it exists is locally asymptotically stable if
whenever it exists is locally asymptotically stable if 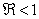 and unstable otherwiseThe Jacobian matrix of model (1) at the equilibrium point E0 is expressed by
and unstable otherwiseThe Jacobian matrix of model (1) at the equilibrium point E0 is expressed by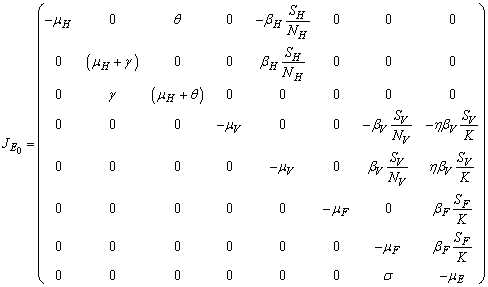 It can be observed that the eigenvalues of
It can be observed that the eigenvalues of 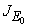 are (µH + γ),(σ + µH),−µF,−µH,−µV ,−µV and the roots of quadratic equation
are (µH + γ),(σ + µH),−µF,−µH,−µV ,−µV and the roots of quadratic equation 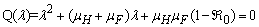 . The computational results of Q(λ) = 0 shows to have negative parts only if
. The computational results of Q(λ) = 0 shows to have negative parts only if 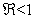 . We can therefore make a conclusion that the disease free equilibrium is locally asymptotically stable whenever
. We can therefore make a conclusion that the disease free equilibrium is locally asymptotically stable whenever 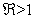 .
.3.3. Stability of the Endemic Equilibrium
- We examine the local geometric characteristics of the endemic equilibrium of model (1). We state the following theorem:Theorem 2. If
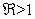 the endemic equilibrium point
the endemic equilibrium point 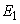 model (1), is locally asymptotically stable.However, it is difficult to deal with stability of endemic equilibrium
model (1), is locally asymptotically stable.However, it is difficult to deal with stability of endemic equilibrium 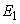 analytically because it contains a quadratic equation. By numerical approach, the endemic equilibrium is locally asymptotically stable. This is depicted in 2. We apply three different initial conditions for the simulation. Those orbits shown to be the same point as time evolve.
analytically because it contains a quadratic equation. By numerical approach, the endemic equilibrium is locally asymptotically stable. This is depicted in 2. We apply three different initial conditions for the simulation. Those orbits shown to be the same point as time evolve.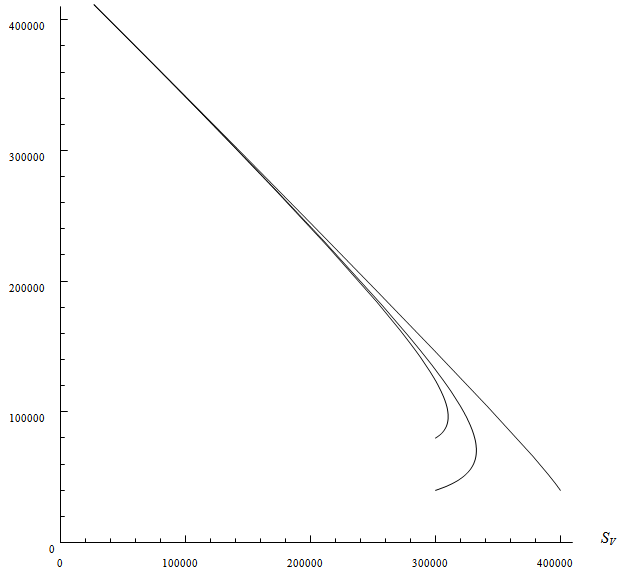 | Figure 2. Shows phase potrait of model (1) in SV — IV plane |
4. Analysis of Optimal Control
- Our state system is the following system of eight ordinary differential equations
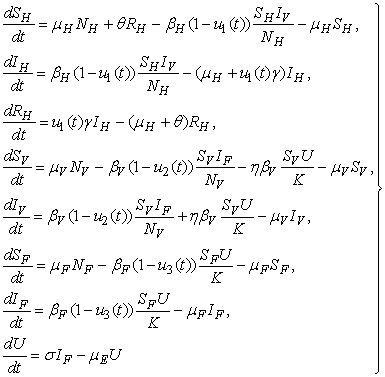 | (2) |
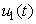 where
where 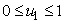 , deals with reducing the exposure of susceptible humans to those infected water bugs. This can be achieved by using insecticides and preventing the exposure of the human body from biting by water bugs. The control
, deals with reducing the exposure of susceptible humans to those infected water bugs. This can be achieved by using insecticides and preventing the exposure of the human body from biting by water bugs. The control 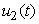
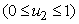 , models the efforts needed in bringing down the infection the water bugs and fishes. The last control
, models the efforts needed in bringing down the infection the water bugs and fishes. The last control 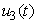
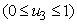 examines the efforts required in reducing the infection between the water bugs and the environment. In order to achieve a successful control of BU, the effort is needed in the determination of the infected and also strictly putting measures to reduce it.The objective is to minimize the number of infected humans in a settlement
examines the efforts required in reducing the infection between the water bugs and the environment. In order to achieve a successful control of BU, the effort is needed in the determination of the infected and also strictly putting measures to reduce it.The objective is to minimize the number of infected humans in a settlement 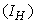 while maintaining the cost associated to control
while maintaining the cost associated to control 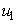 ,
, 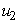 and
and 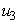 as much as possible. Therefore, we seek to minimize the number of Buruli ulcer infected hosts and cost of employing mass treatment, insecticide controls and reducing the number of infected fishes. Our optimal control problem with objectives function is expressed as
as much as possible. Therefore, we seek to minimize the number of Buruli ulcer infected hosts and cost of employing mass treatment, insecticide controls and reducing the number of infected fishes. Our optimal control problem with objectives function is expressed as 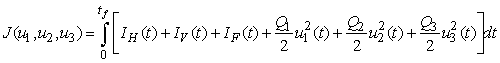 | (4) |
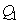 ,
,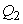 and
and 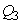 are the weighting constants for the mass treatment human host, insecticide activities and mass treatment for infectious fishes are nonlinear and are of quadratic forms.We therefore, seek an optimal control
are the weighting constants for the mass treatment human host, insecticide activities and mass treatment for infectious fishes are nonlinear and are of quadratic forms.We therefore, seek an optimal control 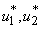 and
and 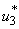 such that
such that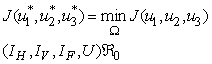 | (4) |
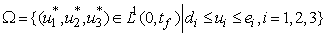 ,We analyze model 3, in other words model of the spread of Buruli ulcer in population applying optimal perspective. We take into account the objective function 4 to model 3. Pontryagins Maximum Principle will be employed to determine the optimal control
,We analyze model 3, in other words model of the spread of Buruli ulcer in population applying optimal perspective. We take into account the objective function 4 to model 3. Pontryagins Maximum Principle will be employed to determine the optimal control 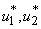 and
and 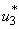 with necessary conditions. The necessary conditions to establish optimal control
with necessary conditions. The necessary conditions to establish optimal control 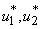 and
and 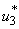 that meet condition 5 and its constraint model 3 will be determined by applying Pontryagins Maximum Principle (Pontryagin). The principle changes (3), 4 and 5 into a problem of minimizing pointwise a Hamiltonian, H, with respect to
that meet condition 5 and its constraint model 3 will be determined by applying Pontryagins Maximum Principle (Pontryagin). The principle changes (3), 4 and 5 into a problem of minimizing pointwise a Hamiltonian, H, with respect to 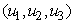 , simply
, simply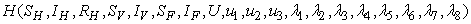
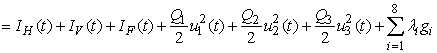 where
where 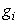 is the right hand side of the differential equations of the ith state variable. By using Pontryagin’s Maximum Principle and the existence of results obtained for optimal control, we achieve Theorem 3. There exists an optimal control
is the right hand side of the differential equations of the ith state variable. By using Pontryagin’s Maximum Principle and the existence of results obtained for optimal control, we achieve Theorem 3. There exists an optimal control 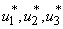 and corresponding solution,
and corresponding solution, 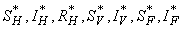 and
and 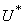 , that minimizes
, that minimizes 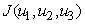 over
over  . Furthermore, there exist adjoint functions,
. Furthermore, there exist adjoint functions, 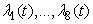 , such that
, such that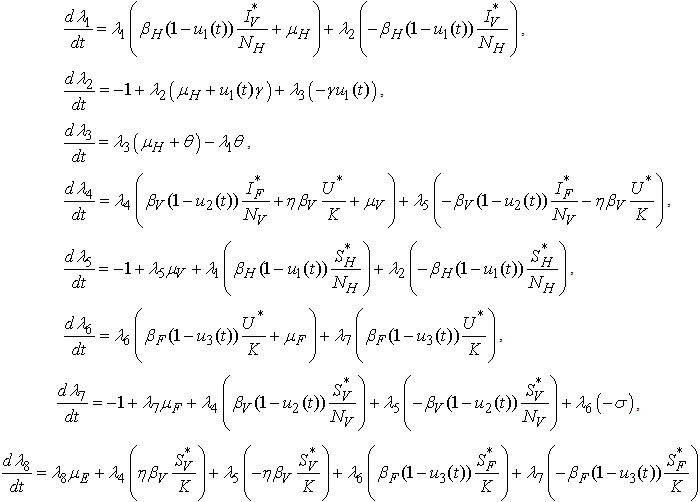 | (6) |
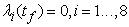 | (7) |
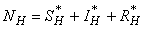 ,
,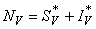 ,
,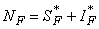 ,
, 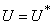 Theorem 4. The optimal control
Theorem 4. The optimal control 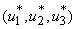 that minimizes
that minimizes 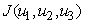 over
over 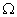 is expressed as
is expressed as 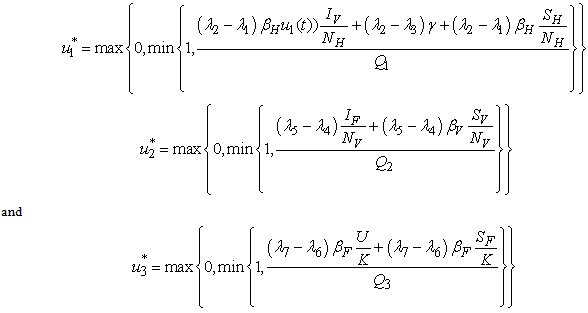 | (8) |
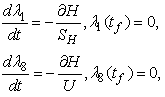 | (9) |
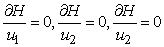 And determine the values for
And determine the values for 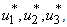 subject to the constraints, the characterizations (8) can be obtained. We illustrate the characterization of
subject to the constraints, the characterizations (8) can be obtained. We illustrate the characterization of 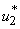 , we obtain
, we obtain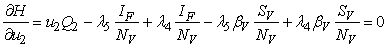
- By considering the bounds on
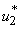 , we have the characteristics of
, we have the characteristics of 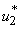 in 8. By the fact that there is a priori boundedness of the state and adjoint functions and the resulting Lipschitz structure of the ODEs, we get the uniqueness of the optimal control for small value of tf. The uniqueness of the optimal control based on the uniqueness of the optimality system, which is made up of 3 and 6, 7 with characterization 8. In order to guarantee the uniqueness of the optimal system, we put a restriction on the length of the time interval. The restriction on the length of time is as a result of opposite orientation of 3, 6 and 7. The stated problem contains the initial values and the adjoint problem contains final values.
in 8. By the fact that there is a priori boundedness of the state and adjoint functions and the resulting Lipschitz structure of the ODEs, we get the uniqueness of the optimal control for small value of tf. The uniqueness of the optimal control based on the uniqueness of the optimality system, which is made up of 3 and 6, 7 with characterization 8. In order to guarantee the uniqueness of the optimal system, we put a restriction on the length of the time interval. The restriction on the length of time is as a result of opposite orientation of 3, 6 and 7. The stated problem contains the initial values and the adjoint problem contains final values.5. Numerical Results
- In this section, we study numerically an optimal treatment strategy of our Buruli ulcer dynamics model. We solve the optimal control problem using an iterative scheme derived by [24].
|
5.1. Mass Treatment Control
- In this section, we consider only control
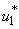 on mass treatment and both control
on mass treatment and both control 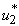 and
and 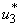 are set zero. The profile of the optimal control
are set zero. The profile of the optimal control 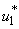 is depicted in Figure 5.1 (a). In order to do away with Buruli ulcer disease in 100 days, the treatment should be held intensively almost 100 days. By applying optimal control
is depicted in Figure 5.1 (a). In order to do away with Buruli ulcer disease in 100 days, the treatment should be held intensively almost 100 days. By applying optimal control 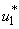 in Figure 5.1(a), we show the dynamics of infected humans, water bug, small fishes and Mycobacterium in the environment as observed in Figure 5.1(b, c,d, e) respectively. These numbers increase without optimal control
in Figure 5.1(a), we show the dynamics of infected humans, water bug, small fishes and Mycobacterium in the environment as observed in Figure 5.1(b, c,d, e) respectively. These numbers increase without optimal control 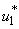 and that is to say if there is no mass treatment. It is interesting to observe from Figure 5.1 (c) that without the mass treatment the number of infected water bug decreases. However, the addition of this control
and that is to say if there is no mass treatment. It is interesting to observe from Figure 5.1 (c) that without the mass treatment the number of infected water bug decreases. However, the addition of this control 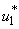 increases the rate of the reduction of the infection and slows the reduction otherwise.
increases the rate of the reduction of the infection and slows the reduction otherwise.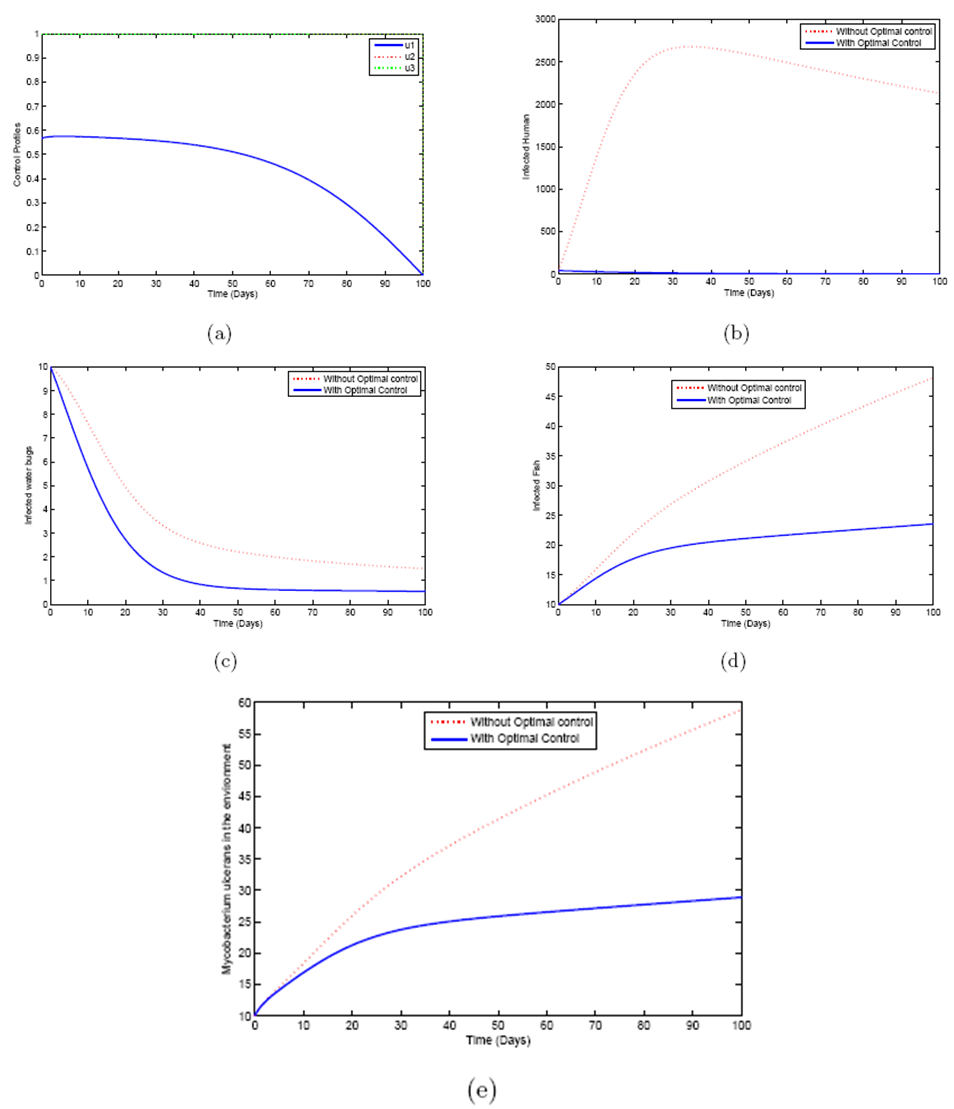 | Figure 5.1. Shows the profile of the optimal control u1 and optimal solution for infected humans, water bugs, small fish and MU in environment  via mass treatment only via mass treatment only |
5.2. Insecticide Control
- In this regard, we set both mass treatment control
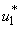 and mass education control
and mass education control 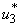 we then activate only
we then activate only 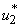 which is the insecticide as shown in Figure 5.2 (a). We show the profile of the optimal control
which is the insecticide as shown in Figure 5.2 (a). We show the profile of the optimal control 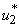 on insecticide (Figure 5.2(a)). It is observed in Figure 5.2 (b) that the number of infected humans drastically decreases with the application of insecticide control. This situation reverses without the control
on insecticide (Figure 5.2(a)). It is observed in Figure 5.2 (b) that the number of infected humans drastically decreases with the application of insecticide control. This situation reverses without the control 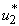 . In Figure 5.2 (c), the infected water bug reduces without the control
. In Figure 5.2 (c), the infected water bug reduces without the control 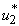 but with the control the reduction is higher. This process reduces without the application of insecticide. Figure 5.2 (d) depicts that infected small fish reduces with insecticide control
but with the control the reduction is higher. This process reduces without the application of insecticide. Figure 5.2 (d) depicts that infected small fish reduces with insecticide control 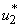 and increases without the control
and increases without the control 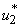 . We also observed in Figure 5.2(e) that the shedding of MU in the environment decreases with insecticide control
. We also observed in Figure 5.2(e) that the shedding of MU in the environment decreases with insecticide control 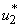 and increases in the environment without the control. That is to say, increase in shedding of MU in the environment.
and increases in the environment without the control. That is to say, increase in shedding of MU in the environment. 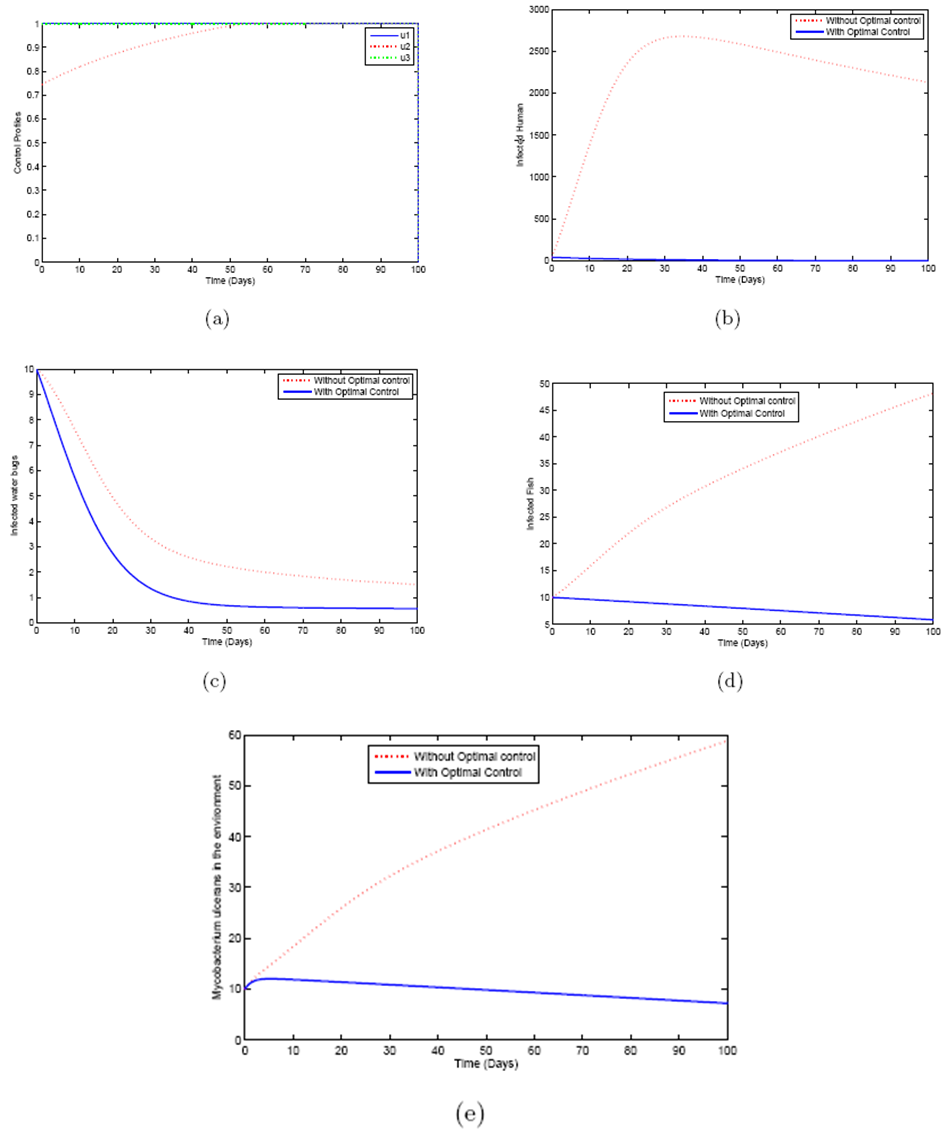 | Figure 5.2. Shows the profile of the optimal control u2 and optimal solution for infected humans,water bugs, small fish and MU in environment 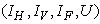 via insecticide application only via insecticide application only |
5.3. Mass Education
- In this scenario, we activate only the control
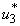 on mass education while both controls
on mass education while both controls 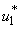 and
and 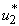 are set to zero. Figure 5.3 (a) depicts optimal control
are set to zero. Figure 5.3 (a) depicts optimal control 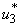 . In order to eliminate BU in 100 days, the mass education must be carried out intensively for almost 100 days as observed in Figure 5.3(a). In Figure 5.3 (b), the number of infected humans decreases drastically with control
. In order to eliminate BU in 100 days, the mass education must be carried out intensively for almost 100 days as observed in Figure 5.3(a). In Figure 5.3 (b), the number of infected humans decreases drastically with control 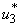 . That is to say, mass education and situation increase without mass education control
. That is to say, mass education and situation increase without mass education control 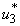 . Interestingly, in Figure 5.3 (c) infected water bugs decreases sharply with mass education which is control
. Interestingly, in Figure 5.3 (c) infected water bugs decreases sharply with mass education which is control 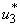 and infected water bugs increase otherwise. Figure 5(d) depicts that infected small fishes decrease with mass education control
and infected water bugs increase otherwise. Figure 5(d) depicts that infected small fishes decrease with mass education control 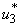 and increase with the control
and increase with the control 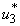 . We observed in Figure 5.3(e) that the shedding of MU in the environment reduces with control
. We observed in Figure 5.3(e) that the shedding of MU in the environment reduces with control 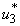 that is to say mass education and the situation reverses without the mass education.
that is to say mass education and the situation reverses without the mass education. 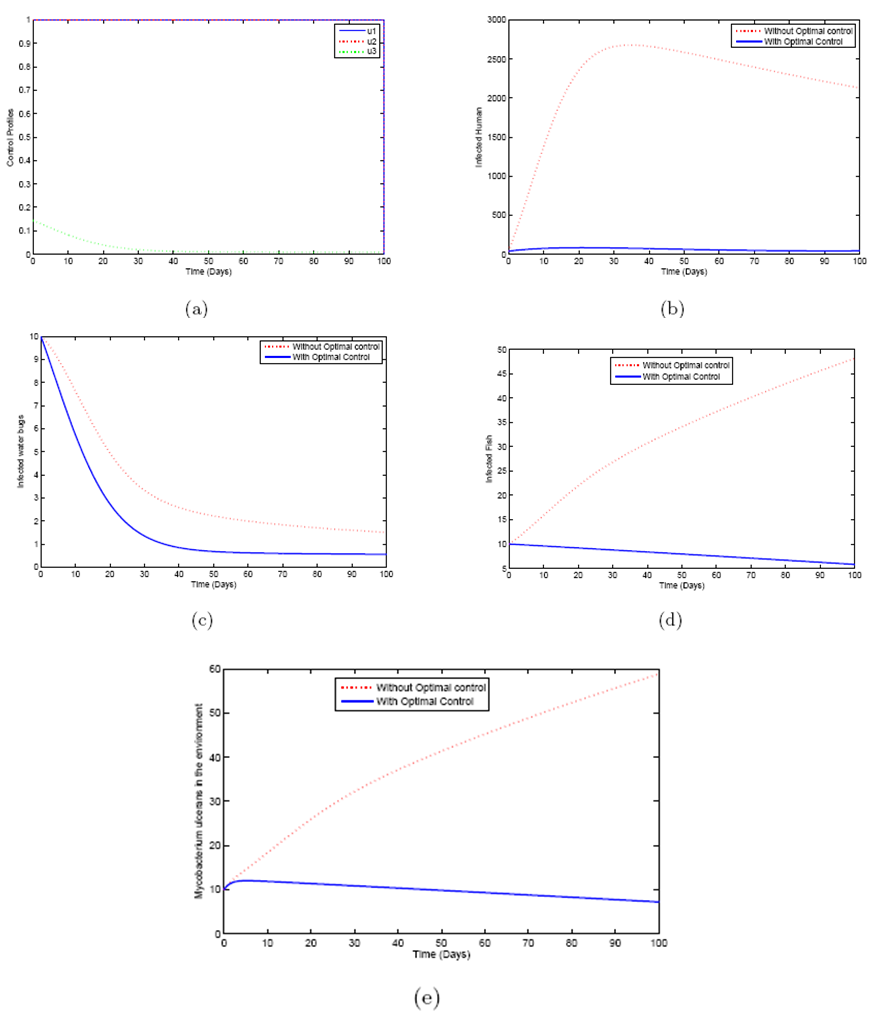 | Figure 5.3. Shows the profile of the optimal control u3 and optimal solution for infected humans, water bugs, small fish and MU in environment 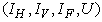 via mass education only via mass education only |
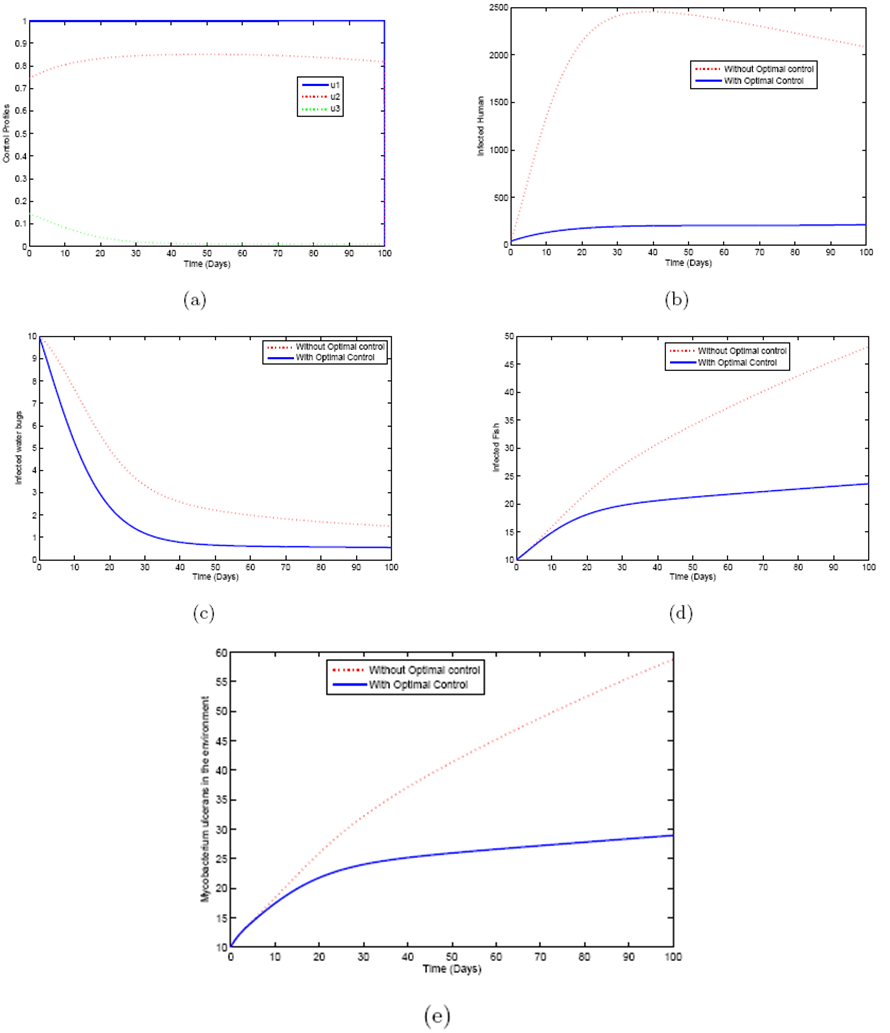
5.4. Mass Treatment, Insecticide Control and Mass Education
- In this perspective, the mass control
 , the insecticide control
, the insecticide control 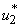 and mass education
and mass education 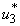 all activated to optimize the objective function J. We show the profile of optimal control
all activated to optimize the objective function J. We show the profile of optimal control 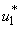
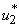 and
and 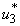 in Figure 5.4 (a). By using the optimal control
in Figure 5.4 (a). By using the optimal control 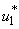 and
and 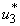 as observed in Figure 6(a), the dynamics infected humans, water bugs, small fish and MU in the environment are depicted in the Figure 5.4(b, c, d, e) respectively. In general, we observed that infected humans as seen in Figure 5.4 (b) decrease with the activation of all the controls. That is, to say
as observed in Figure 6(a), the dynamics infected humans, water bugs, small fish and MU in the environment are depicted in the Figure 5.4(b, c, d, e) respectively. In general, we observed that infected humans as seen in Figure 5.4 (b) decrease with the activation of all the controls. That is, to say 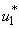 ,
, 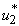 and
and 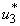 . Similarly in Figure 5.4 (c,d,e) we can see that the activation of controls
. Similarly in Figure 5.4 (c,d,e) we can see that the activation of controls 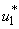 ,
, 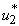 and
and 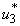 . In other words the mass treatment, insecticide and mass education reduce the spread of Buruli ulcer disease. In the absence of these combinations of controls, the number of infections within respective classes increases.
. In other words the mass treatment, insecticide and mass education reduce the spread of Buruli ulcer disease. In the absence of these combinations of controls, the number of infections within respective classes increases.6. Conclusions
- In this study, we derived and analyzed a deterministic model for the spread of Buruli ulcer that includes mass treatment, insecticide and mass education. We determine the basic reproduction ratio
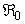 . This ratio depicts the existence and the stability of the equilibra of the model. Applying optimal control strategy, we find a solution to the eradication of BU disease in a finite time. By observing the numerical results, we can conclude that the combination of all the control
. This ratio depicts the existence and the stability of the equilibra of the model. Applying optimal control strategy, we find a solution to the eradication of BU disease in a finite time. By observing the numerical results, we can conclude that the combination of all the control 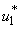 ,
, 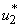 and
and 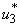 are capable of helping reduce the number of infected humans, water bugs, small fishes and MU in the environment.
are capable of helping reduce the number of infected humans, water bugs, small fishes and MU in the environment. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML
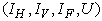 via mass treatment, insecticide application and mass education
via mass treatment, insecticide application and mass education