A. Y. Gital 1, 2, M. Abdulhameed 3, C. Haruna 4, M. S. Adamu 2, B. M. Abdulhamid 2, A. S. Aliyu 5
1Department of Computer Science, Universiti Teknologi Malaysia
2Mathematical Sciences Programme, Abubakar Tafawa University Bauchi-Nigeria
3Department of Mathematics, Universiti Tun Hussein Onn, Malaysia
4Artificial Intelligence Department, University of Malaya, Kuala Lumpur-Malaysia
5Department of Physics, Nassarawa State University, Keffi-Nigeria
Correspondence to: A. Y. Gital , Department of Computer Science, Universiti Teknologi Malaysia.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
In this Paper, the analytical solutions for the velocity and temperature profiles have been obtained in explicit forms for the Couette flow of a third grade fluid between two porous parallel plates. The obtained velocity and temperature profile are compared with the existing analytical solutions for a third grade fluid between parallel non-porous plates. It is found that the present results are in excellent agreement with the existing analytical solutions. Graphs representing the solutions are discussed, and appropriate conclusions drawn.
Keywords:
Third grade fluid, Porous plate, Analytical solution
Cite this paper: A. Y. Gital , M. Abdulhameed , C. Haruna , M. S. Adamu , B. M. Abdulhamid , A. S. Aliyu , Couette Flow of Third Grade Fluid between Parallel Porous Plates, American Journal of Computational and Applied Mathematics , Vol. 4 No. 2, 2014, pp. 33-44. doi: 10.5923/j.ajcam.20140402.01.
1. Introduction
The present study deals with the problem of heat transfer for the Couette flow of a third grade fluid between two parallel porous plates. Analytical solutions for the velocity and temperature profiles have been obtained in explicit forms. The related studies in the recent years dealing with third grade fluids are [1-5].Many models described by nonlinear differential equations of real life problems are difficult to solve either analytically or numerically. Much effort have been made in the literature for different techniques to make the nonlinear model solvable. Among the methods that have been employed to solve nonlinear models are related to Adomian decomposition method (ADM) [6], Variation iterative method (VIM) [7], spectral collocation method [8], homotopy analysis method (HAM) [9], homotopy perturbation method (HPM) [10], optimal homotopy asymptotic method (OHAM) [11], etc.In the present investigation, we construct analytical approximate solutions of the governing problem of heat transfer for the Couette flow of a third grade between two parallel porous plates using optimal homotopy asymptotic method (OHAM). The results reveal that the OHAM is valid not only for weakly nonlinear equations, but also for strongly nonlinear ones. Effects of the viscoelastic parameter and the suction/injection on velocity and temperature profiles are shown graphically.
2. Mathematical Model
For Couette flow problem, the lower plate is stationary and the upper plate is moving with a constant velocity 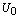 and the effect constant pressure gradient is neglected. The movement of fluid is solely due to motion of the upper plate. The fluid is brought into motion through the action of viscous stress at the plate. The temperature of the lower plate is maintained at
and the effect constant pressure gradient is neglected. The movement of fluid is solely due to motion of the upper plate. The fluid is brought into motion through the action of viscous stress at the plate. The temperature of the lower plate is maintained at 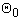 and that of the upper plate at
and that of the upper plate at 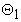 . Mathematical model of the present flow problem are formulated as below:
. Mathematical model of the present flow problem are formulated as below: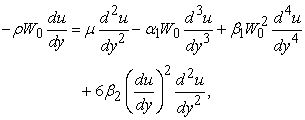 | (1) |
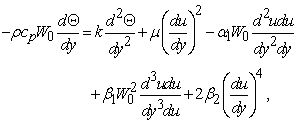 | (2) |
subject to the boundary condition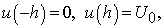 | (3) |
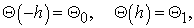 | (4) |
Where 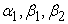 are the material moduli,
are the material moduli, 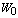 is the sunction/injection parameter,
is the sunction/injection parameter, 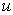 fluid velocity,
fluid velocity,  is the fluid temperature,
is the fluid temperature, 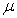 is the fluid viscosity,
is the fluid viscosity, 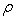 is the fluid density,
is the fluid density, 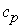 is the specific heat capicity and
is the specific heat capicity and 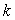 is the thermal conductivity.Introducing the dimensionless parameters
is the thermal conductivity.Introducing the dimensionless parameters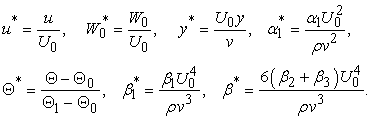 | (5) |
the non-dimensional problem, after dropping the asterisks, Eq. (1), (2) and boundary conditions (3) and (4) becomes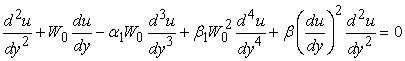 | (6) |
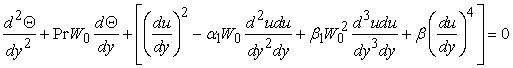 | (7) |
 | (8) |
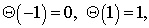 | (9) |
where 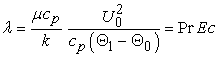 , Pr is the Prandtl number, Ec is the Eckert number and λ is the Brinkman number.
, Pr is the Prandtl number, Ec is the Eckert number and λ is the Brinkman number.
3. Basic Idea of the Optimal Homotopy Asymptotic Method (OHAM)
We classifying the equations to solved for velocity u and temperature Θ: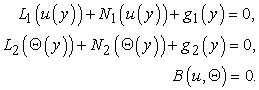 | (10) |
where 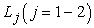 , are linear operator,
, are linear operator, 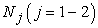 are non-linear operator,
are non-linear operator, 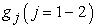 are known function and B is a boundary operator.By means of OHAM we first construct an optimal homotopy
are known function and B is a boundary operator.By means of OHAM we first construct an optimal homotopy 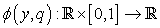 which satisfies the following equations:
which satisfies the following equations: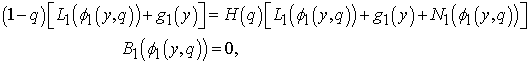 | (11) |
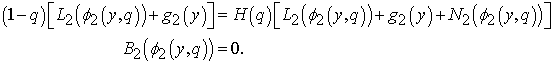 | (12) |
where 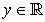 and
and 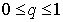 is an embedding parameter,
is an embedding parameter, 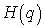 is a nonzero auxiliary function for
is a nonzero auxiliary function for 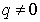 and
and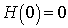 , and
, and 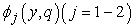 are unknown functions. Clearly, when
are unknown functions. Clearly, when 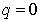 and
and 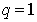 it holds that
it holds that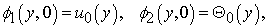 | (13) |
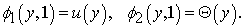 | (14) |
Choose the auxiliary function 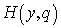 in the form
in the form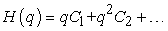 | (15) |
where 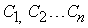 are constants to be determined. Construct a Taylor's series solution of equations
are constants to be determined. Construct a Taylor's series solution of equations 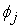 in the form
in the form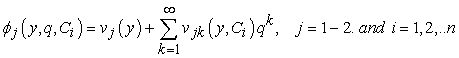 | (16) |
where  represent
represent  and
and 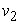 represent
represent  . Substituting Eq. (16) into Eqs. (11) - (14) and collecting the same powers of q, and equating each coefficient of q to zero, we obtain
. Substituting Eq. (16) into Eqs. (11) - (14) and collecting the same powers of q, and equating each coefficient of q to zero, we obtain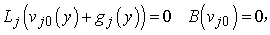 | (17) |
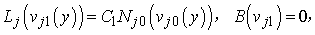 | (18) |
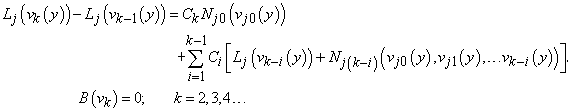 | (19) |
where 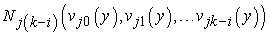 is the coefficient of
is the coefficient of 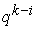 , obtained by expanding
, obtained by expanding 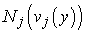 in series with respect to the embedding parameter
in series with respect to the embedding parameter 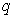 .
.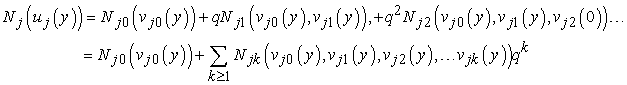 | (20) |
The solution of equations (31) and (32) can be approximately obtained in the form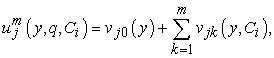 | (21) |
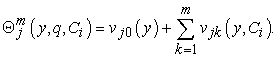 | (22) |
The residual 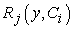 follows as
follows as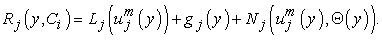 | (23) |
If 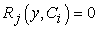 , then
, then 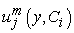 will be the exact solution. Generally such a case will not happen for nonlinear problems, but we can minimize the functional by the method of lease squares
will be the exact solution. Generally such a case will not happen for nonlinear problems, but we can minimize the functional by the method of lease squares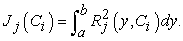 | (24) |
where 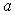 and
and 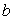 belong to the domain of the problem. Finally, the unknown constants
belong to the domain of the problem. Finally, the unknown constants 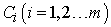 can be optimally identified from the conditions
can be optimally identified from the conditions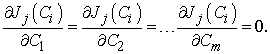 | (25) |
with these known values of 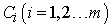 , the approximate solutions are well determined.
, the approximate solutions are well determined.
4. Solutions for Velocity and Temperature
Choosing the linear and nonlinear operators defined by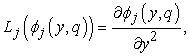 | (26) |
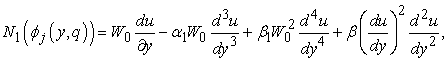 | (27) |
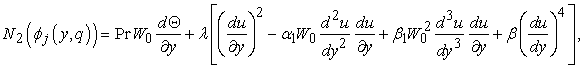 | (28) |
The correspond boundary conditions are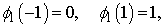 | (29) |
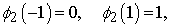 | (30) |
The zeroth order deformation: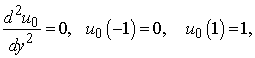 | (31) |
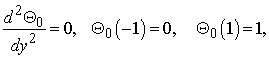 | (32) |
The first order deformation: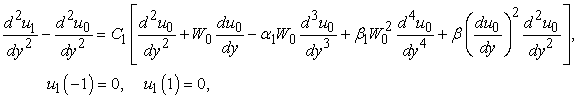 | (33) |
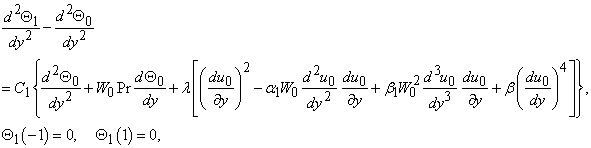 | (34) |
The second order deformation: | (35) |
 | (36) |
By using the widely applied symbolic computational software MATHEMATICA. It is found that the solutions of Eqs. (31) - (36) are: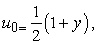 | (37) |
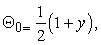 | (38) |
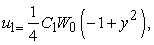 | (39) |
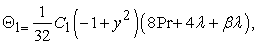 | (40) |
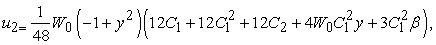 | (41) |
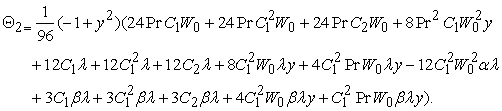 | (42) |
In view of Eq. (41), the second order approximation solution  for equations (15) and (16):
for equations (15) and (16):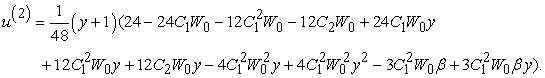 | (43) |
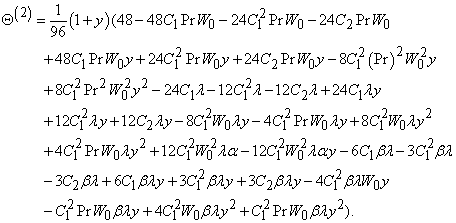 | (44) |
Using Eq. (3), these result into the following residual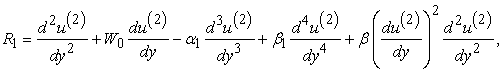 | (45) |
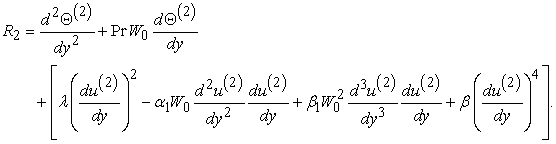 | (46) |
and the functional 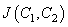 is defined as
is defined as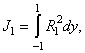 | (47) |
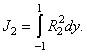 | (48) |
The unknown constant 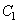 and
and 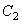 can be calculated from the conditions
can be calculated from the conditions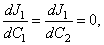 | (49) |
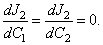 | (50) |
The unknown constant 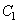 and
and 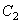 can be calculated from the conditions
can be calculated from the conditions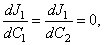 | (51) |
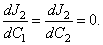 | (52) |
(a) For fluid velocity, we take α = 0.5. Using the condition (25), we obtain the values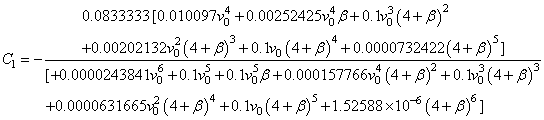 | (53) |
and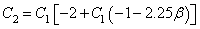 | (54) |
For no transpiration rate, 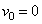 , therefore from Eq. (43) ; the approximate solution of second order is found to be
, therefore from Eq. (43) ; the approximate solution of second order is found to be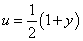 | (55) |
The above mentioned expression is of the same type that was obtained by Siddiqui et al.[5] :For transpiration rate 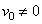 . Therefore as a particular case, taking suction (
. Therefore as a particular case, taking suction (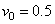 ) and
) and 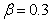 , we obtain
, we obtain 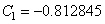 ,
, 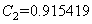 and the approximate analytical solution as
and the approximate analytical solution as | (56) |
For injection case (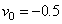 ) and
) and 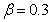 we obtain
we obtain  | (57) |
The general form is given by | (58) |
(b) For fluid temperatureTaking the values 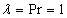 ,
, 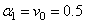 , we obtained
, we obtained 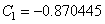 ,
, 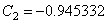 , and the approximate solution of second order, in the form
, and the approximate solution of second order, in the form 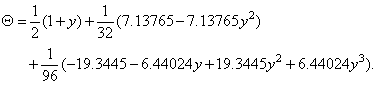 | (59) |
and the general form | (60) |
5. Analysis of Results
Fig. 1 shows the comparison between the present results, obtained by using OHAM and those Siddiqui et al. [5] obtained by employing HPM in non-porous media. We note that, the precision from the solution acquired through the current method, for velocity and temperature pro.les are excellent.Fig. 2(a) shows the effect of the material constant β on temperature profile, in case of of suction, when 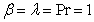 and
and 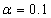 . It is observed from this figure that the fluid temperature increases with increase in the value of β. From Fig. 2 (b), for injection case, it is observed that the behavior of the temperature profile is slow to that in Fig. 2 (a).Fig. 3 (a) shows the effect of the material constant β for velocity profile in case of suction, when
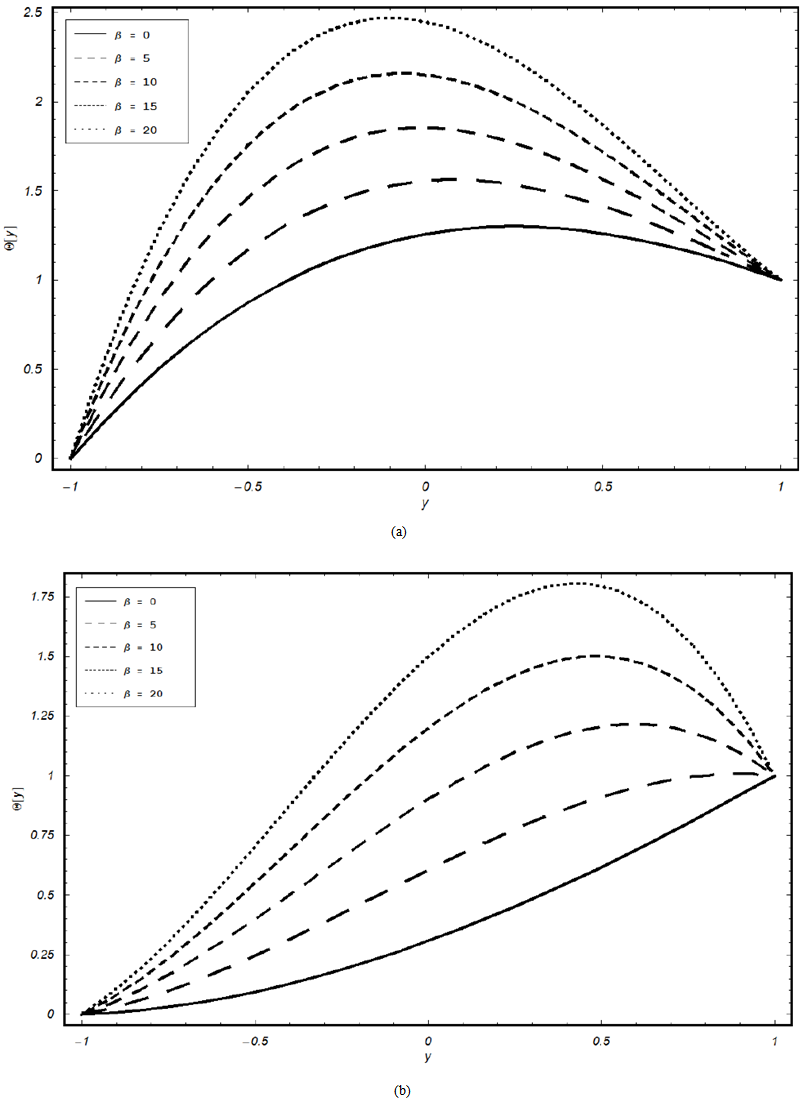
. It is observed from this figure that the fluid temperature increases with increase in the value of β. From Fig. 2 (b), for injection case, it is observed that the behavior of the temperature profile is slow to that in Fig. 2 (a).Fig. 3 (a) shows the effect of the material constant β for velocity profile in case of suction, when 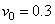 is fixed. It is observed from this figure that the fluid velocity decreases with increase in the value of β. However, in Fig. 3 (b) for injection case, the behavior of the velocity profile is reversed to that in Fig. 3 (a).
is fixed. It is observed from this figure that the fluid velocity decreases with increase in the value of β. However, in Fig. 3 (b) for injection case, the behavior of the velocity profile is reversed to that in Fig. 3 (a).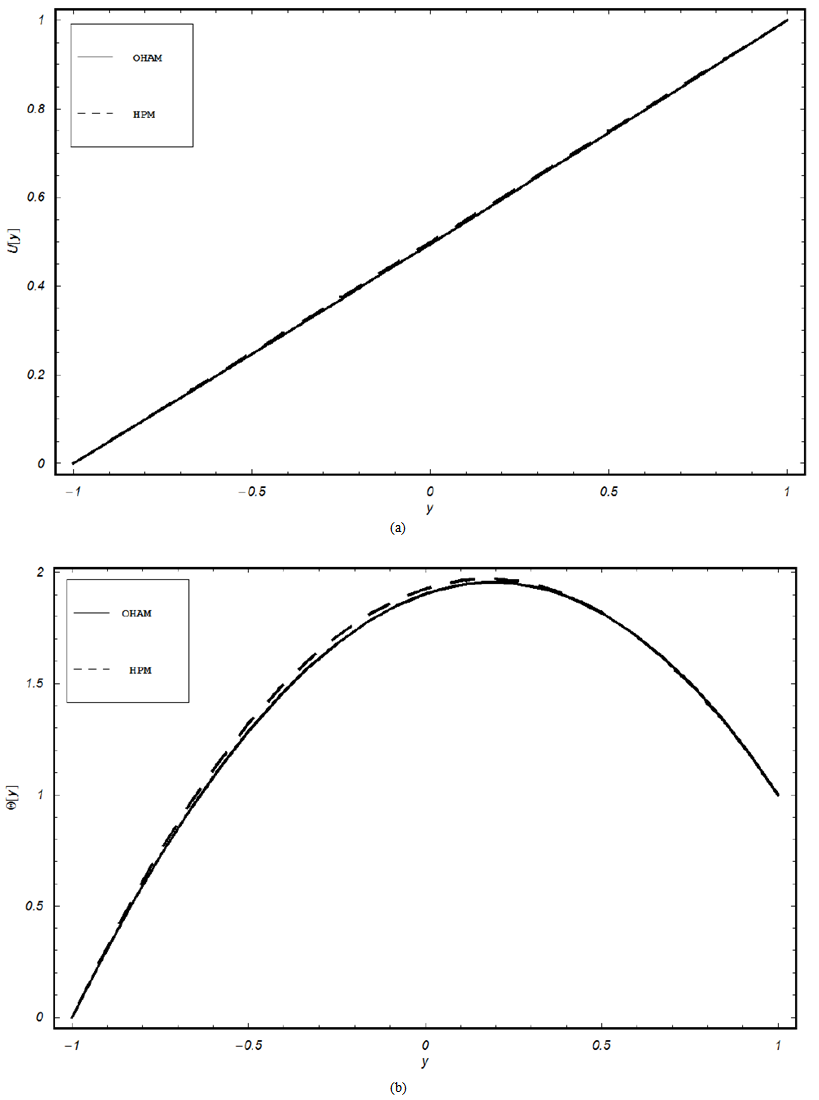 | Figure 1. Comparison between the results obtained from OHAMand Siddiqui et al. results [5] obtained from HPM in case (a) velocity and case (b) temperature when 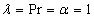 and and 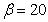 |
 | Figure 2. Effect of material constant β on the temperature profiles for the case of suction (a) and injection (b) when 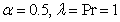 and and 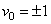 |
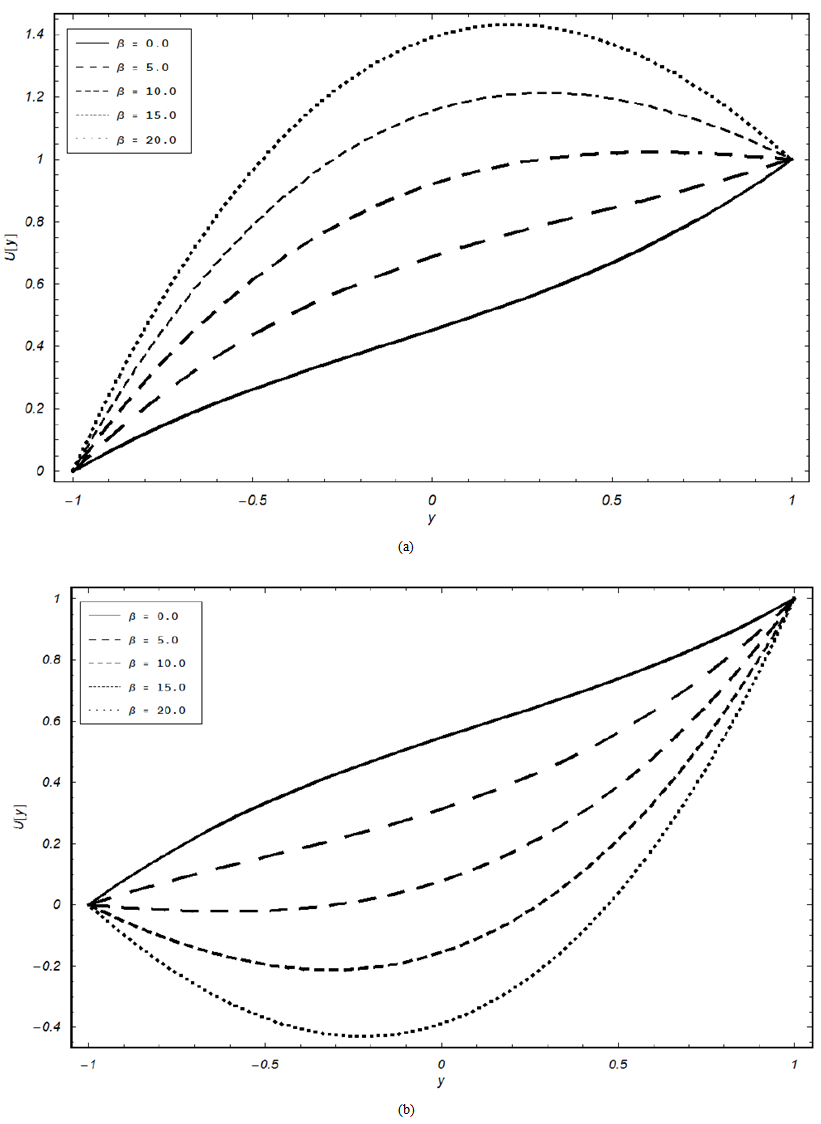 | Figure 3. Effect of material parameter β on the velocity pro.les for the case of suction (a) and injection (b) when 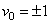 |
6. Conclusions
Analytical explicit expressions for the velocity and temperature profiles have been obtained for the Couette flow of a third grade fluid between two parallel porous plates, which match well with the previous analytical solutions the HPM solutions [5]. It is found that the Couette flow features dominate as viscoelastic parameter is increased. It is also observed that the effects of the fluid/temperature injection or suction exert a great influence on the general flow pattern, by enhancing or suppressing the influence of the wall into the flow domain.
References
| [1] | S. Okoya Samuel, Disappearance of criticality for reaction third-grade fluid with Reynold's model viscosity in a fiat channel International Journal of Non-Linear Mechanics, 46 (2011) 1110-1115. |
| [2] | S. Abelman, E. Momoniat and T. Hayat, Couette fiow of a third grade fiuid with rotating frame and slip condition, Nonlinear analysis: Real world applications 10 (2009) 3329-3334. |
| [3] | T. Hayat, S. Hina, A. Awatif and S. Asghar. Effect of wall properties on the peristaltic flow of a third grade fluid in a curved channel with heat and mass transfer, International Journal of Heat and mass transfer 54 (2011) 5126-5136. |
| [4] | D. Mohammad, K. Shashi and K. Surendra, Exact analytical solutions for Poiseuille and Couette-Poiseuille flow of third grade fluid between parallel plates, Communication Nonlinear Science Numerical Simulation 17 (2012) 1089-1097. |
| [5] | A. M. Siddiqui, A. Zeb, Q. K. Ghori and A. M Benharbit, Homotopy analysis method for heat transfer flow of a third grade fluid between parallel plates, Chaos, Solitons and Fractals 36 (2008)182-192. |
| [6] | G. Adomian, Solving frontier problems of physics: the decomposition method. Boston: Kluwer Academic; 1994. |
| [7] | J. H. He, Variational iterative method- a kind of non-linear analytical technique: some examples. International Journal of Non-Linear Mechanics 34 (1999) 699-708. |
| [8] | M. Javidi, A numerical solution of the generalized Burgers-Huxley equation by spectral collocation method. Applied Mathematics and Computation 178 (2006) 338-344. |
| [9] | L. Shijun, Notes on the homotopy analysis method: Some definitions and theorems 14 (2009) 983-997. |
| [10] | J.H. He, The homotopy perturbation method for nonlinear oscillators with discontinuities, Applied Mathematics and Computation 151 (2004) 287-292. |
| [11] | V. Marinca, and N. Herisanu, Application of Optimal Homotopy Asymptotic Method for Solving Nonlinear Equations Arising in Heat Transfer, International Communications in Heat and Mass Transfer 35 (2008) 710-715. |

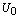 and the effect constant pressure gradient is neglected. The movement of fluid is solely due to motion of the upper plate. The fluid is brought into motion through the action of viscous stress at the plate. The temperature of the lower plate is maintained at
and the effect constant pressure gradient is neglected. The movement of fluid is solely due to motion of the upper plate. The fluid is brought into motion through the action of viscous stress at the plate. The temperature of the lower plate is maintained at 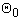 and that of the upper plate at
and that of the upper plate at 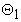 . Mathematical model of the present flow problem are formulated as below:
. Mathematical model of the present flow problem are formulated as below: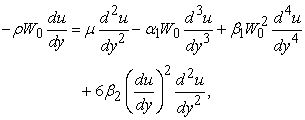
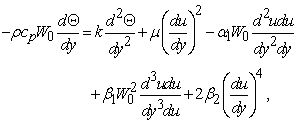
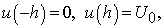
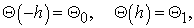
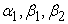 are the material moduli,
are the material moduli, 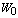 is the sunction/injection parameter,
is the sunction/injection parameter, 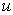 fluid velocity,
fluid velocity, 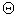 is the fluid temperature,
is the fluid temperature, 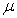 is the fluid viscosity,
is the fluid viscosity, 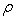 is the fluid density,
is the fluid density, 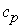 is the specific heat capicity and
is the specific heat capicity and 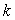 is the thermal conductivity.Introducing the dimensionless parameters
is the thermal conductivity.Introducing the dimensionless parameters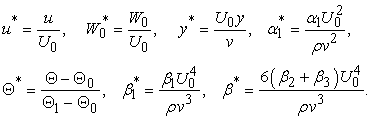
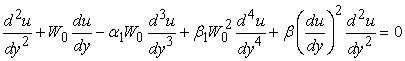
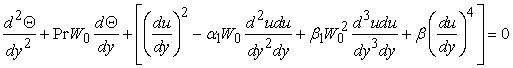

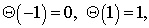
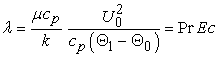 , Pr is the Prandtl number, Ec is the Eckert number and λ is the Brinkman number.
, Pr is the Prandtl number, Ec is the Eckert number and λ is the Brinkman number.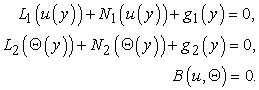
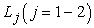 , are linear operator,
, are linear operator, 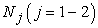 are non-linear operator,
are non-linear operator, 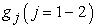 are known function and B is a boundary operator.By means of OHAM we first construct an optimal homotopy
are known function and B is a boundary operator.By means of OHAM we first construct an optimal homotopy 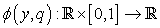 which satisfies the following equations:
which satisfies the following equations: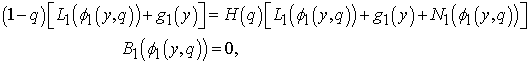
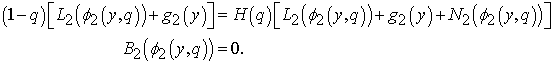
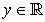 and
and 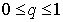 is an embedding parameter,
is an embedding parameter, 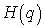 is a nonzero auxiliary function for
is a nonzero auxiliary function for 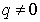 and
and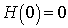 , and
, and 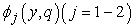 are unknown functions. Clearly, when
are unknown functions. Clearly, when 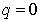 and
and 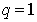 it holds that
it holds that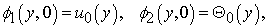
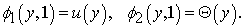
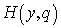 in the form
in the form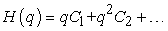
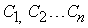 are constants to be determined. Construct a Taylor's series solution of equations
are constants to be determined. Construct a Taylor's series solution of equations 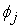 in the form
in the form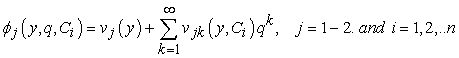
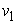 represent
represent 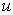 and
and 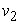 represent
represent 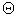 . Substituting Eq. (16) into Eqs. (11) - (14) and collecting the same powers of q, and equating each coefficient of q to zero, we obtain
. Substituting Eq. (16) into Eqs. (11) - (14) and collecting the same powers of q, and equating each coefficient of q to zero, we obtain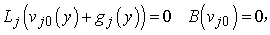
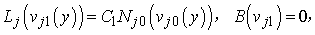
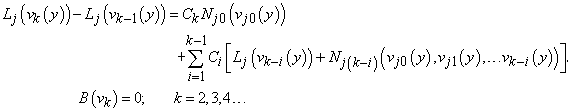
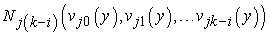 is the coefficient of
is the coefficient of 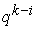 , obtained by expanding
, obtained by expanding 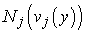 in series with respect to the embedding parameter
in series with respect to the embedding parameter 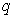 .
.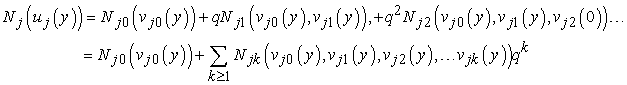
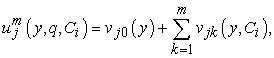
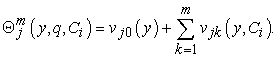
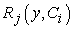 follows as
follows as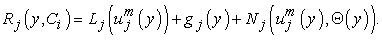
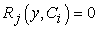 , then
, then 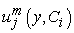 will be the exact solution. Generally such a case will not happen for nonlinear problems, but we can minimize the functional by the method of lease squares
will be the exact solution. Generally such a case will not happen for nonlinear problems, but we can minimize the functional by the method of lease squares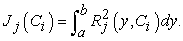
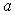 and
and 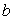 belong to the domain of the problem. Finally, the unknown constants
belong to the domain of the problem. Finally, the unknown constants 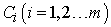 can be optimally identified from the conditions
can be optimally identified from the conditions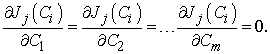
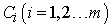 , the approximate solutions are well determined.
, the approximate solutions are well determined.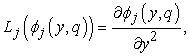
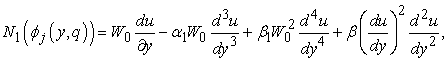
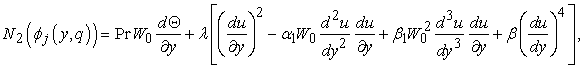
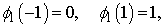
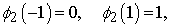
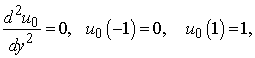
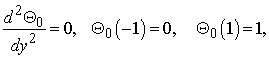
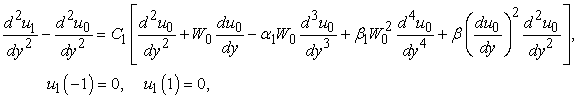
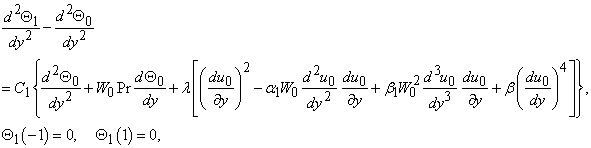


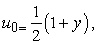
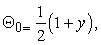
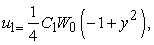
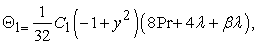
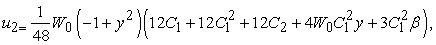
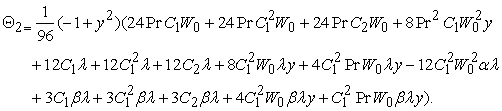
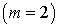 for equations (15) and (16):
for equations (15) and (16):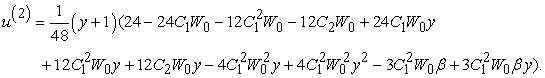
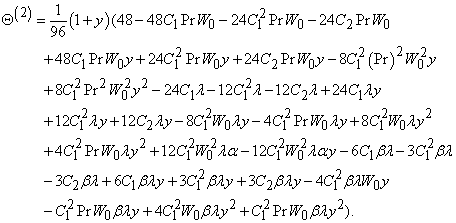
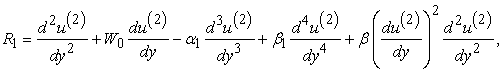
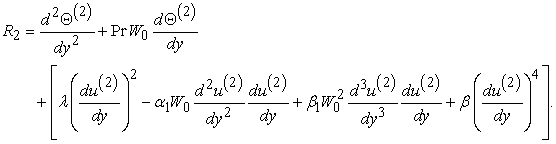
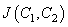 is defined as
is defined as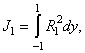
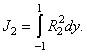
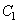 and
and 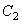 can be calculated from the conditions
can be calculated from the conditions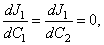
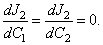
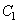 and
and 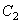 can be calculated from the conditions
can be calculated from the conditions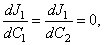
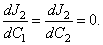
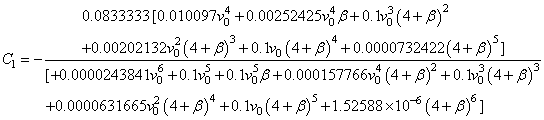
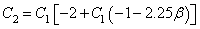
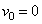 , therefore from Eq. (43) ; the approximate solution of second order is found to be
, therefore from Eq. (43) ; the approximate solution of second order is found to be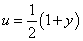
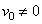 . Therefore as a particular case, taking suction (
. Therefore as a particular case, taking suction (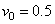 ) and
) and 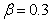 , we obtain
, we obtain 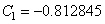 ,
, 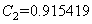 and the approximate analytical solution as
and the approximate analytical solution as
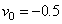 ) and
) and 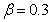 we obtain
we obtain 

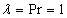 ,
, 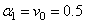 , we obtained
, we obtained 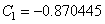 ,
, 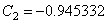 , and the approximate solution of second order, in the form
, and the approximate solution of second order, in the form 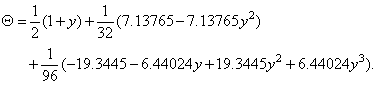

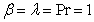 and
and 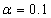 . It is observed from this figure that the fluid temperature increases with increase in the value of β. From Fig. 2 (b), for injection case, it is observed that the behavior of the temperature profile is slow to that in Fig. 2 (a).Fig. 3 (a) shows the effect of the material constant β for velocity profile in case of suction, when
. It is observed from this figure that the fluid temperature increases with increase in the value of β. From Fig. 2 (b), for injection case, it is observed that the behavior of the temperature profile is slow to that in Fig. 2 (a).Fig. 3 (a) shows the effect of the material constant β for velocity profile in case of suction, when 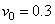 is fixed. It is observed from this figure that the fluid velocity decreases with increase in the value of β. However, in Fig. 3 (b) for injection case, the behavior of the velocity profile is reversed to that in Fig. 3 (a).
is fixed. It is observed from this figure that the fluid velocity decreases with increase in the value of β. However, in Fig. 3 (b) for injection case, the behavior of the velocity profile is reversed to that in Fig. 3 (a).
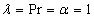 and
and 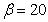

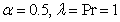 and
and 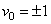

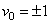
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML