| [1] | Ajie, I. J., Onumanyi P., and Ikhile, M. N. O., (2011) Journal of The Nigerian Mathematical Society, vol. 13, p. 6-9. |
| [2] | Akinfenwa, O., Yao N. and Jator, S., (2011) ‘Implicit two step continuous hybrid block methods withfour Off-Steps point for solving stiff ordinary differential equation.’ In Proceedings of the International Conference on Computational and Applied Mathematics, Bangkok, Thailand, p. 425-428. |
| [3] | Akinfenwa, O., Yao, N. and Jator, S., (2011) “A Self-Starting Block Adams Mathods for Solving Stiff Ordinary Differential Equation,” in Computational Science and Engineering (CSE), 2011 IEEE 14thInternational Conference, p. 127-136. |
| [4] | Amodio, P. (1996) A-stable k-step Linear Multistep Formulae of Order 2k for the Solution of StiffODEs, Report 24/96 Dipartimento di Matematica, Universita' degliStudi di Bari. |
| [5] | Bond, I. and Cash, J., (1979) ‘A Block Method for Numerical Integration of Stiff systems of ODEs.’BIT, vol. 19, no. 2, p. 429-447. |
| [6] | Brugnano, L. and Magherini, C. (2000), Blended implementation of block implicit methods for ordinary differential equations, Appl. Numer Math. 42, 29-45. |
| [7] | Brugnano, L. and Magherini, C. (2007), Blended implicit methods for solving ordinary differential equations and delay algebraic problems and their extention for second order problems, J. Comput. Appl. Math. 205, 777-790. |
| [8] | Brugnano, L. and Trigiante, D., (2001) Block Implicit Methods for ODEs in: D. Trigiante (Ed). Recen Tends in Numerical Analysis, New York: Nova Science Publ. Inc.. |
| [9] | Brugnano, L. and Trigiante, D. (1998), Solving differential problems bymultistep initial and boundary value methods. Published by Gordon and BeachScience Publishers. |
| [10] | Brugnano, L. and Trigiante, D. (1997), Boundary Value Methods for the approximation ordinary differential equations, Lecture notes in comput. Sci. 1196, 78-89. |
| [11] | Cash, J. and Diamantakis, M., (1994) “On The Implementation of Block Runge-Kutta Methods for Stiff ivps,” Ann Numer. Math., vol. 1, no. 2, p. 385-398. |
| [12] | Charter, P. (1994) ‘L-stableparallelone-blockmethodsfor Ordinary differential equations’ SIAM J. numer.anal.Vol. 31, No. 2, pp. 552-571. |
| [13] | Curtiss, C. F. and Hirshfelder, J. O. (1952) Integration of stiff equations, Proc. Nat. Acad. Sci. U.S.A. 38 p. 235-243 |
| [14] | Dahlquist, G., (1956) “Convergence and stability in the numerical integration of ordinary differential equations, Math. Scand. 4, p. 33-53. |
| [15] | Fatunla, S. O., (1991) “Block Method for Second Order IVPs” J. Compt. Maths, vol. 41, p. 55-63. |
| [16] | Fatunla, S.O. (1994), Parallel methods for second order ordinary differential equations. Proceedings of the International Conference on Computational Mathematics, University of Ibadan Press, pp 87-99. |
| [17] | Henrici, P., (1962) Discrete Variable Methods ODEs. New York: John Wiley. Journal of The Nigerian Mathematical Society, vol. 12. |
| [18] | Muka, K.O. and Ikhile, M.N.O. (2012), Parallel multi-derivative backward differentiation type block II methods for stiff ODEs. 417–434. |
| [19] | Onumanyi, P., Awoyemi, D. O., Jator, S. N. and Sirisena, U. W., (1994) ‘‘New Linear Multistep Methods with Continuous Coefficients for First Order IVPs” Journal of The Nigerian Mathematical Society, vol. 13. |
| [20] | Onumanyi, P., Sirisena, W.U. and Chollom, J. P., (2001) Continuous hybrid methods through multistep collocation. Abacus, Journal Mathematical Association of Nigeriapp 58-64. |
| [21] | Shampine, L. and Watts, H. A., (1972) “A-Stable Block One-Step Methods,” BIT, vol. 23, p. 252-266. |
| [22] | Sparrow, C. (982) The Lorenz Equations: Bifurcations, Chaos, and Strange Attractors, Springer-Verlag, New York, 1. |
| [23] | Zanariah, M. and Suleiman, M., (2007) ‘Implementation of Four-Point Fully Implicit Block Method for Solving Ordinary Differential Equation,’ Applied Maths and Comp., vol 184, p.513-522. |

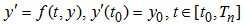
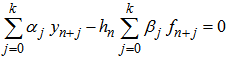
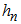 is the variable step size,
is the variable step size, 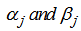 ,
, 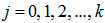 are coefficients which can be uniquely determined.By introducing two polynomials
are coefficients which can be uniquely determined.By introducing two polynomials 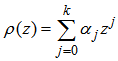 ,
, 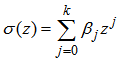 (2.1) can be rewritten as
(2.1) can be rewritten as 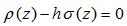
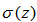 in its simplest form,
in its simplest form, 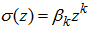 we obtain a class of order k,k-step LMF known as BDF and are given by
we obtain a class of order k,k-step LMF known as BDF and are given by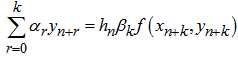
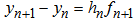 . which is the only L-stable member of the BDF family known of order one. It is in fact known that BDF of order
. which is the only L-stable member of the BDF family known of order one. It is in fact known that BDF of order 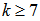 are zero unstable hence will not converge. Cases of k=4, 5 and 6 will be used in our constructions.Almost all the families of linear multistep methods are obtained by imposing one restriction or the other on the structure of the polynomials
are zero unstable hence will not converge. Cases of k=4, 5 and 6 will be used in our constructions.Almost all the families of linear multistep methods are obtained by imposing one restriction or the other on the structure of the polynomials 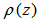 or
or 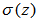 . The family constructed without ‘a priori’ restrictions on such polynomials by imposing maximum order on (2.1) in order to get the coefficients
. The family constructed without ‘a priori’ restrictions on such polynomials by imposing maximum order on (2.1) in order to get the coefficients 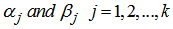 is called TOMs. This familywas considered by Dahlquist (1956) and presented as unstable methods. Exampleis the Sixth Order TOM below which we will use in constructing our family of methods.
is called TOMs. This familywas considered by Dahlquist (1956) and presented as unstable methods. Exampleis the Sixth Order TOM below which we will use in constructing our family of methods.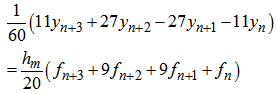
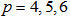 where p is theorder. These are obtained by pairing TOMs with k = 3, order p = 2k and the BDF with
where p is theorder. These are obtained by pairing TOMs with k = 3, order p = 2k and the BDF with 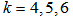 each of order k.The pairs are then shifted forwards imultaneously repeatedly
each of order k.The pairs are then shifted forwards imultaneously repeatedly 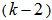 timesto give a set of 2(k - 1) equations which can be solved to obtain the unknowns
timesto give a set of 2(k - 1) equations which can be solved to obtain the unknowns 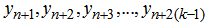 . For values of
. For values of 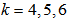 , the construction yields the new one step block method of the form
, the construction yields the new one step block method of the form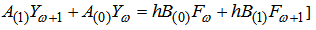
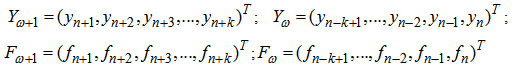
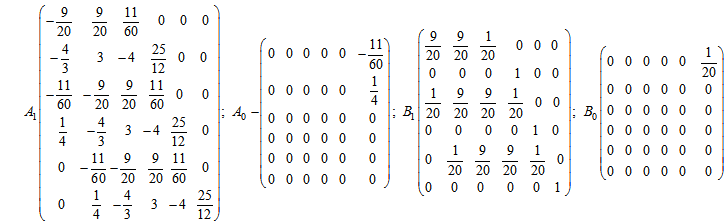 Case k = 5
Case k = 5
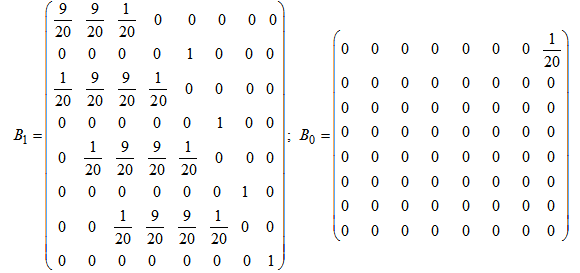 Case k = 6
Case k = 6
 We have constructed the one-step block LMF of order
We have constructed the one-step block LMF of order  in this section using only a pair of LMF. The problem of looking for additional methods to form blocks are overcome.
in this section using only a pair of LMF. The problem of looking for additional methods to form blocks are overcome.
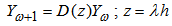
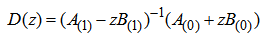
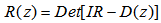
 identity matrix. The stability domain S of a one-step block method is
identity matrix. The stability domain S of a one-step block method is 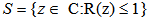
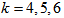 which satisfies (3.5).k = 4
which satisfies (3.5).k = 4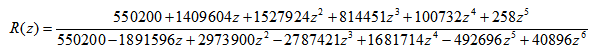 k = 5
k = 5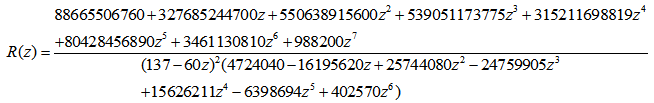 k = 6
k = 6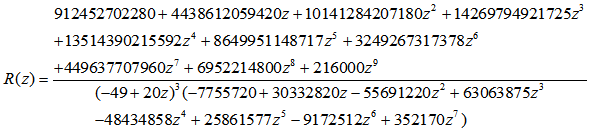 The boundary locus plots of the stability domain for k= 4, 5, and 6 are given as follows:
The boundary locus plots of the stability domain for k= 4, 5, and 6 are given as follows: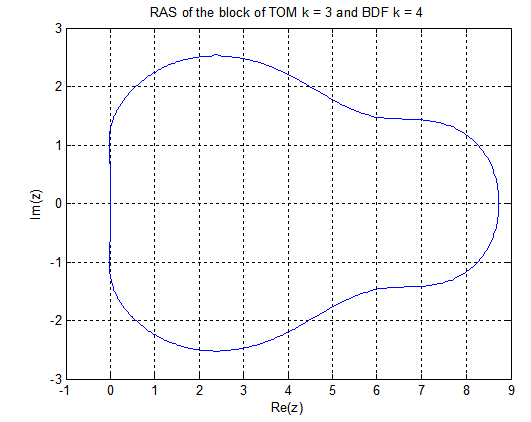
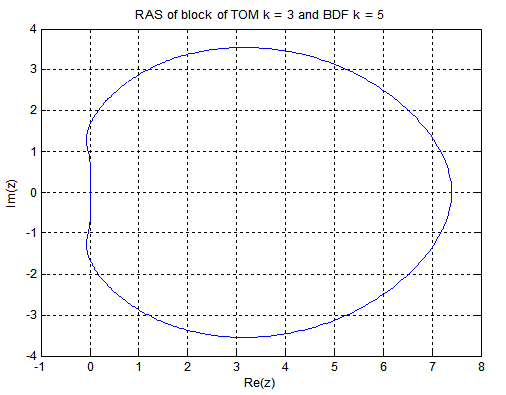
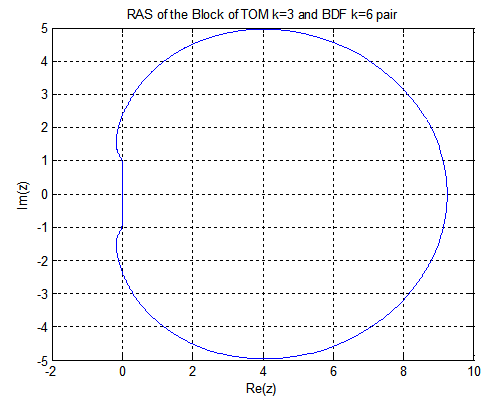
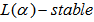 since
since 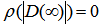 . (see Chartier (1993))
. (see Chartier (1993))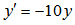 is solved with h = 0.01 using the three methods, order 4, 5 and 6 and the results displayed in the table below
is solved with h = 0.01 using the three methods, order 4, 5 and 6 and the results displayed in the table below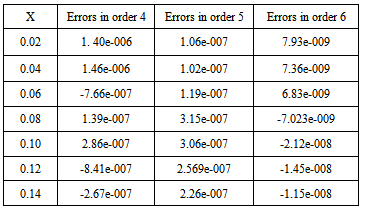 It can easily be seen that the accuracy increases as the order increases.Example 4.2 Lorenz chaotic attractor (see Sparrow (1982))
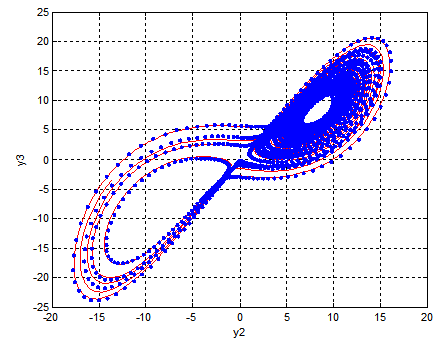
It can easily be seen that the accuracy increases as the order increases.Example 4.2 Lorenz chaotic attractor (see Sparrow (1982))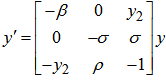 ;
; 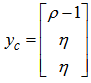 ;
; 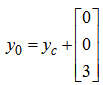
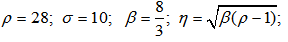
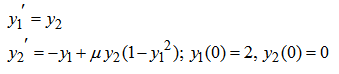
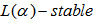 block methods that is self-starting has been introduced. They combine the accuracy of TOMs and the stability properties of BDFs in the block implicit pairs formed for adequate block-by-block forward integration. The analysis of the stability properties shows that the methods are
block methods that is self-starting has been introduced. They combine the accuracy of TOMs and the stability properties of BDFs in the block implicit pairs formed for adequate block-by-block forward integration. The analysis of the stability properties shows that the methods are 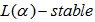 for
for 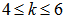 . The numerical experiments considered showed that the methods are comparable to existing ones.
. The numerical experiments considered showed that the methods are comparable to existing ones. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML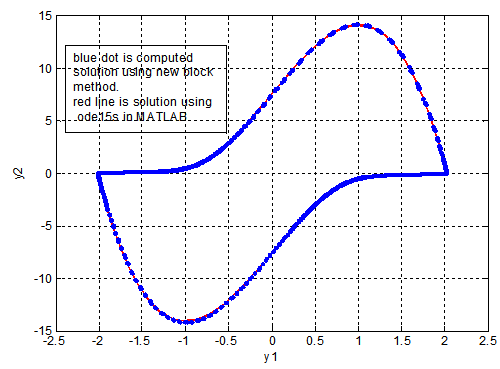
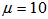 , using order 6 of our method and step size h = 0.01. The result is displayed in the figure below
, using order 6 of our method and step size h = 0.01. The result is displayed in the figure below