Kateryna V. Nesvit
Department of Mathematical Physics and Computational Mathematics, Karazin Kharkiv National University, Kharkov, 61022, Ukraine
Correspondence to: Kateryna V. Nesvit, Department of Mathematical Physics and Computational Mathematics, Karazin Kharkiv National University, Kharkov, 61022, Ukraine.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
In this paper a diffraction problem of a plane E-polarized wave on screened pre-Cantor grating is considered. A discrete mathematical model of this diffraction problem has been developed with the help of the specific quadrature formulas with the nodes in the nulls of Chebyshev polynomials. Using the parametric representations of hypersingular integral operator and integral operator with logarithmic singularity in the kernel, a hypersingular integral equation has been proposed. Besides, an effective discrete singularities method which has been applied to the numerical experiment of developed mathematical model has been proved to be one of the most efficient ways to solve such type of diffraction problems.
Keywords:
Hypersingular integral equation, Diffraction problem, Electromagnetic fields
Cite this paper: Kateryna V. Nesvit, Scattering of TE Wave on Screened Pre-Cantor Grating Based on Hypersingular Integral Equations, American Journal of Computational and Applied Mathematics , Vol. 4 No. 1, 2014, pp. 9-16. doi: 10.5923/j.ajcam.20140401.02.
1. Introduction
A transverse mode of a beam of electromagnetic radiation is perpendicular to the propagation direction of the beam. Transverse modes can be classified into two types: the transverse electric and transverse magnetic modes. If there is no magnetic field in the propagation direction then this is considered to be the TM case, while when there is no electric field in the direction of propagation then this is the TE case. In this paper the TE wave case is considered (see Fig. 1).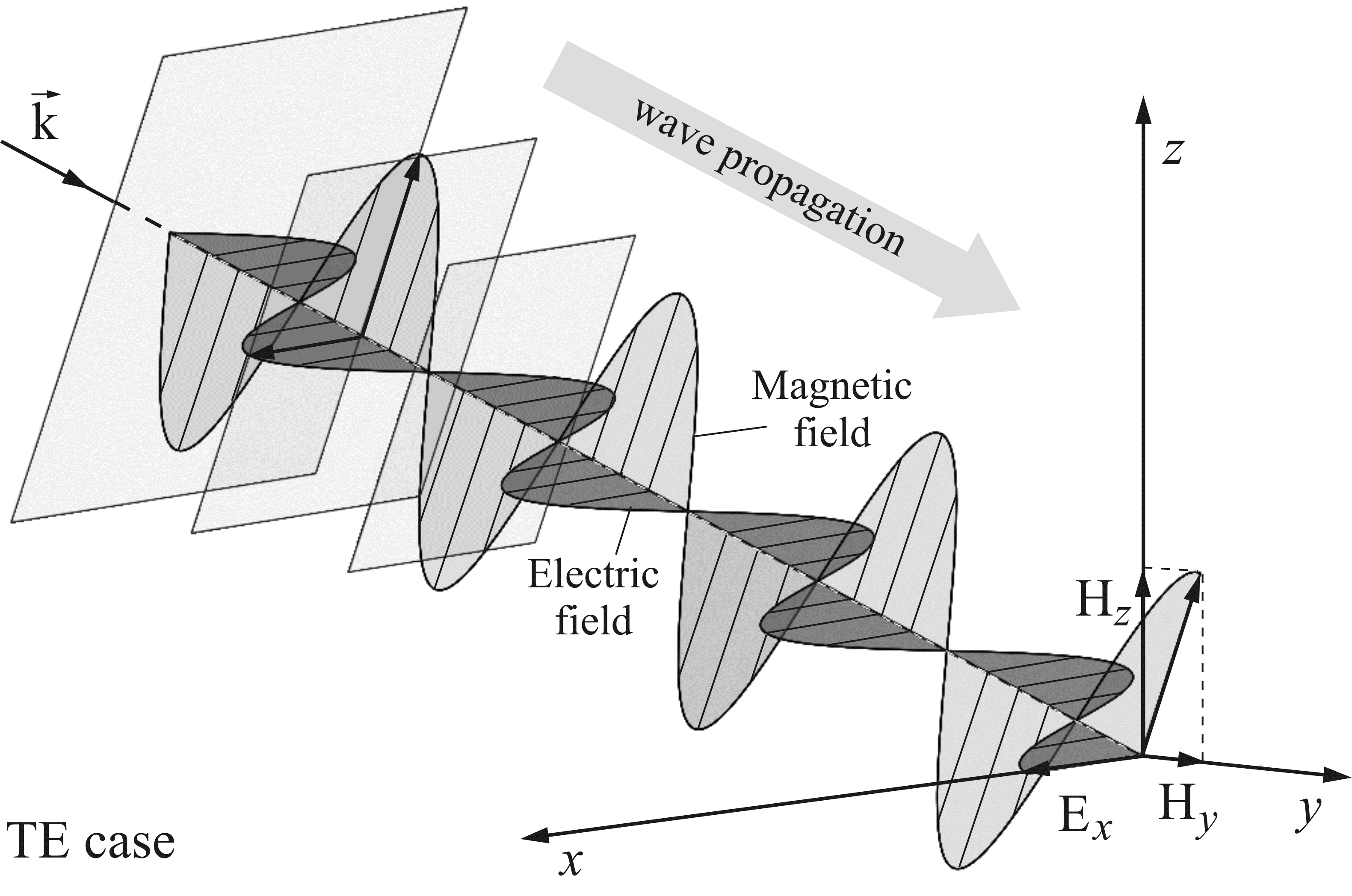 | Figure 1. Propagation of the plane electromagnetic wave in TE case |
Mathematical modelling of the interaction of electromagnetic radiation with plane-parallelelectrodynamic structures is considered in many papers related to the solution of applied problems. These structures include pre-Cantor perfectly conducting gratings above flat screen reflector. The key literature in this particular scientific field is formed by a monograph[1] and articles[2],[3], where boundary-value problems of diffraction mathematics theory are solved by considering boundary singular and hypersingular integral equations. In article[4] a mathematical and a discrete mathematical models of the diffraction problem on screened pre-Cantor grating for the case of H-polarization have been presented. Furthermore, a numerical experiment has been performance with the help of efficient discrete singularities method (DSM). In[5] a mathematical model of this diffraction problem was carried out.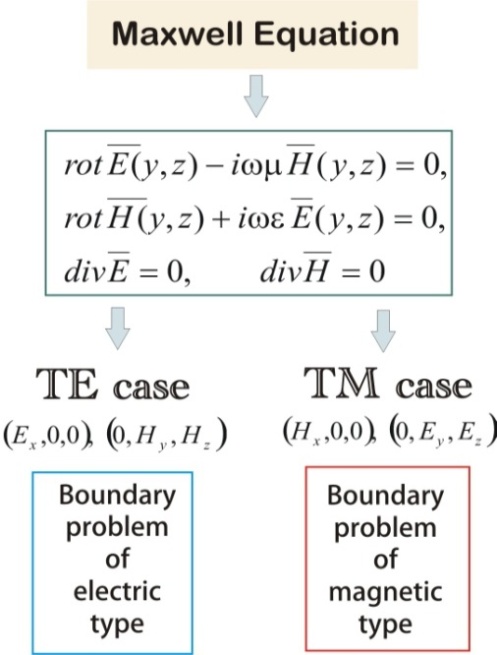 | Figure 2. Schematic structure to solve of 2D diffraction problem |
 | Figure 3. Constructing a pre-Cantor grating of the five order |
The overall aim of this article is to develop a discrete mathematical model of hypersingular integral equations (HSIEs) using of the specific quadrature formulas with the nodes in the nulls of Chebyshev polynomials.Novelty of this work is to choose the special strips in the form of pre-Cantor strips[11] for considering TE wave diffraction problem.
2. TE Diffraction Problem
To solve a two-dimensional (2-D) scattering problem, the total field which satisfies Maxwell’s equations (see Fig. 2), boundary conditions on the strips and flat screen reflector, the Sommerfeld radiation conditions and the Meixner edge condition has been calculated.Let us define the sets of pre-Cantor[11] intervals which are obtained by constructing a Cantor set on the N-th step - Fig. 3.We consider the TE wave diffraction problem on multiple slits with finite numbers of non-equidistant strips where beginning and end of the strips are given by formula (1). Considering that the pre-Cantor strips are perfect electrically conducting (PEC). Propagation direction of a plane wave is given by direction of the wave vector 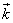 (see Fig. 4).Cartesian coordinate system is chosen so that the set of the strips is located in XY plane, and the X axis is parallel to the strips’ edges (see Fig. 4).
(see Fig. 4).Cartesian coordinate system is chosen so that the set of the strips is located in XY plane, and the X axis is parallel to the strips’ edges (see Fig. 4).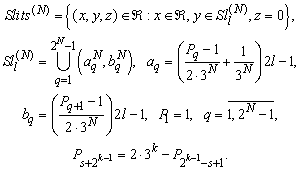 | (1) |
The time factor is assumed as 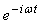 and omitted.The unique non-zero independent component of the electric field satisfies the two-dimensional Helmholtz equation above the flat screen reflector and without the strips:
and omitted.The unique non-zero independent component of the electric field satisfies the two-dimensional Helmholtz equation above the flat screen reflector and without the strips: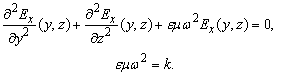 | (2) |
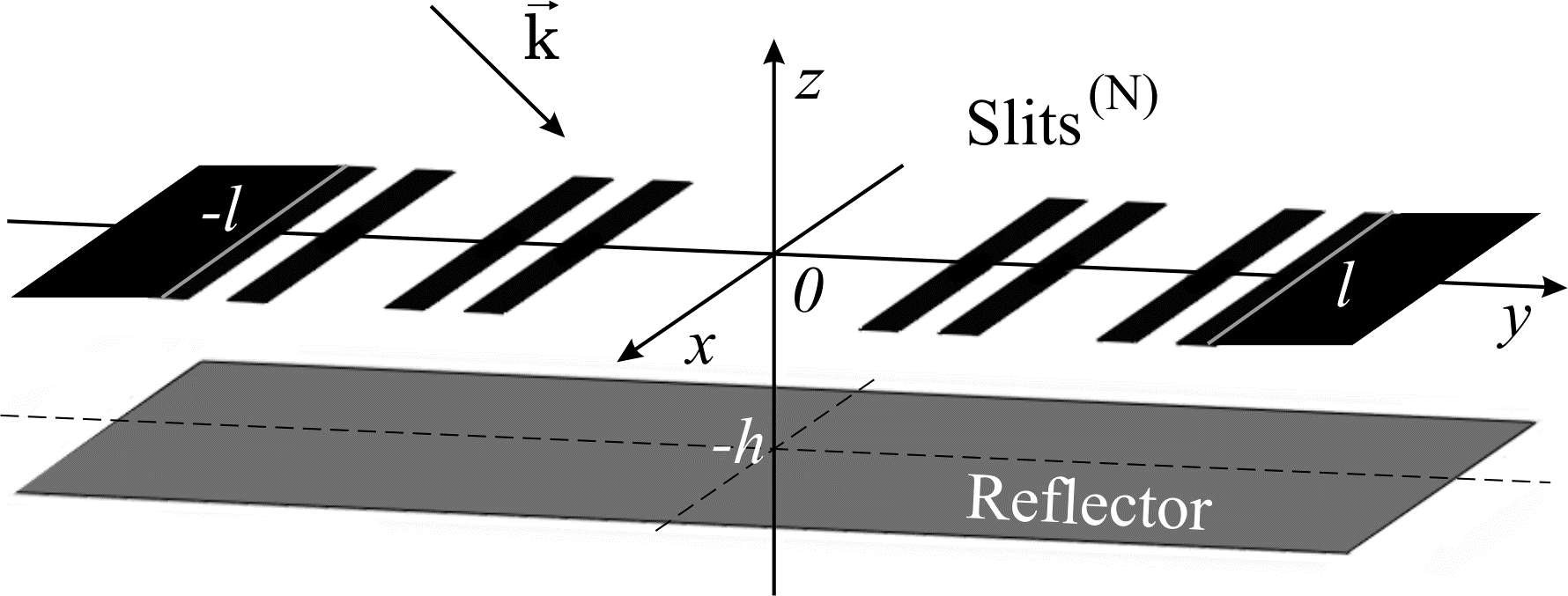 | Figure 4. Schematic of the considered diffraction structure |
Besides, this component satisfies all the aforementioned conditions and the unique non-zero independent components of the magnetic field are represented by Maxwell’s equations: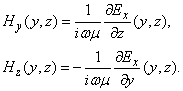 | (3) |
For further convenience, the dimensionless coordinates are considered.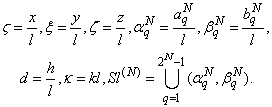 | (4) |
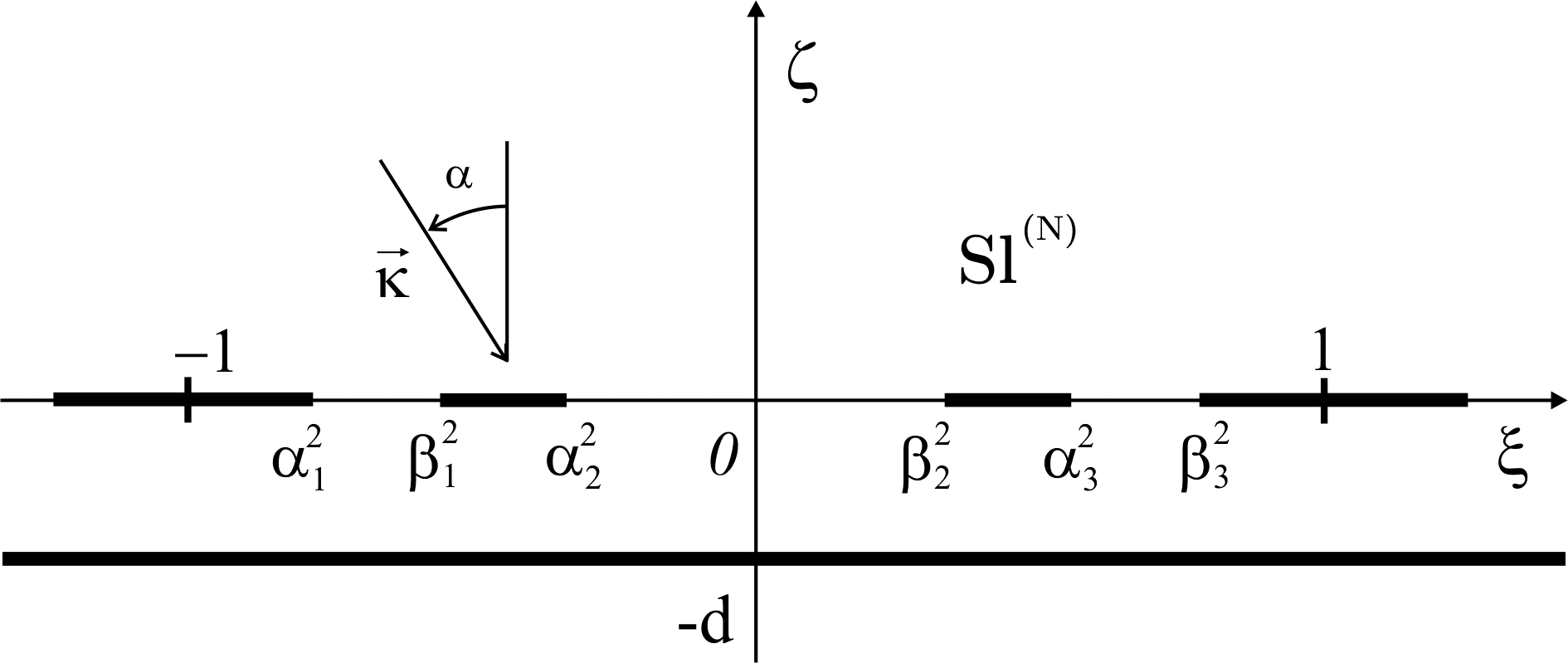 | Figure 5. Cross-section of the diffraction structure in the ξζ plane |
TE plane wave of unitary amplitude is incident from infinity onto the top of the diffraction structure (Fig. 5) at an angle α :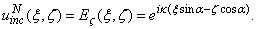 | (5) |
Here α is an angle between positive direction of the ζ axis and the propagation direction of a plane monochromatic wave, and κ is the absolute value of the wave vector.The total electric field has only 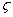 component
component 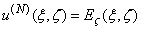 which can be represented as:
which can be represented as: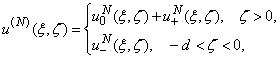 | (6) |
where 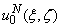 is a known solution of the Helmholtz equation when the slits are closed. The functions
is a known solution of the Helmholtz equation when the slits are closed. The functions 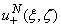 and
and 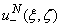 are to be determined. The total field should satisfy the following conditions:1. the Helmholtz equation above the flat screen reflector outside of the strips
are to be determined. The total field should satisfy the following conditions:1. the Helmholtz equation above the flat screen reflector outside of the strips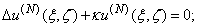 | (7) |
2. the boundary conditions on the strips: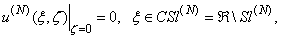 | (8) |
and on the flat screen reflector: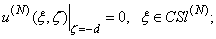 | (9) |
3. the conditions of conjugation in the slits: 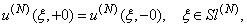 | (10) |
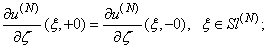 | (11) |
4. the Sommerfeld radiation conditions: 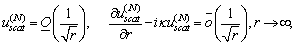 | (12) |
where 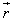 is the vector radius of the observation point;5. the Meixner edge condition (the local energy finiteness in any finite domain enclosing an edge point):
is the vector radius of the observation point;5. the Meixner edge condition (the local energy finiteness in any finite domain enclosing an edge point):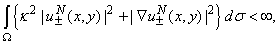 | (13) |
where Ω is any boundary field in 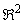 .The function
.The function 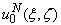 has the form:
has the form: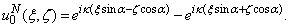 | (14) |
And functions 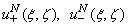 can be written as Fourier representation:
can be written as Fourier representation: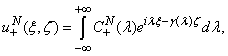 | (15) |
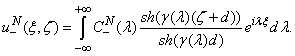 | (16) |
The radiation condition is satisfied if 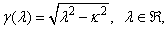 and is given by
and is given by 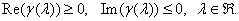 Such a scattering problem is uniquely solvable for the function
Such a scattering problem is uniquely solvable for the function 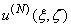 .We need to find the total field (6) which results from the scattering of E polarized monochromatic plane wave on considered diffraction structure.
.We need to find the total field (6) which results from the scattering of E polarized monochromatic plane wave on considered diffraction structure.
3. Hypersingular Integral Equation
Hypersingular integral equations[9], i.e., integral equations whose kernel has a singularity of an order greater than one (in our case the order singularity is two). HSIE is understood in the sense of finite part by Hadamard[8],[9].Substituting the expressions of functions (15) and (16) into the boundary conditions (8), (9), and into the conditions of conjugation in the slits (10), (11). Thus, obtain four equations: two into strips and two into slits. Using these equations and formula (14) the equality for coefficients 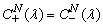 has been received for every lambda and a coupled integral equation should be written as:
has been received for every lambda and a coupled integral equation should be written as: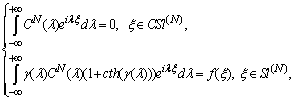 | (17) |
where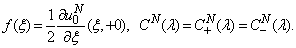 Following expression is introducing a new unknown function:
Following expression is introducing a new unknown function: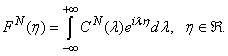 | (18) |
From the formula (17) following that, 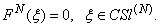 | (19) |
Using the inverse Fourier transform, a relation to the unknown coefficient can be defined: 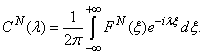 | (20) |
Denote,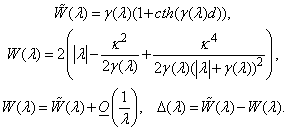 | (21) |
Using following relation 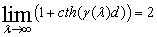 and formula (21), a second equation from (17) has the form:
and formula (21), a second equation from (17) has the form: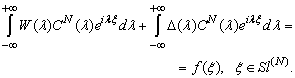 | (22) |
Use the expansion 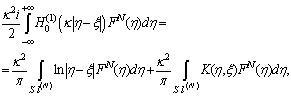 | (23) |
where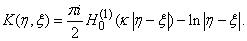 | (24) |
To lead the coupled integral equation (17) into hypersingular integral equations it is necessary to use specific parametric representations of the following form: • parametric representations[3] of hypersingular integral operator: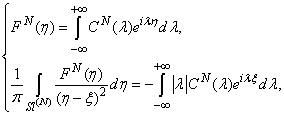 | (25) |
• integral operator with logarithmic singularity in the kernel: 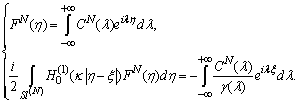 | (26) |
From the Equation (22) using formulas (23) - (26), the hypersingular integral equation can be obtained: 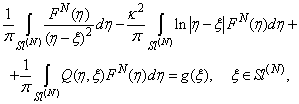 | (27) |
where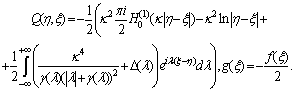 | (28) |
Mathematical model in equation (27) describes the solution for diffraction problem on screened pre-Cantor grating and is based on hypersingular integral equations.Introduce the restrictions of functions 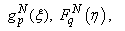 on intervals
on intervals 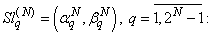
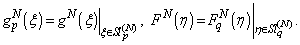 | (29) |
Thus, equation (27) can be written in the form for 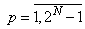 :
: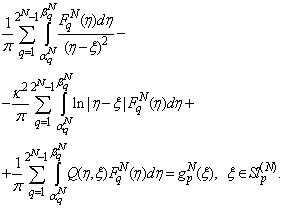 | (30) |
For the case if p=q: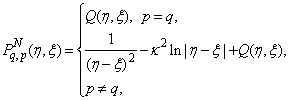 therefore, equation (30) can be transformed to:
therefore, equation (30) can be transformed to: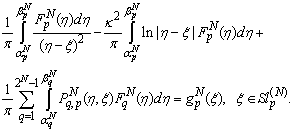 | (31) |
Standard interval (-1,1) has been chosen and is displayed to the intervals: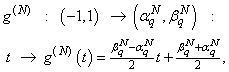 | (32) |
make the substitution for 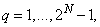
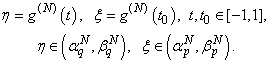 | (33) |
After simple transformations from (31) using (32), (33), HSIEs on standard intervals can be obtained :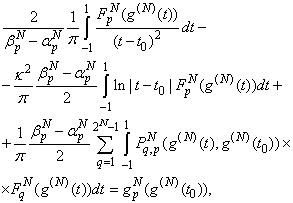 | (34) |
where 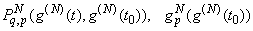 are smooth known functions:
are smooth known functions: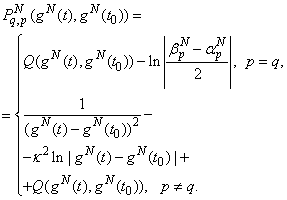 The Meixner edge condition will be satisfied if the unknown function (18) is represented in the form:
The Meixner edge condition will be satisfied if the unknown function (18) is represented in the form: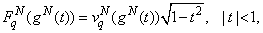 | (35) |
then equation (34) have a subsequent representation: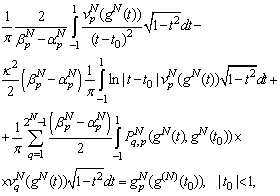 | (36) |
where 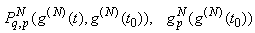 are smooth known functions.
are smooth known functions.
4. Discrete Mathematical Model
We can continue to improve our model when new information comes in. The most important step is numerical experiments which depicted some interesting phenomena. For example, the near-field has been of increasing interest, particularly in the development of capacitive sensing technologies such as those used in smart phones and tablet computers. And many other characteristics and parameters are important for future investigation of this particular task. Furthermore, discrete mathematics is the mathematical language of computer science, and as such, its importance has increased dramatically in recent decades. This is due to the fact that there are an increasing number of new software solutions to specific problems. For this reason, it is necessary to lead mathematical model (36) using discretization into discrete mathematical model for perform a numerical analysis.We build a discrete mathematical model based on equation (36) as follows. The first step is interpolated by a Lagrange polynomial of order (n-2) in the nodes which are the nulls of Chebyshev polynomials of the second kind[8]: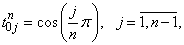 of the unknown function
of the unknown function 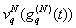 and smooth function
and smooth function 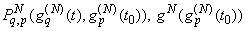 .On the next step, the specific quadrature formulas[8] of interpolation type with the equidistant grid of the polynomial of order (n-2) for integrals with hypersingular and logarithmic singularities and integrals of smooth functions are considered.
.On the next step, the specific quadrature formulas[8] of interpolation type with the equidistant grid of the polynomial of order (n-2) for integrals with hypersingular and logarithmic singularities and integrals of smooth functions are considered.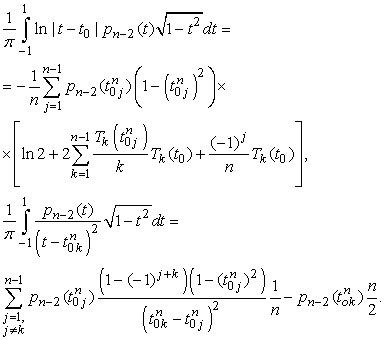 | (37) |
Interpolated polynomials for all functions in this problem coincide with initial functions in the node points: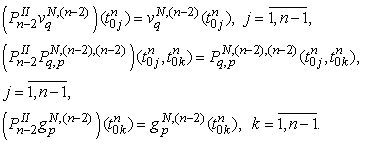 | (38) |
In such a way a system for approximate solutions from the mathematical model (36) is obtained. With the help of an efficient numerical discrete singularities method we got the system of linear algebraic equations for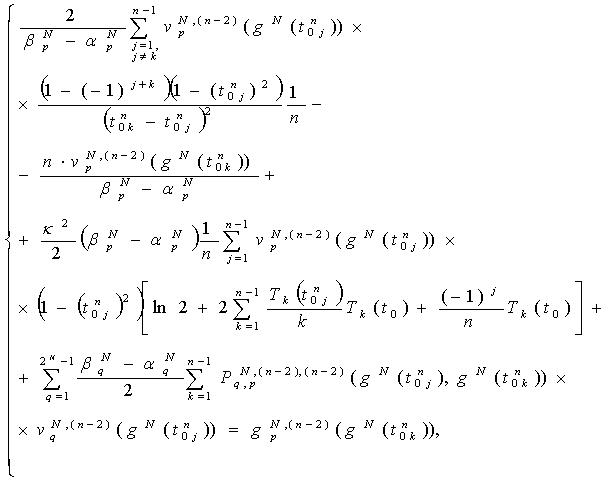 | (39) |
where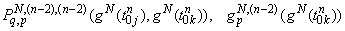 are smooth known functions.By solving the linear system (39) we find the values of unknown functions in the node points and calculate the unknown coefficient (20) to obtain the scattered and diffracted fields (15), (16). Using the asymptotic representation of the Hankel functions[12],[13] and functions in (15), (16), we derive the expressions for far field radiation patterns of the scattered and diffracted fields.The quality of the antenna is determined by its characteristics and parameters. Most antennas have directional properties. These properties are characterized by the radiation pattern. In consequence of this fact, necessity to calculate of the radiation pattern is major part of the numerical analysis. The analysis of various electromagnetic phenomena can be a very complicated task from the experimental point of view. The use of mathematical modelling, however, allows simulation of complex cases and sometimes is the only tool at hand of the engineer.In papers[6],[7], the numerical results for scattering problems on pre-Cantor impedance strips in cases of the TE and TM waves based on singular integral equations are discussed.
are smooth known functions.By solving the linear system (39) we find the values of unknown functions in the node points and calculate the unknown coefficient (20) to obtain the scattered and diffracted fields (15), (16). Using the asymptotic representation of the Hankel functions[12],[13] and functions in (15), (16), we derive the expressions for far field radiation patterns of the scattered and diffracted fields.The quality of the antenna is determined by its characteristics and parameters. Most antennas have directional properties. These properties are characterized by the radiation pattern. In consequence of this fact, necessity to calculate of the radiation pattern is major part of the numerical analysis. The analysis of various electromagnetic phenomena can be a very complicated task from the experimental point of view. The use of mathematical modelling, however, allows simulation of complex cases and sometimes is the only tool at hand of the engineer.In papers[6],[7], the numerical results for scattering problems on pre-Cantor impedance strips in cases of the TE and TM waves based on singular integral equations are discussed.
5. Conclusions
In this paper, a discrete mathematical model of the TE wave diffraction problem on screened pre-Cantor grating has been proposed. Mathematical model of this task is based on hypersingular integral equations. In order to resolve the HSIEs it is essential to use specific quadrature formulas for integrals with singularities. Investigation result of this work showed that the all difficulties with singularities in integrals are solved. Thus, it can be concluded that the overall aim of this article has been achieved. Discrete mathematical model of the diffraction problem on screened grating has been carried out. As show in the findings, the present investigations are actual and in-demand. Based on the obtained discrete mathematical model, the numerical experiments will be calculated with the help of an efficient discrete singularities method based on created discrete mathematical model. This experiment will be illustrated a main properties of scattered and diffracted fields such as diffraction and radiation patterns, field dependence on different characteristics and other. Future prospects in this field are investigation of 3-D diffraction problems on pre-fractal grating and carrying out numerical experiments.
ACKNOWLEDGEMENTS
The author would like to express her gratitude to the supervisor, Prof. Yuriy Gandel from Karazin Kharkiv National University (Kharkiv, Ukraine) for useful assistance, valuable advice, and continuous support. Besides, the author wishes to express her appreciation to Valiantsin Hardzeyeu from Ilmenau University of Technology (Ilmenau, Germany) for much attention and critical remarks while making this article.
References
| [1] | Gandel Yu. V., Dushkin V. D, Mathematical models of two-dimensional diffraction problems: Singular integral equations and numerical discrete singularities method (in Russian). Monograph. Kharkov: Academy of Internal Defence of the MIA of Ukraine, 2012. |
| [2] | Gandel Yu.V., Boundary - Value Problems for the Helmholtz Equation and their Discrete Mathematical Models. Journal of Mathematical Sciences, Springer Science + Business Media Inc. , 2010, Vol. 171, No. 1, pp. 74 - 88. |
| [3] | Gandel Yu. V., Double and hypersingular integral equation of the diffraction problem of electromagnetic waves on the plane gratings and screens (in Russian). Proceedings of the XI International Symposium "Discrete Singularities Methods in Mathematical Physics", 2003, pp. 53-58. |
| [4] | Nesvit K. V. Diffraction problem of H polarized electromagnetic waves by the bounded gratings with reflector. In print to Collection of articles «Contemporary problems of mathematics, mechanics and computing sciences». |
| [5] | Nesvit K. V, Hypersingular integral equation of the diffraction problem on screened pre-Cantor grating (in Russian). Proceedings of the XVI International Symposium «Discrete Singularities Methods in Mathematical Physics» (DSMMPh-2013), Kharkiv, Kherson, 2013, pp. 293-297. |
| [6] | Nesvit K. V., Discrete mathematical model of diffraction on pre-Cantor set of slits in impedance plane and numerical experiment. International Journal of Mathematical Models and Methods in Applied Sciences, Issue 11, Vol. 7, 2013, pp. 897-906.http://www.naun.org/main/NAUN/ijmmas/k012001-086.pdf |
| [7] | Nesvit K. V., Discrete mathematical model of wave diffraction on pre-fractal impedance strips. TM mode case. AIP Conference Proceedings: Application of Mathematics in Technical and Natural Sciences: 5th International Conference for Promoting the Application of Mathematics in Technical and Natural Sciences - AMiTaNS 13. DOI: 10.1063/ 1.4827231. Vol. 1561, 2013, pp. 219-223. |
| [8] | Gandel Yu. V., Introduction to methods of evaluation of singular and hypersingular integrals (in Russian). Textbook. - Kharkov, 2002. |
| [9] | Lifanov I. K., Poltavskii L. N., Vainikko G. M., Hypersingular Integral Equations and their application. London. New York. Washington: CRC Press, 2004. |
| [10] | Gandel Yu.V., Eremenko S.V., Polyanskaya T.S., Mathematical problems in the method of discrete currents. Justification of the numerical method of discrete singularities of solutions of two-dimensional problems of diffraction of electromagnetic waves (in Russian). Educational aid. Part II. Kharkov: Kharkov State University, 1992. |
| [11] | Mandelbrot B. B., The Fractal Geometry of Nature, W.H. Freeman and Company, New York, 1983. |
| [12] | Gandel Yu. V., Elementary asymptotic estimate of the integrals (in Russian). Textbook. Rota-print of Kharkiv State University, 1977. |
| [13] | Watson G. N., A Treatise on the Theory of Bessel Functions. Cambridge At The University Press, 1922. |




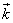 (see Fig. 4).Cartesian coordinate system is chosen so that the set of the strips is located in XY plane, and the X axis is parallel to the strips’ edges (see Fig. 4).
(see Fig. 4).Cartesian coordinate system is chosen so that the set of the strips is located in XY plane, and the X axis is parallel to the strips’ edges (see Fig. 4).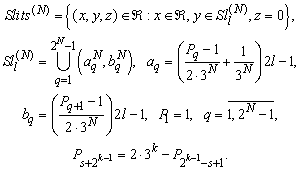
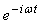 and omitted.The unique non-zero independent component of the electric field satisfies the two-dimensional Helmholtz equation above the flat screen reflector and without the strips:
and omitted.The unique non-zero independent component of the electric field satisfies the two-dimensional Helmholtz equation above the flat screen reflector and without the strips: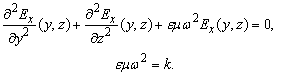

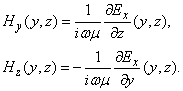
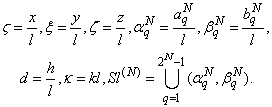
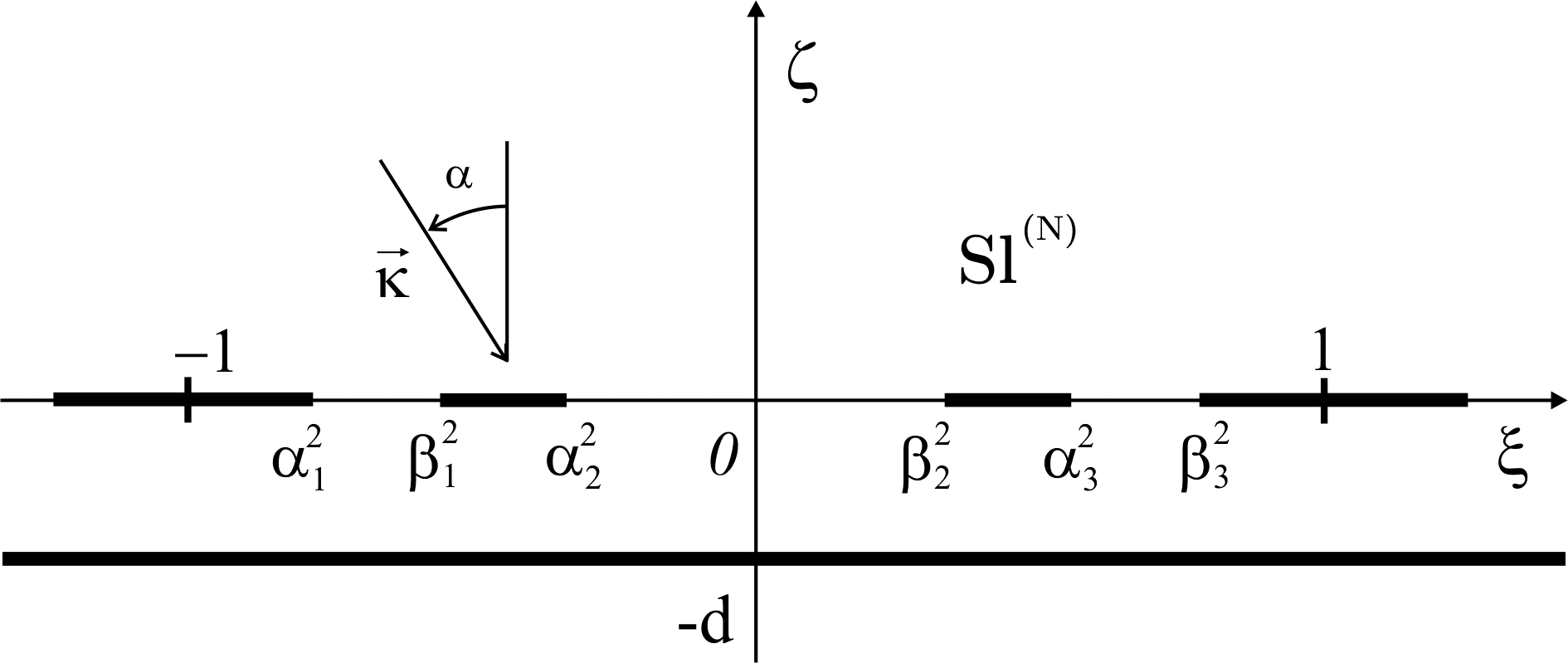
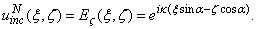
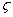 component
component 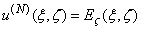 which can be represented as:
which can be represented as: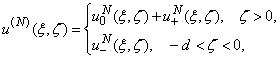
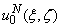 is a known solution of the Helmholtz equation when the slits are closed. The functions
is a known solution of the Helmholtz equation when the slits are closed. The functions 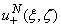 and
and 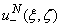 are to be determined. The total field should satisfy the following conditions:1. the Helmholtz equation above the flat screen reflector outside of the strips
are to be determined. The total field should satisfy the following conditions:1. the Helmholtz equation above the flat screen reflector outside of the strips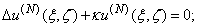
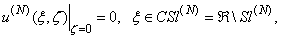
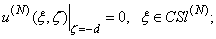
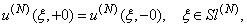
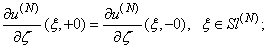
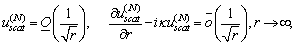
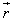 is the vector radius of the observation point;5. the Meixner edge condition (the local energy finiteness in any finite domain enclosing an edge point):
is the vector radius of the observation point;5. the Meixner edge condition (the local energy finiteness in any finite domain enclosing an edge point):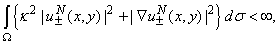
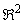 .The function
.The function 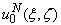 has the form:
has the form: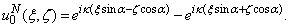
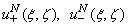 can be written as Fourier representation:
can be written as Fourier representation: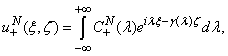
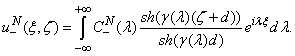
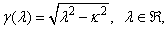 and is given by
and is given by 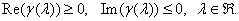 Such a scattering problem is uniquely solvable for the function
Such a scattering problem is uniquely solvable for the function 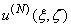 .We need to find the total field (6) which results from the scattering of E polarized monochromatic plane wave on considered diffraction structure.
.We need to find the total field (6) which results from the scattering of E polarized monochromatic plane wave on considered diffraction structure.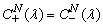 has been received for every lambda and a coupled integral equation should be written as:
has been received for every lambda and a coupled integral equation should be written as: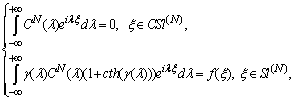
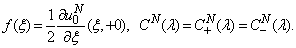 Following expression is introducing a new unknown function:
Following expression is introducing a new unknown function: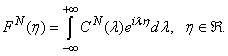
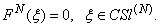
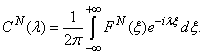
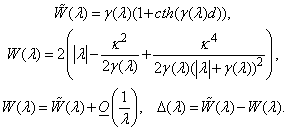
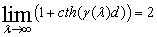 and formula (21), a second equation from (17) has the form:
and formula (21), a second equation from (17) has the form: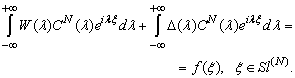
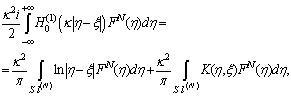
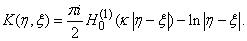
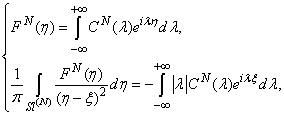
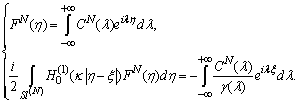
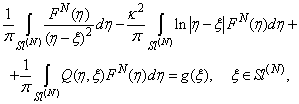
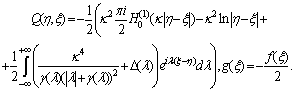
 on intervals
on intervals 
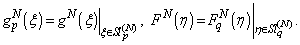
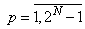 :
: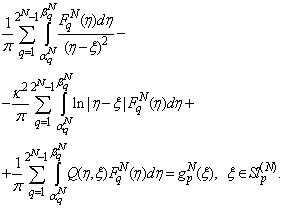
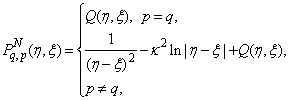 therefore, equation (30) can be transformed to:
therefore, equation (30) can be transformed to: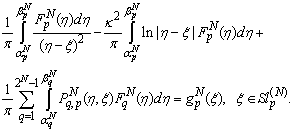
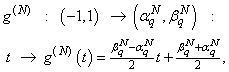
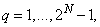
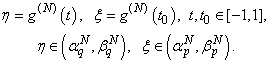
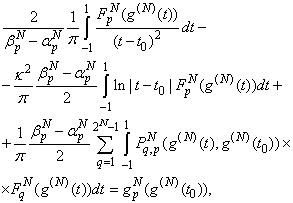
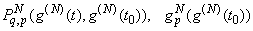 are smooth known functions:
are smooth known functions: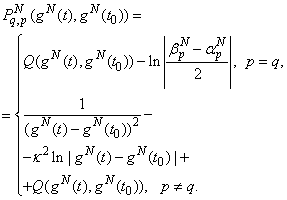 The Meixner edge condition will be satisfied if the unknown function (18) is represented in the form:
The Meixner edge condition will be satisfied if the unknown function (18) is represented in the form: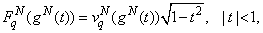
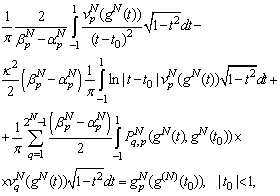
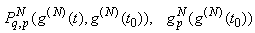 are smooth known functions.
are smooth known functions.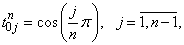 of the unknown function
of the unknown function 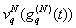 and smooth function
and smooth function 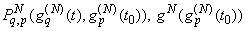 .On the next step, the specific quadrature formulas[8] of interpolation type with the equidistant grid of the polynomial of order (n-2) for integrals with hypersingular and logarithmic singularities and integrals of smooth functions are considered.
.On the next step, the specific quadrature formulas[8] of interpolation type with the equidistant grid of the polynomial of order (n-2) for integrals with hypersingular and logarithmic singularities and integrals of smooth functions are considered.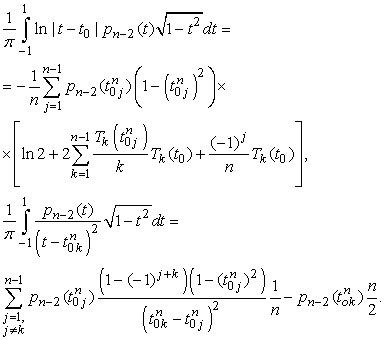
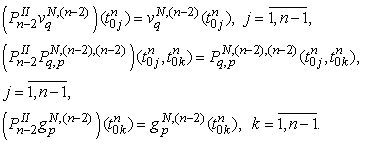
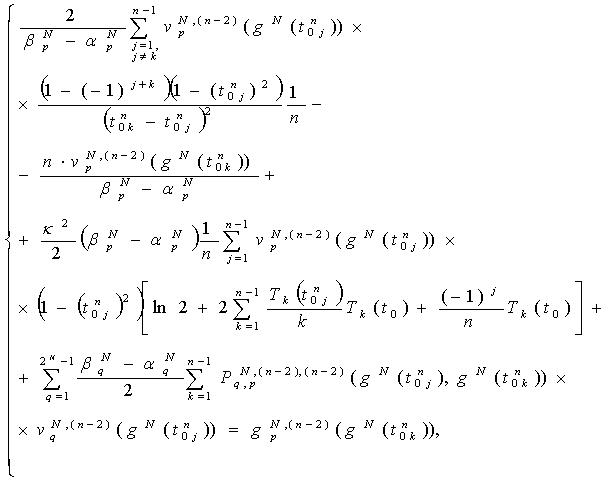
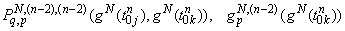 are smooth known functions.By solving the linear system (39) we find the values of unknown functions in the node points and calculate the unknown coefficient (20) to obtain the scattered and diffracted fields (15), (16). Using the asymptotic representation of the Hankel functions[12],[13] and functions in (15), (16), we derive the expressions for far field radiation patterns of the scattered and diffracted fields.The quality of the antenna is determined by its characteristics and parameters. Most antennas have directional properties. These properties are characterized by the radiation pattern. In consequence of this fact, necessity to calculate of the radiation pattern is major part of the numerical analysis. The analysis of various electromagnetic phenomena can be a very complicated task from the experimental point of view. The use of mathematical modelling, however, allows simulation of complex cases and sometimes is the only tool at hand of the engineer.In papers[6],[7], the numerical results for scattering problems on pre-Cantor impedance strips in cases of the TE and TM waves based on singular integral equations are discussed.
are smooth known functions.By solving the linear system (39) we find the values of unknown functions in the node points and calculate the unknown coefficient (20) to obtain the scattered and diffracted fields (15), (16). Using the asymptotic representation of the Hankel functions[12],[13] and functions in (15), (16), we derive the expressions for far field radiation patterns of the scattered and diffracted fields.The quality of the antenna is determined by its characteristics and parameters. Most antennas have directional properties. These properties are characterized by the radiation pattern. In consequence of this fact, necessity to calculate of the radiation pattern is major part of the numerical analysis. The analysis of various electromagnetic phenomena can be a very complicated task from the experimental point of view. The use of mathematical modelling, however, allows simulation of complex cases and sometimes is the only tool at hand of the engineer.In papers[6],[7], the numerical results for scattering problems on pre-Cantor impedance strips in cases of the TE and TM waves based on singular integral equations are discussed. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML