-
Paper Information
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Computational and Applied Mathematics
p-ISSN: 2165-8935 e-ISSN: 2165-8943
2013; 3(6): 283-290
doi:10.5923/j.ajcam.20130306.03
Extended Block Integrator for First-Order Stiff and Oscillatory Differential Equations
J. Sunday1, M. R. Odekunle2, A. O. Adesanya2, A. A. James3
1Department of Mathematical Sciences, Adamawa State University, Mubi, Nigeria
2Department of Mathematics, Modibbo Adama University of Technology, Yola, Nigeria
3Mathematics Division, American University of Nigeria, Yola, Nigeria
Correspondence to: J. Sunday, Department of Mathematical Sciences, Adamawa State University, Mubi, Nigeria.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
In this paper, we consider the development of an extended block integrator for the solution of stiff and oscillatory first-order Ordinary Differential Equations (ODEs) using interpolation and collocation techniques. The integrator was developed by collocation and interpolation of the combination of power series and exponential function to generate a continuous implicit Linear Multistep Method (LMM). The paper further investigates the basic properties of the block integrator and found it to be zero-stable, consistent and convergent. The integrator was also tested on some sampled stiff and oscillatory problems and found to perform better than some existing ones.
Keywords: Extended Block Integrator, Exponential Function, Oscillatory, Power Series, Stiff
Cite this paper: J. Sunday, M. R. Odekunle, A. O. Adesanya, A. A. James, Extended Block Integrator for First-Order Stiff and Oscillatory Differential Equations, American Journal of Computational and Applied Mathematics , Vol. 3 No. 6, 2013, pp. 283-290. doi: 10.5923/j.ajcam.20130306.03.
Article Outline
1. Introduction
- In this paper, we consider the numerical solution of stiff and oscillatory first-order differential equations of the form,
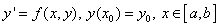 | (1) |
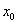 is the initial point,
is the initial point, 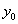 is the solution at the initial point and
is the solution at the initial point and 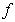 is assumed to satisfy Lipchitz condition stated below.Theorem 1[13]: Let
is assumed to satisfy Lipchitz condition stated below.Theorem 1[13]: Let 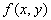 be defined and continuous for all points
be defined and continuous for all points 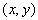 in the region
in the region 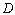 defined by
defined by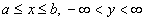 ,
, 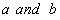 finite, and let there exist a constant
finite, and let there exist a constant 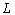 such that, for every
such that, for every 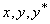 such that
such that 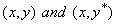 are both in
are both in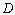 ;
;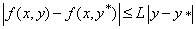 Then, if
Then, if 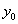 is any given number, there exists a unique solution
is any given number, there exists a unique solution 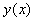 of the initial value problem (1), where
of the initial value problem (1), where 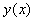 is continuous and differentiable for all
is continuous and differentiable for all 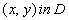 .Proof, see[11]According to[18], equation (1) is used in simulating the growth of population, trajectory of particles, simple harmonic motion, deflection of a beam, etc. Few equations that are modeled in higher order differential equations are first reduced to systems of first-order before appropriate method of solution is applied. Most often, these problems do not have a closed form solutions, hence appropriate methods are adopted to solve such problems. Different methods have been proposed ranging from predictor-corrector methods to block methods. Despite the success recorded by the predictor-corrector methods, its major setback is that the predictors are in reducing order of accuracy especially when the value of the step-length is high and moreover the results are at overlapping interval[3]. Block methods which have advantage of being more efficient in terms of cost implementation, time of execution and accuracy were developed to handle the setbacks of predictor-corrector methods[19],[2] and[20].Definition 1[13]: A differential equation is said to be stiff if
.Proof, see[11]According to[18], equation (1) is used in simulating the growth of population, trajectory of particles, simple harmonic motion, deflection of a beam, etc. Few equations that are modeled in higher order differential equations are first reduced to systems of first-order before appropriate method of solution is applied. Most often, these problems do not have a closed form solutions, hence appropriate methods are adopted to solve such problems. Different methods have been proposed ranging from predictor-corrector methods to block methods. Despite the success recorded by the predictor-corrector methods, its major setback is that the predictors are in reducing order of accuracy especially when the value of the step-length is high and moreover the results are at overlapping interval[3]. Block methods which have advantage of being more efficient in terms of cost implementation, time of execution and accuracy were developed to handle the setbacks of predictor-corrector methods[19],[2] and[20].Definition 1[13]: A differential equation is said to be stiff if 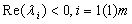 , where
, where 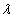 is the eigen value of the differential equation. Definition 2[6]: A nontrivial solution (function) of an ODE is called oscillating if it does not tend either to a finite limit or to infinity (i.e. if it has an infinite number of roots). The differential equation is called oscillating, if it has at least one oscillating solution.In the quest for a method that gives better stability condition, [14] proposed an approximate solution which combined power series and exponential function. In this paper, we extend their work by developing a block integrator with step number k=5.
is the eigen value of the differential equation. Definition 2[6]: A nontrivial solution (function) of an ODE is called oscillating if it does not tend either to a finite limit or to infinity (i.e. if it has an infinite number of roots). The differential equation is called oscillating, if it has at least one oscillating solution.In the quest for a method that gives better stability condition, [14] proposed an approximate solution which combined power series and exponential function. In this paper, we extend their work by developing a block integrator with step number k=5. 2. Derivation of the Extended Block Integrator
- We consider an approximate solution that combines power series and exponential function of the form,
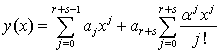 | (2) |
 at a grid point and collocation points
at a grid point and collocation points  at all points giving rise to
at all points giving rise to 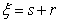 system of equations whose coefficients are determined by using appropriate procedures. The first derivative of (2) is given by,
system of equations whose coefficients are determined by using appropriate procedures. The first derivative of (2) is given by,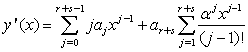 | (3) |
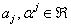 for
for 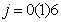 and
and 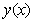 is continuously differentiable. Let the solution of (1) be sought on the partition
is continuously differentiable. Let the solution of (1) be sought on the partition 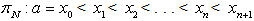
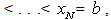 of the integration interval
of the integration interval 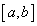 with a constant step-size
with a constant step-size 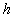 , given by,
, given by, 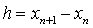 ,
, 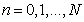 .Then, substituting (3) in (1) gives,
.Then, substituting (3) in (1) gives,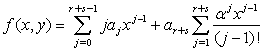 | (4) |
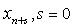 and collocating (4) at points
and collocating (4) at points 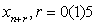 , leads to the following system of equations,
, leads to the following system of equations, 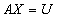 | (5) |
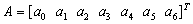
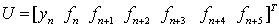 and
and  Solving (5), for
Solving (5), for 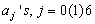 and substituting back into (2) gives a continuous linear multistep method of the form,
and substituting back into (2) gives a continuous linear multistep method of the form,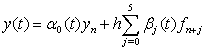 | (6) |
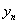 and
and 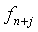 are given by,
are given by, | (7) |
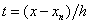 . Evaluating (6) at
. Evaluating (6) at 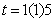 gives a block scheme of the form,
gives a block scheme of the form,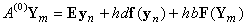 | (8) |
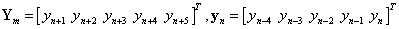 ,
,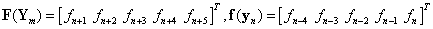 ,
,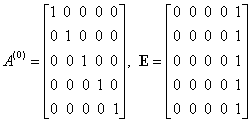 ,
, ,
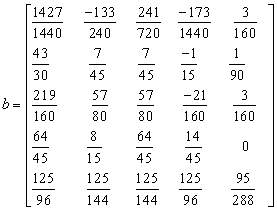
, 
3. Analysis of Basic Properties of the Extended Block Integrator
3.1. Order of the Extended Block Integrator
- Let the linear operator
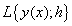 associated with the block (8) be defined as,
associated with the block (8) be defined as,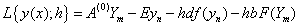 | (9) |
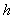 gives,
gives, 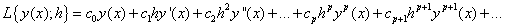 | (10) |
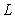 and the associated continuous linear multistep method (6) are said to be of order
and the associated continuous linear multistep method (6) are said to be of order 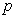 if
if 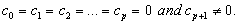
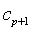 is called the error constant and the local truncation error is given by,
is called the error constant and the local truncation error is given by,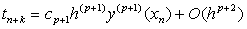 | (11) |
 | (12) |
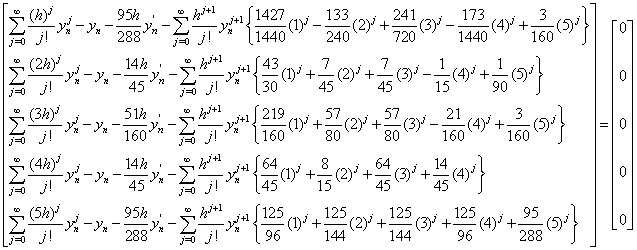 | (13) |
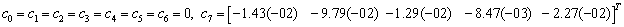 Therefore, the extended block integrator is of order six.
Therefore, the extended block integrator is of order six.3.2. Zero Stability
- Definition 4[10]: The block integrator (8) is said to be zero-stable, if the roots
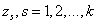 of the first characteristic polynomial
of the first characteristic polynomial 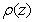 defined by
defined by 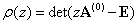 satisfies
satisfies 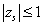 and every root satisfying
and every root satisfying 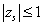 have multiplicity not exceeding the order of the differential equation. Moreover, as
have multiplicity not exceeding the order of the differential equation. Moreover, as 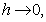
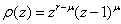 where
where 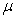 is the order of the differential equation,
is the order of the differential equation, 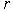 is the order of the matrices
is the order of the matrices 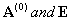 , see[5] for details. For our integrator,
, see[5] for details. For our integrator, | (14) |
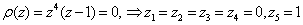 . Hence, the extended block integrator is zero-stable.
. Hence, the extended block integrator is zero-stable.3.3. Consistency
- The extended block integrator (8) is consistent since it has order
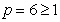 .
.3.4. Convergence
- The extended block integrator is convergent by consequence of Dahlquist theorem stated below.Theorem 2[8]: The necessary and sufficient conditions that a continuous LMM be convergent are that it be consistent and zero-stable.
3.5. Region of Absolute Stability
- Definition 5[22]: Region of absolute stability is a region in the complex
 plane, where
plane, where 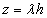 . It is defined as those values of
. It is defined as those values of 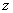 such that the numerical solutions of
such that the numerical solutions of 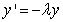 satisfy
satisfy 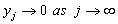 for any initial condition.We shall adopt the boundary locus method to determine the region of absolute stability of the extended block integrator. This is achieved by substituting the test equation,
for any initial condition.We shall adopt the boundary locus method to determine the region of absolute stability of the extended block integrator. This is achieved by substituting the test equation,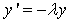 | (15) |
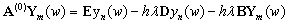 | (16) |
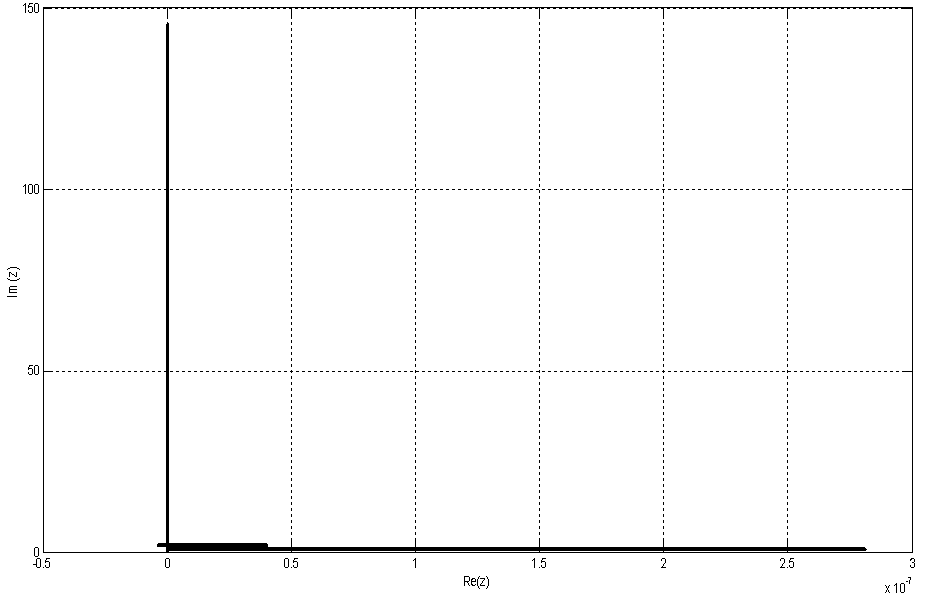 | Figure 1. Showing the Stability Region of the Extended Block Integrator |
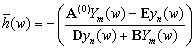 | (17) |
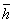 is given by
is given by 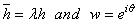 . Equation (17) is our characteristic/stability polynomial. For the extended block integrator, equation (17) is given by,
. Equation (17) is our characteristic/stability polynomial. For the extended block integrator, equation (17) is given by,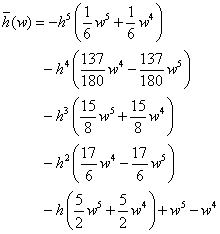 | (18) |
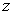 plane. Thus, the extended block integrator is L-stable.
plane. Thus, the extended block integrator is L-stable.4. Numerical Experiments
- We shall evaluate the performance of the block integrator on some challenging stiff and oscillatory problems which have appeared in literature and compare the results with solutions from some methods of similar derivation. The numerical results are obtained using MATLAB.The following notations shall be used in the tables below;ERR- Exact Solution-Computed SolutionESSI- Error in[17]ESYO- Error in[20]Problem 1Consider the highly stiff ODE
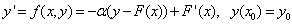 | (19) |
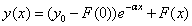 | (20) |
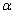 is a positive constant and
is a positive constant and 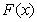 is a smooth slowly varying function. Equation (20) exhibits two widely different time scales: a rapidly changing term associated with
is a smooth slowly varying function. Equation (20) exhibits two widely different time scales: a rapidly changing term associated with 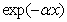 and a slowly varying term associated with
and a slowly varying term associated with 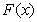 . In[17], the authors considered a special case of (19) where
. In[17], the authors considered a special case of (19) where 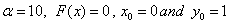 . They solved the problem 1 by adopting an L-stable hybrid block Simpson’s method of order six. The authors in[20] also solved problem 1 using a block integrator with step number
. They solved the problem 1 by adopting an L-stable hybrid block Simpson’s method of order six. The authors in[20] also solved problem 1 using a block integrator with step number 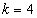 .Problem 2Consider the highly oscillatory ODE
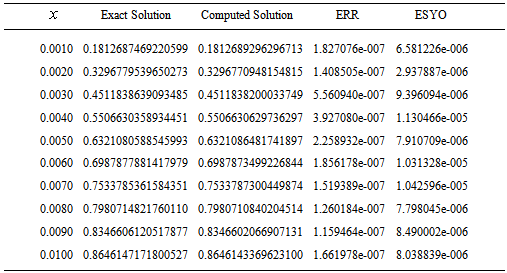
.Problem 2Consider the highly oscillatory ODE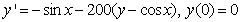 | (21) |
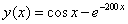 | (22) |
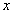 . He further stated that most numerical methods do not perform well on this problem. The authors in[20] solved problem 2 by adopting a block integrator with step number
. He further stated that most numerical methods do not perform well on this problem. The authors in[20] solved problem 2 by adopting a block integrator with step number 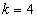 .
.
|
|
5. Conclusions
- In this paper, we have presented an extended block integrator for the solution of stiff and oscillatory first-order ordinary differential equations. Our aim was to construct highly stable block integrator which is computationally more efficient than many of the existing numerical integrators for stiff and oscillatory problems. The approximate solution (basis function) adopted in this paper produced a block integrator with L-stable stability region. This made it possible for the block integrator to perform well on stiff and oscillatory problems. The extended block integrator proposed was also found to be zero-stable, consistent and convergent. The block integrator was also found to perform better than some existing methods in view of the numerical results presented.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML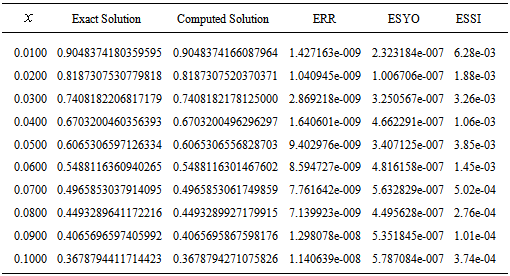
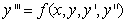 , American J. of Computational Mathematics, 3, 169-174, 2013.
, American J. of Computational Mathematics, 3, 169-174, 2013.