S. K. Mutua1, M. E. Kimathi2, P. R. Kiogora1, N. M. Mutua3
1Faculty of Science, Pure & Applied Mathematics Department, Jomo Kenyatta University of Agriculture & Technology, Nairobi, 62000-00200, Kenya
2School of Mathematics & Statistics, Pure & Applied Mathematics Department, Technical University of Kenya, Nairobi, 52428-00200, Kenya
3School of Science & Informatics, Mathematics and Informatics Department, Taita Taveta University College, Voi, 635-80300, Kenya
Correspondence to: N. M. Mutua, School of Science & Informatics, Mathematics and Informatics Department, Taita Taveta University College, Voi, 635-80300, Kenya.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
In this paper we deal with the Euler equations for Isothermal gas. In analyzing the equations we obtain two real and distinct eigenvalues which enables us to determine the wave structure of the possible solutions to the Riemann problem set up. By considering the Rankine-Hugoniot condition we obtain the shock wave solution analytically. The rarefaction wave solution is determined analytically by considering the fact that rarefaction wave lies along integral curves. To obtain the numerical solution to the Riemann problem that we set up, we use a relaxation scheme to discretize the Euler equations for isothermal gas. Finally we present the simulation results of the numerical solutions, that is, the approximate shock and rarefaction wave solutions are shown, graphically, and explained.
Keywords:
Isothermal Gas, Eigenvalues, Riemann Problem, Rankine-Hugonoit, Integral Curves, Relaxation Scheme
Cite this paper: S. K. Mutua, M. E. Kimathi, P. R. Kiogora, N. M. Mutua, A Study of Solutions to Euler Equations for a One Dimensional Unsteady Flow, American Journal of Computational and Applied Mathematics , Vol. 3 No. 4, 2013, pp. 233-237. doi: 10.5923/j.ajcam.20130304.06.
1. Introduction
Consider the Euler equations for isothermal gas. The system consists of Euler equations and is strictly hyperbolic with two real and distinct eigenvalues, whereby one is greater than the other. Depending on the initial data the eigenvalues may represent shock and rarefaction waves. The resolution of the discontinuities of a self-similar solution of the compressible Euler equation is sharper than the corresponding initial value solution, Ravi[4].A shock tube problem is the study of the propagation of shock waves in a one dimensional tube. The energy of a shock wave dissipates relatively quickly within distance. Moving shocks are usually generated by the interaction of two bodies of gas at different pressure, with a shock wave propagating into the lower pressure gas and an expansion wave propagating into the higher pressure gas. The numerical computation of the shock tube problem by means on F wave digital principle showed that the MD Kichoffs network can successfully be extended by taking viscosity into account to represent the Navier Stokes equation Mengel[2].A Riemann problem consists of equations together with the discontinuous initial data. The numerical dissipation of eight different schemes and five delimiters to numerical computation of the Riemann problem compared to the resolution of discontinuities of each scheme were vital to improving the schemes accuracy and stability, Wang et al[8].
2. Mathematical Formulation of the Euler Equations
The Euler equations is derived from Newton’s Second law of motion and is a system of conservation laws that can be written in the form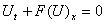 | (2.1) |
Where U and F(U) are the vectors of conserved variables and fluxes, given respectively by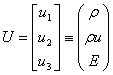 ,
, 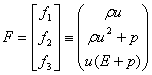 Where
Where 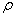 is density, p is pressure, u is the particle velocity and E is the total energy per unit volume.Under the assumption that the entropy, s, is a constant everywhere, which is a simplification of the thermodynamics. Now the EOS is
is density, p is pressure, u is the particle velocity and E is the total energy per unit volume.Under the assumption that the entropy, s, is a constant everywhere, which is a simplification of the thermodynamics. Now the EOS is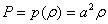 | (2.2) |
Where a is the wave propagation speed.Under this assumption the energy equation becomes redundant and thus we have a 2X2 system. This makes equation 2.1 to be: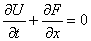 | (2.3) |
Where 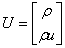
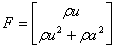 Thus we have,
Thus we have,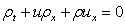 | (2.4) |
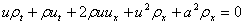 | (2.5) |
Now using equation 2.5 we have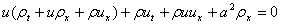 , thus the two equations can be written as:
, thus the two equations can be written as: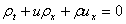 ,
,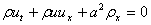 which can be written in matrix form as:
which can be written in matrix form as: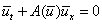 Where
Where 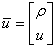 ,
, 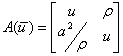 Now to get the eigenvalues for the matrix
Now to get the eigenvalues for the matrix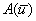 , we use the manipulation
, we use the manipulation 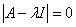
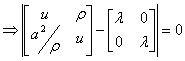 , which gives rise to a quadratic equation with real roots
, which gives rise to a quadratic equation with real roots 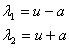 | (2.6) |
Since the eigenvalues exist and are real values, thus the equation can be said to be hyperbolic. Now to get the eigenvectors for the corresponding eigenvalues we use 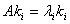 where
where 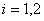 Thus using the first eigenvalue,
Thus using the first eigenvalue, 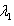 , we have:
, we have: 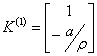 , as the corresponding eigenvector, while using the second eigenvalues,
, as the corresponding eigenvector, while using the second eigenvalues, 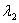 , we have:
, we have: 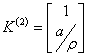 as the corresponding eigenvector.From the above eigenvalues and eigenvectors then we can be able to determine the structure of the waves that is by considering the Riemann’s problem defined by
as the corresponding eigenvector.From the above eigenvalues and eigenvectors then we can be able to determine the structure of the waves that is by considering the Riemann’s problem defined by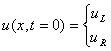
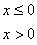 The solution to this problem depends on the relative values of
The solution to this problem depends on the relative values of 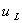 and
and 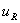 . That is, for
. That is, for 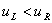 , a rarefaction wave is going to develop while for
, a rarefaction wave is going to develop while for 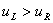 , a shock wave is going to appear. Thus for a case where no vacuum is present the exact solutions will have the two different waves which would be associated with the eigenvalues 2.6.
, a shock wave is going to appear. Thus for a case where no vacuum is present the exact solutions will have the two different waves which would be associated with the eigenvalues 2.6.
3. Analytical Solution
Now to get the analytical solution for the shock wave for both the left and right shocks, we apply the Rankine-Hugoniot condition to the system that is,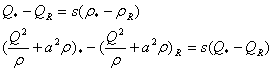 This gives two equations with three unknowns, that is,
This gives two equations with three unknowns, that is, 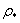 ,
, 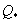 and s, which can easily be solved for
and s, which can easily be solved for 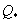 and s in terms of
and s in terms of 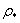 , Leveque[3]
, Leveque[3]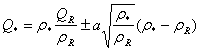 | (3.1) |
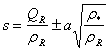 | (3.2) |
In equations 3.1 and 3.2 it remains to express in terms of the known values 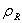 . For instance, in Leveque[3], we parametize the curves by taking
. For instance, in Leveque[3], we parametize the curves by taking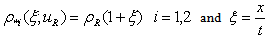 We then have
We then have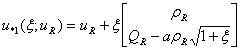 ,
,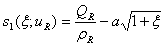 and
and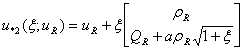 ,
,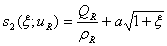 Also the rarefaction wave solution takes the form
Also the rarefaction wave solution takes the form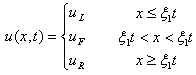 Since the rarefactions lie along the integral curve, Leveque[3], we consider the following equation.
Since the rarefactions lie along the integral curve, Leveque[3], we consider the following equation.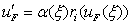 Where
Where 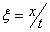 ,
, 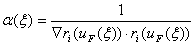
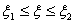 Therefore,
Therefore,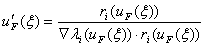
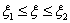 With initial data
With initial data 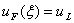 , where
, where 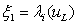 and
and 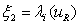 Now, using the first eigenvalue and equation 3.1, we can be able to construct the 1-rarefactions for the equations, thus the system of ODE’s takes the form
Now, using the first eigenvalue and equation 3.1, we can be able to construct the 1-rarefactions for the equations, thus the system of ODE’s takes the form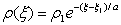
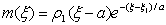 Where on eliminating
Where on eliminating 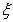 to solve for m as a function of
to solve for m as a function of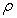 , we have
, we have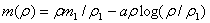 | (3.3) |
Similarly, using the second eigenvalue to construct the 2-rarefactions, we have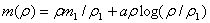 | (3.4) |
4. Numerical Solution Using the Relaxation Scheme
Now, for us to solve the Euler equation 2.3 numerically we will use the relaxation scheme, since it they are stable and conservative discretizations of the original conservation laws.In equation 2.3 we had, 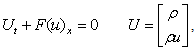
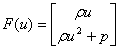 With initial data
With initial data 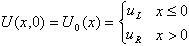 Now introducing the relaxation system, we have
Now introducing the relaxation system, we have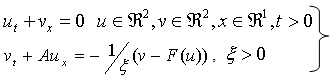 | (4.1) |
Where 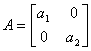 , is a positive diagonal matrix to be chosen.For
, is a positive diagonal matrix to be chosen.For 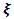 sufficiently small, it is expected that by solving (4.1) properly, one can obtain good approximations to the original conservation lawsThe positive constant a need satisfy: Shi J. et a l [5],
sufficiently small, it is expected that by solving (4.1) properly, one can obtain good approximations to the original conservation lawsThe positive constant a need satisfy: Shi J. et a l [5], 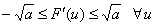 For the relaxation system (4.1), the initial data is:
For the relaxation system (4.1), the initial data is: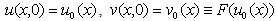 , Now introducing the spatial grid points
, Now introducing the spatial grid points 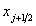 with mesh width
with mesh width 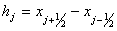 while the discrete time level
while the discrete time level 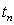 are spaced uniformly with space step
are spaced uniformly with space step 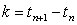 for n=0, 1, 2.Here we denote by
for n=0, 1, 2.Here we denote by 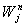 the approximate cell average of a quantity W in the cell
the approximate cell average of a quantity W in the cell 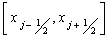 at time
at time 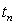 and by
and by 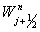 the approximate point value of W at
the approximate point value of W at  and
and 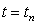 .A spatial discretization to equation 4.1 in conservation form can be written as:
.A spatial discretization to equation 4.1 in conservation form can be written as: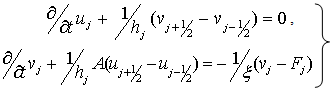 | (4.2) |
Where the averaged quantity Fj is defined by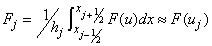 Since the relaxation system 4.1 has two characteristic variables, see Shi J. et al 5,
Since the relaxation system 4.1 has two characteristic variables, see Shi J. et al 5,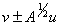 | (4.3) |
that travel with the frozen characteristic speeds 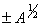 respectively.For better accuracy we use a second-order scheme that is the Van Leer’s MUSCL scheme, see Van Leer[7].Applying this scheme to the pth component that is equation 4.3, gives
respectively.For better accuracy we use a second-order scheme that is the Van Leer’s MUSCL scheme, see Van Leer[7].Applying this scheme to the pth component that is equation 4.3, gives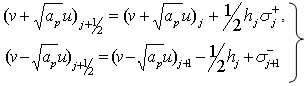 | (4.4) |
Where 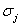 is the slope of
is the slope of 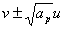 on the j-th cell which we define using Sweby’s notation, see Sweby[6].
on the j-th cell which we define using Sweby’s notation, see Sweby[6].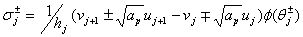 ,
,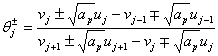 Where
Where 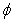 is a slope-limiter function given as, Van Leer[7]
is a slope-limiter function given as, Van Leer[7]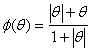 Solving equations 4.4 for
Solving equations 4.4 for 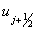 and
and 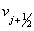 gives
gives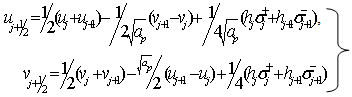 | (4.5) |
Applying 4.5 in 4.4 we have,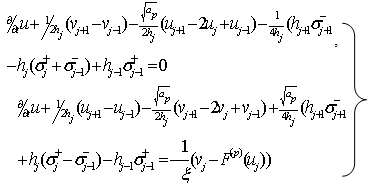 | (4.6) |
Where 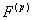 is the p-th component of F.Since the one dimensional Euler equation 2.3 has two eigen values
is the p-th component of F.Since the one dimensional Euler equation 2.3 has two eigen values 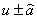 we take
we take 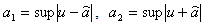 , Now, to obtain the time discretization for the relaxation scheme we use a second-order TVD Runge-Kutta splitting scheme which was introduced by Jin, Shi J. et al[5]Denote
, Now, to obtain the time discretization for the relaxation scheme we use a second-order TVD Runge-Kutta splitting scheme which was introduced by Jin, Shi J. et al[5]Denote 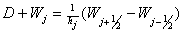 Then applying the second-order TVD Runge-Kutta splitting scheme to the time derivative in 4.6, that is applying it to 4.1 yields
Then applying the second-order TVD Runge-Kutta splitting scheme to the time derivative in 4.6, that is applying it to 4.1 yields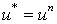 ,
,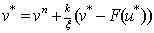 ;
;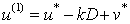 ,
,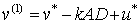 ;
;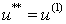 ,
,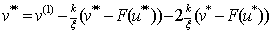 ;
;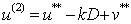 ,
,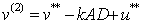 ;
;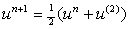 ,
,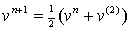 ;
;
5. Simulation
We use the value of h as 0.005 but choose the time step, k, according to Courant-Friedrichs-Lewy (CFL) condition. 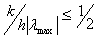 where
where 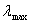 is the maximal (in absolute value) eigenvalue of the Jacobian matrix A given in section 2.6.In the first case we consider the initial data
is the maximal (in absolute value) eigenvalue of the Jacobian matrix A given in section 2.6.In the first case we consider the initial data 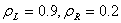
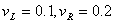 , to yield:
, to yield: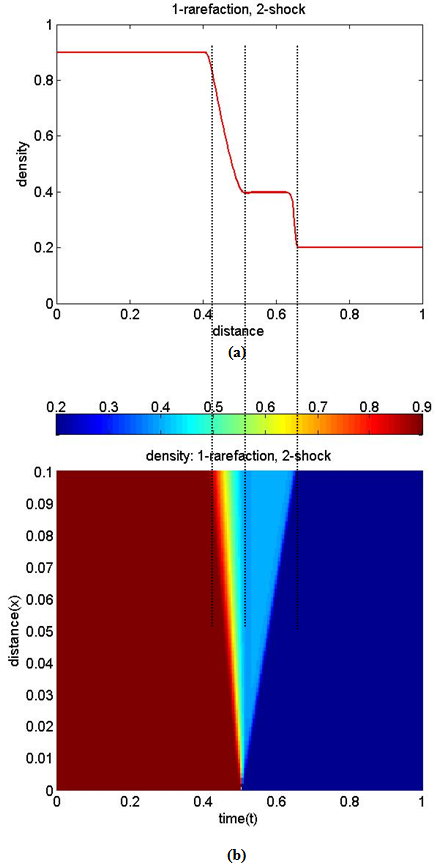 | Figure 1.1. (a). Density profile for a 1-rarefaction followed by a 2-shock, (b). distance-time graph of the density profile for a 1-rarefaction followed by a 2-shock |
In the second case we consider the initial data 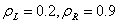
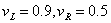 , to yield:
, to yield: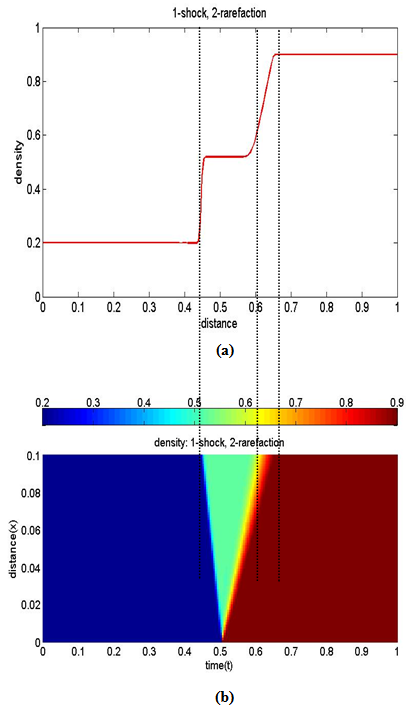 | Figure 1.2. (a). Density profile for a 1-shock followed by a 2-rarefaction, (b). distance-time graph of the density profile for a 1-shock followed by a 2-rarefaction |
6. Conclusions
Through the analysis of the Euler equation for an isothermal gas we were able to get two real and distinct eigenvalues which enabled us to determine the wave structures for the possible solutions to the Riemann problem. The analytical solutions was found by considering the Rankine-Hugoniot conditions to obtain the shock wave solution and using the fact that rarefaction waves lie on the integral curves.The numerical scheme used is found to adequately approximate the shock wave as well as the rarefaction wave as evidenced by the simulations. In these simulations, two cases have been considered. In case 1 we considered some initial data which gave rise to a 1-rarefaction followed by a 2-shock waves, while in case 2 we considered another set of initial data which gave rise to a 1-shock followed by a 2-rarefaction waves.Due to insufficient time the author of this study decided to deal with an isothermal case of the Euler equation and thus recommends for investigation of the Euler equations including the energy equation. We recommend for researchers to compare the relaxation scheme used in this research with other numerical schemes such as the Godunov scheme.One can also check the accuracy of the numerical method used in this research by comparing it with the exact solution.
ACKNOWLEDGEMENTS
The author wishes to thank Dr. Kimathi, Phineas Roy Kiogora and Nicholas M. Mutua for their input in this research. Their immense contribution in this research is highly appreciated.
References
| [1] | Eleuterio F. Toro. Riemann Solvers and Numerical Methods for Fluid Dynamic, Third edition, Springer, 2009. |
| [2] | Mengel A. (2006), “Numerical computation of the shock tube problem by means of wave digital principles,” Advances in Radio Science, Volume 4, pp 161-164. |
| [3] | Randall J. Leveque. Numerical Methods for conservation laws, BirkhauserVerlag, 1992. |
| [4] | Ravi S. (1997) “Computational methods for self similar solutions of the compressible Euler Equations,” Journal of Computational Physics, Volume 132, pp 327-345. |
| [5] | Shi Jin, Zhouping Xin (1995) “The relaxation schemes for systems of conservation laws in arbitrary space dimensions”, John Wiley & Sons, Inc. pp 235-275 |
| [6] | Sweby P.R, (1984) “High resolution schemes using flux limiters for hyperbolic conservation laws”, SIAM J. Numer. Anal, volume 21, pp 995-1011 |
| [7] | Van Leer B, (1979) “Toward the ultimate conservative difference schemes V.A second-order sequal to Godunov’s method”, J. Comput. Phys, volume 32, pp 101-136. |
| [8] | Wang Wen-Long, Li Huag and Pan Sha (2011) “Performance Comparison and Analysis of Different Schemes and Limiters,” World Academy of Science, Engineering and Technology, Volume 79. |

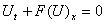
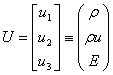 ,
, 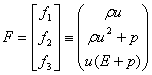 Where
Where 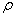 is density, p is pressure, u is the particle velocity and E is the total energy per unit volume.Under the assumption that the entropy, s, is a constant everywhere, which is a simplification of the thermodynamics. Now the EOS is
is density, p is pressure, u is the particle velocity and E is the total energy per unit volume.Under the assumption that the entropy, s, is a constant everywhere, which is a simplification of the thermodynamics. Now the EOS is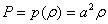
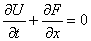
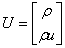
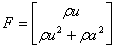 Thus we have,
Thus we have,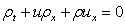
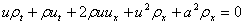
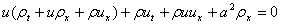 , thus the two equations can be written as:
, thus the two equations can be written as: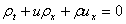 ,
,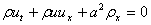 which can be written in matrix form as:
which can be written in matrix form as: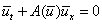 Where
Where 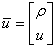 ,
, 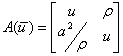 Now to get the eigenvalues for the matrix
Now to get the eigenvalues for the matrix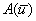 , we use the manipulation
, we use the manipulation 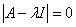
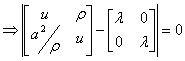 , which gives rise to a quadratic equation with real roots
, which gives rise to a quadratic equation with real roots 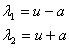
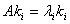 where
where 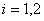 Thus using the first eigenvalue,
Thus using the first eigenvalue, 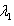 , we have:
, we have: 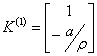 , as the corresponding eigenvector, while using the second eigenvalues,
, as the corresponding eigenvector, while using the second eigenvalues, 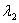 , we have:
, we have: 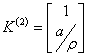 as the corresponding eigenvector.From the above eigenvalues and eigenvectors then we can be able to determine the structure of the waves that is by considering the Riemann’s problem defined by
as the corresponding eigenvector.From the above eigenvalues and eigenvectors then we can be able to determine the structure of the waves that is by considering the Riemann’s problem defined by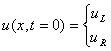
 The solution to this problem depends on the relative values of
The solution to this problem depends on the relative values of  and
and 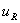 . That is, for
. That is, for 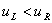 , a rarefaction wave is going to develop while for
, a rarefaction wave is going to develop while for 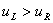 , a shock wave is going to appear. Thus for a case where no vacuum is present the exact solutions will have the two different waves which would be associated with the eigenvalues 2.6.
, a shock wave is going to appear. Thus for a case where no vacuum is present the exact solutions will have the two different waves which would be associated with the eigenvalues 2.6.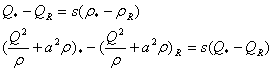 This gives two equations with three unknowns, that is,
This gives two equations with three unknowns, that is, 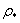 ,
, 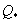 and s, which can easily be solved for
and s, which can easily be solved for 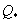 and s in terms of
and s in terms of 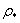 , Leveque[3]
, Leveque[3]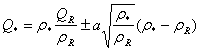
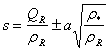
 . For instance, in Leveque[3], we parametize the curves by taking
. For instance, in Leveque[3], we parametize the curves by taking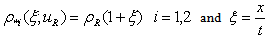 We then have
We then have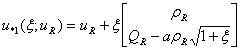 ,
,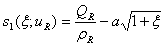 and
and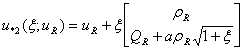 ,
,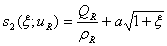 Also the rarefaction wave solution takes the form
Also the rarefaction wave solution takes the form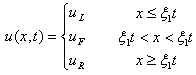 Since the rarefactions lie along the integral curve, Leveque[3], we consider the following equation.
Since the rarefactions lie along the integral curve, Leveque[3], we consider the following equation.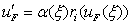 Where
Where 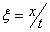 ,
, 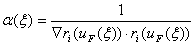
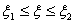 Therefore,
Therefore,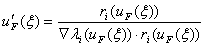
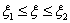 With initial data
With initial data 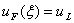 , where
, where 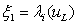 and
and 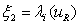 Now, using the first eigenvalue and equation 3.1, we can be able to construct the 1-rarefactions for the equations, thus the system of ODE’s takes the form
Now, using the first eigenvalue and equation 3.1, we can be able to construct the 1-rarefactions for the equations, thus the system of ODE’s takes the form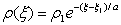
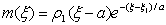 Where on eliminating
Where on eliminating 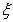 to solve for m as a function of
to solve for m as a function of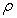 , we have
, we have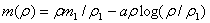
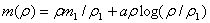
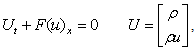
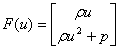 With initial data
With initial data 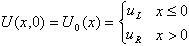 Now introducing the relaxation system, we have
Now introducing the relaxation system, we have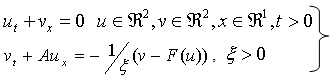
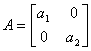 , is a positive diagonal matrix to be chosen.For
, is a positive diagonal matrix to be chosen.For 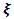 sufficiently small, it is expected that by solving (4.1) properly, one can obtain good approximations to the original conservation lawsThe positive constant a need satisfy: Shi J. et a l [5],
sufficiently small, it is expected that by solving (4.1) properly, one can obtain good approximations to the original conservation lawsThe positive constant a need satisfy: Shi J. et a l [5], 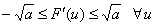 For the relaxation system (4.1), the initial data is:
For the relaxation system (4.1), the initial data is: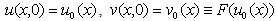 , Now introducing the spatial grid points
, Now introducing the spatial grid points 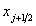 with mesh width
with mesh width 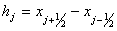 while the discrete time level
while the discrete time level 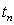 are spaced uniformly with space step
are spaced uniformly with space step 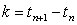 for n=0, 1, 2.Here we denote by
for n=0, 1, 2.Here we denote by 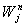 the approximate cell average of a quantity W in the cell
the approximate cell average of a quantity W in the cell 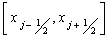 at time
at time 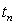 and by
and by 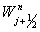 the approximate point value of W at
the approximate point value of W at  and
and 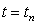 .A spatial discretization to equation 4.1 in conservation form can be written as:
.A spatial discretization to equation 4.1 in conservation form can be written as: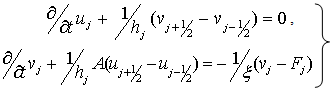
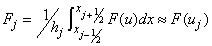 Since the relaxation system 4.1 has two characteristic variables, see Shi J. et al 5,
Since the relaxation system 4.1 has two characteristic variables, see Shi J. et al 5,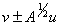
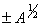 respectively.For better accuracy we use a second-order scheme that is the Van Leer’s MUSCL scheme, see Van Leer[7].Applying this scheme to the pth component that is equation 4.3, gives
respectively.For better accuracy we use a second-order scheme that is the Van Leer’s MUSCL scheme, see Van Leer[7].Applying this scheme to the pth component that is equation 4.3, gives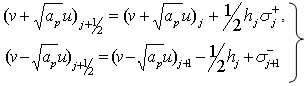
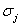 is the slope of
is the slope of 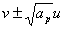 on the j-th cell which we define using Sweby’s notation, see Sweby[6].
on the j-th cell which we define using Sweby’s notation, see Sweby[6].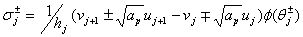 ,
,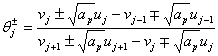 Where
Where 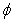 is a slope-limiter function given as, Van Leer[7]
is a slope-limiter function given as, Van Leer[7]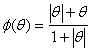 Solving equations 4.4 for
Solving equations 4.4 for 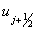 and
and 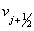 gives
gives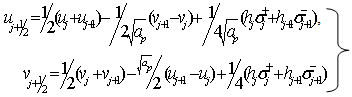
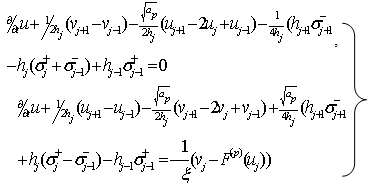
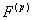 is the p-th component of F.Since the one dimensional Euler equation 2.3 has two eigen values
is the p-th component of F.Since the one dimensional Euler equation 2.3 has two eigen values 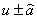 we take
we take 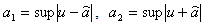 , Now, to obtain the time discretization for the relaxation scheme we use a second-order TVD Runge-Kutta splitting scheme which was introduced by Jin, Shi J. et al[5]Denote
, Now, to obtain the time discretization for the relaxation scheme we use a second-order TVD Runge-Kutta splitting scheme which was introduced by Jin, Shi J. et al[5]Denote 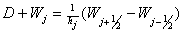 Then applying the second-order TVD Runge-Kutta splitting scheme to the time derivative in 4.6, that is applying it to 4.1 yields
Then applying the second-order TVD Runge-Kutta splitting scheme to the time derivative in 4.6, that is applying it to 4.1 yields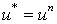 ,
,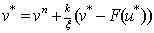 ;
;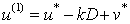 ,
,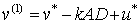 ;
;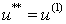 ,
,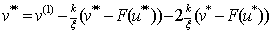 ;
;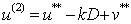 ,
,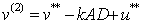 ;
;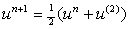 ,
,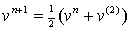 ;
;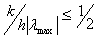 where
where 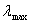 is the maximal (in absolute value) eigenvalue of the Jacobian matrix A given in section 2.6.In the first case we consider the initial data
is the maximal (in absolute value) eigenvalue of the Jacobian matrix A given in section 2.6.In the first case we consider the initial data 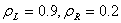
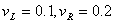 , to yield:
, to yield:
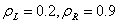
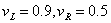 , to yield:
, to yield:
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML