Ogbogbo G. O.1, Ebuh G. U2, Aronu C. O.2
1Department of statistics Delta State Polytechnic, Otefe-Oghara, Nigeria
2Department of statistics Nnamdi Azikiwe University, Awka, Nigeria
Correspondence to: Aronu C. O., Department of statistics Nnamdi Azikiwe University, Awka, Nigeria.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
This study examined the transition into various grade levels of academic staff at Delta State Polytechnic, Otefe-Oghara using a markov chain approach. The staff transition for the various grade levels were found to be stationarity, since the 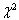 (computed) was obtained as 16.12 with a corresponding p-value = 0.1925 which fall on the acceptance region using
(computed) was obtained as 16.12 with a corresponding p-value = 0.1925 which fall on the acceptance region using 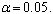 It was found that an entrant on grade 1 (Assistant lecturer grade) is expected to stay for a period of 2 years and seven months in grade 1; an entrant on grade 2 (Lecturer III) is expected to stay for a period of 4 years and a month in grade 2; an entrant on grade 3 (Lecturer II) is expected to stay for a period of 3 years and 2 months in grade 3; an entrant on grade 4 (Lecturer I) is expected to stay for a period of 3 years and 4 months; an entrant on grade 5 (Senior Lecturer) is expected to stay for a period of 2 years and 11 months; an entrant on grade 6 (Principal Lecturer) is expected to stay for a period of 2 years and six months in grade 6; an entrant on grade 7 (Chief Lecturer) is expected to stay for a period of 4 years and 3 months in grade 7. It was concluded that staff in Principal Lecturer (grade 6) and Assistant Lecturer (grade 1) has less expected length of stay and also has greater chance of promotion than other grade level, hence, potential applicants are advised to apply for Principal Lecturer and Assistant Lecturer positions if vacancies exist in the Institution.
It was found that an entrant on grade 1 (Assistant lecturer grade) is expected to stay for a period of 2 years and seven months in grade 1; an entrant on grade 2 (Lecturer III) is expected to stay for a period of 4 years and a month in grade 2; an entrant on grade 3 (Lecturer II) is expected to stay for a period of 3 years and 2 months in grade 3; an entrant on grade 4 (Lecturer I) is expected to stay for a period of 3 years and 4 months; an entrant on grade 5 (Senior Lecturer) is expected to stay for a period of 2 years and 11 months; an entrant on grade 6 (Principal Lecturer) is expected to stay for a period of 2 years and six months in grade 6; an entrant on grade 7 (Chief Lecturer) is expected to stay for a period of 4 years and 3 months in grade 7. It was concluded that staff in Principal Lecturer (grade 6) and Assistant Lecturer (grade 1) has less expected length of stay and also has greater chance of promotion than other grade level, hence, potential applicants are advised to apply for Principal Lecturer and Assistant Lecturer positions if vacancies exist in the Institution.
Keywords:
Lecturer,Transition, Academic Staff, Stationarity, Carer Prospect, Matrix
Cite this paper: Ogbogbo G. O., Ebuh G. U, Aronu C. O., Determining the Expected Length of Stay of Academic Staff in Various Grade Levels in a Polytechnic Institution in Nigeria Using a Markov Chain Approach, American Journal of Computational and Applied Mathematics , Vol. 3 No. 4, 2013, pp. 225-232. doi: 10.5923/j.ajcam.20130304.05.
1. Introduction
Organisations tend to be hierarchical with finite number of levels (ranks). Humans are considered as the most crucial and potentially unpredicted resource which an organisation utilises to achieve it set goals. If an organisation fails to place and direct human resources in the right areas of business, at the right time, and at the right cost, serious inefficiencies are likely to occur creating considerable operational difficulties or even business failure. In order to achieve efficiency in managing human resources in an organisation, the coordination of demand and supply is required, together with the monitoring and assessment of productivity and technological changes. Career pattern is concerned with the passage of individuals through an organizational system. That is, the duration of individuals progress through the grades in an organization. It is clear that it is difficult to track and monitor this progress of the individuals through the organizations grades without the complexity of qualitative factors and the projection of resource mismatches[1].[2], recognised that ‘shortages’ of persons with critical skills and knowledge required for effective national development is a serious problem in most developing nations. This problem is further compounded by some derogatory and discriminatory policies (in Nigeria for instance) like “state of origin”, “federal character”, etcetera.[3] in his study stressed that analysis of manpower systems have become very important component of planned economic development of any organisation or nation. However, manpower planning depends on the highly unpredictable human behaviour and uncertain social environment in which the system functions. He added that this implies that probabilistic or stochastic models of manpower systems are very much essential in management of any organisation. The present study was motivated out of curiosity and arguments by most academic staff of Delta State Polytechnic Otefe-Oghara who claims that promotion has been overlooked by the management of the Institution. Therefore the need to determine the length of stay of academic staff in various grade levels of the Institution and ascertaining the chances of promotion in various grade levels a sine qua non.
1.1. Manpower Models
Traditionally, manpower models were thought as mathematical representations of a manpower system. The representations are usually in the form of mathematical equations, which expresses the manpower process.[4], explained that manpower systems are normally considered as complex systems in which their counter parts interacts with each other in order to accomplish the desired outcome. Subsystems can be identified which makes it necessary to distinguish between the system by age, length of services or by department and section. Manpower planning is the process of ensuring that the correct number of human resources is available at the right time at the right place. In order to do that they need appropriate analytical tools, much effort has been devoted to developing tools and techniques to assist managers with their planning. Many of these were based on the theory of stochastic processes and more specifically the concept of Markov chains[5]. Defining Human resources[6], stated that human resources constitute the ultimate basis for wealth of nations, capital and natural resources are passive factors of production; human beings are the active agents who accumulate capital, exploit natural resources, build social, economic and political organizations, and carry forward national development. Clearly, a country which is unable to develop the skills and knowledge of its people and to utilize them effectively in the national economy will be unable to develop anything else.[7], carried out a study on the theoretical markov chain model for evaluating correctional methods applied to people with criminal tendencies. He used markov chain approach which uses past history to predict the state of a system in the future and came out with a model which comprises the effect of different correctional practices on people with criminal tendencies.[8], focused on tandem queues. They considered a discrete-time tandem queue with blocking. In general, computing the response time in this type of queues requires setting up Markov chain, finding its stationary values and then the response time. In their study they directly based the Markov chain regarding to the age of the leading job in the first queue which led them to calculate the response time easily from the stationary values of this Markov chain.[9], in their study developed a model for manpower management. Their model explicitly considered the fact that managers classify employees into good and poor performers, that certain sources of new employees are more likely to produce good performers than others and that there is a period of learning before a person reaches his full potential in a job. Numerical examples of the use of the model were presented, first to determine the pattern of recruitment from various sources, given manning requirements, that maximizes a measure of performance of the department considered in their study. Next, some of the parameters of the model were varied to determine the effect of changes in turnover rate and rate of promotion to higher job levels. The model presented is descriptive of the movement of individuals through an organization. It does not attempt to explain why people leave an organization or why they join it in the first place.
1.2. Markov and Renewal Manpower Models
Markov models start with a given group of employees that exist in a level of the organisation; given the flows in and out of each level (i.e. recruitment and promotions from outside the system together with wastage) they estimate the population of the level in the future. This type of model is particularly useful when the knowledge of existing employees are available together with the probabilities of flows between succeeding years and the required future manpower is not known. Markov models are based on the assumption that future employees in any level of the organisation are determined not so much by the number required in that level of the organisation but by the promotions and recruitment encouraging the movement up through the system. Because of this characteristic of “pushing” Markov models are often called “push” models. Renewal models concentrate on the basic assumption that requirements are met by changes in promotions and recruitment rates. Knowing the manpower requirements what is required is knowledge of how much recruitment and how many promotions should take place to satisfy them. In this way employees are “pulled” through the system to meet predetermined requirements of the system. Equally, because of this, renewal models are often called “pull” models. Applying the manpower method in an organisation with grades, a staff member can join the grades with equal probability and the entry into the system at the grade is independent of what happens at lower grades within the system, a staff member can be promoted to the next higher grade, stay in the present grade or leave the system by dismissal, retirement, death or for whatever reason each year. These modes of withdrawal will be pooled together. Manpower systems are hierarchical in structure. In a polytechnic institution where the cadre ranges from assistant lecturer to chief lecturer; every staff aspires to reach the top but not all get to the top. The career progress of staff depends mostly on qualification, years of experience and academic productivity in terms of proof of continued research and additional publication.
2. Materials and Methodology
2.1. Markov Chain
A Markov process 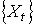 is a stochastic process with the property that, given the value of
is a stochastic process with the property that, given the value of 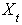 the values of
the values of 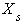 , for
, for 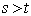 are not influenced by the values of
are not influenced by the values of 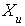 for
for 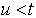 . In other words, the probability of any particular future behaviour of the process, when its current state is known exactly, is not altered by additional knowledge concerning its past behaviour[10]. A discrete-time Markov chain is a Markov process whose state space is a finite or countable set, and whose (time) index set is T = (0, 1, 2, ...). In formal terms, the Markov property is that
. In other words, the probability of any particular future behaviour of the process, when its current state is known exactly, is not altered by additional knowledge concerning its past behaviour[10]. A discrete-time Markov chain is a Markov process whose state space is a finite or countable set, and whose (time) index set is T = (0, 1, 2, ...). In formal terms, the Markov property is that 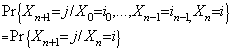 | (1) |
For all time points n and all states 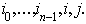 It is frequently convenient to label the state space of the Markov chain by the nonnegative integers {0, 1, 2, ...}, which will is often used unless the contrary is explicitly stated. It is customary to speak of
It is frequently convenient to label the state space of the Markov chain by the nonnegative integers {0, 1, 2, ...}, which will is often used unless the contrary is explicitly stated. It is customary to speak of 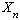 as being in state
as being in state 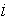 if
if 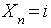 .The probability of the system
.The probability of the system 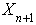 being in state
being in state 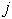 given that
given that 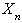 is in state
is in state 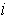 is called the one – step transition probability and is denoted by
is called the one – step transition probability and is denoted by 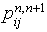 . That is
. That is 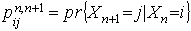 | (2) |
Let i= 1, 2, 3, 4, 6, 7; represent the cadre ranging from Assistant lecturer (1), Lecturer III (2), Lecturer II (3), Lecturer I (4), Senior Lecturer (5), Principal Lecturer (6) and chief lecturer (7).Where t= 1, 2, 3, 4, 5, 6 represent the academic sessions of the Institution; t =1 stands for 2006/07 session, t =2 stands for 2007/08 session, t =3 stands for 2008/09 session, t =4 stands for 2009/10 session, t =5 stands for 2010/11 and t =6 stand for 2011/2012 session.The following notations and assumptions are relevant;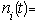 Number of staff in cadre
Number of staff in cadre 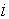 at the beginning of the
at the beginning of the 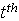 session
session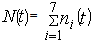 the total size of staff at the beginning of the
the total size of staff at the beginning of the 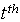 session
session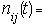 Number of persons who move from grade
Number of persons who move from grade 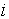 to
to 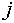 at
at 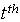 session
session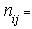 The wastage flow from
The wastage flow from 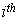 cadre within the
cadre within the 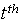 session
session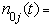 The recruitment flow to grade
The recruitment flow to grade 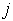 at the beginning of the
at the beginning of the 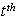 session
session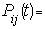 The transition probability of a person in grade
The transition probability of a person in grade 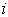 moving to grade
moving to grade 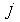 within the
within the 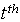 session
session 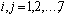
2.2. Model Assumption
The following assumptions are made about the recruitment and promotion flow and the transition Probability Matrices (TPMS) denoted by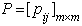 ; where m denotes the cadres.a. Recruitment can be made into any of the grades and at the beginning of any session where
; where m denotes the cadres.a. Recruitment can be made into any of the grades and at the beginning of any session where 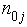 represents the recruitment flow and
represents the recruitment flow and 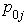 the probability of recruitment such that
the probability of recruitment such that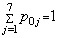 | (3) |
b. Promotions in the institution depends on such factors as the qualification experience and productivity of staff but due to individual differences, the promotion flow 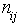 is a random variable with independent transition probability
is a random variable with independent transition probability 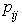 for which summing over
for which summing over 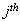 rows will give ;
rows will give ;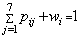 | (4) |
c. The assumption of an orderly and stable flow would imply that the initial transition probability 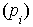 as well as the overall TPM (Transition Probability Matrix)
as well as the overall TPM (Transition Probability Matrix) 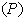 is stationary overtime which implies that the probability matrix is independent of time.
is stationary overtime which implies that the probability matrix is independent of time.
2.3. Determination of Transition Probabilities
The statistical inference procedures for markov chains following the (see[11]) and using the principle of maximum likelihood to exploit the multinomial distribution of 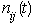 given
given 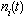 for each period with probabilities
for each period with probabilities 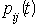 gives the estimates of
gives the estimates of 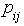 as
as 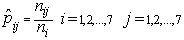 | (5) |
If stationarity holds, the pooled estimate becomes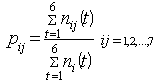 | (6) |
Speaking on the substochastic nature of the transition probability matrix,[12] using the markov chain to model the manpower of Solvenian Armed Forces explained that the actual model used in their study was based on the model described in ([13]), where a vector of recruit’s r was added. The model allows wastage w; which accounts for those people who leave the system. They argued that in their model, the transition matrix P need not be stochastic but only substochastic, which implies that the sum of rows of the transition matrix may be less than 1, where the difference is wastage w, thus,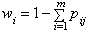 .
.
2.4. Stationarity of Transition Probabilities
[14] stated that the transition probabilities may or may not be constant over time. Hence, in stochastic process, if the transition probabilities over the period of study are not constant, the procedure will be to estimate a different transition probability matrix for each transition ([15];[16]).Assumption of constant transition probabilities overtime implies that 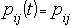 for all
for all 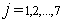 Our test hypothesis is stated as;
Our test hypothesis is stated as;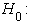 Transition probabilities are constant overtime
Transition probabilities are constant overtime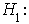 Transition probabilities are not constant overtimeTo test the stationarity of the seasonal TPM’s
Transition probabilities are not constant overtimeTo test the stationarity of the seasonal TPM’s 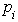 with elements
with elements 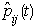 we use the following layout below.
we use the following layout below. 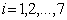 The
The 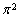 - test of stationarity specify that1. Transitions from row state
- test of stationarity specify that1. Transitions from row state 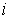 to state
to state 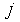 are stationary at
are stationary at 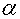 - level of significance if
- level of significance if 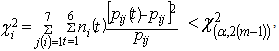 | (7) |
Where m is the number of 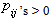 2. The entire TPM, P is constant overtime if
2. The entire TPM, P is constant overtime if 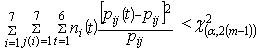 | (8) |
Where m is the number of 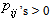 .
.
2.5. The Career Prospects of Staff
It should also be of interest to have an idea of the expected length of time a lecturer is likely to spend in a period and also the mean length of stay, which is the time spent in Delta State Polytechnic.[13] established that the mean length of time spent in grade 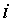 given entry in grade
given entry in grade 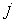 is given by
is given by 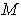 and the probability of attainment of grade
and the probability of attainment of grade 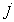 from grade
from grade 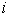 is given by
is given by 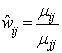 | (9) |
Where 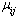 and
and 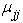 are element of the fundamental matrix
are element of the fundamental matrix 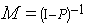 | (10) |
Where P is the (7 X 7) TPM andis the identity matrix.
2.6. Data Collection
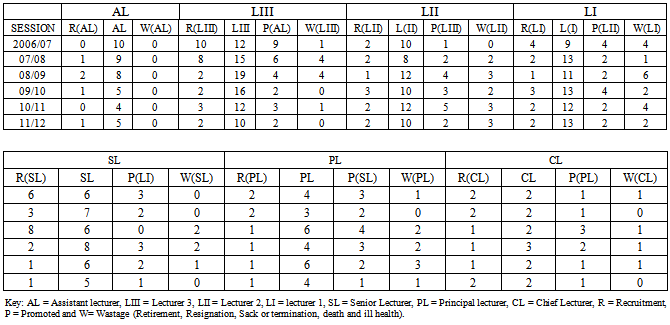
The data used in this study is secondary data obtained from the Personnel Department of Delta State Polytechnic, Oghara for 2006/07 – 2011/12 sessions. The manpower data of the academic staff of Delta state polytechnic, Oghara is presented in Table 1; where the grade level of staff is classified into Grade1 – Assistant lecturer, Grade2 – lecturer III, Grade3 – lecturer II, Grade4 – lecturer I, Grade5 – senior lecturer, Grade6 – principal lecturer, Grade7 – chief lecturer.Table 1. Distribution of Manpower Structure of Delta State Polytechnic Otefe-Oghara
 |
| |
|
3. Data Analysis
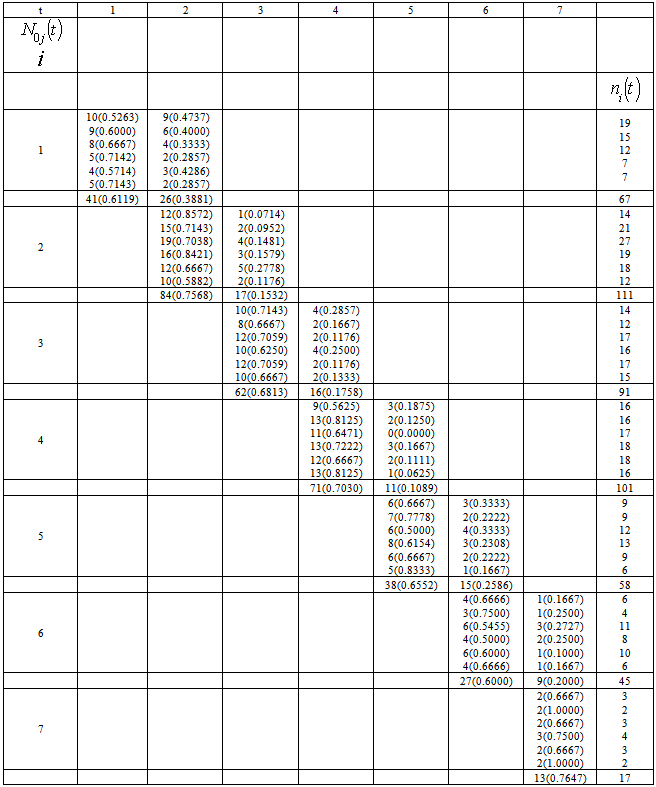
Using the collected data as presented in Table 1 the transition probability of the academic staff of Delta State polytechnic was summarized for the seven grade levels below (see Table 2).Table 2. Transition of Academic Staff into various Grades in Delta State Polytechnic for t =1, 2, 3, 4, 5, 6
 |
| |
|
From Table 2, the transition probability matrix for the staff transition was extracted as given 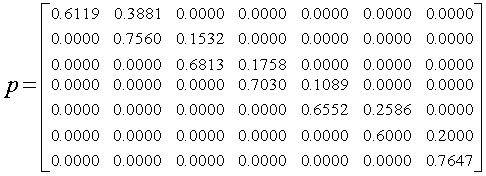
3.1. Stationarity of the Transition Probabilities
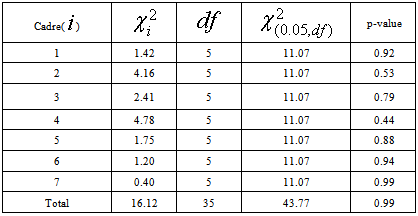
The transition probabilities for the various grade levels presented in Table 2 was tested for stationarity using the procedure discussed in section 2.4 (see Equation 7 and Equation 8). Table 3. Summary Result of Test of stationarity of Transition probabilities
 |
| |
|
Recall that the Chi-square used as the test statistics for TPM is 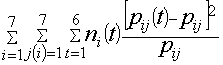 = 16.12Since, the p-value = 0.99 is greater than the
= 16.12Since, the p-value = 0.99 is greater than the 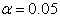 , we accept the null hypothesis of stationarity of the cadre transition.
, we accept the null hypothesis of stationarity of the cadre transition.
3.2. Expected Length of Stay in a Grade
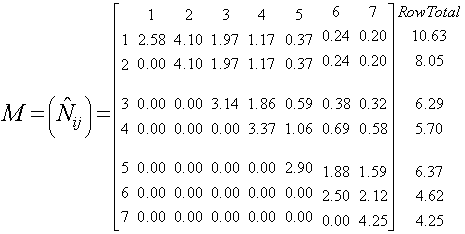
It should also be of interest to have an idea of the expected length of time a staff is likely to spend in a period and also the percentage chance of promotion in the various grade levels. The fundamental matrix was obtained using Equation 9 and Equation 10 as discussed in section 2.5.Fundamental Matrix of the grade level of Delta State Polytechnic, Oghara

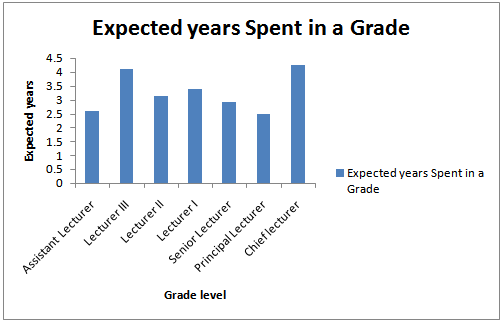 | Figure 1. Distribution of Expected years Spent in a Grade |
4. Discussion
From the result of the stationarity test, it was observed that the grade transition flows from one grade to the other is stationary, since, the p-value = 0.99 is greater than the 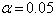 , we accept the null hypothesis of stationarity of the grade transition (see Table 3). We can denote from the result of the fundamental matrix (M) that an entrant on grade 1 (Assistant lecturer grade) is expected to stay for a period of 2 years and seven months in grade 1; an entrant on grade 2 (Lecturer III) is expected to stay for a period of 4 years and a month in grade 2; an entrant on grade 3 (Lecturer II) is expected to stay for a period of 3 years and 2 months in grade 3; an entrant on grade 4 (Lecturer I) is expected to stay for a period of 3 years and 4 months; an entrant on grade 5 (Senior Lecturer) is expected to stay for a period of 2 years and 11 months; an entrant on grade 6 (Principal Lecturer) is expected to stay for a period of 2 years and six months in grade 6; an entrant on grade 7 (Chief Lecturer) is expected to stay for a period of 4 years and 3 months in grade 7. Also, the career prospect analysis, the matrix
, we accept the null hypothesis of stationarity of the grade transition (see Table 3). We can denote from the result of the fundamental matrix (M) that an entrant on grade 1 (Assistant lecturer grade) is expected to stay for a period of 2 years and seven months in grade 1; an entrant on grade 2 (Lecturer III) is expected to stay for a period of 4 years and a month in grade 2; an entrant on grade 3 (Lecturer II) is expected to stay for a period of 3 years and 2 months in grade 3; an entrant on grade 4 (Lecturer I) is expected to stay for a period of 3 years and 4 months; an entrant on grade 5 (Senior Lecturer) is expected to stay for a period of 2 years and 11 months; an entrant on grade 6 (Principal Lecturer) is expected to stay for a period of 2 years and six months in grade 6; an entrant on grade 7 (Chief Lecturer) is expected to stay for a period of 4 years and 3 months in grade 7. Also, the career prospect analysis, the matrix 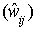 obtained showed that on the average potential entrants in grade 1 and 2 have 63% and 63% chances of being promoted to Lecturer II, entrant in grade3 have 55% chances of being promoted to Lecturer I, entrant in grade 4 have about 37% chance of being promoted to Senior Lecturer while entrants in grade 5 have about 75% chance of being promoted to Principal Lecturer and entrants in grade 6 have about 50% chance of being promoted to Chief Lecturer.From the graphical representation (see Figure 1) we observed that entrant into Principal Lecturer grade and Assistant Lecturer grade are expected to spend less years than the other grade levels with an expected length of 2 years and 6 months and 2 years and 7 months respectively.
obtained showed that on the average potential entrants in grade 1 and 2 have 63% and 63% chances of being promoted to Lecturer II, entrant in grade3 have 55% chances of being promoted to Lecturer I, entrant in grade 4 have about 37% chance of being promoted to Senior Lecturer while entrants in grade 5 have about 75% chance of being promoted to Principal Lecturer and entrants in grade 6 have about 50% chance of being promoted to Chief Lecturer.From the graphical representation (see Figure 1) we observed that entrant into Principal Lecturer grade and Assistant Lecturer grade are expected to spend less years than the other grade levels with an expected length of 2 years and 6 months and 2 years and 7 months respectively.
5. Conclusions
In this study makovian approach was used to determine the transition of academic staff in the various grade levels in Delta state polytechnic Otefe – Oghara between 2006/07 and 2011/12 academic session. The findings showed that the grade transition flow is stationary over the observed time period and also found that staff in grade 6 (Principal Lecturer) have greater percentage chance (73%) of being promoted to grade 7 (Chief lecturer) followed by staff in grade 1 (Assistant Lecturer) and grade 2(Lecturer III) with 60% chance of being promoted to grade 2 (Lecturer III) and grade 3 (Lecturer II) respectively. While staff in grade 3 (Lecturer II) have 58% chance of being promoted to grade 4 (Lecturer I) in the institution. Since it was obtained that staff in Principal Lecturer (grade 6) and Assistant Lecturer (grade 1) has less expected length of stay and also has greater chance of promotion than other grade level, hence, potential applicants are advised to apply for Principal Lecturer and Assistant Lecturer positions if vacancies exist in the Institution. However, this study presents the academic structure of Delta state Polytechnic Otefe–Oghara. We recommend for future research a manpower structure modelling for administrative staff of Delta state Polytechnic Otefe – Oghara from the inception of the institution to date.
References
| [1] | Obaji, V., and Okafor, F.C. (2012). Two Term Mixed Exponential Distribution in Non Homogeneous Manpower System, Journal of the Nigeria Statistical Association (JNSA), Vol. 24; 85 – 92. |
| [2] | Harbison, F. (1968),.“A System Analysis Approach to Human Resources Development Planning” In: Coombs, P.H. (Ed), Manpower Aspects of Educational Planning. UNESCO, IIEP; Paris. Pp. 7 - 9. |
| [3] | Setlhare, K. (2009). Modeling of an Intermittently Busy manpower System. Proceedings of IASTED Conference, September 11-13, Gaborne – Bostwana. |
| [4] | Khnoog, C.M. (1996). An Integrated System Framework and Analysis Methodology for Manpower Planning. International Journal of Manpower Vol. 17, Pp. 26 – 46. |
| [5] | Bowel, A. (1974), A Guide to Manpower Planning. The Macmillan Press Ltd, London. |
| [6] | Harbison F. (1973), Human Resources as the Wealth of Nations. Oxford University Press, New York. |
| [7] | Chukwu, W. I. E., (1999), A Theoretical Markov Chain Model for Evaluating Correlational Method Applied to People with Criminal Tendencies. A paper presented to the Department of Statistics University of Swaziland Southern Africa during their Statistical week. |
| [8] | Van Houdt, B. and Alfa, A.S. (2005), Response Time in a Tandem Queue with Blocking, Markovian Arrivals and Phase-Type Services. Operations Research Letters, 33, pp. 373-381. |
| [9] | Lilien, L. G. and Rao, A. G. (1975), A Model for Manpower Management. Institute of Management Sciences, Vol. 21. No. 12, Pp. 1447-1457. |
| [10] | Taylor H. M. and Karlin S. (1998., An Introduction to Stochastic Modeling (Third Edition), Academic Press limited, London, pages 95 – 417. |
| [11] | Bhat, U.N. (1971). Elements of Applied Stochastic Process. John Wiley and Sons, New York, pages 56-120. |
| [12] | Škulj, D., Vehovar, V., and Štamfelj, D. (2008). The Modelling of Manpower by Markov Chains – A Case Study of the Slovenian Armed Forces, Informatica 32, 289–291. |
| [13] | Bartholomew, D.J., Forbes, A.F., and McClean, S.I. (1991). Statistical Techniques for Manpower Planning, John Wiley & Sons, Pages 14-22 |
| [14] | Uche, P.I. (1978). On Stochastic Models for Educational Planning, International Journal of Math ed. Science Tech. 9, No. 3, pp. 333 – 342. |
| [15] | Golan, A., and Vogel, S. J. (2000). Estimation of Non–stationary Social Accounting Matrix Coefficients with Supply Side Information, Economic Systems Research, 12. |
| [16] | Karantininis, K. (2001), Information Based Estimates for the Non-Stationary Transition Probability Matrix: An Application to the Danish Pork Industry, Unit of Economics Working Papers (1): 1-23. |

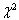 (computed) was obtained as 16.12 with a corresponding p-value = 0.1925 which fall on the acceptance region using
(computed) was obtained as 16.12 with a corresponding p-value = 0.1925 which fall on the acceptance region using 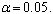 It was found that an entrant on grade 1 (Assistant lecturer grade) is expected to stay for a period of 2 years and seven months in grade 1; an entrant on grade 2 (Lecturer III) is expected to stay for a period of 4 years and a month in grade 2; an entrant on grade 3 (Lecturer II) is expected to stay for a period of 3 years and 2 months in grade 3; an entrant on grade 4 (Lecturer I) is expected to stay for a period of 3 years and 4 months; an entrant on grade 5 (Senior Lecturer) is expected to stay for a period of 2 years and 11 months; an entrant on grade 6 (Principal Lecturer) is expected to stay for a period of 2 years and six months in grade 6; an entrant on grade 7 (Chief Lecturer) is expected to stay for a period of 4 years and 3 months in grade 7. It was concluded that staff in Principal Lecturer (grade 6) and Assistant Lecturer (grade 1) has less expected length of stay and also has greater chance of promotion than other grade level, hence, potential applicants are advised to apply for Principal Lecturer and Assistant Lecturer positions if vacancies exist in the Institution.
It was found that an entrant on grade 1 (Assistant lecturer grade) is expected to stay for a period of 2 years and seven months in grade 1; an entrant on grade 2 (Lecturer III) is expected to stay for a period of 4 years and a month in grade 2; an entrant on grade 3 (Lecturer II) is expected to stay for a period of 3 years and 2 months in grade 3; an entrant on grade 4 (Lecturer I) is expected to stay for a period of 3 years and 4 months; an entrant on grade 5 (Senior Lecturer) is expected to stay for a period of 2 years and 11 months; an entrant on grade 6 (Principal Lecturer) is expected to stay for a period of 2 years and six months in grade 6; an entrant on grade 7 (Chief Lecturer) is expected to stay for a period of 4 years and 3 months in grade 7. It was concluded that staff in Principal Lecturer (grade 6) and Assistant Lecturer (grade 1) has less expected length of stay and also has greater chance of promotion than other grade level, hence, potential applicants are advised to apply for Principal Lecturer and Assistant Lecturer positions if vacancies exist in the Institution.
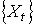 is a stochastic process with the property that, given the value of
is a stochastic process with the property that, given the value of 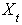 the values of
the values of 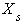 , for
, for 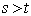 are not influenced by the values of
are not influenced by the values of 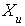 for
for 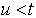 . In other words, the probability of any particular future behaviour of the process, when its current state is known exactly, is not altered by additional knowledge concerning its past behaviour[10]. A discrete-time Markov chain is a Markov process whose state space is a finite or countable set, and whose (time) index set is T = (0, 1, 2, ...). In formal terms, the Markov property is that
. In other words, the probability of any particular future behaviour of the process, when its current state is known exactly, is not altered by additional knowledge concerning its past behaviour[10]. A discrete-time Markov chain is a Markov process whose state space is a finite or countable set, and whose (time) index set is T = (0, 1, 2, ...). In formal terms, the Markov property is that 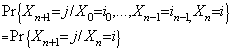
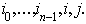 It is frequently convenient to label the state space of the Markov chain by the nonnegative integers {0, 1, 2, ...}, which will is often used unless the contrary is explicitly stated. It is customary to speak of
It is frequently convenient to label the state space of the Markov chain by the nonnegative integers {0, 1, 2, ...}, which will is often used unless the contrary is explicitly stated. It is customary to speak of 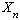 as being in state
as being in state 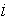 if
if 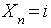 .The probability of the system
.The probability of the system 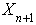 being in state
being in state 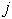 given that
given that 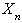 is in state
is in state 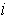 is called the one – step transition probability and is denoted by
is called the one – step transition probability and is denoted by 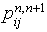 . That is
. That is 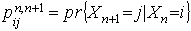
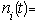 Number of staff in cadre
Number of staff in cadre 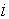 at the beginning of the
at the beginning of the 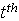 session
session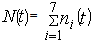 the total size of staff at the beginning of the
the total size of staff at the beginning of the 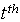 session
session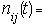 Number of persons who move from grade
Number of persons who move from grade 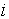 to
to 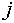 at
at 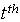 session
session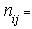 The wastage flow from
The wastage flow from 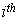 cadre within the
cadre within the 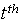 session
session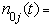 The recruitment flow to grade
The recruitment flow to grade 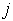 at the beginning of the
at the beginning of the 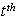 session
session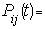 The transition probability of a person in grade
The transition probability of a person in grade 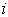 moving to grade
moving to grade 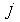 within the
within the 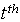 session
session 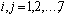
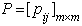 ; where m denotes the cadres.a. Recruitment can be made into any of the grades and at the beginning of any session where
; where m denotes the cadres.a. Recruitment can be made into any of the grades and at the beginning of any session where 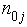 represents the recruitment flow and
represents the recruitment flow and 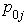 the probability of recruitment such that
the probability of recruitment such that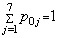
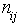 is a random variable with independent transition probability
is a random variable with independent transition probability 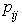 for which summing over
for which summing over 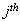 rows will give ;
rows will give ;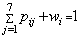
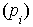 as well as the overall TPM (Transition Probability Matrix)
as well as the overall TPM (Transition Probability Matrix) 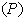 is stationary overtime which implies that the probability matrix is independent of time.
is stationary overtime which implies that the probability matrix is independent of time.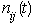 given
given 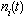 for each period with probabilities
for each period with probabilities 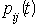 gives the estimates of
gives the estimates of 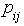 as
as 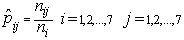
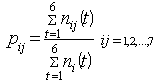
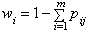 .
.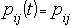 for all
for all 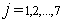 Our test hypothesis is stated as;
Our test hypothesis is stated as;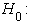 Transition probabilities are constant overtime
Transition probabilities are constant overtime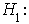 Transition probabilities are not constant overtimeTo test the stationarity of the seasonal TPM’s
Transition probabilities are not constant overtimeTo test the stationarity of the seasonal TPM’s 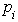 with elements
with elements 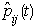 we use the following layout below.
we use the following layout below. 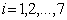 The
The 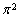 - test of stationarity specify that1. Transitions from row state
- test of stationarity specify that1. Transitions from row state 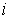 to state
to state 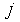 are stationary at
are stationary at 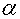 - level of significance if
- level of significance if 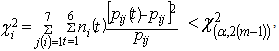
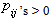 2. The entire TPM, P is constant overtime if
2. The entire TPM, P is constant overtime if 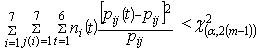
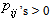 .
.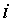 given entry in grade
given entry in grade 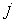 is given by
is given by 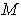 and the probability of attainment of grade
and the probability of attainment of grade 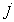 from grade
from grade 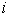 is given by
is given by 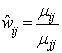
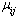 and
and 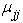 are element of the fundamental matrix
are element of the fundamental matrix 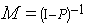

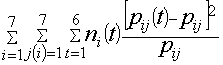 = 16.12Since, the p-value = 0.99 is greater than the
= 16.12Since, the p-value = 0.99 is greater than the 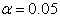 , we accept the null hypothesis of stationarity of the cadre transition.
, we accept the null hypothesis of stationarity of the cadre transition.



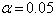 , we accept the null hypothesis of stationarity of the grade transition (see Table 3). We can denote from the result of the fundamental matrix (M) that an entrant on grade 1 (Assistant lecturer grade) is expected to stay for a period of 2 years and seven months in grade 1; an entrant on grade 2 (Lecturer III) is expected to stay for a period of 4 years and a month in grade 2; an entrant on grade 3 (Lecturer II) is expected to stay for a period of 3 years and 2 months in grade 3; an entrant on grade 4 (Lecturer I) is expected to stay for a period of 3 years and 4 months; an entrant on grade 5 (Senior Lecturer) is expected to stay for a period of 2 years and 11 months; an entrant on grade 6 (Principal Lecturer) is expected to stay for a period of 2 years and six months in grade 6; an entrant on grade 7 (Chief Lecturer) is expected to stay for a period of 4 years and 3 months in grade 7. Also, the career prospect analysis, the matrix
, we accept the null hypothesis of stationarity of the grade transition (see Table 3). We can denote from the result of the fundamental matrix (M) that an entrant on grade 1 (Assistant lecturer grade) is expected to stay for a period of 2 years and seven months in grade 1; an entrant on grade 2 (Lecturer III) is expected to stay for a period of 4 years and a month in grade 2; an entrant on grade 3 (Lecturer II) is expected to stay for a period of 3 years and 2 months in grade 3; an entrant on grade 4 (Lecturer I) is expected to stay for a period of 3 years and 4 months; an entrant on grade 5 (Senior Lecturer) is expected to stay for a period of 2 years and 11 months; an entrant on grade 6 (Principal Lecturer) is expected to stay for a period of 2 years and six months in grade 6; an entrant on grade 7 (Chief Lecturer) is expected to stay for a period of 4 years and 3 months in grade 7. Also, the career prospect analysis, the matrix 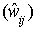 obtained showed that on the average potential entrants in grade 1 and 2 have 63% and 63% chances of being promoted to Lecturer II, entrant in grade3 have 55% chances of being promoted to Lecturer I, entrant in grade 4 have about 37% chance of being promoted to Senior Lecturer while entrants in grade 5 have about 75% chance of being promoted to Principal Lecturer and entrants in grade 6 have about 50% chance of being promoted to Chief Lecturer.From the graphical representation (see Figure 1) we observed that entrant into Principal Lecturer grade and Assistant Lecturer grade are expected to spend less years than the other grade levels with an expected length of 2 years and 6 months and 2 years and 7 months respectively.
obtained showed that on the average potential entrants in grade 1 and 2 have 63% and 63% chances of being promoted to Lecturer II, entrant in grade3 have 55% chances of being promoted to Lecturer I, entrant in grade 4 have about 37% chance of being promoted to Senior Lecturer while entrants in grade 5 have about 75% chance of being promoted to Principal Lecturer and entrants in grade 6 have about 50% chance of being promoted to Chief Lecturer.From the graphical representation (see Figure 1) we observed that entrant into Principal Lecturer grade and Assistant Lecturer grade are expected to spend less years than the other grade levels with an expected length of 2 years and 6 months and 2 years and 7 months respectively. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML

