| [1] | Asady, B. and Kajani, M.T., 2005, Direct method for solving integro-differential equations using hybrid Fourier and block pulse functions. Int. J. Comp. Math., 82(7), 889-895. |
| [2] | Avudainayagam, A. and Vani, C., 2000, Wavelet-Galerkin method for integro-differential equations. Appl. Numer. Math., 32, 247–254. |
| [3] | Barzkar, A., Oshagh, M.K., Assari, P. and Mehrpouya, M.A., 2012, Numerical solution of the nonlinear Fredholm integral equation and the Fredholm integro-differential equation of second kind using Chebyshev wavelets. World Appl. Sci. J., 18(12), 1774-1782. |
| [4] | Caglar, N. and Caglar, H., 2009, B-spline method for solving linear system of second-order boundary value problems. Comput. Math. Appl., 57: 757-762. |
| [5] | Christara, C. C., 1994, Quadratic spline collocation methods for elliptic partial differential equations. BIT, 34, 33-61. |
| [6] | Darania, P. and Ebadian, A., 2007, A method for the numerical solution of the integro differential equations. Appl. Math. and Comput., 188, 657-668. |
| [7] | El-Sayed, S.M. and Abdel-Aziz, M.R., 2003, A comparison of Adomian’s decomposition method and Wavelet-Galerkin method for solving integro-differential equations. Appl. Math. Comput. 136, 151–159. |
| [8] | Goh, J., Majid, A.A. and Ismail, A.I., 2011, Extended cubic uniform B-spline for a class of singular boundary value problems. ScienceAsaia, 37, 79-82. |
| [9] | Han, D.F. and Shang, X.F., 2007, Numerical solution of integro-differential equations by using CAS wavelet operational matrix of integration. Appl. Math. Comp. 194, 460 –466. |
| [10] | Houstis, E. N., Vavalis, E.A. and Rice, J.R., 1988, Convergence of an O(h4) cubic spline collocation method for elliptic partial differential equations. SIAM J. Numer. Anal., 25, 54-74. |
| [11] | Islam, S., Tirmizi, S.I.A. and Haq, F., 2007, Quartic non-polynomial spline approach to the solution of a system of second-order boundary value problems. Int. J. High Performance Computing Applications, 21, 42- 49. |
| [12] | Karamete, A. and Sezer, M., 2002, A Taylor collocation method for the solution of linear integro-differential equations. Int. J. Comp. Math., 79(9), 987–1000. |
| [13] | Netravali A.N. and Figueiredo, R.J.P., 1974, Spline approximation to the solution of the linear Fredholm integral equation of the second kind. SIAM. J. Numer. Anal, 11, 538-549. |
| [14] | Ogunlaran, O.M. and Taiwo, O.A., 2013, Spline methods for a class of singularly perturbed boundary value problems. Int. J. Math. Res., 2(1), 1-10. |
| [15] | Ogunlaran, O.M. and Akinlotan, O. F., 2013, A computational method for system of linear Fredholm integral equations. Mathematical Theory and Modeling, 3(4), 1-6. |
| [16] | Parand, K., Abbasbandy, S., Kazem S. and Rad, J. A., 2011, A novel application of radial basis functions for solving a model of first-order integro-ordinary differential equation. Comm. Nonlinear Sci. and Numer. Simul., 16(11), 4250–4258. |
| [17] | Prenter P.M., 1975, Spline and variational methods, Wiley-Iterscience, New York. |
| [18] | Rashidinia, J., Babolian, E. and Mahmoodi, Z., 2011, Spline collocation for Fredholm integral equations. Mathematical Sciences, 5(2), 147-158. |
| [19] | Schumaker, L. L., 2007, Spline functions: Basic theory, Cambridge University Press, New York. |
| [20] | Siddiqi, S.S. and Akram, G., 2006, Solution of fifth-order boundary value problems using non-polynomial spline technique. Appl. Math. Comput., 175: 1574-1581. |
| [21] | Taiwo, O.A. and Ogunlaran, O.M., 2008, Numerical solution of fourth order linear ordinary differential equations by cubic spline collocation tau method. J. Math. & Stat., 4(4), 264 - 268. |
| [22] | Taiwo, O.A. and Ogunlaran, O.M., 2011, A non-polynomial spline method for solving linear fourth order boundary value problems. Int. J. Phys. Sci., 6(13), 3246- 3254. |
| [23] | Taiwo, O.A., Adewumi, A.O. and Raji, R.A., 2012, Application of new homotopy analysis method for first and second orders integro- differential equations. Int.J. Sci. Tech., 2(5), 328-332. |
| [24] | Tavassoli, M.K., Ghasemi, M. and Babolian, E., 2006, Numerical solution of linear integro-differential equation by using Sine-Cosine wavelets. Appl. Math. Comput., 180, 569-574. |
| [25] | Tavassoli, M.K., Ghasemi. M. and Babolian, E., 2007, Comparison between Homotopy perturbation method and Sine-Cosine wavelets method for solving linear integro-differential equations. Int. J. Comput. Math. Appl., 54, 1162-1168. |
| [26] | Usmani, R.A., 1992, The use of quartic spline in the numerical solution of fourth order boundary value problem. J. Comput. Appl. Math., 44, 187-199. |

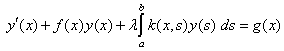
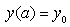
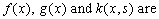
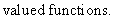
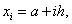
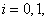
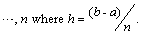 By following[21], the cubic spline
By following[21], the cubic spline 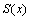 interpolating the functions
interpolating the functions 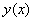 at the grid points is given by the equation
at the grid points is given by the equation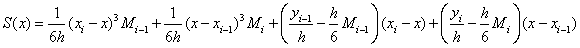
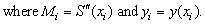 The unknown derivative
The unknown derivative 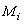 are related by enforcing the continuity condition on
are related by enforcing the continuity condition on 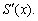 Differentiating (3), we obtain
Differentiating (3), we obtain 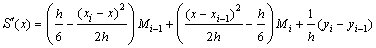
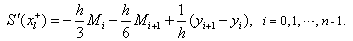
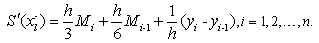
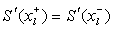 gives the consistency relation
gives the consistency relation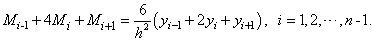
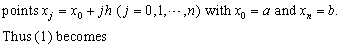
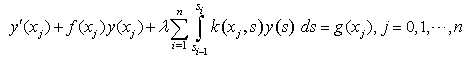
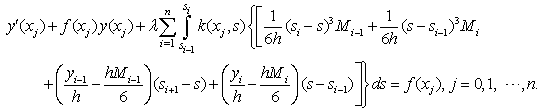
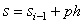 and simplifying, we obtain
and simplifying, we obtain 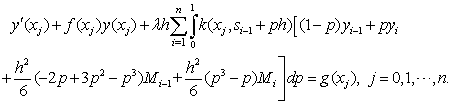
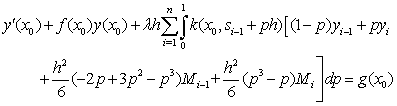
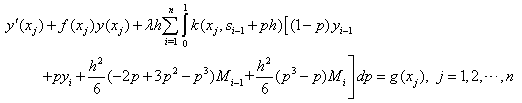
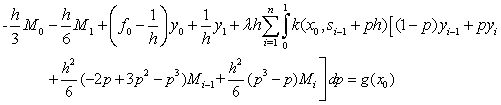
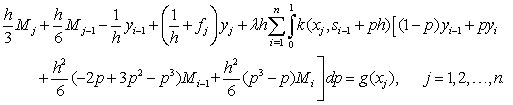
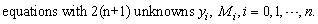 However, to determine the values of these unknowns, two more equations are required. These equations are obtained by using the initial condition (2) and by imposing a free boundary condition
However, to determine the values of these unknowns, two more equations are required. These equations are obtained by using the initial condition (2) and by imposing a free boundary condition 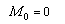
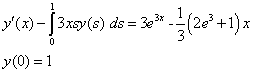
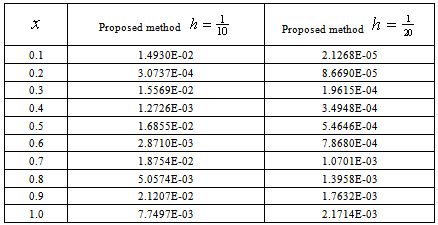
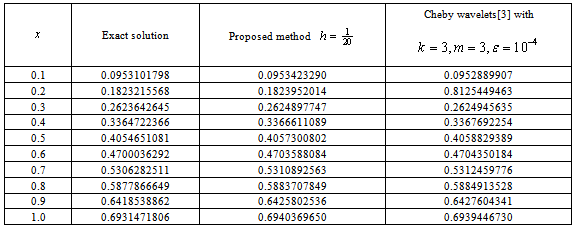
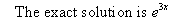 Example 3.2Consider the following integro-differential equation
Example 3.2Consider the following integro-differential equation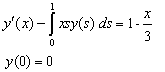
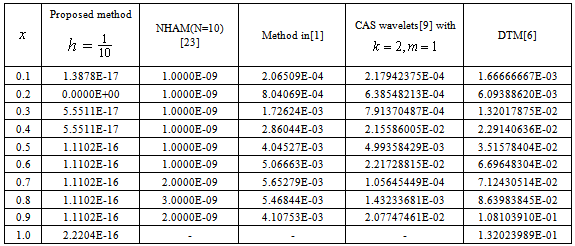
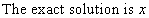 Example 3.3Consider
Example 3.3Consider 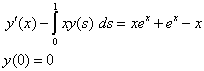
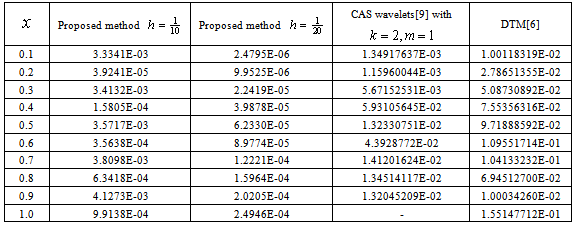
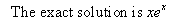 Example 3.4Consider
Example 3.4Consider 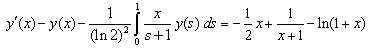
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML