| [1] | B. C. Bberndt, Ramanujan’s Notebooks Part II, Springer-Verlag, New York, 1989. |
| [2] | E. D. Rainville, Special Functions, Chelsea Publishing Company, Bronx, New York, 1960. |
| [3] | G. E. Andrws, R. Askey and R. Roy, Special Functions, Encyclopedia of Mathematics and its Applications Cambridge; Cambridge University Press, 1999, vol.71. |
| [4] | G. Gasper and M. Rahman, Basic Hypergeometric Series, vol. 96 of Encyclopedia of Mathematics and Its Applications, Cambridge University Press, Cambridge, UK, 2nd edition, 2004. |
| [5] | G. N. Watson, The cubic transformation of the hypergeometric function, Quart. Math. 41(1910), 70-79. |
| [6] | H. Exton, On the reducibility of the Kampe de Feriet function, Journal of Computational and Applied Mathematics vol.83, no.1 pp.119-121, 1997. |
| [7] | H. M. Srivastava, M. I. Qureshi, R. Singh, and A. Arora, A family of hypergeometric integrals associated with Ramanujan’s integral formula, Adv. Stud. Contemp. Math. 18 (2009), 113-125. |
| [8] | Kung-Yu Chen, Shuoh-Jung Liu, H. M. Srivastava, Some double-series identities and associated generating-function relationships, Applied Mathematics Letters, 19 (2006) 887-893. |
| [9] | L. J. Slater, Generalized Hypergeometric Functions, Cambridge University Press, Cam- bridge, London and New York, 1966. |
| [10] | M. A. Rakha, Adel K. Ibrahim, and Arjun K. Rathie, On the computations of contiguous relations for 2F1 hypergeometric series, Commun. Korean Math. Soc. 24 (2009), No.2, pp.291-302. |
| [11] | Pankaj Srivastava, Certain transformations of generalized Kampe de Feriet function Vijnana Parishad Anusandan Patrika. Vol.45, No.4, (2002), pp.383-392. |
| [12] | R. K. Saxena, C. Ram and N. Dudi, Some results associated with a generalized hyper- geometric function, Bulletin of Pure and Applied Sciences. Vol.24 (No.2) 2005, 305-316. |
| [13] | R. P. Agarwal, Special function and their application, Keynote address, Proceedings of National Symposium on special Function and their application (Gorakhpur 1986). |
| [14] | R. P. Singh, A note on double transformation of certain hypergeometric functions, Proceedings Edinburgh Math. Soc. (2), 14(1956), 221-227. |
| [15] | R. Y. Denis and S. N. Singh, Hypergeometric Functions and Continued Fractions, Far East J. Math. Sci. 2(3) (2000), 385-400. |
| [16] | S. N. Singh and S. P. Singh, Transformation of Kampe De Feriet function, Indian J. of Pure and Appl. Math. 13(10), October 1982. |
| [17] | S. P. Singh, Certain theorems involving ordinary hypergeometric functions of one and two variables, South East Asian J. Math. And Mathematical. Soc. Vol.3 no.3 (2005), pp.59-63. |
| [18] | W. N. Bailey, Generalized hypergeometric series, Cambridge University Press, Cambridge (1935), reprinted by Stechert-Hafner, New York (1964). |
| [19] | Yong S. Kim, Tibor K. Pogany and Arjun K. Rathi, On a summation formula for the clausen’s series 3F2 with applications Miskolc Mathematical Notes, Vol.10 (2009), No.2, pp.145-153. |

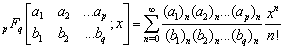 Where
Where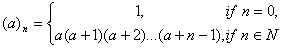 The series converges when none of denominator parameter are zero or negative integer. It is converges for all x when p<q, for |x|<1, it is converges when p=q+1and for |x|<1 it is converges when Re(∑bi-∑ai)>0 and it is only converges for x=0 when x=0 when p>q+1 unless it reduces to a polynomial.A Kampe de Feriet hypergeometric function of two variables is defined as,
The series converges when none of denominator parameter are zero or negative integer. It is converges for all x when p<q, for |x|<1, it is converges when p=q+1and for |x|<1 it is converges when Re(∑bi-∑ai)>0 and it is only converges for x=0 when x=0 when p>q+1 unless it reduces to a polynomial.A Kampe de Feriet hypergeometric function of two variables is defined as, 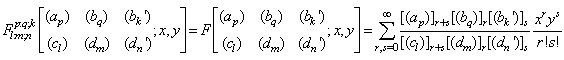 Where (ap) stands for the sequence of p parameters a1,…ap and |x|<1, |y|<1, l+m+n<p+q+k+1 for convergence.We shall use the following known transformations and identity in our analysis as given in[1, 2, 4, 9]
Where (ap) stands for the sequence of p parameters a1,…ap and |x|<1, |y|<1, l+m+n<p+q+k+1 for convergence.We shall use the following known transformations and identity in our analysis as given in[1, 2, 4, 9]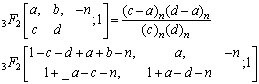
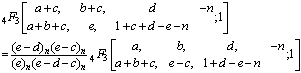
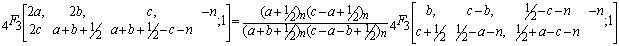
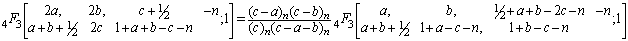
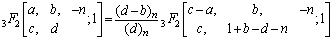
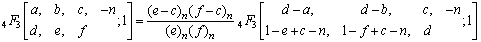
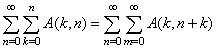
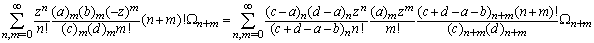
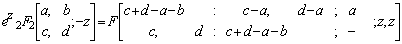
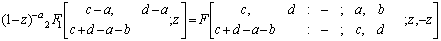
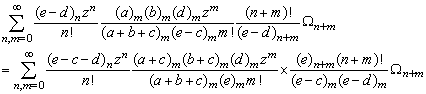
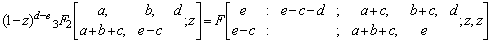
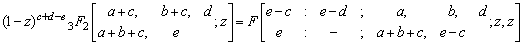
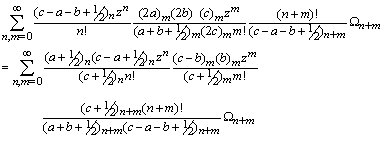
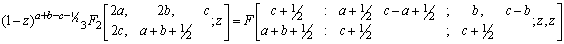
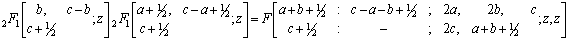
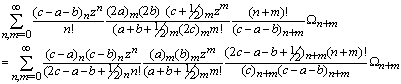
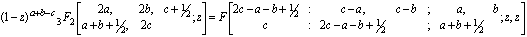
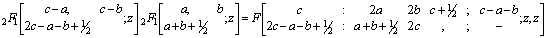
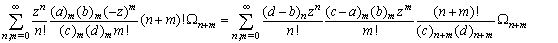
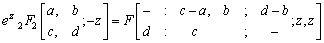
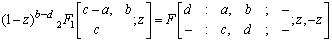
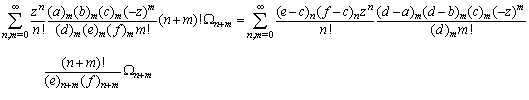
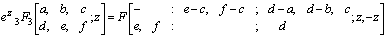
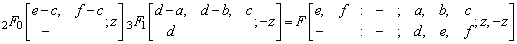
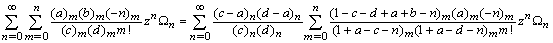 Making use of the identity (7) and (a-n)n=(-1)n(1-a)n in above we get after some simplification,
Making use of the identity (7) and (a-n)n=(-1)n(1-a)n in above we get after some simplification,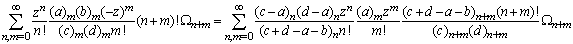
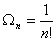 and after some simplification we get,
and after some simplification we get, 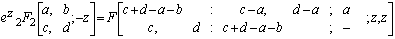
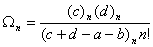 in eq. (14a) and after some simplification we get,
in eq. (14a) and after some simplification we get, 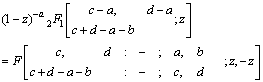
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML