R. Thukral
Padé Research Centre, 39 Deanswood Hill, Leeds, West Yorkshire, LS17 5JS, England
Correspondence to: R. Thukral, Padé Research Centre, 39 Deanswood Hill, Leeds, West Yorkshire, LS17 5JS, England.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
In this paper, we present a new family of multipoint iterative methods for finding multiple zeros of nonlinear equations. Per iteration the new method requires three evaluations of functions and one of its first derivative. We have analysed and proved the order of convergence of the new methods. Finally, the numerical examples demonstrate that the proposed methods are superior to the existing methods.
Keywords:
Modified Newton Method, Root-Finding, Nonlinear Equations, Multiple Roots, Order of Convergence, Efficiency Index
Cite this paper: R. Thukral, A New Family of Multipoint Iterative Methods for Finding Multiple Roots of Nonlinear Equations, American Journal of Computational and Applied Mathematics , Vol. 3 No. 3, 2013, pp. 168-173. doi: 10.5923/j.ajcam.20130303.03.
1. Introduction
Finding the roots of nonlinear equations is very important in numerical analysis and has many applications in engineering and other applied sciences. In this paper, we consider iterative methods to find a multiple root 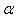 of multiplicity m, i.e.,
of multiplicity m, i.e., 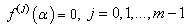 and
and 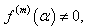 of a nonlinear equation
of a nonlinear equation 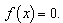 | (1) |
where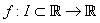 is a scalar function on an open interval I and it is sufficiently smooth in the neighbourhood of
is a scalar function on an open interval I and it is sufficiently smooth in the neighbourhood of 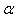 . In recent years, some modifications of the Newton method for multiple roots have been proposed and analysed [2-12]. However, there are not many methods known to handle the case of multiple roots. Hence we present two new iterative methods of higher order for finding multiple zeros of a nonlinear equation and only use four evaluations of the function per iteration. In addition, the new methods have a better efficiency index than the third and fourth order methods given in [2,3-12]. In view of this fact, the new methods are significantly better when compared with the established methods. Consequently, we have found that the new methods are efficient and robust. The well-known Newton’s method for finding multiple roots is given by
. In recent years, some modifications of the Newton method for multiple roots have been proposed and analysed [2-12]. However, there are not many methods known to handle the case of multiple roots. Hence we present two new iterative methods of higher order for finding multiple zeros of a nonlinear equation and only use four evaluations of the function per iteration. In addition, the new methods have a better efficiency index than the third and fourth order methods given in [2,3-12]. In view of this fact, the new methods are significantly better when compared with the established methods. Consequently, we have found that the new methods are efficient and robust. The well-known Newton’s method for finding multiple roots is given by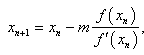 | (2) |
which converges quadratically [1,10]. For the purpose of this paper, we use (2) to construct new multipoint iterative methods for finding multiple roots of a nonlinear equation.
2. Construction of the Methods and Convergence Analysis
In this section we define two new iterative methods. In order to establish the order of convergence of the new methods we state the three essential definitions.Definition 1 Let 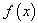 be a real function with a simple root
be a real function with a simple root 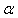 and let
and let 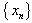 be a sequence of real numbers that converge towards
be a sequence of real numbers that converge towards 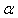 . The order of convergence p is given by
. The order of convergence p is given by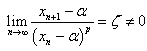 | (3) |
where 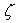 is the asymptotic error constant and
is the asymptotic error constant and 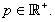 Definition 2 Let k be the number of function evaluations of the new method. The efficiency of the new method is measured by the concept of efficiency index [1,10] and defined as
Definition 2 Let k be the number of function evaluations of the new method. The efficiency of the new method is measured by the concept of efficiency index [1,10] and defined as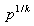 | (4) |
where p is the order of the method.Definition 3 Suppose that 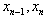 and
and 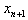 are three successive iterations closer to the root
are three successive iterations closer to the root 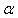 of (1). Then the computational order of convergence [11] may be approximated by
of (1). Then the computational order of convergence [11] may be approximated by 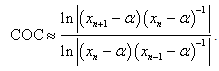 | (5) |
where 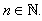 Recently Thukral [7] presented a fourth-order method for finding multiple roots of a nonlinear equation, which is given as
Recently Thukral [7] presented a fourth-order method for finding multiple roots of a nonlinear equation, which is given as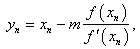 | (6) |
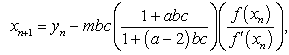 | (7) |
where 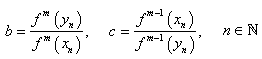 ,
, 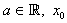 is the initial value and provided that the denominator of (6) and (7) are not equal to zero.In fact, the new iterative methods presented in this paper are the extension of the above scheme. To develop the higher order iterative methods we use the above two steps and introduce the third step with a new parameter. First we define sixth-order iterative method and then followed by fifth-order iterative method.
is the initial value and provided that the denominator of (6) and (7) are not equal to zero.In fact, the new iterative methods presented in this paper are the extension of the above scheme. To develop the higher order iterative methods we use the above two steps and introduce the third step with a new parameter. First we define sixth-order iterative method and then followed by fifth-order iterative method.
2.1. The New Sixth-order Iterative Method
The new sixth-order method for finding multiple root of a nonlinear equation is expressed as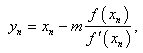 | (8) |
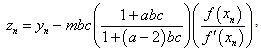 | (9) |
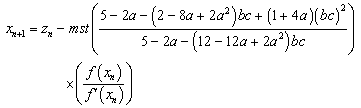 | (10) |
where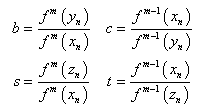 | (11) |
and 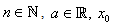 is the initial value.Theorem 1 Let
is the initial value.Theorem 1 Let 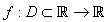 be a sufficiently smooth function defined on an open interval D, enclosing a multiple zero of
be a sufficiently smooth function defined on an open interval D, enclosing a multiple zero of 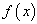 , with multiplicity
, with multiplicity 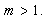 Then the family of iterative methods defined by scheme (10) has sixth-order convergence. Proof Let
Then the family of iterative methods defined by scheme (10) has sixth-order convergence. Proof Let 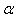 be a multiple root of multiplicity m of a sufficiently smooth function
be a multiple root of multiplicity m of a sufficiently smooth function 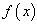 ,
, 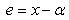 and
and 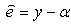 , where y is defined in (8).Using Taylor expansion of
, where y is defined in (8).Using Taylor expansion of 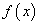 and
and 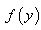 about
about 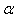 , we have
, we have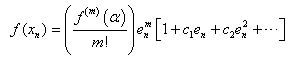 | (12) |
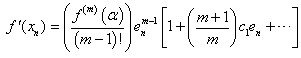 | (13) |
where 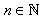 and
and 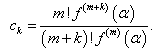 | (14) |
Moreover by (8), we have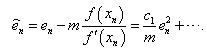 | (15) |
The expansion of 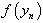 about
about 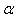 is given as
is given as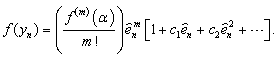 | (16) |
Simplifying (16), we get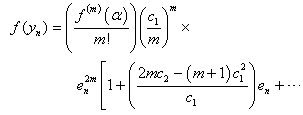 | (17) |
Furthermore, we have 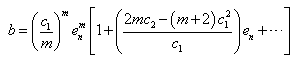 | (18) |
Since from (9) and (10), we have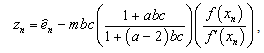 | (19) |
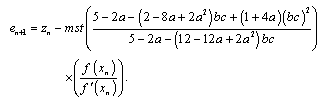 | (20) |
Substituting appropriate expressions in (10) and after simplification we obtain the error equation.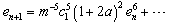 | (21) |
The error equation (21) establishes the fourth-order convergence of the new method defined by (10).
2.2. The New Fifth-Order Iterative Method
The new fifth-order method for finding multiple root of a nonlinear equation is expressed as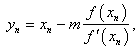 | (22) |
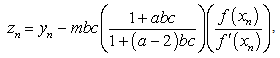 | (23) |
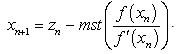 | (24) |
where 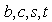 are given in (11),
are given in (11), 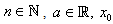 is the initial value and provided that the denominator of (22)-(24) are not equal to zero.Theorem 2Let
is the initial value and provided that the denominator of (22)-(24) are not equal to zero.Theorem 2Let 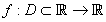 be a sufficiently smooth function defined on an open interval D, enclosing a multiple zero of
be a sufficiently smooth function defined on an open interval D, enclosing a multiple zero of 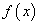 , with multiplicity
, with multiplicity 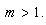 Then the family of iterative methods defined by scheme (24) has fifth-order convergence. ProofSubstituting appropriate expressions in (24) and after simplification we obtain the error equation
Then the family of iterative methods defined by scheme (24) has fifth-order convergence. ProofSubstituting appropriate expressions in (24) and after simplification we obtain the error equation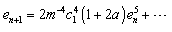 | (25) |
The error equation (25) establishes the fifth-order convergence of the new method defined by (24).
3. The Established Methods
For the purpose of comparison, we consider one sixth-order methods and two fifth-order methods presented recently in [8,9]. Since these methods are well established, we shall state the essential expressions used in order to calculate the approximate solution of the given nonlinear equations and thus compare the effectiveness of the new multipoint order methods for finding multiple roots. In [9], Thukral developed a sixth and fifth order of convergence methods, since these methods are well established we state the essential expressions used in each of the methods. The sixth-order method for finding multiple roots of a nonlinear equation is expressed as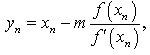 | (26) |
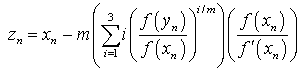 | (27) |
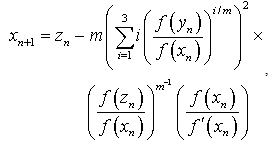 | (28) |
where 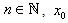 is the initial value and provided that the denominators of (6) and (7) are not equal to zero.The second of the method given in[9] is the fifth-order method for finding multiple root of a nonlinear equation is expressed as
is the initial value and provided that the denominators of (6) and (7) are not equal to zero.The second of the method given in[9] is the fifth-order method for finding multiple root of a nonlinear equation is expressed as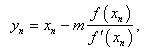 | (29) |
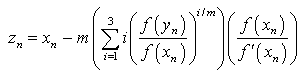 | (30) |
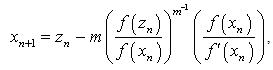 | (31) |
where 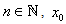 is the initial value and provided that the denominators of (20)- (22) are not equal to zero.In [8] Thukral developed another fifth-order method for finding multiple root of a nonlinear equation is expressed as
is the initial value and provided that the denominators of (20)- (22) are not equal to zero.In [8] Thukral developed another fifth-order method for finding multiple root of a nonlinear equation is expressed as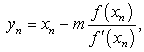 | (32) |
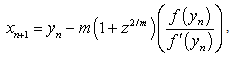 | (33) |
where  is the initial value and provided that the denominators of (6) and (7) are not equal to zero.
is the initial value and provided that the denominators of (6) and (7) are not equal to zero.
4. Application of the New Multipoint Iterative Methods
The present multipoint methods given by (10) and (24) are employed to solve nonlinear equations with multiple roots and compare with the Thukral methods, (28), (31) and (33). To demonstrate the performance of the new multipoint methods, we use ten particular nonlinear equations. We determine the consistency and stability of results by examining the convergence of the new iterative methods. The findings are generalised by illustrating the effectiveness of the new multipoint methods for determining the multiple root of a nonlinear equation. Consequently, we give estimates of the approximate solution produced by the methods considered and list the errors obtained by each of the methods. The numerical computations listed in the tables were performed on an algebraic system called Maple. In fact, the errors displayed are of absolute value and insignificant approximations by the various methods have been omitted in the following tables.The new multipoint method requires four function evaluations. To determine the efficiency index of the new methods, we shall use the definition 2. Hence, the efficiency index of the multipoint method given by (10) is 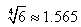 whereas the efficiency index of the fifth-order method is given as
whereas the efficiency index of the fifth-order method is given as 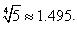 We can see that the efficiency index of the new sixth-order method is better than the other similar methods. The test functions and their exact root
We can see that the efficiency index of the new sixth-order method is better than the other similar methods. The test functions and their exact root 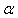 are displayed in table 1. The difference between the root
are displayed in table 1. The difference between the root 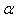 and the approximation
and the approximation 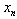 for test functions with initial estimate
for test functions with initial estimate 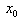 , are displayed in Table 2. In fact,
, are displayed in Table 2. In fact, 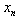 is calculated by using the same total number of function evaluations (TNFE) for all methods. In the calculations, 12 TNFE are used by each method. Furthermore, the computational order of convergence (COC) is displayed in Table 3.
is calculated by using the same total number of function evaluations (TNFE) for all methods. In the calculations, 12 TNFE are used by each method. Furthermore, the computational order of convergence (COC) is displayed in Table 3.Table 1. Test functions and their roots
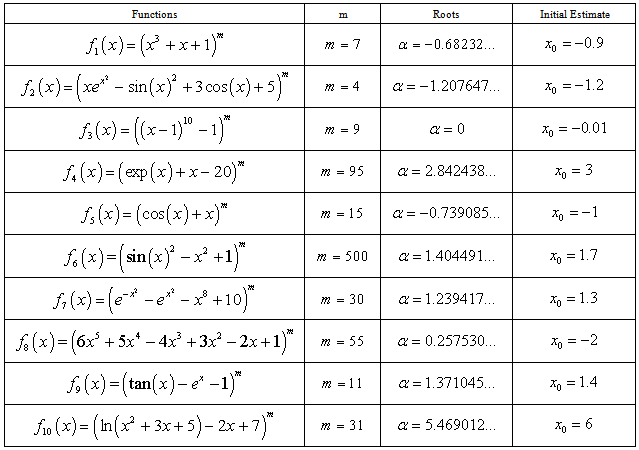 |
| |
|
Table 2. Comparison of various iterative methods
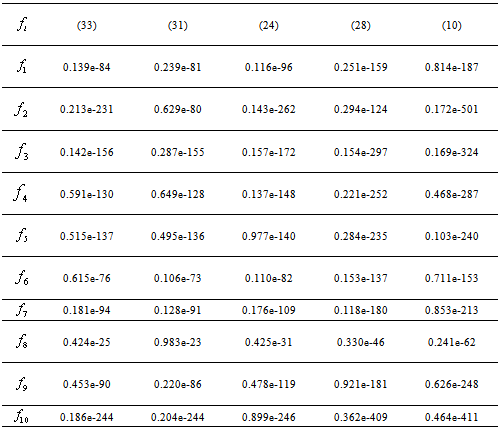 |
| |
|
Table 3. COC of various iterative methods
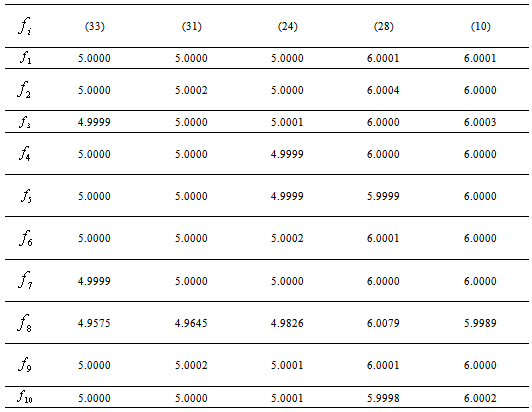 |
| |
|
5. Remarks and Conclusions
In this paper, we have introduced two new multipoint iterative methods for solving nonlinear equations with multiple roots. Convergence analysis proves that the new methods preserve their order of convergence. Simply introducing new parameter in (10) we have achieved sixth-order of convergence. The prime motive of presenting these new methods was to establish a higher order of convergence method than the existing third, fourth and fifth order methods [2-12]. We have examined the effectiveness of the new iterative methods by showing the accuracy of the multiple roots of several nonlinear equations. After an extensive experimentation, it can be concluded that the convergence of the tested multipoint methods of the sixth order is remarkably fast. Furthermore, in most of the test examples, empirically we have found that the best results of the new iterative methods (10) are obtained when 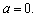 The main purpose of demonstrating the new methods for different types of nonlinear equations was purely to illustrate the accuracy of the approximate solution, the stability of the convergence, the consistency of the results and to determine the efficiency of the new iterative method. The major advantages of the new multipoint iterative methods are; first, able to evaluate simple and multiple roots, secondly, simple formula when compared to existing methods containing long expressions of m (see[3]), thirdly, produces better estimate than the similar methods. Finally, we conjecture that new concept introduced in this paper by Thukral may be applied to transform the iterative methods used for finding simple root of nonlinear equations.
The main purpose of demonstrating the new methods for different types of nonlinear equations was purely to illustrate the accuracy of the approximate solution, the stability of the convergence, the consistency of the results and to determine the efficiency of the new iterative method. The major advantages of the new multipoint iterative methods are; first, able to evaluate simple and multiple roots, secondly, simple formula when compared to existing methods containing long expressions of m (see[3]), thirdly, produces better estimate than the similar methods. Finally, we conjecture that new concept introduced in this paper by Thukral may be applied to transform the iterative methods used for finding simple root of nonlinear equations.
References
| [1] | W. Gautschi, Numerical Analysis: an Introduction, Birkhauser, 1997. |
| [2] | S. Kumar, V. Kanwar, S. Singh, On some modified families of multipoint iterative methods for multiple roots of solving nonlinear equations, Appl. Math. Comput. 218 (2012) 7382-7394. |
| [3] | S. G. Li, L. Z. Cheng, B. Neta, Some fourth-order nonlinear solvers with closed formulae for multiple roots, Comp. Math. Appl. 58 (2010) 126-135. |
| [4] | J. Peng, Z. Zeng, An approach finding multiple roots of nonlinear equations or polynomials, Adv. Elec. Comm. Web Appl. Comm. 149 (2012) 83-87. |
| [5] | E. Schroder, Uber unendich viele Algorithmen zur Auflosung der Gleichungen, Math. Ann. 2 (1870) 317-365. |
| [6] | R. Thukral, A new third-order iterative method for solving nonlinear equations with multiple roots, J. Math. Comput. 6 (2010) 61-68. |
| [7] | R. Thukral, A new family of fourth-order iterative methods for solving nonlinear equations with multiple roots, submitted to J. Numer. Math. Stoch. 2012. |
| [8] | R. Thukral, A new fifth-order iterative method for finding multiple roots of nonlinear equations, Amer. J. Comput. Math. 6 (2012) 260-264. |
| [9] | R. Thukral, Introduction to higher order iterative methods for finding multiple roots of solving nonlinear equations, J. Math. Vol. 2013, doi: 10.1155/2013/404635 . |
| [10] | J. F. Traub, Iterative Methods for solution of equations, Chelsea publishing company, New York 1977. |
| [11] | S. Weerakoon, T. G. I. Fernando, A variant of Newton’s method with accelerated third-order convergence, Appl. Math. Lett. 13 (2000) 87-93. |
| [12] | Z. Wu, X. Li, A fourth-order modification of Newton’s method for multiple roots, IJRRAS 10 (2) (2012) 166-170. |

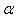 of multiplicity m, i.e.,
of multiplicity m, i.e., 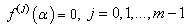 and
and 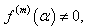 of a nonlinear equation
of a nonlinear equation 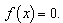
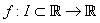 is a scalar function on an open interval I and it is sufficiently smooth in the neighbourhood of
is a scalar function on an open interval I and it is sufficiently smooth in the neighbourhood of 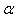 . In recent years, some modifications of the Newton method for multiple roots have been proposed and analysed [2-12]. However, there are not many methods known to handle the case of multiple roots. Hence we present two new iterative methods of higher order for finding multiple zeros of a nonlinear equation and only use four evaluations of the function per iteration. In addition, the new methods have a better efficiency index than the third and fourth order methods given in [2,3-12]. In view of this fact, the new methods are significantly better when compared with the established methods. Consequently, we have found that the new methods are efficient and robust. The well-known Newton’s method for finding multiple roots is given by
. In recent years, some modifications of the Newton method for multiple roots have been proposed and analysed [2-12]. However, there are not many methods known to handle the case of multiple roots. Hence we present two new iterative methods of higher order for finding multiple zeros of a nonlinear equation and only use four evaluations of the function per iteration. In addition, the new methods have a better efficiency index than the third and fourth order methods given in [2,3-12]. In view of this fact, the new methods are significantly better when compared with the established methods. Consequently, we have found that the new methods are efficient and robust. The well-known Newton’s method for finding multiple roots is given by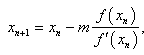
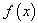 be a real function with a simple root
be a real function with a simple root 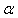 and let
and let 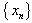 be a sequence of real numbers that converge towards
be a sequence of real numbers that converge towards 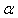 . The order of convergence p is given by
. The order of convergence p is given by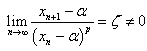
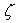 is the asymptotic error constant and
is the asymptotic error constant and 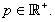 Definition 2 Let k be the number of function evaluations of the new method. The efficiency of the new method is measured by the concept of efficiency index [1,10] and defined as
Definition 2 Let k be the number of function evaluations of the new method. The efficiency of the new method is measured by the concept of efficiency index [1,10] and defined as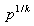
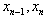 and
and 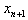 are three successive iterations closer to the root
are three successive iterations closer to the root 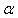 of (1). Then the computational order of convergence [11] may be approximated by
of (1). Then the computational order of convergence [11] may be approximated by 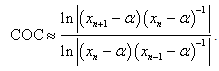
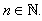 Recently Thukral [7] presented a fourth-order method for finding multiple roots of a nonlinear equation, which is given as
Recently Thukral [7] presented a fourth-order method for finding multiple roots of a nonlinear equation, which is given as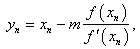
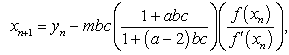
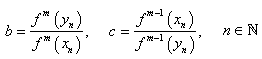 ,
, 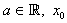 is the initial value and provided that the denominator of (6) and (7) are not equal to zero.In fact, the new iterative methods presented in this paper are the extension of the above scheme. To develop the higher order iterative methods we use the above two steps and introduce the third step with a new parameter. First we define sixth-order iterative method and then followed by fifth-order iterative method.
is the initial value and provided that the denominator of (6) and (7) are not equal to zero.In fact, the new iterative methods presented in this paper are the extension of the above scheme. To develop the higher order iterative methods we use the above two steps and introduce the third step with a new parameter. First we define sixth-order iterative method and then followed by fifth-order iterative method.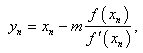
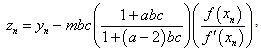
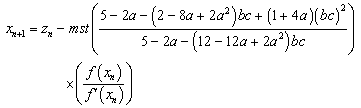
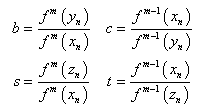
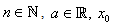 is the initial value.Theorem 1 Let
is the initial value.Theorem 1 Let 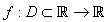 be a sufficiently smooth function defined on an open interval D, enclosing a multiple zero of
be a sufficiently smooth function defined on an open interval D, enclosing a multiple zero of 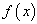 , with multiplicity
, with multiplicity 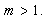 Then the family of iterative methods defined by scheme (10) has sixth-order convergence. Proof Let
Then the family of iterative methods defined by scheme (10) has sixth-order convergence. Proof Let 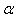 be a multiple root of multiplicity m of a sufficiently smooth function
be a multiple root of multiplicity m of a sufficiently smooth function 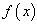 ,
, 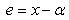 and
and 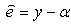 , where y is defined in (8).Using Taylor expansion of
, where y is defined in (8).Using Taylor expansion of 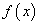 and
and 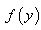 about
about 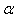 , we have
, we have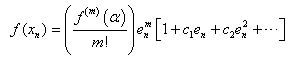
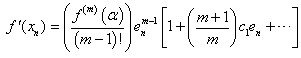
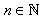 and
and 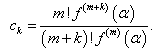
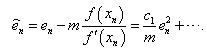
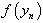 about
about 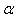 is given as
is given as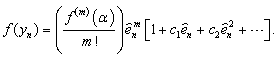
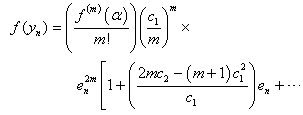
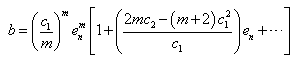
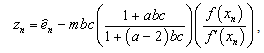
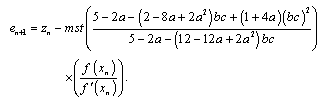
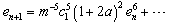
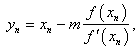
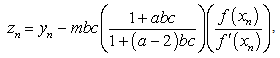
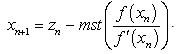
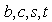 are given in (11),
are given in (11), 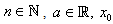 is the initial value and provided that the denominator of (22)-(24) are not equal to zero.Theorem 2Let
is the initial value and provided that the denominator of (22)-(24) are not equal to zero.Theorem 2Let 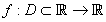 be a sufficiently smooth function defined on an open interval D, enclosing a multiple zero of
be a sufficiently smooth function defined on an open interval D, enclosing a multiple zero of 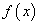 , with multiplicity
, with multiplicity 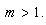 Then the family of iterative methods defined by scheme (24) has fifth-order convergence. ProofSubstituting appropriate expressions in (24) and after simplification we obtain the error equation
Then the family of iterative methods defined by scheme (24) has fifth-order convergence. ProofSubstituting appropriate expressions in (24) and after simplification we obtain the error equation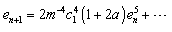
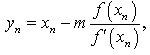
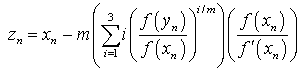
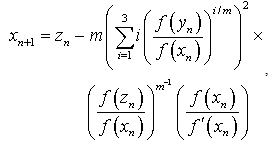
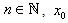 is the initial value and provided that the denominators of (6) and (7) are not equal to zero.The second of the method given in[9] is the fifth-order method for finding multiple root of a nonlinear equation is expressed as
is the initial value and provided that the denominators of (6) and (7) are not equal to zero.The second of the method given in[9] is the fifth-order method for finding multiple root of a nonlinear equation is expressed as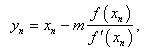
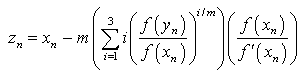
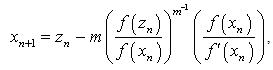
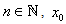 is the initial value and provided that the denominators of (20)- (22) are not equal to zero.In [8] Thukral developed another fifth-order method for finding multiple root of a nonlinear equation is expressed as
is the initial value and provided that the denominators of (20)- (22) are not equal to zero.In [8] Thukral developed another fifth-order method for finding multiple root of a nonlinear equation is expressed as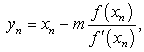
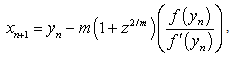
 is the initial value and provided that the denominators of (6) and (7) are not equal to zero.
is the initial value and provided that the denominators of (6) and (7) are not equal to zero.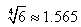 whereas the efficiency index of the fifth-order method is given as
whereas the efficiency index of the fifth-order method is given as 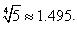 We can see that the efficiency index of the new sixth-order method is better than the other similar methods. The test functions and their exact root
We can see that the efficiency index of the new sixth-order method is better than the other similar methods. The test functions and their exact root  are displayed in table 1. The difference between the root
are displayed in table 1. The difference between the root 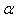 and the approximation
and the approximation 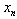 for test functions with initial estimate
for test functions with initial estimate 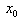 , are displayed in Table 2. In fact,
, are displayed in Table 2. In fact, 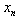 is calculated by using the same total number of function evaluations (TNFE) for all methods. In the calculations, 12 TNFE are used by each method. Furthermore, the computational order of convergence (COC) is displayed in Table 3.
is calculated by using the same total number of function evaluations (TNFE) for all methods. In the calculations, 12 TNFE are used by each method. Furthermore, the computational order of convergence (COC) is displayed in Table 3.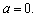 The main purpose of demonstrating the new methods for different types of nonlinear equations was purely to illustrate the accuracy of the approximate solution, the stability of the convergence, the consistency of the results and to determine the efficiency of the new iterative method. The major advantages of the new multipoint iterative methods are; first, able to evaluate simple and multiple roots, secondly, simple formula when compared to existing methods containing long expressions of m (see[3]), thirdly, produces better estimate than the similar methods. Finally, we conjecture that new concept introduced in this paper by Thukral may be applied to transform the iterative methods used for finding simple root of nonlinear equations.
The main purpose of demonstrating the new methods for different types of nonlinear equations was purely to illustrate the accuracy of the approximate solution, the stability of the convergence, the consistency of the results and to determine the efficiency of the new iterative method. The major advantages of the new multipoint iterative methods are; first, able to evaluate simple and multiple roots, secondly, simple formula when compared to existing methods containing long expressions of m (see[3]), thirdly, produces better estimate than the similar methods. Finally, we conjecture that new concept introduced in this paper by Thukral may be applied to transform the iterative methods used for finding simple root of nonlinear equations. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML

