1. Introduction

Let G = (V,E) be a simple graph. A subset D of V is a dominating set of G if every vertex of V- D is adjacent to a vertex of D. The domination number of G, denoted by γ(G), is the minimum cardinality of a dominating set of G.[1,2]

A (1,2) - dominating set in a graph G = (V,E) is a set S having the property that for every vertex v in V - S there is atleast one vertex in S at distance 1 from v and a second vertex in S at distance almost 2 from v. The order of the smallest (1,2) - dominating set of G is called the (1,2) - domination number of G and we denote it by γ_(1,2).[7]

The line graph L(G) of a graph G = (V,E) is a graph with vertex set E(G) in which two vertices are adjacent if and only if the corresponding edges in G are adjacent.[8]

2. (1,2) - domination in Paths

Throughout this paper P_n denotes a path on n vertices, C_n denotes a cycle with n vertices and K_1,n is a star graph.

Consider the following paths

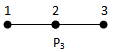{2,3} is a (1,2) - dominating set.

γ_(1,2) = 2

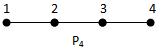{2,3} is a (1,2) - dominating set.

γ_(1,2) = 2

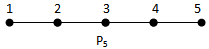{2,3,4 } is a (1,2) - dominating set.

γ_(1,2) = 3

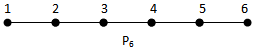{2,3,4,5} is a (1,2) - dominating set.

γ_(1,2) = 4

{2,3,4,5,6} is a (1,2) - dominating set.

γ_(1,2) = 5

{2,3,4,5,6,7} is a (1,2) - dominating set.

γ_(1,2) = 6

{2,3,4,5,6,7,8} is a (1,2) - dominating set.

γ_(1,2) = 7

{2,3,4,5,6,7,8,9} is a (1,2) - dominating set.

γ_(1,2) = 8

From the above examples we have the following theorem.

Theorem 2.1

(1,2) - domination number of a path graph P_n, for n ≥ 4 is n-2.

Proof:

Let P_n be a path with n vertices v₁, v₂, ...,v_n. Then v₂, v₃, ...,v_n-1 are of degree 2 ,v₁ and v₂ are of degree 1. That is n-2 vertices are of degree 2. Each vertex v₁ is adjacent to v_i+1. Therefore, v_i's are at distance one from v_i+1. Each vertex v_i+2 is at distance 2 from v_i. So to form a (1,2) - dominating set we have to include all those vertices of degree 2. But there are n-2 vertices of degree 2.

Hence γ_(1,2) = n-2.

The following lemma is due to Gray Chartrand and Ping Zhang.[3]

Lemma 1. γ( P_n) =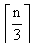

The following theorem gives the relationship between domination number and (1,2)-domination number.

Theorem 2.2

The domination number of the path P_n is less than (1,2) domination number.

Proof:

We have γ(P_n) =

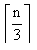In a graph G, domination number is less than or equals (1,2) domination number[6]. Let G be a graph and D be its dominating set. Then every vertex in V-D is adjacent to a vertex in D. That is, in D, for every vertex u, there is a vertex which is at distance 1 from u. But it is not necessary that there is a second vertex at distance atmost 2 from u. So if we find a (1,2)- dominating set, it will contain more vertices or atleast equal number of vertices than the dominating set. So the domination number is less than or equal to (1,2)-domination number.In particular, for paths domination number is less than(1,2) domination number. Hence the theorem.

3. (1,2)-domination in Cycles

Consider the following cycles

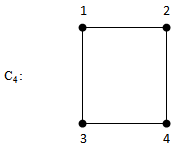{2,3} is a (1,2) - dominating set.

γ_(1,2) = 2

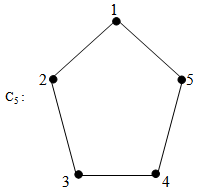{1,3,4} is a (1,2) - dominating set.

γ_(1,2) = 3

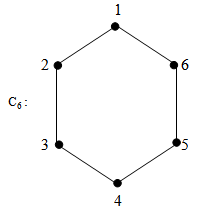{1,2,4} is a (1,2) - dominating set. γ_(1,2) = 3

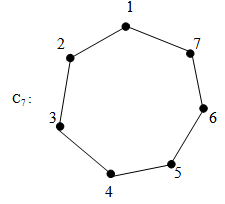{1,3,4,7} is a (1,2) - dominating set.

γ_(1,2) = 4

From the above examples we have the following theorem.

Theorem 3.1

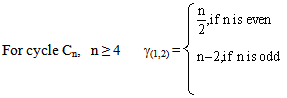Proof:

Every cycle C_n have n vertices and n edges in which each vertex is of degree 2. That is each vertex dominates two vertices .

Case 1: n is even.

Let v₁, v₂, ...,v_n be the vertices of C_n. v₁ and v_n are adjacent. Also v₁ is adjacent to v₂, v₂ is adjacent to v₃ and so on. Each v_i, 1 < i < n is not adjacent to v_i+2, v_i+3, v_i+4,..., v_n-1. Let us construct a (1,2) - dominating set. If we take the vertex v₁,v₁ is adjacent to v₂ and v_n and non-adjacent to all other n-2 vertices. v₃ and v_n-1 are at distance 2 from v₁. So we have to take v₂ and any one of v₃, v_n-1 in the set. If we take v₂, v₂ is adjacent to v₁ and v₃ and non- adjacent to v₄, v₅, ... v_n. That is n-3 vertices and v₄ and v_n-2 are at distance 2 from v₂. Similarly we can proceed upto all the n vertices. Finally we get a (1,2)- dominating set containing v₁, v₂, v₄, v₆,.., v_n-2. The cardinality of this set is 1+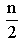-1, that is . Hence γ_(1,2) = 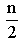, if n is even

Case 2: n is odd

If n is odd, we remove one vertex v₁, then the other n-1 vertices form a path P_n-1 and n-1 is even. But (1,2) - domination number of P_n-1 is n- 3. These n-3 vertices and the vertex v₁ from a (1,2) dominating set. Hence the cardinality of the (1,2) dominating set is n- 3+1. that is n-2. Hence γ_(1,2) = n-2, if n is odd.

4. (1,2)-domination in Star Graphs

Consider the following star graphs.

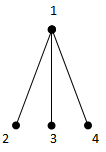{1,2} form a (1,2) - dominating set.

γ_(1,2) = 2

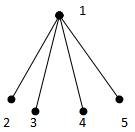{1,2} form a (1,2) - dominating set.

γ_(1,2) = 2

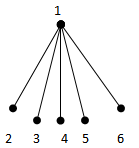{1,2} form a (1,2) - dominating set. γ_(1,2) = 2

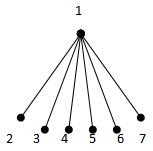{1,2} form a (1,2) - dominating set.

γ_(1,2) = 2

Theorem 4.1

For any star K_1,n, γ_(1,2)(K_1,n) = 2.

Proof:

In a star K_1,n, there are n+1 vertices v, v₁, v₂, ...,v_n. v is adjacent to all other vertices v₁, v₂, ...,v_n. {v₁, v₂, ...,v_n} form an independent set. Each of v₁, v₂, ...,v_n are at a distance 1 from v and each of v₂ , v₃,...,v_n are at a distance 2 from v₁.So we can form a (1,2) dominating set as {v, v₁}. Clearly the cardinality is two. Hence γ_(1,2)(K_1,n) = 2.

5. (1,2) - domination in the Line Graph of P_n, C_n, K_1,n.

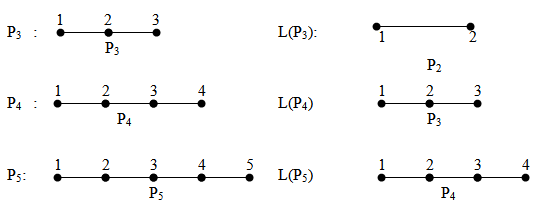
In this section first we discuss the line graphs of paths, cycles and star graphs.

Consider the paths and the corresponding line graphs

Next consider the cycles and the corresponding line graphs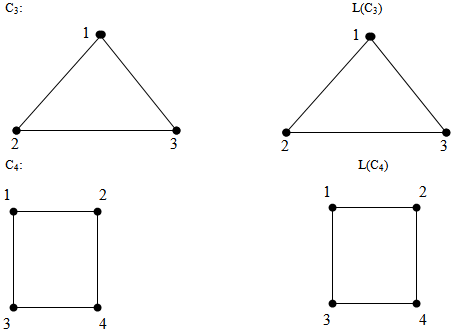

Consider the following star graphs and the corresponding line graphs

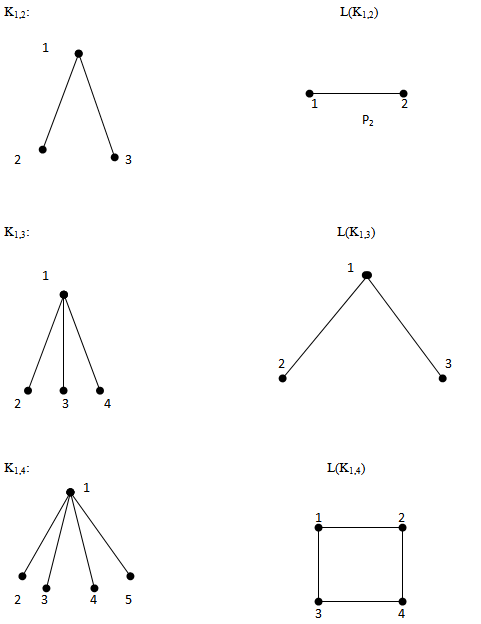From the above examples and from[7] we have the following observations

The line graph of P_n, L(P_n) has

(i) n-1 vertices and n-2 edges

(ii) 2 vertices of degree 1 and n-3 vertices of degree 2.

Hence L(P_n) = P_n-1.

The line graph of C_n has

(i) n vertices and n edges

(ii) Each vertex is of degree 2

(iii) The graph is cyclic

Hence L(C_n)= C_n.

The line graph of K_1,n has

(i) n-1 edges and n vertices

(ii) Each of the n vertices is of degree 2.

(iii) The graph is cyclic

L(K_1,n) = C_n for n ≥ 3.

Theorem 5.1

(1,2) - domination number of L(P_n) is n-3.

Proof :

P_n has n vertices and n-1 edges and L(P_n) is P_n-1 with n-1 vertices and n-2 edges. Then by theorem 2.1, (1,2) - domination number of P_n-1 with n-3. Hence (1,2) - domination in the line graph of L(P_n) is n-3.

Theorem 5.2

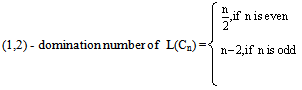Proof:

The line graph of C_n, L(C_n) is C_n itself. So we can apply theorem 3.1

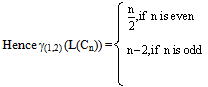Theorem 5.3

(1,2) - domination number of L(K_1,n) is same as that of C_n.

Proof:

The line graph of K_1,n is C_n.

Then by theorem 3.2,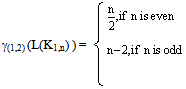

6. Conclusions

In this paper the (1,2)-dominating sets and (1.2) - domination numbers of some standard graphs P_n, C_n and K_1,nhave been discussed and the results extended to the line graphs of those graphs. It is also found that (1,2) - domination number of C_n and K_1,n are same.