Mohamed Houas1, Zoubir Dahmani2
1Department of Mathematics, University of Khemis Miliana, Algeria
2LPAM, Faculty SEI, UMAB Mostaganem, Algeria
Correspondence to: Zoubir Dahmani, LPAM, Faculty SEI, UMAB Mostaganem, Algeria.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
In this paper, we study a four point boundary problem for fractional differential equations. We establish new existence and uniqueness results using the Banach contraction principle. Other existence results are generated using the well known Schaefer’s fixed point theorem. To illustrate our results, we present some examples for the Banach contraction result. Other examples are also treated to illustrate our second main result.
Keywords:
Boundary Value Problem, Caputo Derivative, Fixed Point, Riemann-Liouville Integral
Cite this paper: Mohamed Houas, Zoubir Dahmani, New Results for a Caputo Boundary Value Problem, American Journal of Computational and Applied Mathematics , Vol. 3 No. 3, 2013, pp. 143-161. doi: 10.5923/j.ajcam.20130303.01.
1. Introduction
Boundary value problems for fractional differential equations have been shown to be very useful in the study of models of many phenomena in various fields of applied science and engineering, such as electrochemistry, chemistry, visco‐elasticity, control, biophysics. For more details, we refer the reader to[3, 4, 9, 11, 14, 15, 16, 20] and references therein. Recently, there has been a significant progress in the study of these equations, (see[7, 8, 19]). More recently, some new theories for the initial boundary value problems of fractional differential equations have been discussed in[1, 2, 12, 13 14]. Moreover, existence and uniqueness of solutions to boundary value problems for fractional differential equations has attracted the attention of many authors[6, 7, 8, 14, 17].In[17, 18], the existence and uniqueness of solutions were investigated for a nonlinear fractional differential equation with three‐point boundary conditions by using a Schauder’s fixed point theorem. The existence of solutions for a nonlinear fractional differential equation with four‐point boundary conditions was investigated in[5, 10] by using Schauder’s fixed point.Motivated by the problem (1) in[20], this paper deals with the existence and uniqueness of solutions for the following problem: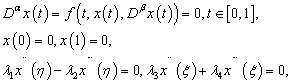 | (1.1) |
where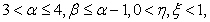 and
and 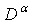 and
and 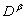 are the Caputo fractional derivatives,
are the Caputo fractional derivatives, 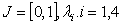 are real constants with
are real constants with 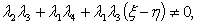 and
and 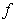 is a continuous function on
is a continuous function on 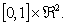 The paper is organized as follows. In section 2, we present some preliminaries and lemmas. In Section 3, we prove the main results of this work. In section 4, we will give some examples to illustrate our results.
The paper is organized as follows. In section 2, we present some preliminaries and lemmas. In Section 3, we prove the main results of this work. In section 4, we will give some examples to illustrate our results.
2. Preliminaries
The following notations, definitions, and preliminary facts will be used throughout this paper.Definition 1: The Riemann-Liouville fractional integral operator of order 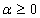 , for a continuous function
, for a continuous function 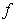 on
on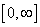 is defined as:
is defined as: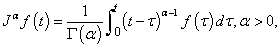 | (2.1) |
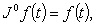 where
where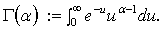 Definition 2: The fractional derivative of
Definition 2: The fractional derivative of 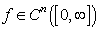 in the sense of Caputo is defined as:
in the sense of Caputo is defined as: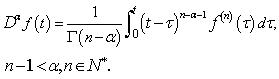 | (2.2) |
For more details, we refer the reader to[14, 16].Let us now introduce the following Banach space 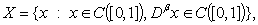 endowed with the norm
endowed with the norm 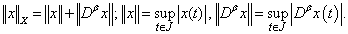 We give the following lemmas[11]:Lemma 3: For
We give the following lemmas[11]:Lemma 3: For 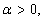 the general solution of the fractional differential equation
the general solution of the fractional differential equation 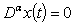 is given by
is given by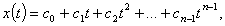 | (2.3) |
where 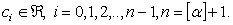 Lemma 4: Let
Lemma 4: Let 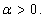 Then
Then 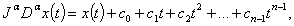 | (2.4) |
for some 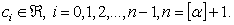 We give also the following result:Lemma 5: Let
We give also the following result:Lemma 5: Let 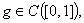 the solution of the equation
the solution of the equation 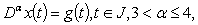 | (2.5) |
subject to the boundary conditions 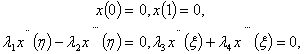 | (2.6) |
is given by: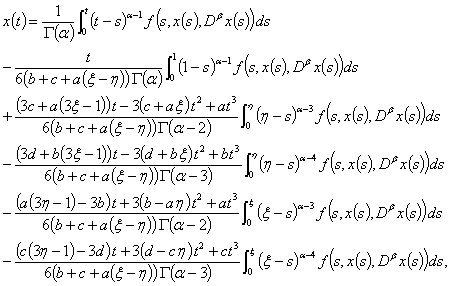 | (2.7) |
where 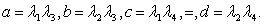 Proof. For
Proof. For 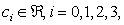 and by lemmas 3, 4, the general solution of (2.5) is given by
and by lemmas 3, 4, the general solution of (2.5) is given by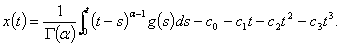 | (2.8) |
Using the boundary conditions (2.6), we obtain 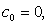
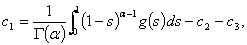 and
and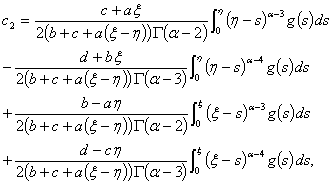 | (2.9) |
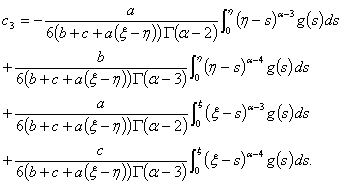 | (2.10) |
Substituting the values of 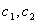 and
and 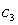 in (2.8), we obtain the desired relation in Lemma 5.
in (2.8), we obtain the desired relation in Lemma 5.
3. Main Results
We introduce the following quantities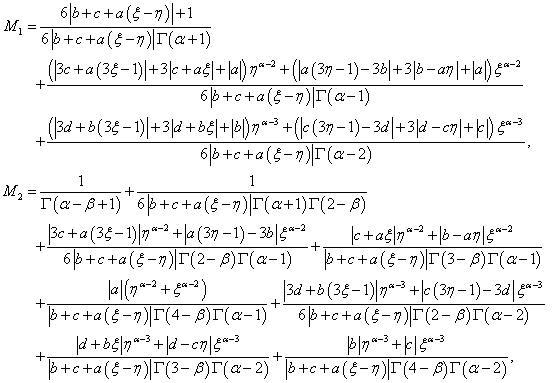 | (3.1) |
and we list the following hypotheses:(H1): The function 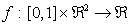 is continuous.(H2): There exist non negative continuous functions
is continuous.(H2): There exist non negative continuous functions 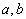 , on
, on 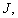 such that for
such that for 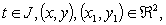 we have
we have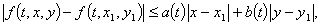 | (3.2) |
where, 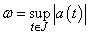 and
and 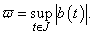 (H3): There exists
(H3): There exists 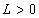 such that
such that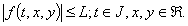 | (3.3) |
Our first result is based on the Banach contraction principle. We have:Theorem 6: Assume that the hypothesis (H2) holds.If 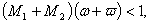 | (3.4) |
then the problem (1.1) has a unique solution on 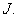 Proof. Consider the operator
Proof. Consider the operator 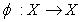 defined by:
defined by: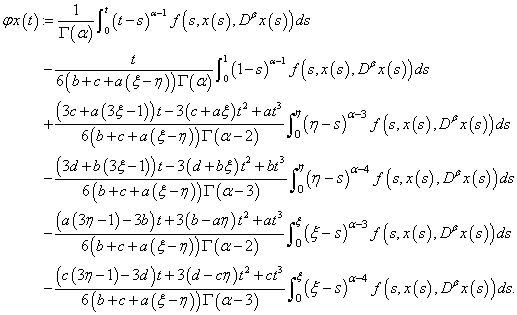 | (3.5) |
We shall prove that 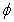 is a contraction:For
is a contraction:For 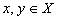 and
and 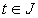 , we obtain
, we obtain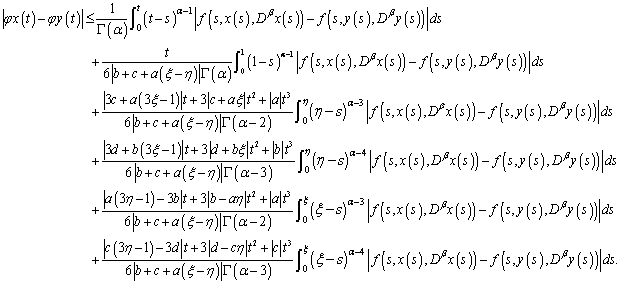 | (3.6) |
Using (H2), we can write: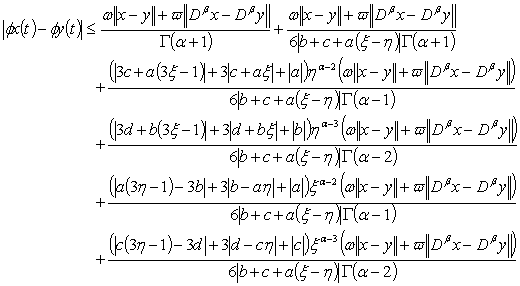 | (3.7) |
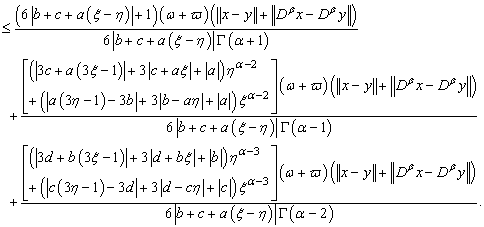 Consequently, we obtain,
Consequently, we obtain,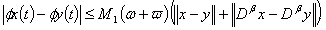 | (3.8) |
Hence, we have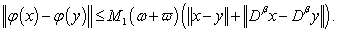 | (3.9) |
On the other hand,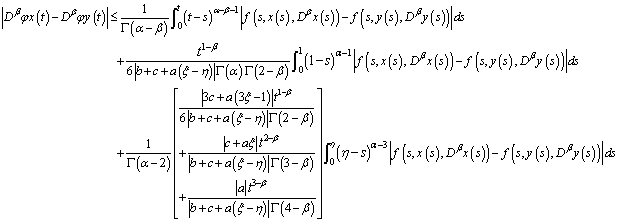
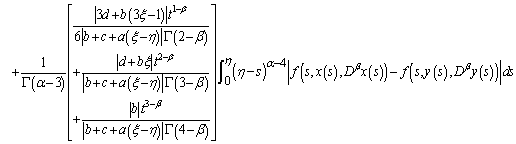 | (3.10) |
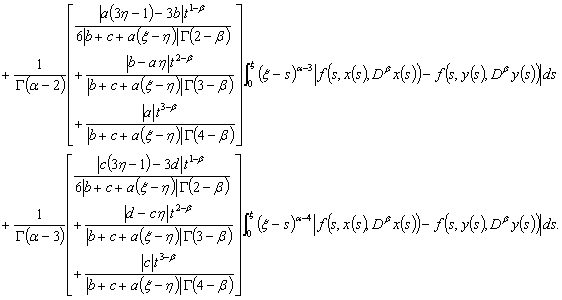 By
By 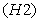 , we obtain
, we obtain
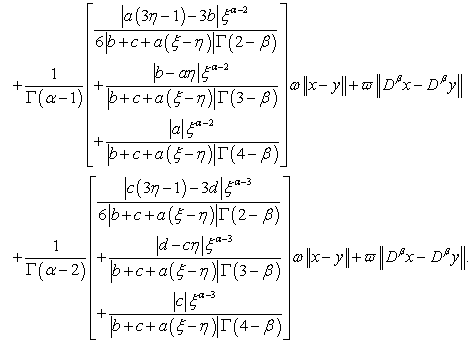 | (3.11) |
Hence, | (3.12) |
Therefore,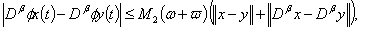 | (3.13) |
which implies,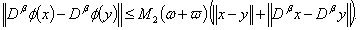 | (3.14) |
It follows from (3.9) and (3.14) that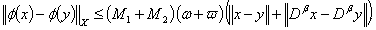 | (3.15) |
Thanks to (3.4), we deduce that 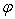 is a contraction. As a consequence of Banach contraction principle, the problem (1.1) has a unique solution on
is a contraction. As a consequence of Banach contraction principle, the problem (1.1) has a unique solution on 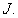 The second result is based on Scheafer's fixed point theorem.Theorem 7: Suppose that (H1) and (H3) hold.Then, the problem (1.1) has at least one solution on
The second result is based on Scheafer's fixed point theorem.Theorem 7: Suppose that (H1) and (H3) hold.Then, the problem (1.1) has at least one solution on 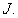 Proof. We use Scheafer's fixed point theorem to prove that
Proof. We use Scheafer's fixed point theorem to prove that 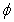 has at least a fixed point on
has at least a fixed point on 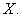 The proof will be given in following steps:Step1:
The proof will be given in following steps:Step1: 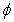 is continuous on
is continuous on 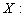 In view of the continuity of
In view of the continuity of 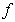 , we conclude that the operator
, we conclude that the operator 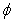 is continuous.Step2: The operator
is continuous.Step2: The operator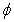 maps bounded sets into bounded sets in
maps bounded sets into bounded sets in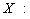 For
For 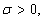 we take
we take 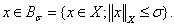 For
For 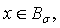 and
and 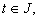 we can write:
we can write: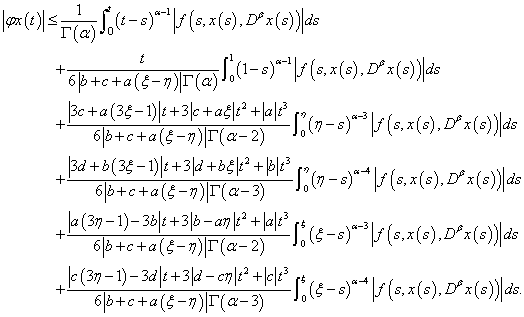 | (3.16) |
Using (H3), we can write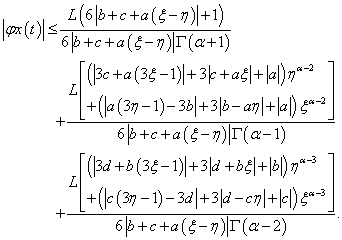 | (3.17) |
Thus,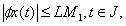 | (3.18) |
which implies that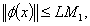 | (3.19) |
and | (3.20) |
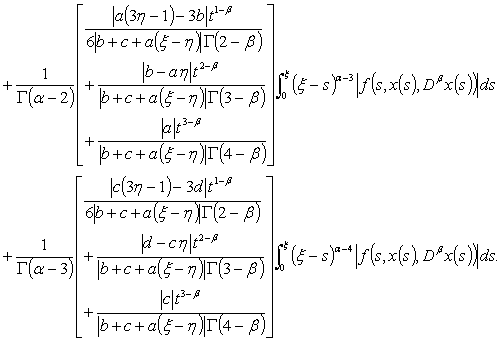 By (H3) , yields
By (H3) , yields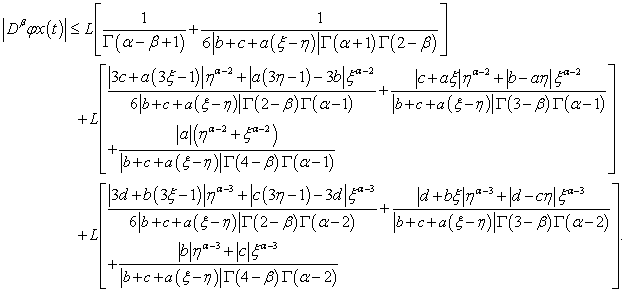 | (3.21) |
Hence,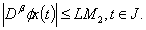 | (3.22) |
And consequently,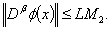 | (3.23) |
Thanks to (3.19) and (3.23), we obtain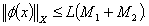 | (3.24) |
Therefore,Step 3: The operator 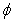 is equicontinuous on X:Let us take
is equicontinuous on X:Let us take 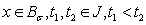 . We have:
. We have: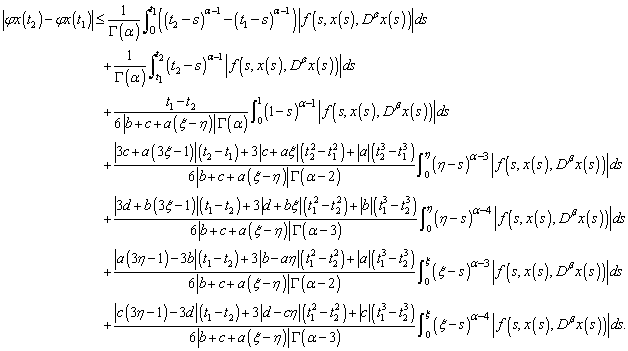 | (3.25) |
Thanks to (H3), we can write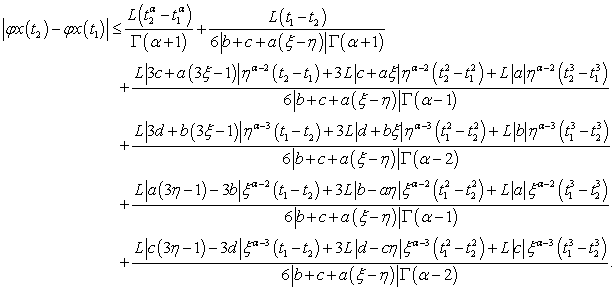 | (3.26) |
Then,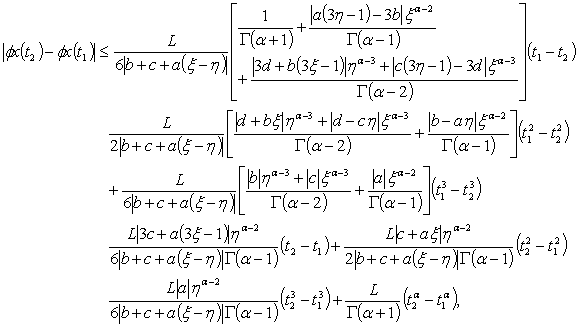 | (3.27) |
we have also,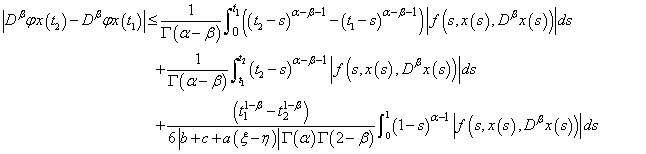
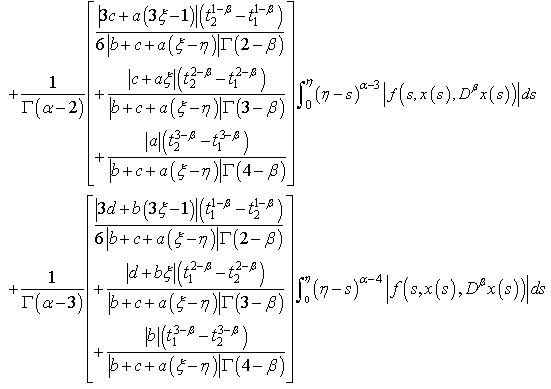
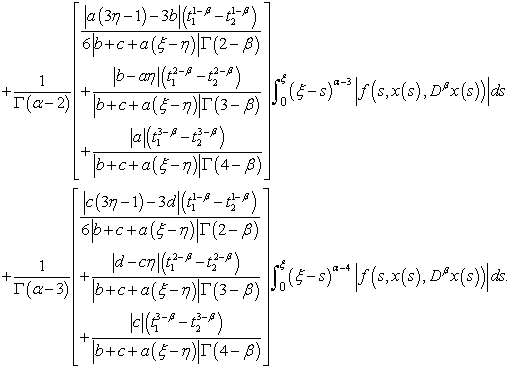 | (3.28) |
By (H3), we obtain: | (3.29) |
Hence, from (3.27) and (3.29), we get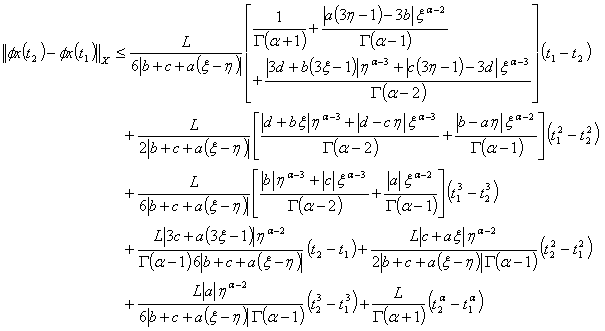
 | (3.30) |
which implies 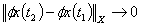 as
as 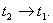 By Arzela-Ascoli theorem, we conclude that
By Arzela-Ascoli theorem, we conclude that 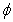 is completely continuous operator. Step 4: We show that the set
is completely continuous operator. Step 4: We show that the set 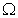 defined by:
defined by: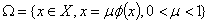 | (3.31) |
is bounded:Let 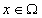 , then
, then 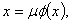 for some
for some 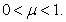 Thus, for each
Thus, for each 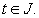 we have:
we have: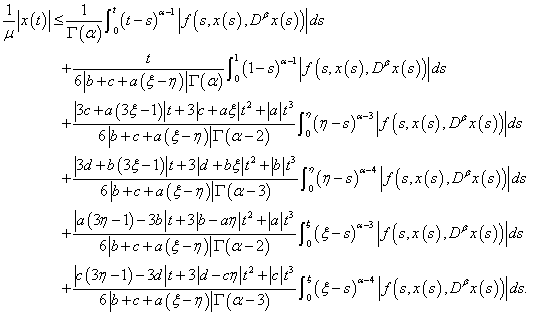 | (3.32) |
Thanks to (H3), we can write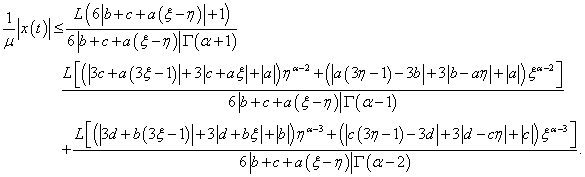 | (3.33) |
Therefore,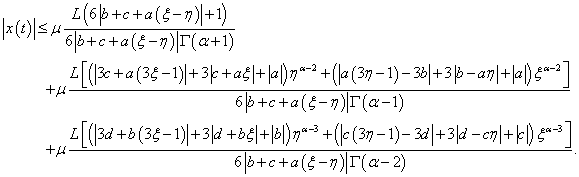 | (3.34) |
Thus,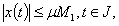 | (3.35) |
which implies that,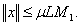 | (3.36) |
On the other hand,  | (3.37) |
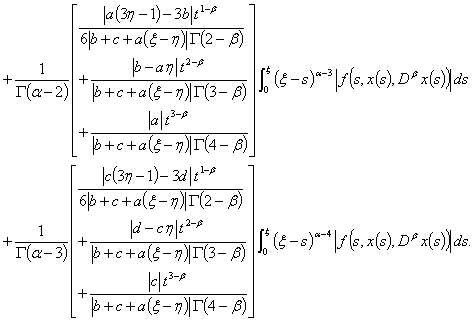 By (H3), we have,
By (H3), we have,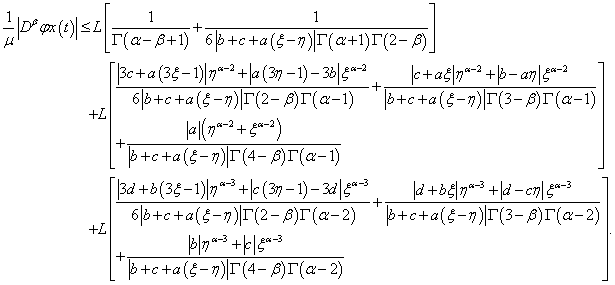 | (3.38) |
Therefore,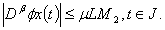 | (3.39) |
Thus,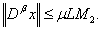 | (3.40) |
From (3.36) and (3.40), we get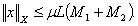 | (3.41) |
Hence,This shows that 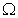 is bounded.As consequence of Schaefer's fixed point theorem, the problem (1.1) has at least one solution on J.
is bounded.As consequence of Schaefer's fixed point theorem, the problem (1.1) has at least one solution on J.
4. Examples
Examlpe 1: Consider the following problem: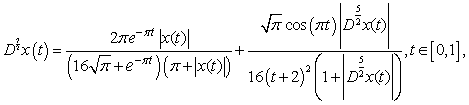 | (4.1) |
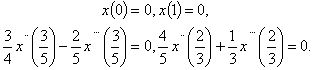 For this example, we have
For this example, we have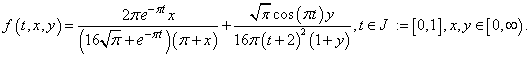 Let
Let 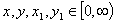 and
and 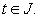 Then we can state that:
Then we can state that: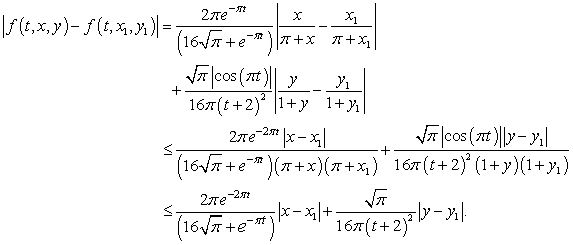 So we can take
So we can take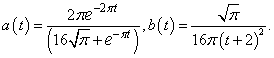 Therefore,
Therefore, 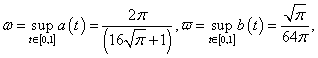 and then,
and then,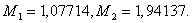 We have also
We have also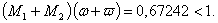 Hence by Theorem 6, the problem (4.1) has a unique solution on
Hence by Theorem 6, the problem (4.1) has a unique solution on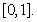 Example 2: Consider the following problem:
Example 2: Consider the following problem: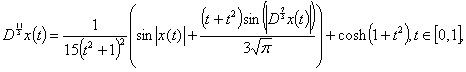
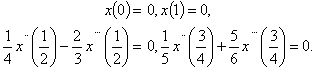 | (4.2) |
Set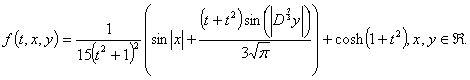 For
For 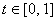 and
and 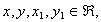 we have:
we have: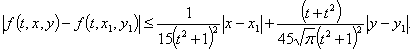 So, we have
So, we have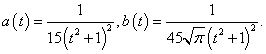 Hence,
Hence,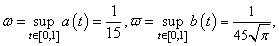
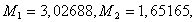 and
and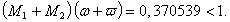 By Theorem6, the problem (4.2) has a unique solution on
By Theorem6, the problem (4.2) has a unique solution on 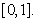 Example 3: Our third example is the following:
Example 3: Our third example is the following: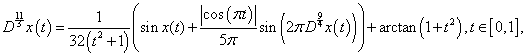
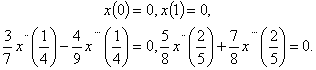 | (4.3) |
For this example, we have: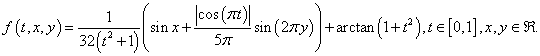 It is clear that f is continuous, and there exists
It is clear that f is continuous, and there exists 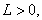 such that
such that 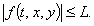 By theorem 7, we can state that the problem (4.3) has at least one solution on
By theorem 7, we can state that the problem (4.3) has at least one solution on 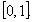 Example 4: We give also the following example:
Example 4: We give also the following example: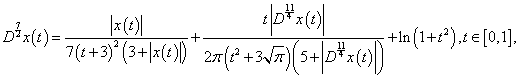
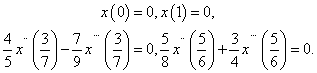 | (4.4) |
It is clear that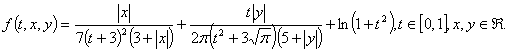 The conditions (H1) and (H3) of Theorem7 are satisfied. Therefore the problem (4.4) has at least one solution on
The conditions (H1) and (H3) of Theorem7 are satisfied. Therefore the problem (4.4) has at least one solution on 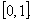
5. Conclusions
In this paper, we have studied a four point boundary problem for fractional differential equations in the sense of Caputo. By using Banach contraction principle, we have established new sufficient conditions for the existence and uniqueness of solutions for the problem (1.1). Other existence results are generated using the well known Schaefer’s fixed point theorem. Furthermore, to illustrate our main results, we have treated two examples related to the Banach contraction result. We have also studied two other examples for our second main result.
References
| [1] | B. Ahmad, A. Afrah: Existence results for Caputo type fractional differential equations with four-point nonlocal fractional integral boundary conditions. Electronic Journal of Qualitative Theory of Differential Equations. 93, pp.1-11, 2012. |
| [2] | B. Ahmad, SK. Ntouyas: A four-point nonlocal integral boundary value problem for fractional differential equations of arbitrary order. Electronic Journal of Qualitative Theory of Differential Equations. 22,pp.1-15, 2011. |
| [3] | Z. Bai, Y. Zhang: Solvability of fractional three-point boundary value problems with nonlinear growth. Appl. Math.Comput. 218(5), pp. 1719-1725, 2011. |
| [4] | M.E. Bengrine, Z. Dahmani: Boundary value problems for fractional differential equations. Int. J. Open problems Compt. Math. 5(4), 2012. |
| [5] | Z. Cui, P. Yu and Z. Mao: Existence of solutions for nonlocal boundary value problems of nonlinear fractional differential equations. Advances in Dynamical Systems and Applications. 7(1), pp. 31-40, 2012. |
| [6] | D. Delbosco, L. Rodino: Existence and uniqueness for a nonlinear fractional differential equation. J. Math. Anal. Appl. 204 (3-4), pp. 429-440, 1996. |
| [7] | K. Diethelm, G. Walz: Numerical solution of fraction order differential equations by extrapolation. Numer. Algorithms. 16(3), pp. 231-253, 1998. |
| [8] | A.M.A. El-Sayed: Nonlinear functional differential equations of arbitrary orders. Nonlinear Anal. 33(2), pp. 181-186, 1998. |
| [9] | M. Houas, Z. Dahmani: New fractional results for a boundary value problem with Caputo derivative. (Paper Accepted in IJOPCM Journal of Open Problems, 2013). |
| [10] | M. Houas, Z. Dahmani, M. Benbachir: New results for differential equations of arbitrary order. IJMMS Journal. In press. |
| [11] | A.A. Kilbas, S.A. Marzan: Nonlinear differential equation with the Caputo fraction derivative in the space of continuously differentiable functions, Differ. Equ. 41(1), pp. 84-89, 2005. |
| [12] | V. Lakshmikantham, A.S. Vatsala: Basic theory of fractional differential equations. Nonlinear Anal. 69(8), pp. 2677-2682, 2008. |
| [13] | C. Li, X. Luo, Y. Zhou: Existence of positive solutions of the boundary value problem for nonlinear fractional differential equations. Comput. Math. Appl. 59, pp. 1363-1375, 2010. |
| [14] | F. Mainardi, Fractional calculus: Some basic problem in continuum and statistical mechanics. Fractals and fractional calculus in continuum mechanics, Springer, Vienna. (1997). |
| [15] | S.K. Ntouyas: Existence results for first order boundary value problems for fractional differential equations and inclusions with fractional integral boundary conditions. Journal of Fractional Calculus and Applications. 3(9), pp. 1-14, 2012. |
| [16] | I. Podlubny, I. Petras, B.M. Vinager, P. O'leary, L. Dorcak: Analogue realizations of fractional-order controllers. Fractional order calculus and its applications. Nonlinear Dynam. 29(4), pp. 281-296, 2002. |
| [17] | M.U. Rehman,R.A, Khan, N.A. Asif: Three point boundary value problems for nonlinear fractional differential equations. Acta Mathematica Scientia. 31B(4), pp. 1337-1346, 2011. |
| [18] | W. Sudsutad, J. Tariboon: Boundary value problems for fractional differential equations with three-point fractional integral boundary conditions. Advances in Difference Equations. 93, 2012. |
| [19] | S. Zhang: Positive solutions for boundary-value problems of nonlinear fractional differential equations. Electron. J. Differential Equations. 2(36), pp. 12-19, 2006. |
| [20] | Q. Zhang, S. Chen, J. Lü: Upper and lower solution method for fourth-order four-point boundary value problems, Journal of Computational and Applied Mathematics. 196, pp. 387-393, 2006. |

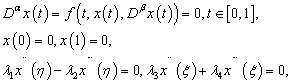
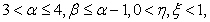 and
and 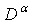 and
and 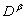 are the Caputo fractional derivatives,
are the Caputo fractional derivatives, 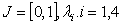 are real constants with
are real constants with 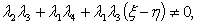 and
and 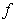 is a continuous function on
is a continuous function on 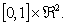 The paper is organized as follows. In section 2, we present some preliminaries and lemmas. In Section 3, we prove the main results of this work. In section 4, we will give some examples to illustrate our results.
The paper is organized as follows. In section 2, we present some preliminaries and lemmas. In Section 3, we prove the main results of this work. In section 4, we will give some examples to illustrate our results.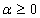 , for a continuous function
, for a continuous function 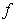 on
on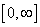 is defined as:
is defined as: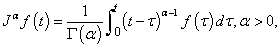
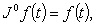 where
where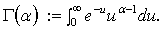 Definition 2: The fractional derivative of
Definition 2: The fractional derivative of 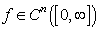 in the sense of Caputo is defined as:
in the sense of Caputo is defined as: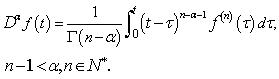
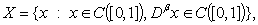 endowed with the norm
endowed with the norm 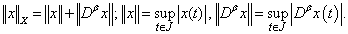 We give the following lemmas[11]:Lemma 3: For
We give the following lemmas[11]:Lemma 3: For 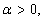 the general solution of the fractional differential equation
the general solution of the fractional differential equation 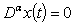 is given by
is given by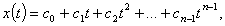
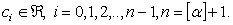 Lemma 4: Let
Lemma 4: Let 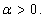 Then
Then 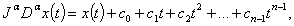
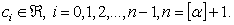 We give also the following result:Lemma 5: Let
We give also the following result:Lemma 5: Let 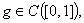 the solution of the equation
the solution of the equation 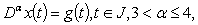
 Proof. For
Proof. For  and by lemmas 3, 4, the general solution of (2.5) is given by
and by lemmas 3, 4, the general solution of (2.5) is given by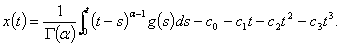
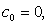
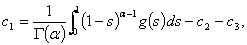 and
and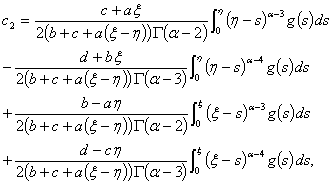
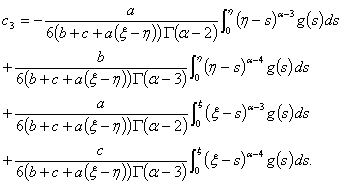
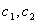 and
and 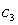 in (2.8), we obtain the desired relation in Lemma 5.
in (2.8), we obtain the desired relation in Lemma 5.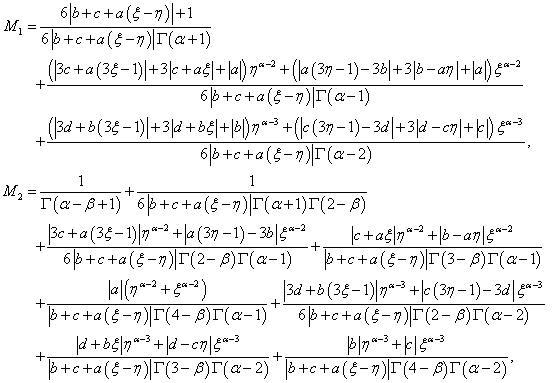
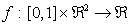 is continuous.(H2): There exist non negative continuous functions
is continuous.(H2): There exist non negative continuous functions 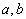 , on
, on 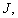 such that for
such that for 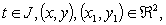 we have
we have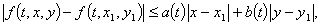
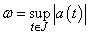 and
and 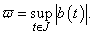 (H3): There exists
(H3): There exists 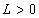 such that
such that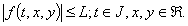
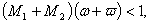
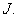 Proof. Consider the operator
Proof. Consider the operator 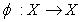 defined by:
defined by: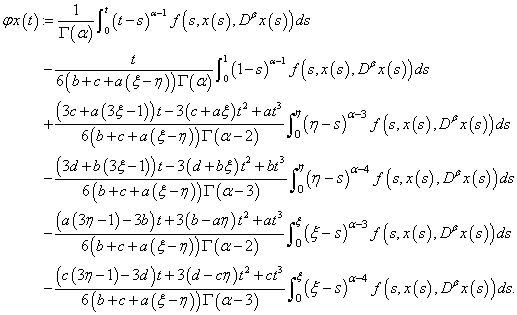
 is a contraction:For
is a contraction:For  and
and  , we obtain
, we obtain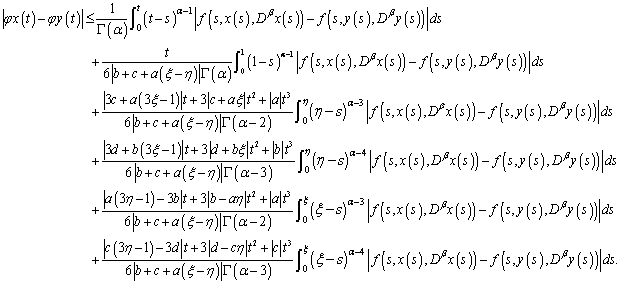
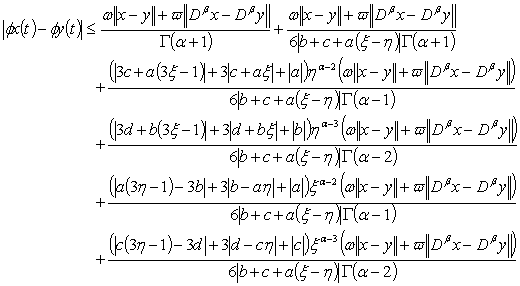
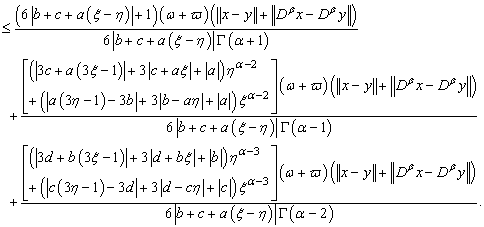 Consequently, we obtain,
Consequently, we obtain,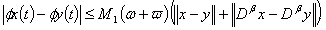
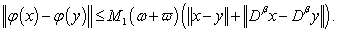
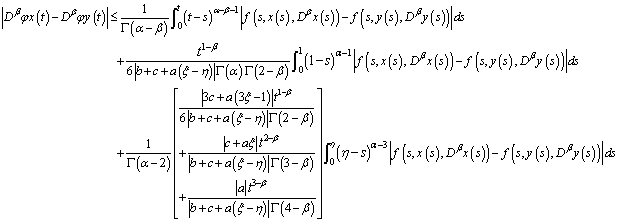
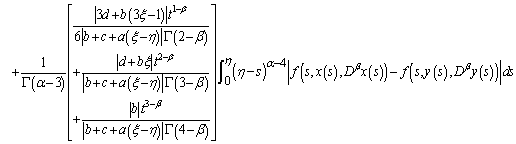
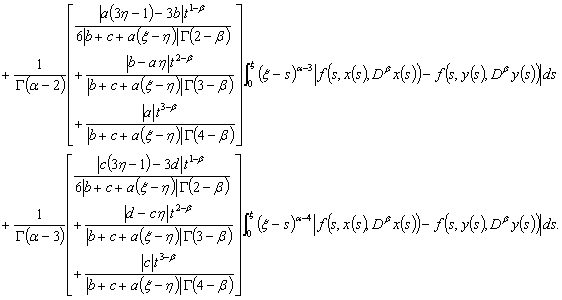 By
By 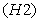 , we obtain
, we obtain
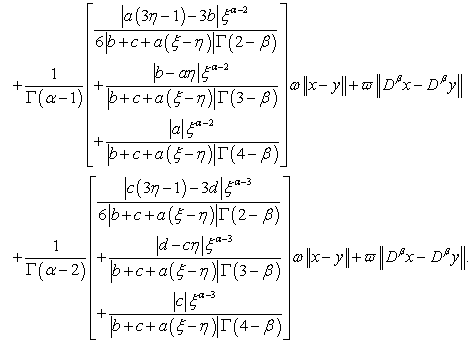

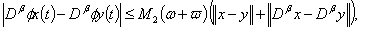
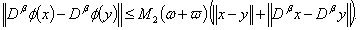
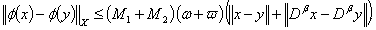
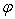 is a contraction. As a consequence of Banach contraction principle, the problem (1.1) has a unique solution on
is a contraction. As a consequence of Banach contraction principle, the problem (1.1) has a unique solution on  The second result is based on Scheafer's fixed point theorem.Theorem 7: Suppose that (H1) and (H3) hold.Then, the problem (1.1) has at least one solution on
The second result is based on Scheafer's fixed point theorem.Theorem 7: Suppose that (H1) and (H3) hold.Then, the problem (1.1) has at least one solution on  Proof. We use Scheafer's fixed point theorem to prove that
Proof. We use Scheafer's fixed point theorem to prove that 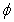 has at least a fixed point on
has at least a fixed point on 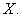 The proof will be given in following steps:Step1:
The proof will be given in following steps:Step1: 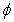 is continuous on
is continuous on 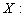 In view of the continuity of
In view of the continuity of 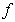 , we conclude that the operator
, we conclude that the operator 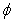 is continuous.Step2: The operator
is continuous.Step2: The operator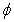 maps bounded sets into bounded sets in
maps bounded sets into bounded sets in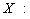 For
For 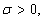 we take
we take 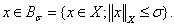 For
For 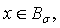 and
and 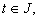 we can write:
we can write: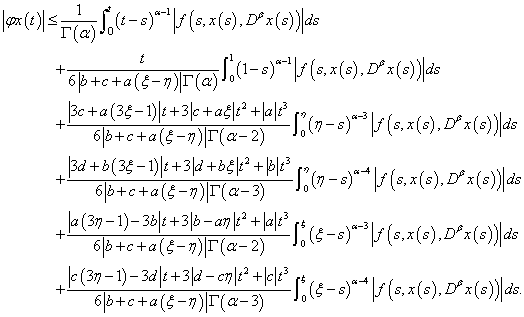
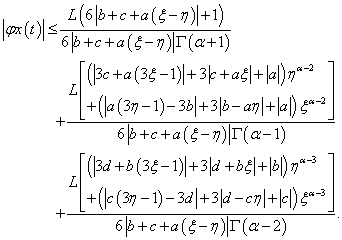
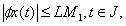
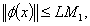

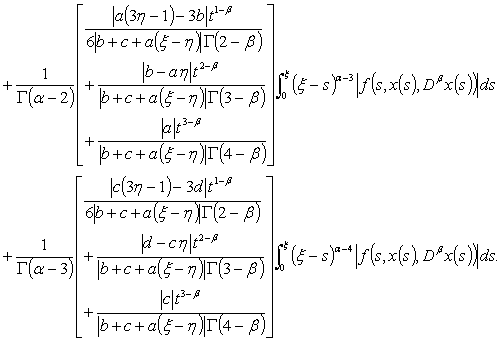 By (H3) , yields
By (H3) , yields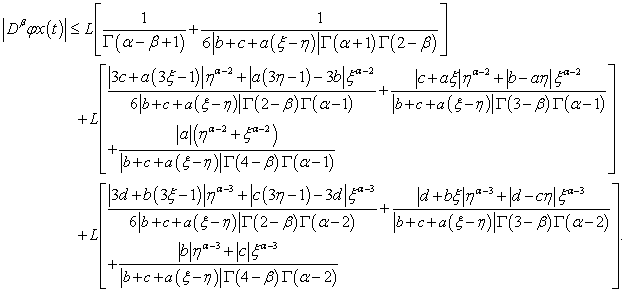
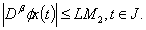
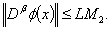
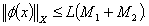
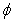 is equicontinuous on X:Let us take
is equicontinuous on X:Let us take 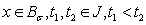 . We have:
. We have: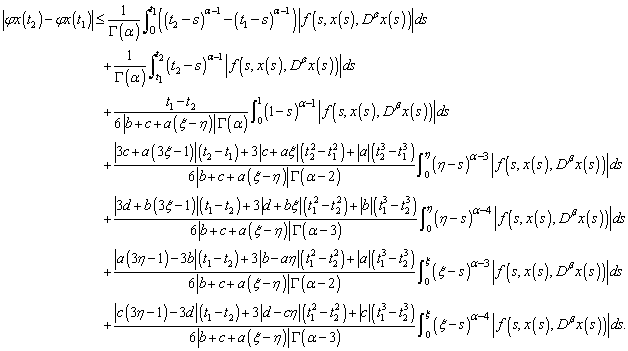
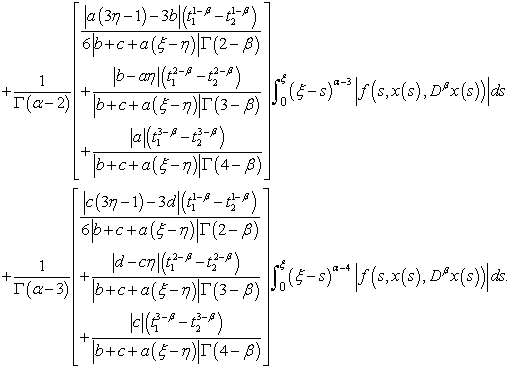

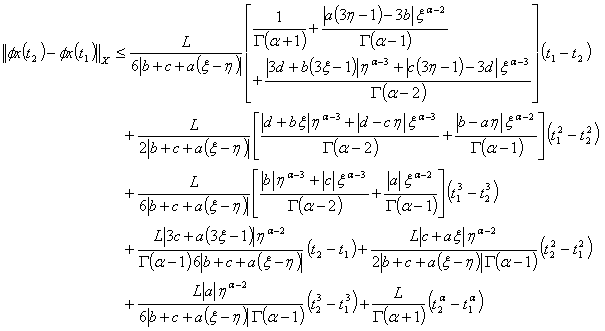

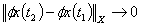 as
as 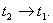 By Arzela-Ascoli theorem, we conclude that
By Arzela-Ascoli theorem, we conclude that 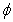 is completely continuous operator. Step 4: We show that the set
is completely continuous operator. Step 4: We show that the set 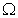 defined by:
defined by: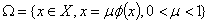
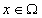 , then
, then 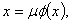 for some
for some 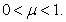 Thus, for each
Thus, for each  we have:
we have: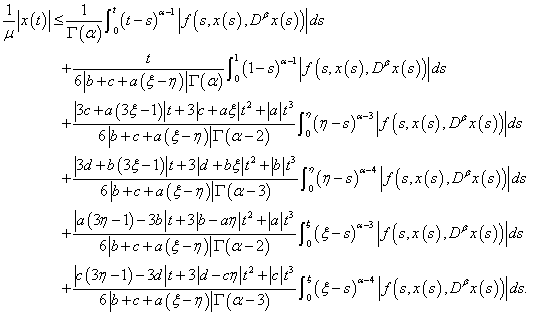
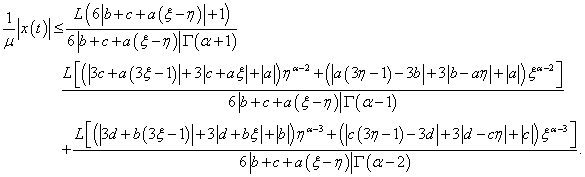
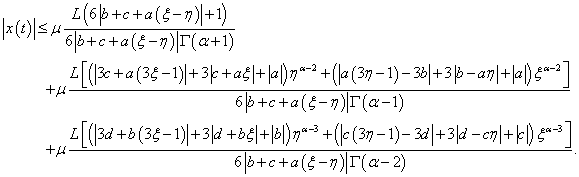
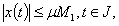
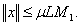

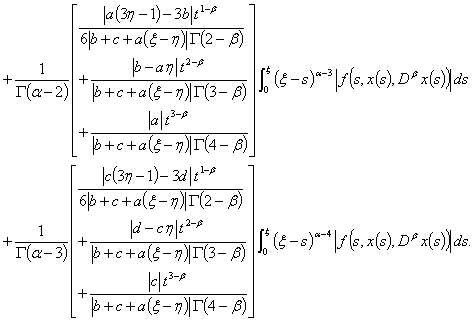 By (H3), we have,
By (H3), we have,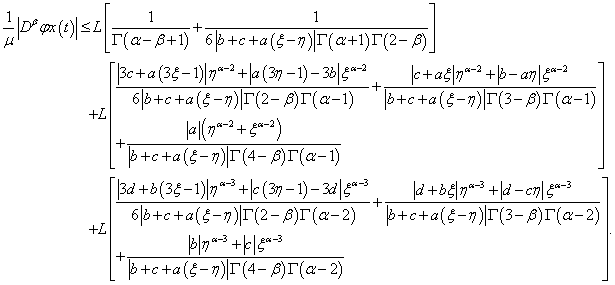
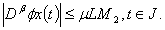
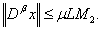
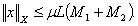
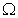 is bounded.As consequence of Schaefer's fixed point theorem, the problem (1.1) has at least one solution on J.
is bounded.As consequence of Schaefer's fixed point theorem, the problem (1.1) has at least one solution on J.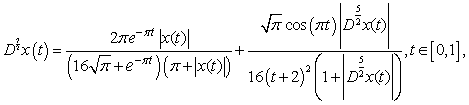
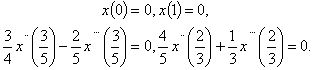 For this example, we have
For this example, we have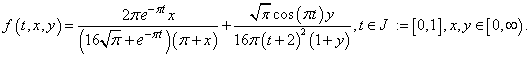 Let
Let 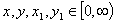 and
and 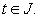 Then we can state that:
Then we can state that: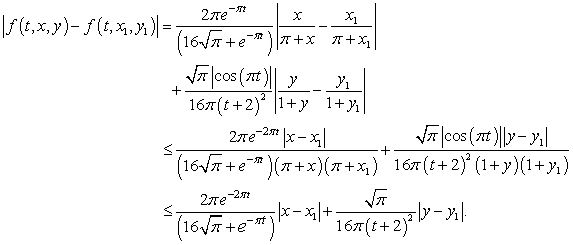 So we can take
So we can take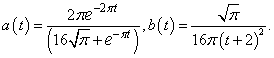 Therefore,
Therefore, 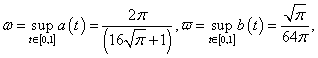 and then,
and then,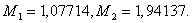 We have also
We have also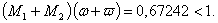 Hence by Theorem 6, the problem (4.1) has a unique solution on
Hence by Theorem 6, the problem (4.1) has a unique solution on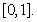 Example 2: Consider the following problem:
Example 2: Consider the following problem: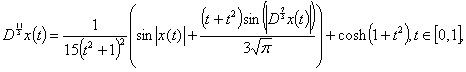
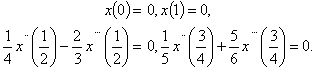
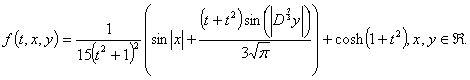 For
For 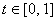 and
and 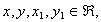 we have:
we have: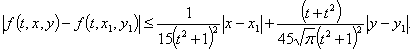 So, we have
So, we have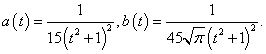 Hence,
Hence,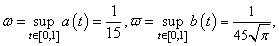
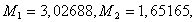 and
and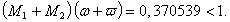 By Theorem6, the problem (4.2) has a unique solution on
By Theorem6, the problem (4.2) has a unique solution on 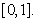 Example 3: Our third example is the following:
Example 3: Our third example is the following: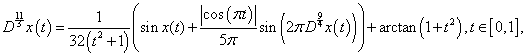
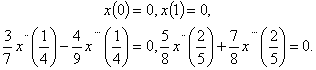
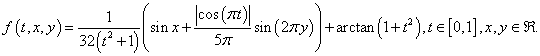 It is clear that f is continuous, and there exists
It is clear that f is continuous, and there exists  such that
such that 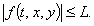 By theorem 7, we can state that the problem (4.3) has at least one solution on
By theorem 7, we can state that the problem (4.3) has at least one solution on  Example 4: We give also the following example:
Example 4: We give also the following example: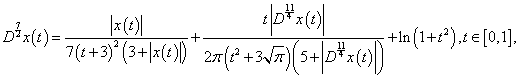
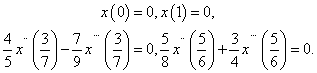
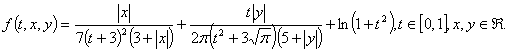 The conditions (H1) and (H3) of Theorem7 are satisfied. Therefore the problem (4.4) has at least one solution on
The conditions (H1) and (H3) of Theorem7 are satisfied. Therefore the problem (4.4) has at least one solution on 
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML