| [1] | W. Malfiet, the tanh method I: Exact solutions of nonlinear evolution and wave equations , American Journal of Physics, Vol. 4, PP. 650-654, 1992.. |
| [2] | W. Malfiet, W. Hereman, The tanh method I: Exact solutions of nonlinear evolution and wave equations, Physica Scripta, , Vol. 54 , PP. 563-568, 1996. |
| [3] | A. M. Wazwaz, The tanh and the sine-cosine methods for the complex modified KdV and the generalized KdV equations, Applied Mathematics and Computations, Vol. 154, PP. 713-723, 2004. |
| [4] | E. Fan, C. H. Zhang, A note on the homogeneous balance method, Physics Letters, Vol. A246, PP. 403-406, 1998. |
| [5] | E. Fan, Two new applications of the homogeneous balance method, Physics Letters Vol. A265, PP. 353-357, 2000. |
| [6] | M. Senthilvelan, On the extended applications of homogeneous balance method, Applied Mathematics and Computions, Vol. 123, PP. 381-388, 2001. |
| [7] | M. L. Wang, Exact solutions of a compound KdV- Burgers equation, Physics Letters Vol. A213, PP. 279-287, 1996. |
| [8] | E. Fan, Extended tanh-function method and its applications to nonlinear equations, Phys. Lett. A277(2000)212-218. |
| [9] | E. Fan, Y. C. Hon, Applications of extended tanh method to “special” types of nonlinear equations, AppliedMathematics and. Computions, Vol. 141, PP. 351-358, 2003. |
| [10] | A. M. Wazwaz, the tanh-coth and the sine-cosine methods for kinks, solitons and periodic solutions for the pochhammer- Chree equations, Appl.ied Mathematics and Computations, Vol. 195, PP. 24-33, 2008. |
| [11] | A. Ebaid, Exact solitary wave solutions for some nonlinear evolution equations via Exp-function method, Journal of Physics A: Math.ematical Theories, Vol. 34 , PP. 305-317, 2000. |
| [12] | J. H. He, X. H. Wu, Exp-function method for nonlinear wave equations, Chaos Solitons and Fractals, Vol. 30 , PP. 700-708, 2006. |
| [13] | J. H. He, M. A. Abdou, New periodic solutions for nonlinear evolution equations using Exp-function method, Chaos solitons and Fractals, Vol. 34, PP. 1421-1429, 2007. |
| [14] | X. H. Wu, J. H. H, Exp- function method and its application to nonlinear equations, Chaos Solitons and Fract.als, Vol. 38, PP. 903-910, 2008. |
| [15] | S. Zhang, Application of Exp-function method to a KdV equation with variable coefficients, Physics Letters, Vol. A365, PP. 448-453, 2007. |
| [16] | E. Fan, J. Zhang, Applications of the Jacobi elliptic function method to special-type nonlinear equations, Phys.ics Letters, Vol. A305, PP. 383-392, 2002. |
| [17] | S. Liu, Z. Fu, S. Liu, Q. Zhao, Jacobi elliptic function method and periodic wave solutions of nonlinear wave equations, Physics Letters, Vol. A289 , PP. 69-74, 2001. |
| [18] | M. A. Abdou, The extended F-expansion method and its applications for a class of nonlinear evolution equations, Chaos Soliton and Fractals, Vol. 31 , PP. 95-104, 2007. |
| [19] | Y. J. Ren, S. T, Liu, H. Q. Zhang, On a generalized improved F-expansion method, Communications in theoretical Physics. Phys. ( Beijing, China), Vol. 45, PP. 15-28, 2006. |
| [20] | J. L. Zhang, M. L. Wang, Y. M. Wang, Z. D. Fang, The improved F. expansion method and its applications, Physics Letters, Vol. A350, PP. 103-109, 2006. |
| [21] | A. M. Wazwaz, The tanh method for traveling wave solutions of nonlinear equations, Applied Mathematics andComputations, Vol. 133, PP. 213-227, 2002. |
| [22] | Djeumen Tchaho Clovis Taki, Jean Roger Bogning and Timoléon Crépin Kofane. Construction of the analytical solitary wave solutions of modified Kuramoto-Sivashinsky’s equation by the method of identification of coefficients of the hyperbolic functions, Far East Journal of Dynamical Systems, Vol. 14(1), PP. 17-34, 2010. |
| [23] | Djeumen Tchaho Clovis Taki, Jean Roger Bogning and Timoléon Crépin Kofane. Multi-Soliton solutions of the modified Kuramoto- Sivashinsky’s equation by the BDK method, Far East Journal of Dynamical Systems, Vol. 15(1), PP. 83-98. |
| [24] | J. R. Bogning, C. T. Djeumen Tchaho , T. C. Kofané, Construction of the soliton solutions of the Ginzburg-Landau equations by the new Bogning-Djeumen Tchaho-Kofané method, Physica Scripta, Vol. 85, PP. 025013-025018, 2012. |
| [25] | Jean Roger Bogning, Clovis T Djeumen Tchaho, Timoléon C Kofane, Generalization of the Bogning- DjeumenTchaho-Kofane method for the construction of the solitary waves and the survey of the instabilities, Far East Journal of Dynamical Systems, Vol. 20(2), PP. 101-119, 2012.. |
| [26] | Clovis Taki Djeumen Tchaho, J. R. Bogning and T. C. Kofané, Modulated Soliton Solution of the Modified Kuramoto Sivashinsky's Equation, American Journal of Computational and Applied Mathematics, Vol.. 2(5), PP. 218-224. |
| [27] | N. Sasa and J. Satsuma. New type of soliton solutions for a higher-order nonlinear Schrödinger equation, Journal of the Physical Society of Japan, Vol. 60, PP. 408-417, 1991. |
| [28] | S. Ghosh, A. Kundu and S. Nandy. Solitons solutions Liouville integrability and gauge equivalence of Sasa-Satsuma equation, Journal of. Mathematical Physics, Vol. 40, PP. 1993-2000, 1999. |

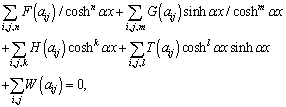
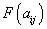 ,
, 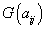 ,
, 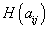 ,
, 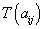 and
and 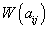 are functions of the coefficients to determine.The paper is organized as follows: In section 2 , we look for the ranges of equations, in section 3, we solve the obtained ranges of equations and in section 4, we conclude the work.
are functions of the coefficients to determine.The paper is organized as follows: In section 2 , we look for the ranges of equations, in section 3, we solve the obtained ranges of equations and in section 4, we conclude the work. 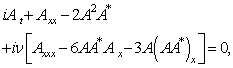
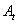 represents the first derivative of the envelope
represents the first derivative of the envelope 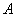 with respect to time,
with respect to time, 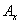 represents the first derivative of the envelope
represents the first derivative of the envelope 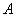 with respect to variable
with respect to variable 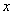 and
and 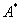 stands for a conjugate complex of
stands for a conjugate complex of 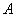 . We propose to construct a solution made up of a combination of analytic forms of solitary waves. Not knowing the exact form capable of producing good results, we opt for the construction of the solution of the form
. We propose to construct a solution made up of a combination of analytic forms of solitary waves. Not knowing the exact form capable of producing good results, we opt for the construction of the solution of the form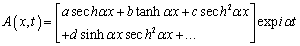
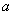 ,
, 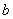 ,
, 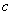 ,
, 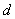 and
and 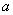 can be real or complex. Given that the choice of the exact solution form of equation (2) is not always easy, we suppose that all the coefficients are complexes such that
can be real or complex. Given that the choice of the exact solution form of equation (2) is not always easy, we suppose that all the coefficients are complexes such that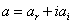 ,
, 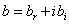 ,
, 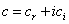 ,
, 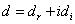 and where
and where 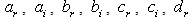 ,
, 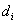 and
and 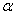 are real constants and
are real constants and 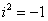 . The choice of the solution in this form permits to have maximum possibilities as regard to the choice of the form of equation (3) which verifies best equation (2). Considering this, the introduction of equation (3) in equation (2) gives
. The choice of the solution in this form permits to have maximum possibilities as regard to the choice of the form of equation (3) which verifies best equation (2). Considering this, the introduction of equation (3) in equation (2) gives 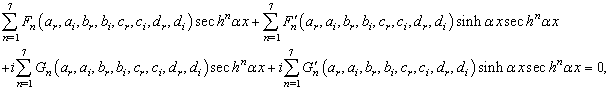
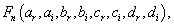
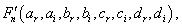
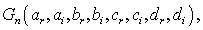 and
and 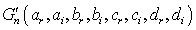 are functions of the coefficients
are functions of the coefficients 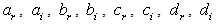 to determine. Equation (4) is called the range equations of coefficients with factors
to determine. Equation (4) is called the range equations of coefficients with factors 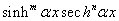 where
where  and
and 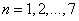 . This equation has a real part and the imaginary part. On identifying the two parts of equation (4) equal to zero, we obtain the following equations classified in order of priority [24,25]. Hence the real part of equation (4) gives
. This equation has a real part and the imaginary part. On identifying the two parts of equation (4) equal to zero, we obtain the following equations classified in order of priority [24,25]. Hence the real part of equation (4) gives 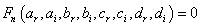 as:Term in
as:Term in 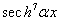 ,
,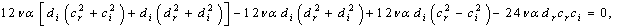
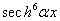 ,
,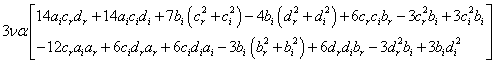
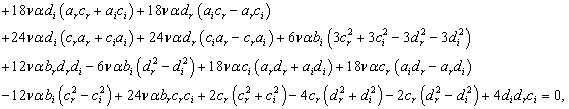
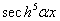 ,
,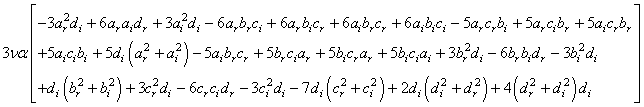
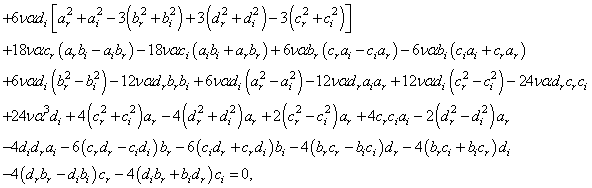
 ,
,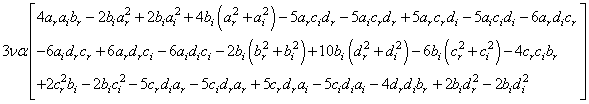
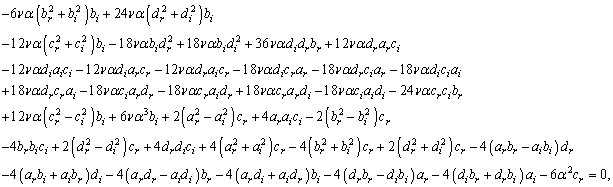
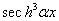 ,
,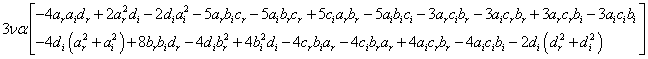
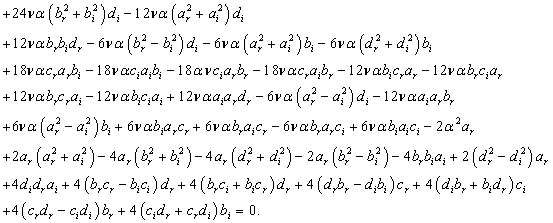
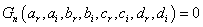 such as:Term in
such as:Term in 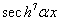 ,
,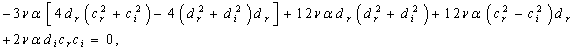
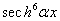 ,
,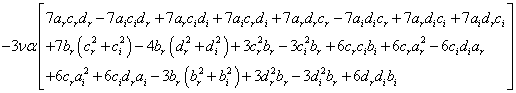
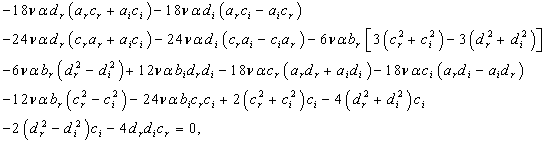
 ,
,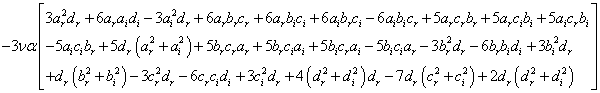
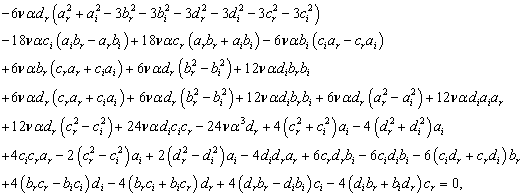
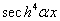 ,
,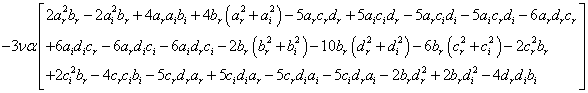
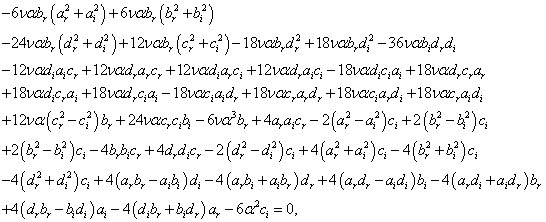
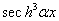 ,
,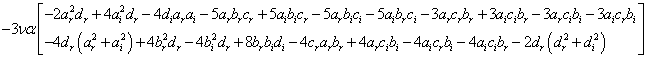
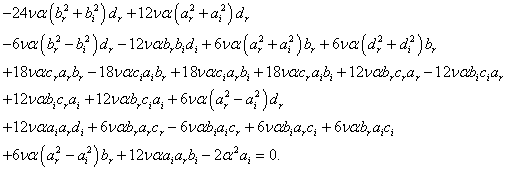
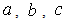 and
and 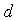 are complex (
are complex (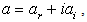
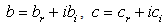 ); this in the goal to multiply the possibilities of obtaining the shape of the most suitable solution. This being, the sets of equations (10), (11), (12), (13) and (14) possess 8 unknowns
); this in the goal to multiply the possibilities of obtaining the shape of the most suitable solution. This being, the sets of equations (10), (11), (12), (13) and (14) possess 8 unknowns 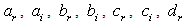 and
and 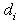 whose resolution is not easy because of their nonlinearity. Of all considered hypotheses, we got two that allowed us to get acceptable solutions.The groups of equations (10), (11), (12), (13) and (14) lead to identities while the groups of equations (5), …, (9) becomeTerm in
whose resolution is not easy because of their nonlinearity. Of all considered hypotheses, we got two that allowed us to get acceptable solutions.The groups of equations (10), (11), (12), (13) and (14) lead to identities while the groups of equations (5), …, (9) becomeTerm in 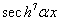 ,
,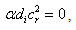
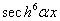 ,
,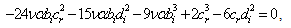
 ,
,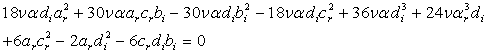
 ,
,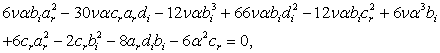
 ,
,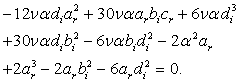
 and
and 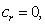 the case where
the case where 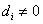 and
and 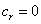 , and the case where
, and the case where 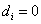 and
and 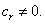 But in the continuation we are going to be interested in the last two quoted cases.First caseWhen
But in the continuation we are going to be interested in the last two quoted cases.First caseWhen 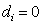 and
and 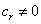 , the equations (16), (17),..., (19) become respectively
, the equations (16), (17),..., (19) become respectively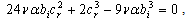
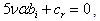
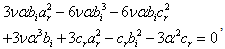
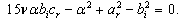
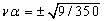 and thereafter, the combination of equations (20), (22) and (23) yields
and thereafter, the combination of equations (20), (22) and (23) yields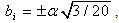
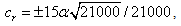
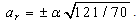
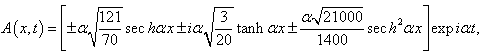
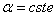 ,
, 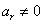 ,
, 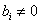 ,
, 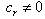 and
and 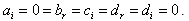 Second case:
Second case: 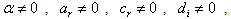
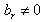 and
and 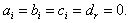 The gotten below equations essentially come from the real part of equation (4) because its imaginary part produced merely identities. Thus, it follows:Term in
The gotten below equations essentially come from the real part of equation (4) because its imaginary part produced merely identities. Thus, it follows:Term in 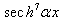 ,
,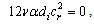
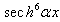 ,
,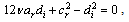
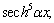
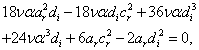
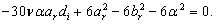
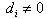 and
and 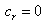 . Hence, the equations (29), (30) and (31) respectively write
. Hence, the equations (29), (30) and (31) respectively write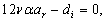
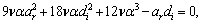
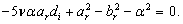
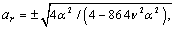
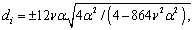
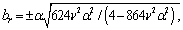
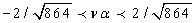 . Substituting equations (35), (36) and (37) in equation (3) we obtain the solution
. Substituting equations (35), (36) and (37) in equation (3) we obtain the solution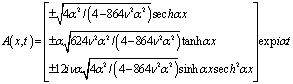
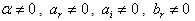 and
and 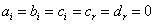 .
. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML