D. G. Yakubu, A. G. Madaki, A. M. Kwami
Mathematical Sciences Programme, Abubakar Tafawa Balewa University, PMB 0248, Bauchi, Nigeria
Correspondence to: D. G. Yakubu, Mathematical Sciences Programme, Abubakar Tafawa Balewa University, PMB 0248, Bauchi, Nigeria.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
We present stable two-step Runge-Kutta collocation methods for solution of highly oscillatory systems of first order initial value problems in ordinary differential equations. These methods are obtained based on multistep collocation at Gaussian points, which are shown to be self-starting, convergent, with large regions of absolute stability. They provide excellent approximations of solutions of oscillatory systems of ordinary differential equations, over the entire interval of integration. This approach has several fascinating advantages, for example, the numerical tests indicate that the methods compare favourably with the standard integrators, both in the quality of the numerical solutions and the computational effort. The results obtained from the preliminary experiments also coincide well with the theoretical values and demonstrate the effectiveness and reliability of this approach.
Keywords:
Block Methods, Continuous Schemes, Matrix Inverse, Runge-Kutta Collocation Methods
Cite this paper: D. G. Yakubu, A. G. Madaki, A. M. Kwami, Stable Two-Step Runge-Kutta Collocation Methods for Oscillatory Systems of Initial Value Problems in ODEs, American Journal of Computational and Applied Mathematics , Vol. 3 No. 2, 2013, pp. 119-130. doi: 10.5923/j.ajcam.20130302.10.
1. Introduction
We present stable two-step Runge-Kutta Collocation (RKC) methods of orders six and eight, with five and seven stages respectively and have large regions of absolute stability. This increased efficiency makes them particularly suitable for solving highly oscillatory large systems of initial value problems in ordinary differential equations (ODEs), of the form,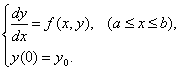 | (1) |
The internal stages of the stable two-step Runge-Kutta collocation methods are the zeros of Legendre polynomials (Gaussian points) which are known to be the best family of implicit Runge-Kutta methods, possessing algebraic stability characteristics with highest order of accuracy for a given number of stages[1]. These Legendre polynomials were chosen because of their superior convergence rate properties and stiffly accurate characteristics in relation to the approximation of functions.Theorem 1.1. Let I denotes the identity matrix of dimension (t+m)×(t+m) and consider the matrices C and D. Then(i) DC = I(ii) 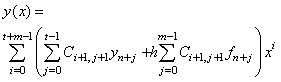 Proof see,[10]
Proof see,[10]
2. Derivation Technique of the Methods
A particularly useful class of discrete method for the solution of (1) is the class of linear multistep method, 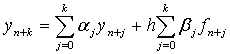 | (2) |
where k>0 is the step number, h is assumed (for simplicity of the analysis) to be a constant step-size given by 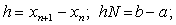
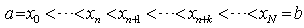 For the construction of the stable two-step Runge-Kutta collocation methods, we consider the following form of a multistep collocation of[10] which was an extension of[9] of the form,
For the construction of the stable two-step Runge-Kutta collocation methods, we consider the following form of a multistep collocation of[10] which was an extension of[9] of the form,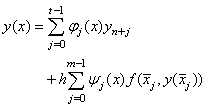 | (3a) |
where t denotes the number of interpolation points 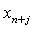 , j = 0,1,2,…,t-1 taken from {xn, xn+k}; and m denotes the distinct collocation points
, j = 0,1,2,…,t-1 taken from {xn, xn+k}; and m denotes the distinct collocation points 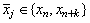 , j = 0,1,2,…,m-1 chosen from {xn, xn+k}. Here y and f are smooth real N-dimensional vector functions and
, j = 0,1,2,…,m-1 chosen from {xn, xn+k}. Here y and f are smooth real N-dimensional vector functions and 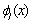 and
and 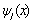 are assumed polynomials of the form,
are assumed polynomials of the form,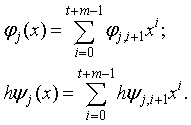 | (3b) |
The numerical constant coefficients 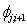 and
and 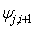 in (3b) are to be determined. They are selected so that accurate approximations of well behaved problems are obtained efficiently. The order of the collocation method (3a) is given by p = t+m-1. The proof of this result follows from[9]. When a collocation point
in (3b) are to be determined. They are selected so that accurate approximations of well behaved problems are obtained efficiently. The order of the collocation method (3a) is given by p = t+m-1. The proof of this result follows from[9]. When a collocation point 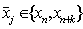 is a Gaussian point then it is counted twice for the order of the method see,[9]. Thus, if all the m collocation points are Gaussian points we have that p = t+2m-1, which gives super-convergence method of[9], also see[11, 12, 15]. The interpolation and collocation conditions are respectively given by,
is a Gaussian point then it is counted twice for the order of the method see,[9]. Thus, if all the m collocation points are Gaussian points we have that p = t+2m-1, which gives super-convergence method of[9], also see[11, 12, 15]. The interpolation and collocation conditions are respectively given by, 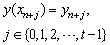 | (4a) |
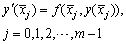 | (4b) |
where 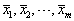 are free collocation points.From the interpolation and collocation conditions (4a)-(4b) and the expression for y(x) in (3a) we see that the following conditions are imposed on
are free collocation points.From the interpolation and collocation conditions (4a)-(4b) and the expression for y(x) in (3a) we see that the following conditions are imposed on 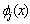 and
and 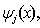
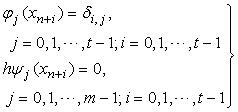 | (5a) |
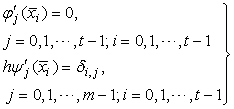 | (5b) |
Writing (5a)-(5b) in a matrix equation of the form in theorem 1.1, we have,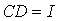 | (6) |
where I is an identity matrix of dimension (t+m)×(t+m), | (7) |
and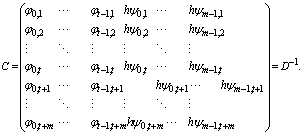 | (8) |
We call D the multistep collocation and interpolation matrix which has a very simple structure and of dimension (t+m)×(t+m). From (6), the columns of C, which give the continuous coefficients, can be obtained from the corresponding columns of D-1. As can be seen the entries of C are the constant coefficients of the polynomial given in (3a) which are to be determined. The matrix C is the solution vector (output) and D is termed the data (input) matrix, which is assumed to be non-singular for the existence of the inverse matrix C. An efficient algorithm for obtaining the elements of the inverse matrix C is found in[10] page 41.Remark 1.1.y(x) given in (3a), is the proposed interpolation and collocation polynomial for (1). From the structure of the matrix D in (7) the inverse matrix exists because the rows are linearly independent as they have distinct values like the Vandermonde matrix. The class of linear multistep method (2) becomes a special class of the multistep collocation method when m = t+1 and 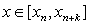 which can also be solve simultaneously to obtain Runge-Kutta collocation method. This interesting connection between the multistep collocation and Runge-Kutta methods is well discussed in[12].Definition 1.1: The method in (3a) has the order of consistency p≥1 provided that there exists an error constant Cp+1 such that the local truncation error (LTE) satisfies
which can also be solve simultaneously to obtain Runge-Kutta collocation method. This interesting connection between the multistep collocation and Runge-Kutta methods is well discussed in[12].Definition 1.1: The method in (3a) has the order of consistency p≥1 provided that there exists an error constant Cp+1 such that the local truncation error (LTE) satisfies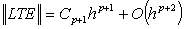 where
where 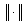 is the maximum norm.
is the maximum norm.
2.1. Stable Two-Step RKC Method of Order Six
In this section we consider some particular method of the stable two-step Runge-Kutta collocation methods, with high accuracy. Using the multistep collocation techniques discussed in section 2 above, we derive single symmetric continuous scheme for accurate solutions of oscillatory systems of initial value problems in ODEs in the interval of integration, based on the zeros of Legendre polynomial. For m = 5, t= 1, we define η = (x-xn), such that the method will be convergent throughout the interval[xn, xn+2], and the matrix D in (7) takes the following form,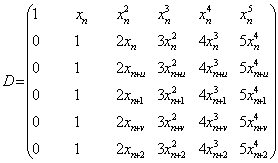 | (9) |
To obtain the values of u and v we find the zeros of P2(x)=0, Legendre polynomial of degree 2 on the standard symmetric interval[-1,1], which in turn were transformed to the interval[xn, xn+2] by means of the following linear transformation 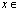 [-1, 1]
[-1, 1] 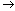 [xn, xn+2],which leads to the following,
[xn, xn+2],which leads to the following,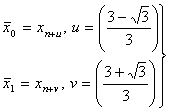 | (10) |
and are valid in the interval[xn, xn+2]. Inverting the matrix D in (9) once, using computer algebra system, for example, Maple software package, leads to the following single symmetric continuous scheme,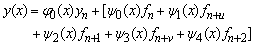 | (11) |
where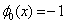 ,
,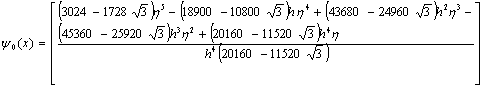
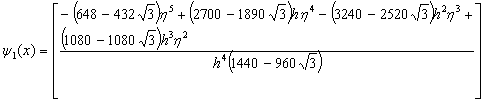 ,
,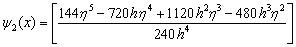 ,
,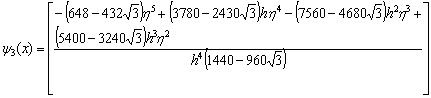
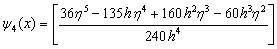 .Evaluating the single symmetric continuous scheme y(x) in (11) at the points, x = xn+2, xn+u, xn+1 and xn+v, we obtain the following block hybrid scheme, which can be solve simultaneously if desired for accurate treatment of highly oscillatory systems of initial value problems in ODEs.
.Evaluating the single symmetric continuous scheme y(x) in (11) at the points, x = xn+2, xn+u, xn+1 and xn+v, we obtain the following block hybrid scheme, which can be solve simultaneously if desired for accurate treatment of highly oscillatory systems of initial value problems in ODEs.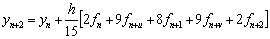
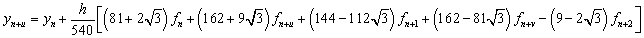
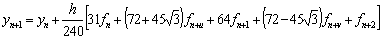
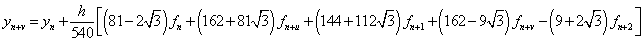 .Converting the block hybrid scheme into stable two-step Runge-Kutta collocation method of order p = 6 written as,
.Converting the block hybrid scheme into stable two-step Runge-Kutta collocation method of order p = 6 written as,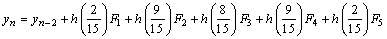 | (12) |
where the stage values at the nth step are calculated as follows,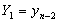
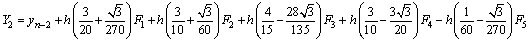
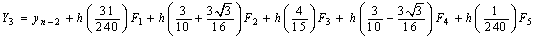
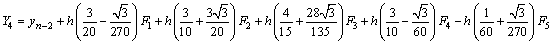
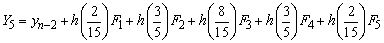 with the stage derivatives
with the stage derivatives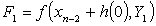
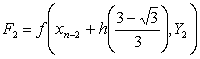
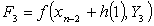
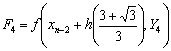
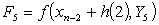 .
.
2.2. Stable Two-Step RKC Method of Order Eight
For the higher order method, we consider a matrix D of the type in (7) as follows,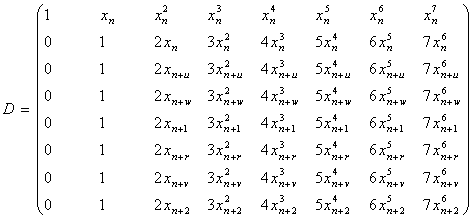 | (13a) |
where u, w and v are zeros of Legendre polynomial of the form P3(x)=0, obtained in the same manner as in equation (10) which are also valid in the interval[xn, xn+2] with,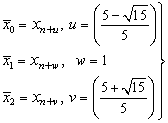 | (13b) |
and r = 3/2. Inverting the matrix D in (13a) once, using computer algebra system, for instance, Maple leads to the following single symmetric continuous scheme,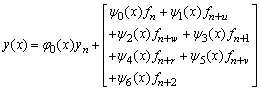 | (14) |
where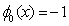 ,
,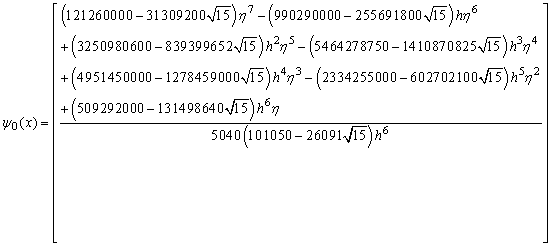
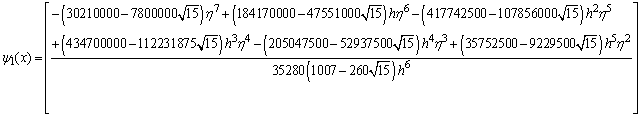 ,
,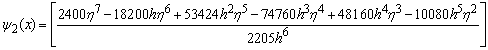
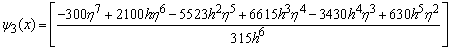 ,
,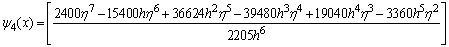
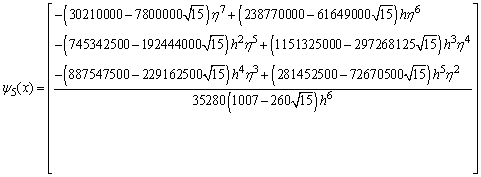 ,
,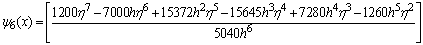 .If we evaluate the single symmetric continuous scheme y(x) in (14) at the points, x = xn+2, xn+u, xn+w, xn+1, xn+r and xn+v, we obtain the following block hybrid scheme,
.If we evaluate the single symmetric continuous scheme y(x) in (14) at the points, x = xn+2, xn+u, xn+w, xn+1, xn+r and xn+v, we obtain the following block hybrid scheme, 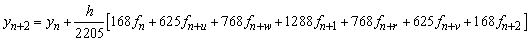
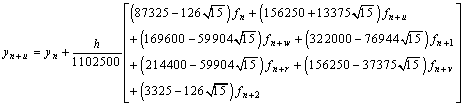
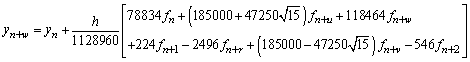
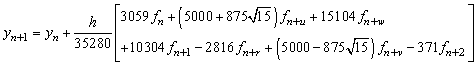
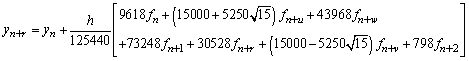 From the block hybrid scheme, we obtain highly stable two-step Runge-Kutta collocation method of order p = 8,
From the block hybrid scheme, we obtain highly stable two-step Runge-Kutta collocation method of order p = 8,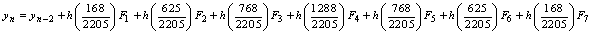 | (15) |
where the stage values at the nth step are calculated as,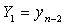
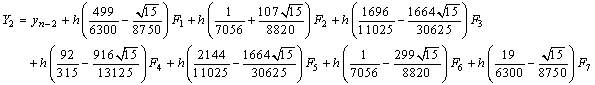
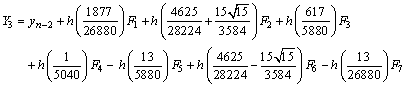
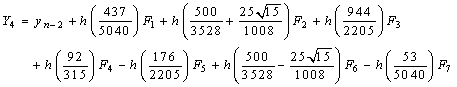
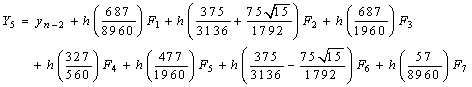
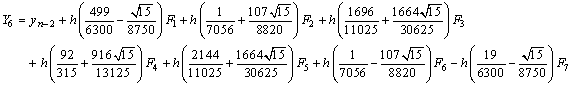
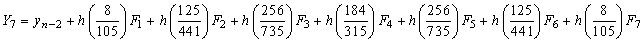 with the stage derivatives
with the stage derivatives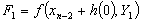
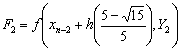
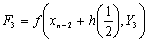
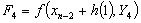
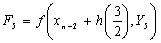
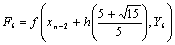
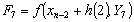 We plotted the regions of absolute stability of methods (12) and (15), using the method used in[5] as shown in figure 1.
We plotted the regions of absolute stability of methods (12) and (15), using the method used in[5] as shown in figure 1.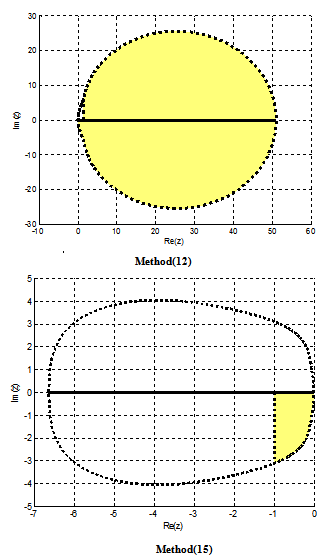 | Figure 1. Regions of absolute stability of the two-step RKC methods |
3. Numerical Examples
For the stable two-step Runge-Kutta collocation methods with large regions of absolute stability, we have evaluated their performance on a set of challenging oscillatory systems of initial value problems which have appeared in the literature and compared the results with the theoretical solutions and with solutions from some methods of similar derivation. The test examples are systems of initial value problems in ordinary differential equations written as first order initial value problems. We plotted these solutions and compared with the exact solutions and we found out that it is difficult to differentiate between the graphs of the computed solutions and graphs of the exact solutions. The number of functions evaluations (nfe) used in each computation is indicated Example 1:In the first example, we consider the famous test problem of Van der Pol’s equation which described the behaviour of oscillator circuits[4]. Originally, the problem had the form of a second order differential equation,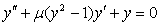 where the parameter μ is set to be either large or small depending on whether the equation is a stiff problem or non-stiff problem. Thus, this can be equivalently written as a coupled system of two first order ordinary differential equation,
where the parameter μ is set to be either large or small depending on whether the equation is a stiff problem or non-stiff problem. Thus, this can be equivalently written as a coupled system of two first order ordinary differential equation,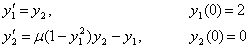 .The graphs of the solutions at the end of the integration interval of[0,100] are plotted and displayed in figure 2.
.The graphs of the solutions at the end of the integration interval of[0,100] are plotted and displayed in figure 2.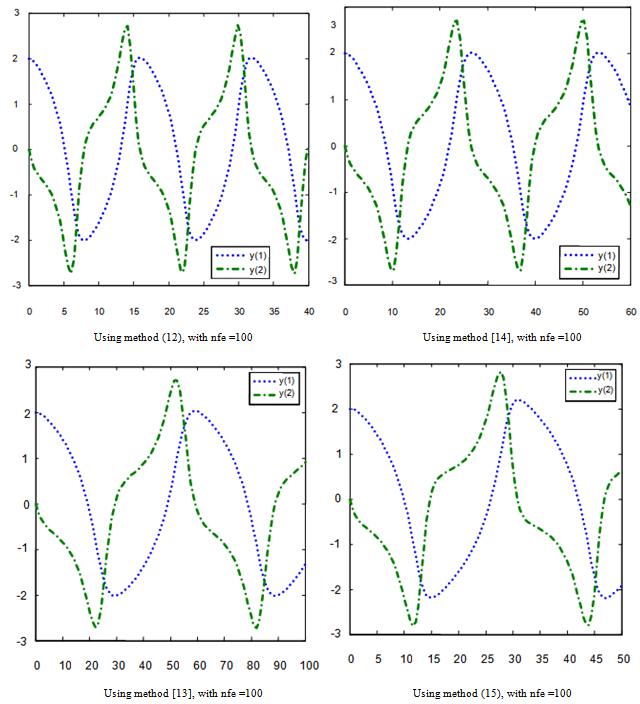 | Figure 2. Graphical solutions of example 1 using RKC methods |
Example 2: The second example is a test problem taken from[8],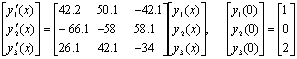 The exact solution is,
The exact solution is,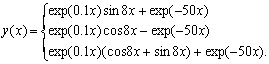 The eigenvalues of the system are λ1=-50 and λ2,3 = 0.1±8i. The graphical plots are displayed in figure 3.Using method (12), with nfe =100 Using method[14], with nfe =100Using method[13], with nfe =100 Using method (15), with nfe =100
The eigenvalues of the system are λ1=-50 and λ2,3 = 0.1±8i. The graphical plots are displayed in figure 3.Using method (12), with nfe =100 Using method[14], with nfe =100Using method[13], with nfe =100 Using method (15), with nfe =100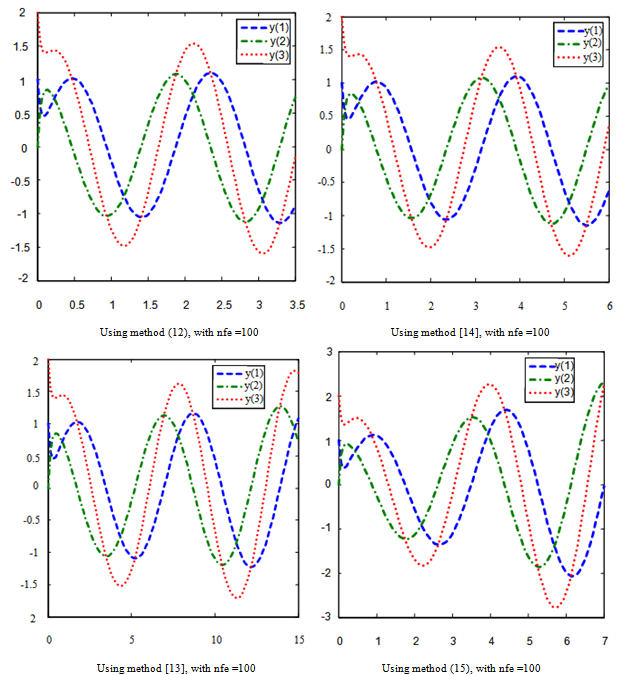 | Figure 3. Graphical solutions of example 2 using RKC Methods |
Example 3: Almost periodic initial value problem.We consider the almost periodic initial value problem which was earlier studied by some eminent authors, for instance[6] and the references therein.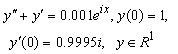 | (16a) |
whose theoretical solution is,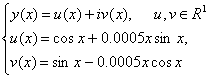 | (16b) |
which represent motion on a perturbation of a circular orbit in the complex plane in which the point y(x) spiral outwards such that its distance from the origin at any time x is given by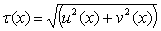 | (16c) |
The initial value problem in (16a) can be expressed as,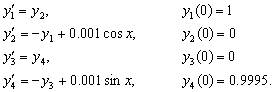 | (16d) |
We solve the system in (16d) and all the solutions generated by the new methods follow the path of the theoretical graphs or exact solutions, see figure 4.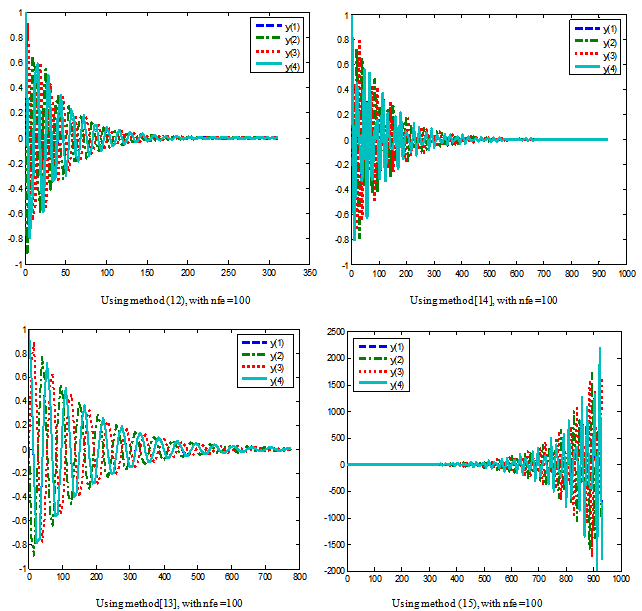 | Figure 4. Graphical solutions of example 3 using RKC Methods |
Example 4: We consider another linear problem which is particularly referred to by[6] as a troublesome problem for some existing methods on which package do exist, for example the DIFSUB of[7]. The eigenvalues of the Jacobian are λ1,2 =-10±100i, λ3 = -4, λ4 = -1, λ5 = -0.5 and λ6 = -0.1. We solve the problem in the range 0≤x≤400. The computed solutions are shown in table 1, while the graphical outputs are displayed in figure 5.
We solve the problem in the range 0≤x≤400. The computed solutions are shown in table 1, while the graphical outputs are displayed in figure 5.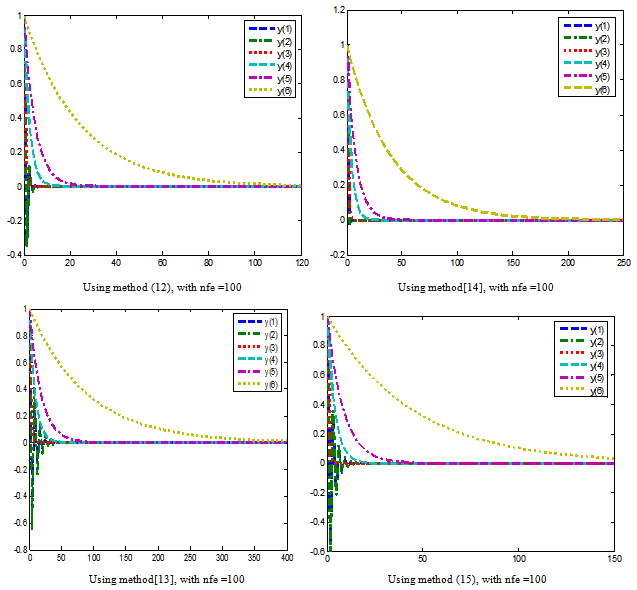 | Figure 5. Graphical solutions of Example 4 using RKC methods |
Table 1. Absolute errors of numerical solutions of example 4
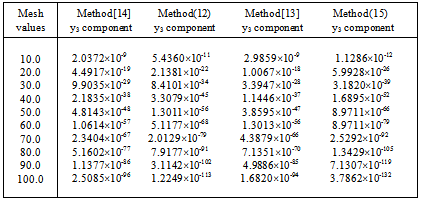 |
| |
|
4. Conclusions
The purpose of this work was to describe the derivation of stable two-step Runge-Kutta collocation methods and their efficient implementation for the numerical integration of highly oscillatory systems of ordinary differential equations. Our aim was to construct highly stable schemes which are computationally more efficient than many of the existing numerical integrators of oscillatory systems. An important factor in favour of the approach developed in this paper is that we have derived stable schemes of orders 6 and 8 with only five and seven stages respectively and it is reasonable to conjecture that it is possible, using the same procedure, to derive still higher order, stable schemes. The numerical results presented are quite satisfactory and suggest that these methods may have a useful role in the solutions of oscillatory systems of initial value problems in ordinary differential equations. Further, each block of the hybrid scheme, was reformulated in form of general linear method[2,3] with the matrices A, U, B and V, which enabled us to plot the stability regions of the methods, using the method used in[5] and are displayed as figure 1 in the paper.
References
| [1] | U. Ascher and G. Bader, Stability of Collocation at Gaussian Points, SIAM, Journal on Numerical Analysis, 23(2) 412 – 422, 1986. |
| [2] | J.C. Butcher, The Numerical Analysis of Ordinary Differential Equations: Runge-Kutta and General Linear Methods, Wiley, Chichester and New York,1987. |
| [3] | J.C. Butcher, Numerical Methods for Ordinary Differential Equations, John Wiley and Sons, Ltd, 2003. |
| [4] | J.C. Butcher, Numerical Methods for Ordinary Differential Equations, Second Edition, John Wiley and Sons, Ltd, 2008. |
| [5] | J. Chollom and Z. Jackiewicz, Construction of two-step Runge-Kutta methods with large regions of absolute stability, Journal of Comput. Appl. Math. 157, 125 – 137, 2003. |
| [6] | S. O. Fatunla, Numerical Integrators for Stiff and Highly Oscillatory Differential Equations, J. Mathematics of Computation, 34 (150) 373 – 390, 1980. |
| [7] | C.W. Gear, “Algorithm 407: DIFSUB for solution of ordinary differential equations,” Comm. ACM, 14, 185 – 190, 1971. |
| [8] | J. D. Lambert, Numerical Methods for Ordinary Differential Systems, John Wiley, New York, 1991. |
| [9] | I. Lie and S. P. Nørsett, Superconvergence for Multistep Collocation, J. Math. of Computation, 52(185) 65 – 79, 1989. |
| [10] | P. Onumanyi, D. O. Awoyemi, S. N. Jator and U. W. Sirisena, New Linear Multistep Methods with Continuous Coefficients for first Order Initial Value Problems, J. of the Nigerian Mathematical Society,(JNMS) 13, 37 – 51, 1994. |
| [11] | U. W. Sirisena, P. Onumanyi and D. G. Yakubu, Towards Uniformly Accurate Continuous Finite DifferenceApproximation of ODEs, B. J. Pure and Applied Sciences, 1, 5-8, 2001. |
| [12] | D. G. Yakubu, Some New Implicit Runge-Kutta Methods from Collocation for Initial Value Problem in Ordinary Differential Equations, Ph.D. Thesis, Abubakar Tafawa Balewa University, Bauchi, Nigeria, 2003. |
| [13] | D. G. Yakubu, Single-Step Implicit Runge-Kutta Method Based on Lobatto Points for Ordinary Differential Equations, J. of the Nigerian Mathematical Society, 22, 57– 70, 2003. |
| [14] | D. G. Yakubu, N. H. Manjak, S. S. Buba and A. I. Maksha, A family of uniformly accurate order Lobatto Runge-Kutta collocation methods, J. Computational and Applied Mathematics, 30(2) 315-330, 2011. |
| [15] | M.Zennaro, One-step Collocation: Uniform Superconergence, Predictor-Corrector Method, Local Error Estimate, SIAM Journal on Numerical Analysis. 22 (6) 1135 – 1152, 1985. |

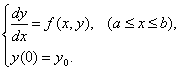
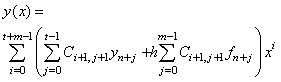 Proof see,[10]
Proof see,[10]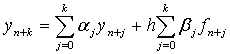
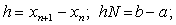
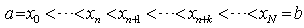 For the construction of the stable two-step Runge-Kutta collocation methods, we consider the following form of a multistep collocation of[10] which was an extension of[9] of the form,
For the construction of the stable two-step Runge-Kutta collocation methods, we consider the following form of a multistep collocation of[10] which was an extension of[9] of the form,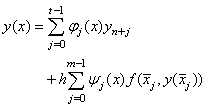
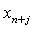 , j = 0,1,2,…,t-1 taken from {xn, xn+k}; and m denotes the distinct collocation points
, j = 0,1,2,…,t-1 taken from {xn, xn+k}; and m denotes the distinct collocation points 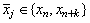 , j = 0,1,2,…,m-1 chosen from {xn, xn+k}. Here y and f are smooth real N-dimensional vector functions and
, j = 0,1,2,…,m-1 chosen from {xn, xn+k}. Here y and f are smooth real N-dimensional vector functions and 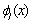 and
and 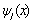 are assumed polynomials of the form,
are assumed polynomials of the form,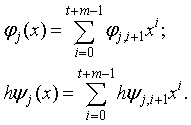
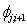 and
and 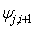 in (3b) are to be determined. They are selected so that accurate approximations of well behaved problems are obtained efficiently. The order of the collocation method (3a) is given by p = t+m-1. The proof of this result follows from[9]. When a collocation point
in (3b) are to be determined. They are selected so that accurate approximations of well behaved problems are obtained efficiently. The order of the collocation method (3a) is given by p = t+m-1. The proof of this result follows from[9]. When a collocation point 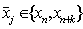 is a Gaussian point then it is counted twice for the order of the method see,[9]. Thus, if all the m collocation points are Gaussian points we have that p = t+2m-1, which gives super-convergence method of[9], also see[11, 12, 15]. The interpolation and collocation conditions are respectively given by,
is a Gaussian point then it is counted twice for the order of the method see,[9]. Thus, if all the m collocation points are Gaussian points we have that p = t+2m-1, which gives super-convergence method of[9], also see[11, 12, 15]. The interpolation and collocation conditions are respectively given by, 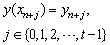
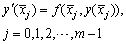
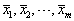 are free collocation points.From the interpolation and collocation conditions (4a)-(4b) and the expression for y(x) in (3a) we see that the following conditions are imposed on
are free collocation points.From the interpolation and collocation conditions (4a)-(4b) and the expression for y(x) in (3a) we see that the following conditions are imposed on 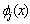 and
and 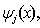
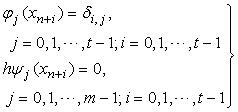
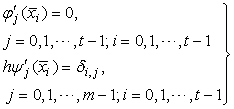
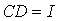

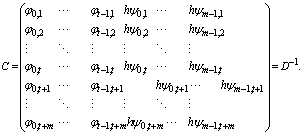
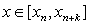 which can also be solve simultaneously to obtain Runge-Kutta collocation method. This interesting connection between the multistep collocation and Runge-Kutta methods is well discussed in[12].Definition 1.1: The method in (3a) has the order of consistency p≥1 provided that there exists an error constant Cp+1 such that the local truncation error (LTE) satisfies
which can also be solve simultaneously to obtain Runge-Kutta collocation method. This interesting connection between the multistep collocation and Runge-Kutta methods is well discussed in[12].Definition 1.1: The method in (3a) has the order of consistency p≥1 provided that there exists an error constant Cp+1 such that the local truncation error (LTE) satisfies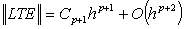 where
where 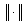 is the maximum norm.
is the maximum norm.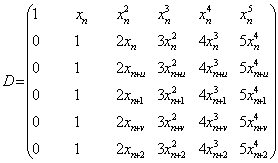
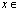 [-1, 1]
[-1, 1]  [xn, xn+2],which leads to the following,
[xn, xn+2],which leads to the following,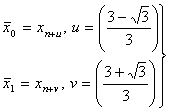
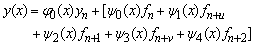
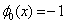 ,
,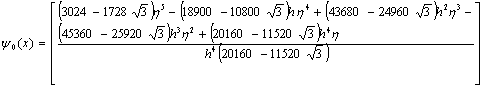
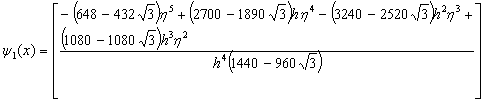 ,
,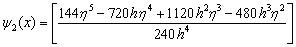 ,
,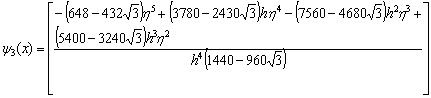
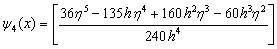 .Evaluating the single symmetric continuous scheme y(x) in (11) at the points, x = xn+2, xn+u, xn+1 and xn+v, we obtain the following block hybrid scheme, which can be solve simultaneously if desired for accurate treatment of highly oscillatory systems of initial value problems in ODEs.
.Evaluating the single symmetric continuous scheme y(x) in (11) at the points, x = xn+2, xn+u, xn+1 and xn+v, we obtain the following block hybrid scheme, which can be solve simultaneously if desired for accurate treatment of highly oscillatory systems of initial value problems in ODEs.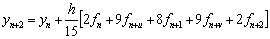
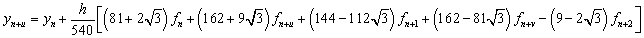
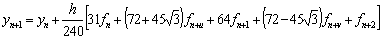
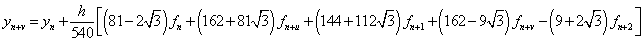 .Converting the block hybrid scheme into stable two-step Runge-Kutta collocation method of order p = 6 written as,
.Converting the block hybrid scheme into stable two-step Runge-Kutta collocation method of order p = 6 written as,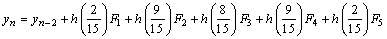
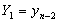
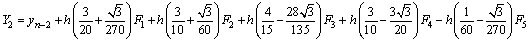
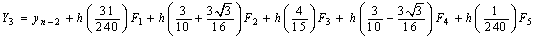
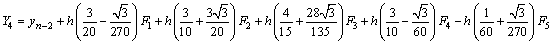
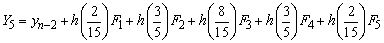 with the stage derivatives
with the stage derivatives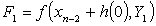
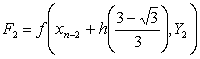
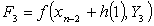
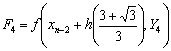
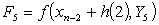 .
.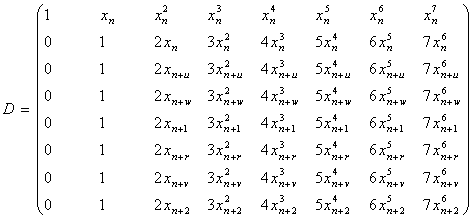
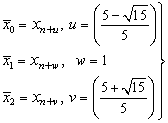
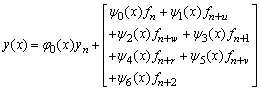
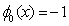 ,
,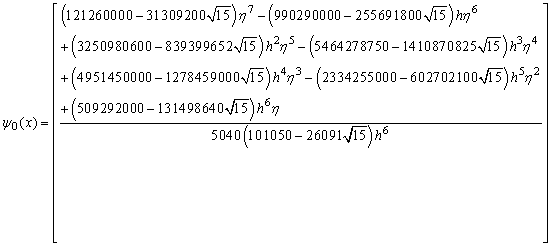
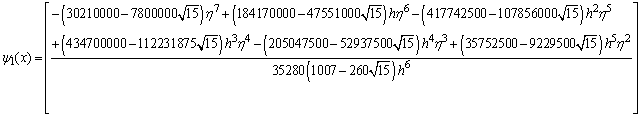 ,
,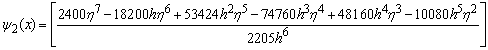
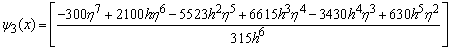 ,
,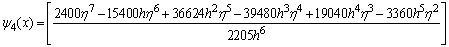
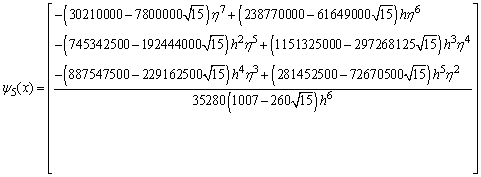 ,
,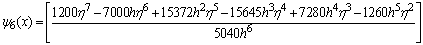 .If we evaluate the single symmetric continuous scheme y(x) in (14) at the points, x = xn+2, xn+u, xn+w, xn+1, xn+r and xn+v, we obtain the following block hybrid scheme,
.If we evaluate the single symmetric continuous scheme y(x) in (14) at the points, x = xn+2, xn+u, xn+w, xn+1, xn+r and xn+v, we obtain the following block hybrid scheme, 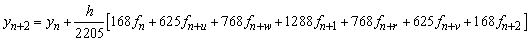
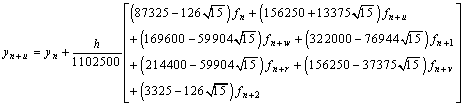
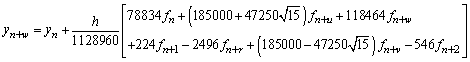
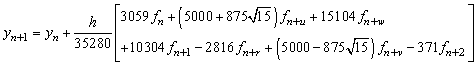
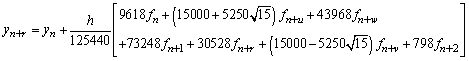 From the block hybrid scheme, we obtain highly stable two-step Runge-Kutta collocation method of order p = 8,
From the block hybrid scheme, we obtain highly stable two-step Runge-Kutta collocation method of order p = 8,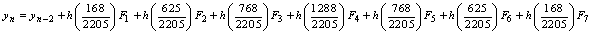
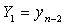
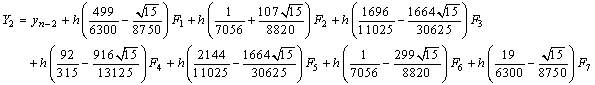
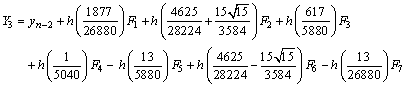
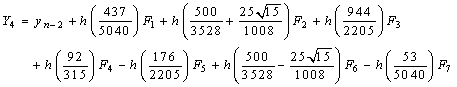
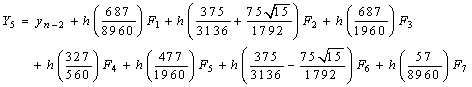
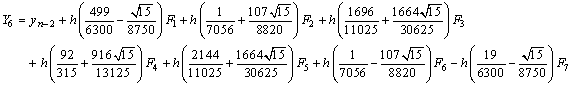
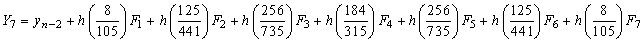 with the stage derivatives
with the stage derivatives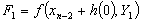
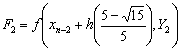
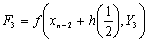
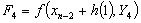
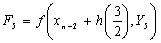
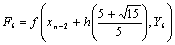
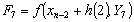 We plotted the regions of absolute stability of methods (12) and (15), using the method used in[5] as shown in figure 1.
We plotted the regions of absolute stability of methods (12) and (15), using the method used in[5] as shown in figure 1.
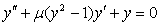 where the parameter μ is set to be either large or small depending on whether the equation is a stiff problem or non-stiff problem. Thus, this can be equivalently written as a coupled system of two first order ordinary differential equation,
where the parameter μ is set to be either large or small depending on whether the equation is a stiff problem or non-stiff problem. Thus, this can be equivalently written as a coupled system of two first order ordinary differential equation,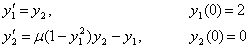 .The graphs of the solutions at the end of the integration interval of[0,100] are plotted and displayed in figure 2.
.The graphs of the solutions at the end of the integration interval of[0,100] are plotted and displayed in figure 2.
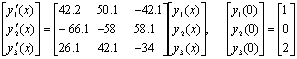 The exact solution is,
The exact solution is,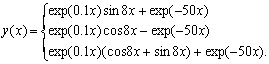 The eigenvalues of the system are λ1=-50 and λ2,3 = 0.1±8i. The graphical plots are displayed in figure 3.Using method (12), with nfe =100 Using method[14], with nfe =100Using method[13], with nfe =100 Using method (15), with nfe =100
The eigenvalues of the system are λ1=-50 and λ2,3 = 0.1±8i. The graphical plots are displayed in figure 3.Using method (12), with nfe =100 Using method[14], with nfe =100Using method[13], with nfe =100 Using method (15), with nfe =100
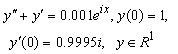
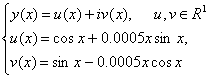
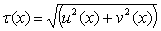
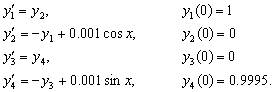

 We solve the problem in the range 0≤x≤400. The computed solutions are shown in table 1, while the graphical outputs are displayed in figure 5.
We solve the problem in the range 0≤x≤400. The computed solutions are shown in table 1, while the graphical outputs are displayed in figure 5.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML