Rajesh C. Shah1, Rajiv B. Shah2
1Department of Applied Mathematics, Faculty of Technology and Engineering, The M. S. University of Baroda, Vadodara, 390 001, Gujarat State, India
2Department of Applied Mathematics, Polytechnic, The M. S. University of Baroda, Vadodara, 390 002, Gujarat State, India
Correspondence to: Rajesh C. Shah, Department of Applied Mathematics, Faculty of Technology and Engineering, The M. S. University of Baroda, Vadodara, 390 001, Gujarat State, India.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
The aim of the present paper is to propose new iterative schemes for finding a root of a nonlinear algebraic equation f (x) = 0 for a given initial guess value x0. The iterative schemes can be obtained using Taylor’s series expansion for f (x0 ± h). From the convergence analysis, the various orders of convergence are obtained like linear, order 2 and order 3/2. Some examples are also discussed and compared with Newton’s method. Some iterative scheme also works even if f '(x)=0, which is the limitation of the Newton’s method.
Keywords:
Iterative Method, Ordinate – Abscissa Method, Algebraic Equations
Cite this paper: Rajesh C. Shah, Rajiv B. Shah, New Ordinate-Abscissa Based Iterative Schemes to Solve Nonlinear Algebraic Equations, American Journal of Computational and Applied Mathematics , Vol. 3 No. 2, 2013, pp. 112-118. doi: 10.5923/j.ajcam.20130302.09.
1. Introduction
Finding a root of an algebraic equation is always curiosity for many researcher in their science and engineering problems. Among the various techniques, Newton’s method [1–4] is the most popular and having quadratic convergence. Many researchers[5–15] have tried to develop new iterative scheme in their analysis for faster convergence and claim their advantage over Newton’s method. In this paper, various new iterative schemes (Ordinate – Abscissa based Schemes) are proposed. The various possibility of convergences like linear convergence, convergence of order 3/2, and convergence of order 2 are obtained.Moreover, some proposed scheme also works even if 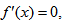 which is the limitation of the Newton’s method.
which is the limitation of the Newton’s method.
2. The Basic Idea of Various New Iterative Schemes
The geometrical view of the method is as shown in figure 1.Consider the following nonlinear algebraic equation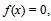 | (1) |
for which one or more real roots to be found.Considering x0 as an initial guess value and x* as exact root, then from the figure 1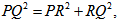 which implies
which implies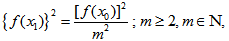 | (2) |
where m indicates number of divisions of ordinate ( in our case f(x0)).Case I When x > x*Let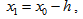 | (3) |
be the first approximation to the required root of equation (1).Then equation (2) becomes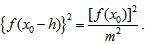 | (4) |
(A) Using Taylor’s series expansion and neglecting terms containing 0 (h2) and higher as 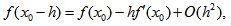 | (5) |
equation (4) becomes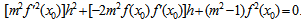 | (6) |
Considering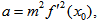
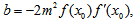
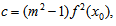 equation (6) becomes
equation (6) becomes 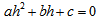 which on solving for h gives
which on solving for h gives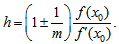 | (7) |
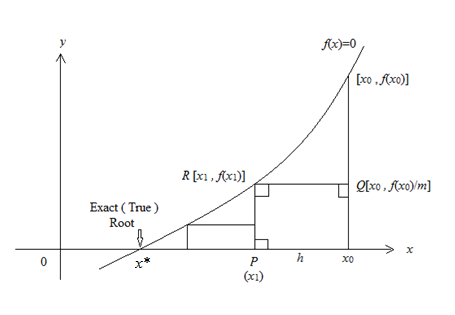 | Figure 1. Ordinate - Abscissa method |
Therefore, from equation (3) the first approximation can be obtained as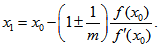 | (8) |
The general formula for successive approximation is, therefore, given by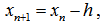 | (9) |
which implies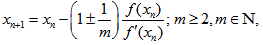 | (10) |
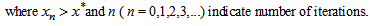 (B) Using Taylor’s series expansion and neglecting terms containing 0 (h3) and higher as
(B) Using Taylor’s series expansion and neglecting terms containing 0 (h3) and higher as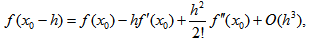 | (11) |
equation (4) becomes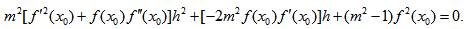 | (12) |
Considering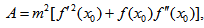
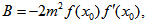
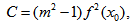 equation (12) becomes
equation (12) becomes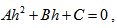 | (13) |
which on solving for h gives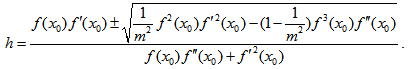 | (14) |
Therefore, from equation (3) the first approximation can be obtained as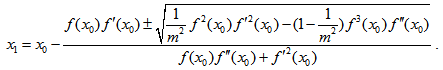 | (15) |
The general formula for successive approximation is , therefore, given by 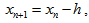 | (16) |
which implies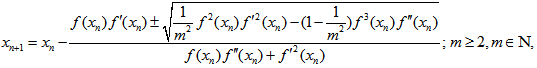 | (17) |
where 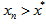 .Case II When x0 < x*In this case
.Case II When x0 < x*In this case 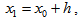 | (18) |
be the first approximation to the required root of equation (1). Then equation (2) becomes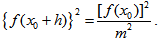 | (19) |
(A)By following the same procedure as in Case I (A) , the general formula for successive approximation can be obtained as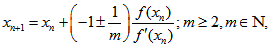 | (20) |
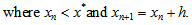 (B) By following the same procedure as in Case I (B), the general formula for successive approximation can be obtained as
(B) By following the same procedure as in Case I (B), the general formula for successive approximation can be obtained as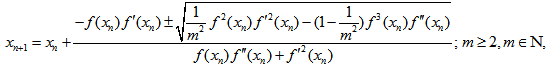 | (21) |
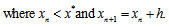 Combining formulae (10) and (20) yields the iterative scheme
Combining formulae (10) and (20) yields the iterative scheme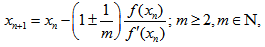 | (22) |
which is true for any initial guess x0 ; that is, whether 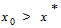 or
or 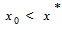 .Scheme (22) implies two different formulas as
.Scheme (22) implies two different formulas as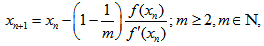 | (23) |
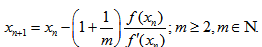 | (24) |
Similarly, combining formulae (17) and (21) yields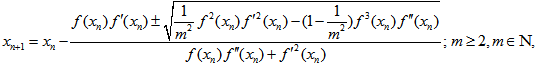 | (25) |
which is true for any initial guess x0.
3. Convergence Analysis
Let 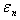 be the error in the nth iteration then
be the error in the nth iteration then 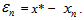 | (26) |
Similarly, let 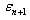 be the error in the ( n + 1 )th iteration then
be the error in the ( n + 1 )th iteration then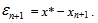 | (27) |
Convergence analysis of scheme (22)Substituting equations (26), (27) in (22) yields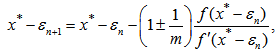 | (28) |
which implies 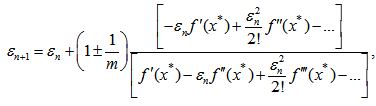 | (29) |
since f(x*)=0.On simplification of equation (29) , one obtains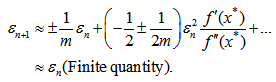 | (30) |
Thus, the scheme (22) converges linearly. However, it can be observed that when m is large then the order of convergence is 2 (Quadratically) and the scheme resemblance to Newton’s formula.Convergence analysis of scheme (25)Substituting equations (26), (27) in (25), the separate simplifications of each term in (25) gives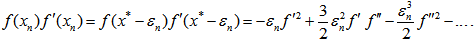 | (31) |
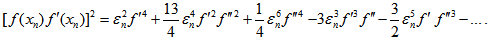 | (32) |
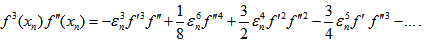 | (33) |
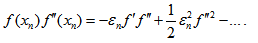 | (34) |
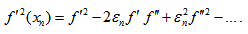 | (35) |
The term under square root sign in (25) is given by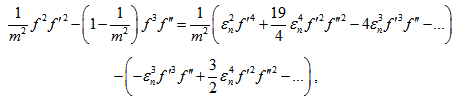 | (36) |
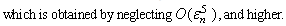 The denominator term in (25) is given by
The denominator term in (25) is given by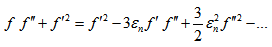 | (37) |
The second term in (25) is given by 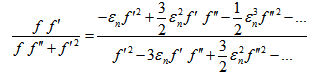 | (38) |
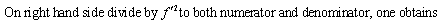
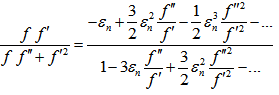 | (39) |
The third term in (25) is given by 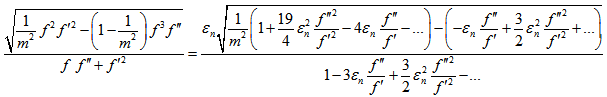 | (40) |
Using equations (26),(27) in (25) , and using equations (31)-(40), one obtains on simplification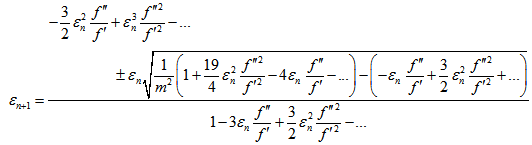 | (41) |
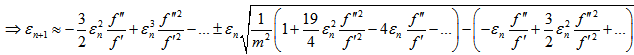 | (42) |
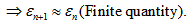 | (43) |
Thus, the scheme (25) converges linearly. However, it can be observed from equation (42) that when m is large then the order of convergence is 3/2.
4. Discussion of some Examples
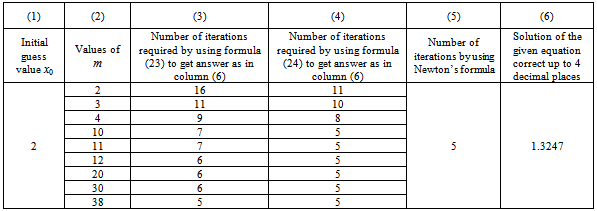
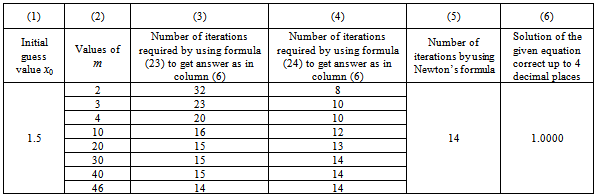
As the proposed iterative scheme (22) converges quadratically when m is large, so a comparison of this scheme with Newton’s method is given. It is observed from Table 1 that by using Newton’s method, the answer correct up to four decimal places is 1.3247 which is obtained in 5 iterations whereas using our method the same answer is obtained when(1) m = 38 for formula (23) ( Column 3 ) ; that is , the number of iterations remains 5 as in Newton’s case.(2) m = 10 for formula (24) (column 4 ); that is , the number of iterations remains 5 as in Newton’s case.It is observed from Table 2 that by using Newton’s method, the answer correct up to four decimal places is 1.0000 which is obtained in 14 iterations whereas using our method the same answer is obtained when(1) m = 46 for formula (23) (column 3) ; that is , the number of iterations remains 14 as in Newton’s case.(2) m = 2 for formula (24) (column 4) ; that is , the number of iterations required are 8 which are less than Newton’s case where it requires 14. So, faster convergence is obtained.By observing both the examples carefully, it is concluded that the new proposed iterative scheme is comparable with Newton’s scheme. Moreover, for example in Table 2, faster convergence is obtained for the formula (24) in column 4.Table 1. Comparative study of our scheme (22) with Newton’s formula for x3x1=0
 |
| |
|
Table 2. Comparative study of our scheme (22) with Newton’s formula for x3x2x+1=0
 |
| |
|
5. Conclusions
The present paper proposes new iterative schemes for finding a root of a nonlinear algebraic equation f (x) = 0. The discussion Section 4 shows the comparison of our method with Newton’s Method. The following are the major conclusions obtained:(1) The scheme (22) converges linearly. However, when m is large, the order of convergence is 2 and the scheme resemblance to Newton’s formula. (2) The necessary condition for convergence of the scheme (25) is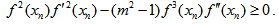 Also, the condition of validity of the scheme is
Also, the condition of validity of the scheme is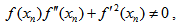 which implies
which implies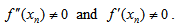 (3) The scheme in (25) works even if
(3) The scheme in (25) works even if 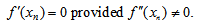 (4) The scheme (25) has linear convergence. However, when m is large the order of convergence is 3/2. (5) There is no restriction on initial guess
(4) The scheme (25) has linear convergence. However, when m is large the order of convergence is 3/2. (5) There is no restriction on initial guess 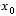 .(6) The beauty of the present schemes (22) and (25) are of choosing value of m, which is in our control.(7) The example discussed in Table 2 shows the faster convergence by our scheme than Newton’s method.
.(6) The beauty of the present schemes (22) and (25) are of choosing value of m, which is in our control.(7) The example discussed in Table 2 shows the faster convergence by our scheme than Newton’s method.
References
| [1] | J. Mathews, Numerical Methods for Mathematics, Science and Engineering, Prentice-Hall, 1987. |
| [2] | M. K Jain, S. R. K. Iyengar, R. K. Jain, Numerical methods – problems and solutions, New Age International Limited, New Delhi, 1994. |
| [3] | E. Suli, D. Mayers, An Introduction to Numerical Analysis, Cambridge University Press, New York, 2003. |
| [4] | R. C. Shah, Intorduction to Complex Variables & Numerical Methods , Books India Publications, Ahmedabad, India 2012. |
| [5] | J. H. He, Newton-Like Iteration Method for Solving Algebraic Equations, Communications in Nonlinear Science & Numerical Simulation 3 (1998) 106-109. |
| [6] | J. H. He, A new iteration method for solving algebraic equations, Applied Mathematics and Computation 135 (2003) 81-84. |
| [7] | V. Kanwar, S. Singh, J. R. Sharma, Mamta, New numerical techniques for solving non-linear equations, Indian Journal of Pure & Applied Mathematics 34(9) (2003) 1339-1349. |
| [8] | E. Galligani, The Newton-arithmetic mean method for the solution of systems of nonlinear equations, Applied Mathematics and Computation 134 (2003) 9–34. |
| [9] | X. G. Luo, A note on the new iteration method for solving algebraic equations, Applied Mathematics and Computation 171 (2005) 1177-1183. |
| [10] | T. Fang, F. Guo, C. Fon, F. Lee, A new iteration method with cubic convergence to solve nonlinear algebraic equations, Applied Mathematics and Computation 175 (2006) 1147-1155. |
| [11] | L. Petkovic´ , M. Petkovic, A note on some recent methods for solving nonlinear equations, Applied Mathematics and Computation 185 (2007) 368–374. |
| [12] | N. Ide, A new hybrid iteration method for solving algebraic equations, Applied Mathematics and Computation 195 (2008) 772–774. |
| [13] | R. Saeed, K. Aziz, An iterative method with quartic convergence for solving nonlinear equations, Applied Mathematics and Computation 202 (2008) 435–440. |
| [14] | A. Maheshwari, A fourth order iterative method for solving nonlinear equations, Applied Mathematics and Computation 211 (2009) 383–391. |
| [15] | R. Barrio , M. Rodríguez, A. Abad, F. Blesa , Breaking the limits: The Taylor series method, Applied Mathematics and Computation 217 (2011) 7940–7954. |

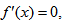 which is the limitation of the Newton’s method.
which is the limitation of the Newton’s method.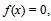
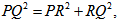 which implies
which implies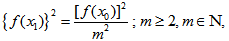
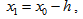
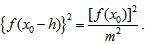
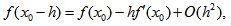
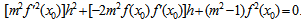
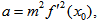
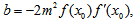
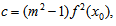 equation (6) becomes
equation (6) becomes 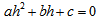 which on solving for h gives
which on solving for h gives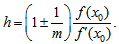

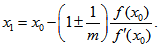
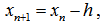
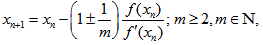
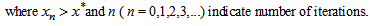 (B) Using Taylor’s series expansion and neglecting terms containing 0 (h3) and higher as
(B) Using Taylor’s series expansion and neglecting terms containing 0 (h3) and higher as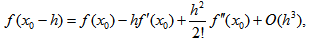
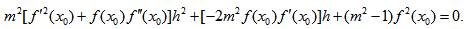
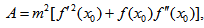
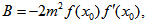
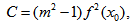 equation (12) becomes
equation (12) becomes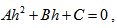
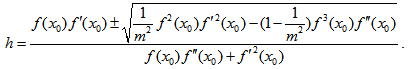
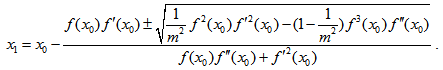
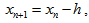
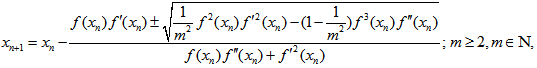
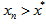 .Case II When x0 < x*In this case
.Case II When x0 < x*In this case 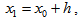
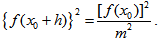
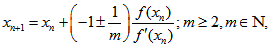
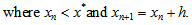 (B) By following the same procedure as in Case I (B), the general formula for successive approximation can be obtained as
(B) By following the same procedure as in Case I (B), the general formula for successive approximation can be obtained as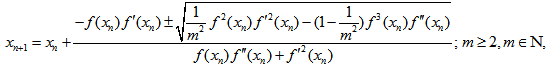
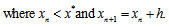 Combining formulae (10) and (20) yields the iterative scheme
Combining formulae (10) and (20) yields the iterative scheme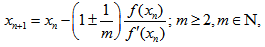
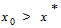 or
or 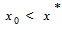 .Scheme (22) implies two different formulas as
.Scheme (22) implies two different formulas as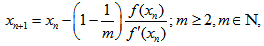
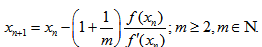
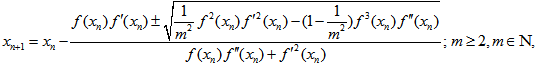
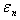 be the error in the nth iteration then
be the error in the nth iteration then 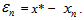
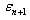 be the error in the ( n + 1 )th iteration then
be the error in the ( n + 1 )th iteration then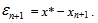
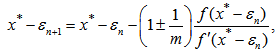
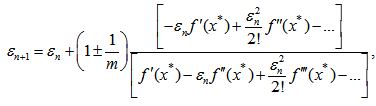
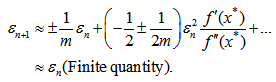
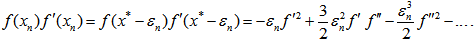
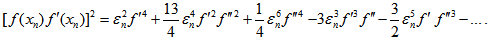
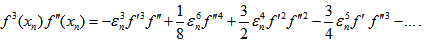
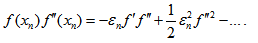
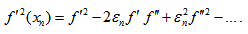
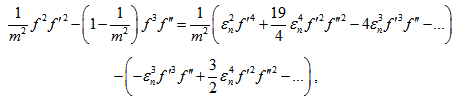
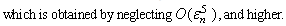 The denominator term in (25) is given by
The denominator term in (25) is given by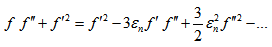
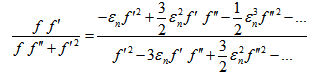
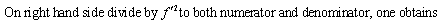
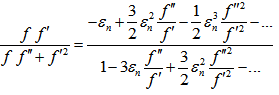
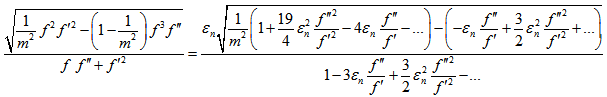
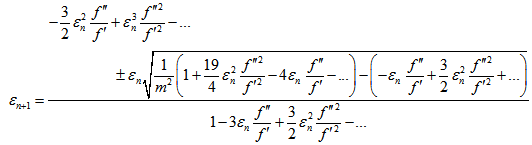
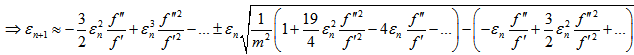
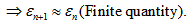
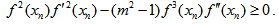 Also, the condition of validity of the scheme is
Also, the condition of validity of the scheme is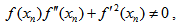 which implies
which implies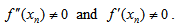 (3) The scheme in (25) works even if
(3) The scheme in (25) works even if 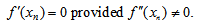 (4) The scheme (25) has linear convergence. However, when m is large the order of convergence is 3/2. (5) There is no restriction on initial guess
(4) The scheme (25) has linear convergence. However, when m is large the order of convergence is 3/2. (5) There is no restriction on initial guess 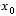 .(6) The beauty of the present schemes (22) and (25) are of choosing value of m, which is in our control.(7) The example discussed in Table 2 shows the faster convergence by our scheme than Newton’s method.
.(6) The beauty of the present schemes (22) and (25) are of choosing value of m, which is in our control.(7) The example discussed in Table 2 shows the faster convergence by our scheme than Newton’s method. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML
