Arun Kumar Gupta, Mamta
Department of Mathematics, M.S. College, Saharanpur, 247001, UP, India
Correspondence to: Arun Kumar Gupta, Department of Mathematics, M.S. College, Saharanpur, 247001, UP, India.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
An analysis and numerical results are presented for free transverse vibrations of rectangular plates of non-linear thickness variation and harmonically temperature distribution on the basis of classical plate theory. Following Levy approach i.e. the two parallel edges are simply supported, the fourth-order differential equation governing the motion of such plates of non-linear varying thickness in one direction with harmonic temperature distribution, has been solved by using the quintic splines interpolation technique for two different combinations of clamped and simply supported boundary conditions at the other two edges. An algorithm for computing the solution of this differential equation is presented, for the case of equal intervals. Effect of the taper constants and thermal constant together with other plate parameters such as aspect ratio on the natural frequencies of vibration is illustrated for the first three modes of vibration.
Keywords:
Non-Linear, Thickness Variation, Harmonic Temperature, Vibration, Rectangular Plate
Cite this paper: Arun Kumar Gupta, Mamta, Non-linear Thickness Variation on Harmonically Thermal Induced Vibration of a Rectangular Plate, American Journal of Computational and Applied Mathematics , Vol. 3 No. 2, 2013, pp. 106-111. doi: 10.5923/j.ajcam.20130302.08.
1. Introduction
In the recent past, there was a phenomenal increase in the development of elastic materials due to the desirability of lightweight, high strength, corrosion resistance and high-temperature performance requirements in modern technology. Plates of composite materials are widely used in many engineering structures and machines. In this era of science and technology plates of various shapes and of variable thickness may be regarded as a first approximation to wings and blades and occur as panels in many forms of engineering structures. Thus knowledge of their natural frequencies is of considerable importance at the design stage in order to avoid resonance excited by internal or external forces. Thus, their design requires an accurate determination of their natural frequencies and mode shapes. An extensive review of the work up to 1985 on linear vibration of isotropic/anisotropic plates of various geometries has been given by Leissa in his monograph [1]. The studies on vibration of rectangular plates with uniform/non-uniform thickness with various edge conditions after 1985 has been carried out by a number of researchers and are reported in refs.[2-5]. Jain and Soni [6] find out the free vibrations of rectangular plates of parabolically varying thickness. Tomar et al.[7] studied the free vibrations of an isotropic non-homogeneous infinite plate of parabolically varying thickness. Singh and Jain[8] have studied the free asymmetric transverse vibration of parabolically varying thickness of polar orthotropic annular plate with flexible edge conditions. Kumar and Tomar[9] studied the free transverse vibrations of monoclinic rectangular plates with continuously varying thickness and density. Gupta et al.[10] studied the vibration analysis of non-homogeneous circular plate of nonlinear thickness variation by differential quadrature method. Gupta et al.[11] have studied the thermal effect on vibration of non-homogeneous orthotropic rectangular plate having bi-directional parabolically varying thickness. Feng and Min[12] have studied the vibrations of axially moving visco-elastic plate with parabolically varying thickness. Gupta et al.[13] studied the vibration of visco-elastic parallelogram plate with parabolic thickness variation. Bhatnagar and Gupta[14] did the vibration analysis of visco-elastic circular plate subjected to thermal gradient. Gupta and Sharma[15] studied the effect of thermal gradient on vibration of trapezoidal plate of linearly varying thickness. Gupta and Singhal[16] studied the effect of non-homogeneity on thermally induced vibration of orthotropic visco-elastic rectangular plate of linearly varying thickness. Tomar and Gupta[17] studied the effect of thermal gradient on frequencies of an orthotropic rectangular plate whose thickness varies in two directions. Gupta and Khanna[18] solved the problem of visco-elastic rectangular plate with linearly thickness variations in both directions. Gupta and Sharma[19] studied the thermally induced vibration of orthotropic trapezoidal plate of linearly varying thickness. Gupta and Sharma[20] discussed the effect of linear thermal gradient on vibration of trapezoidal plates whose thickness varies parabolically. Recently, Gupta and Sharma[21] study the thermally induced vibration of non-homogeneous trapezoidal plate with varying thickness and density.In an up-to-date survey of literature, the authors have not come across any study dealing with vibration of non-linear rectangular plates with the exception of Gupta et al.[10], which deals non-homogeneous circular plate of non-linear thickness variation. Keeping this in view, a study dealing with transverse vibrations of rectangular plates of non-linear (combination of linear and quadratic variation) varying thickness along one direction and harmonic temperature distribution is presented employing classical plate theory. The governing differential equation for such plates with two opposite edges simply supported reduces to fourth-order differential equation with variable coefficients whose analytical solution is not feasible. Quintic splines interpolation technique has been employed to obtain the natural frequencies for two different combinations of clamped and simply supported boundary conditions at the other two edges. This method is preferred because a chain of lower-order approximations may yield a better accuracy than a global higher-order approximation[21] and natural boundary conditions can be considered easily. The effect of various plate parameters has been studied on the natural frequencies for the first three modes of vibration. The consideration of non-linearity thickness variation, harmonic temperature distribution and aspect ratio leads to a very complex problem involving several parameters. However, with the choice of Levy approach and one-dimensional variations in thickness and temperature distribution, one can find the approximate solution of the present problem. This type of variation in thickness and temperature distribution consideration is of interest since it provides reasonable approximation to variation. Thus, the present study of theoretically investigated vibrational characteristics will be of interest to design engineers.
2. Analysis and Equation of Motion
It is assumed that the rectangular plate is subjected to a harmonic temperature distribution along the length i.e. in x-directions[23]: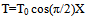 | (1) |
where T denotes the temperature excess above the reference temperature at any point at distance 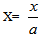 and T0 denotes the temperature excess above reference temperature at the end i.e. x=a or X=1.The temperature dependence of the modulus of elasticity for most of engineering materials is given by[24]:
and T0 denotes the temperature excess above reference temperature at the end i.e. x=a or X=1.The temperature dependence of the modulus of elasticity for most of engineering materials is given by[24]: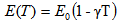 | (2) |
where E0 is the value of the Young's modulus at reference temperature i.e. T=0 and 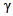 is the slope of the variation of E with T. Taking as the reference temperature, the temperature at the end of plate i.e. at X=1, the modulus variation in view of (1) and (2), becomes
is the slope of the variation of E with T. Taking as the reference temperature, the temperature at the end of plate i.e. at X=1, the modulus variation in view of (1) and (2), becomes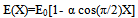 | (3) |
where 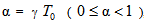 , a constant known as temperature constant.The differential equation governing the free transverse motion of an elastic rectangular plate of length a, breadth b, thickness h and density ρ is
, a constant known as temperature constant.The differential equation governing the free transverse motion of an elastic rectangular plate of length a, breadth b, thickness h and density ρ is 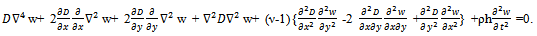 | (4) |
where w is transverse displacement.Let us assume that the two opposite edges y=0 and y=b are simply supported and that thickness varies in x-direction only. Therefore, the thickness h and flexural rigidity D of the plate become a function of x only. For harmonic vibration, w may have Levy type solution as 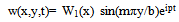 | (5) |
where p is the circular frequency and m is a positive integer.Substitution of equation (5) in (4) gives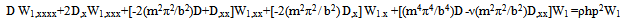 | (6) |
A comma followed by a suffix denotes partial differentiation with respect to that variable.Thus equation (6) reduces to a form independent of y and on introducing the non-dimensional variables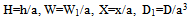 | (7) |
the differential equation (6) reduces to 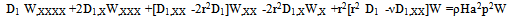 | (8) |
where r2 =(mπa/b)2 .Since thickness varies non-linearly in x-direction only, therefore, one can assume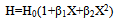 | (9) |
where β1 and β2 are taper constants such that |β1|≤1 , |β2|≤1 and β1+β2>-1, H0 is thickness at X=0.Considering equation (3) and (9) with help of (7), the expression for rigidities D1 comes out as 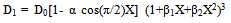 | (10) |
where D0 = E0H03/12(1-ν2) Using equations (8) to (10), one obtains the equation of motion as: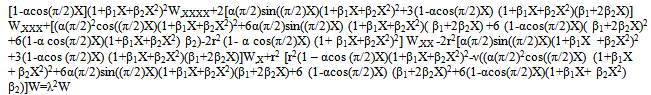 | (11) |
where 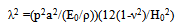 | (12) |
is a frequency parameter.
3. Method of Solution
Let f(X) be a function with continuous derivatives in the range (0,l). Choose (n + 1) points X0, X1, X2, . .., Xn ,in the range O≤X≤l such that 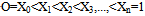 .Let the approximating function W(X) for f(X) be a quintic spline with the following properties :(a) W(X) is a quintic polynomial in each interval (Xk, Xk+1),(b) W(Xk) =f(Xk), k = 0 (1) n,(c) W’(X), W”(X), W’’’(X) and Wiv(X) are continuous.From the definition, a quintic spline takes the form
.Let the approximating function W(X) for f(X) be a quintic spline with the following properties :(a) W(X) is a quintic polynomial in each interval (Xk, Xk+1),(b) W(Xk) =f(Xk), k = 0 (1) n,(c) W’(X), W”(X), W’’’(X) and Wiv(X) are continuous.From the definition, a quintic spline takes the form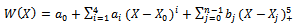 | (13) |
where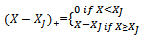 | (14) |
It is also assumed, for simplicity, that the knots Xi are equally spaced in (0,l) with the spacing interval ΔX, so that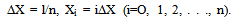 | (15) |
The number of unknown constants in equation (13) is (n + 5). Satisfaction of differential equation (11) by collocation at the (n + 1) knots in the interval (0,l) together with the boundary conditions (to be explained in the next section) gives precisely the requisite number of equations for the determination of unknown constants.Substituting W(X) from equation (13) into equation (11) gives, for satisfaction at the mth knot, one obtains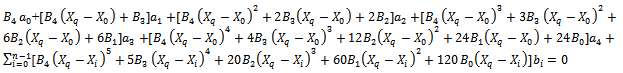 | (16) |
where B0=[1- α cos(π/2)Xq] (1+β1Xq+β2Xq2)2,B1=2[α(π/2)sin((π/2)Xq)(1+β1Xq+β2Xq2)2+3(1-αcos(π/2)Xq) (1+β1Xq+β2Xq2)(β1+2β2Xq)],B2=[(α(π/2)2cos((π/2)Xq)(1+β1Xq+β2Xq2)2+6α(π/2)sin((π/2)Xq) (1+β1Xq+β2Xq2)(β1+2β2Xq)+6 (1-αcos(π/2)Xq) (β1+ 2β2Xq)2 + 6(1-α cos(π/2)Xq)(1+β1Xq+β2Xq2) β2)-2r2 (1-α cos(π/2)Xq) (1+β1Xq+β2Xq2)2],B3 =-2r2[α(π/2)sin((π/2)Xq)(1+β1Xq+β2Xq2)2+3(1-αcos (π / 2)Xq) (1+β1Xq+β2Xq 2)(β1+2β2Xq)],B4=r2[r2(1-αcos(π/2)Xq)(1+β1Xq+β2Xq2)2-ν((α(π/2)2cos((π/2)Xq)(1+β1Xq+β2Xq2)2+6α(π/2)sin((π/2)Xq)(1+β1Xq+β2Xq2)(β1+2β2Xq)+6 (1-αcos(π/2)Xq) (β1+2β2Xq)2+6(1-αcos(π/2)Xq) (1+β1Xq+β2Xq2)β2)]-λ2].Thus, one obtains a homogeneous set of equations in terms of unknown constants a0,a1,a2,a3,a4,b0,b1,……..,bn-1, which, when written in matrix notation, takes the form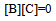 | (17) |
where[B] is an (n+1)x(n+5) matrix and[C] is an (n+5)x1 matrix.
4. Boundary Conditions and Frequency Equations
The frequency equations for clamped (C) and simply supported (S) rectangular plates have been obtained by employing the appropriate boundary conditions:C-S-C-S- PlatesFor a rectangular plate clamped at both the edges X=0 and X=1 (and simply supported at the remaining two edges),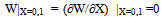 | (18) |
Applying the boundary conditions (18), to the deflection function (13), at the two edges X=0 and X=1, one obtains a set of four homogeneous equations in terms of unknown constants, which can be written as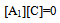 | (19) |
where[A1] is an 4x(n+5) matrix and[C] is an (n+5)x1 matrix.Equation (19), taken together with the equation (17), gives a complete set of (n+5) equations for a C-S-C-S- plate. These can be written as 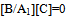 | (20) |
For a non-trivial solution of equation (20), the characteristic determinant must vanish: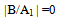 | (21) |
This is the frequency equation for a C-S-C-S- plate. S-S-S-S- PlatesFor a rectangular plate simply supported at both the edges X=0 and X=1 (and simply supported at the remaining two edges),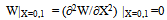 | (22) |
Employing the boundary conditions (22), to the deflection function (13), at the two edges X=0 and X=1, one gets the boundary equations for S-S-S-S- plate as 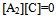 | (23) |
where[A2] is an 4x(n+5) matrix and[C] is an (n+5)x1 matrix.Hence frequency equation comes out for S-S-S-S- plate as 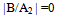 | (24) |
5. Results and Discussion
Frequency equations (21) and (24) are transcendental equations in λ2 from which infinitely many roots can be obtained. The frequency parameter λ corresponding to first three modes of vibration of C-S-C-S-and S-S-S-S-rectangular plates have been computed for m=1 and various values of thermal constant (α) , taper constants (β1, β2) for fixed aspect ratio (a/b=1.5). The value of Poisson ratio 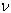 has been taken as 0.3.To choose the appropriate interpolation interval ΔX, the computer programme has been developed for the evaluation of the frequency parameter λ and run for n=10(5)60.The numerical values show a consistent improvement with the increase of the number of knots. In all the above computation, authors have fixed n=50, since further increase in n does not improve the results except in the fifth or sixth decimal places. These results have been tabulated in tables 1 to 3.The results presented in table 1 show a marked effect of variation of thermal constant (α) on the frequency parameter (λ) for different combinations of taper constant (β1, β2) and fixed aspect ratio (a/b = 1.5) corresponding the first three modes of vibration for C-S-C-S- and S-S-S-S- plates. The value of frequency parameter decrease with the increase of thermal constant for both the boundary conditions, considered here. Further, it can be seen from table that frequency parameter, for both the boundary conditions, decreases gradually in the third mode of vibrations in comparison to first two modes of vibration.Table 2 shows the variation of frequency parameter (λ) with taper constant (β1) for taper constant (β2=0.5) , two values of thermal constant (α=0.0, 0.4) and fixed aspect ratio (a/b = 1.5) corresponding to the first three modes of vibration. It is observed that the frequency parameter increases with the increase of taper constant for both the boundary conditions, considered here.In table 3, the effect of taper constant (β2) on frequency parameter for taper constant (β1=0.5), two values of thermal constant (α=0.0, 0.4) and fixed aspect ratio (a/b = 1.5) corresponding to the first three modes of vibration for C-S-C-S- and S-S-S-S- plates, have been shown. From this table, one can observe that frequency parameter in first three modes of vibration increases with the increase of taper constant for C-S-C-S- and S-S-S-S- plates.Further, it can be seen from tables 2 and 3 that frequency parameter , for both the boundary conditions, increases gradually in the third mode of vibrations in comparison to first two modes of vibration. Also, one can observe from tables 1 to 3, that frequency parameter of C-S-C-S- plate is higher than that of S-S-S-S- plate.
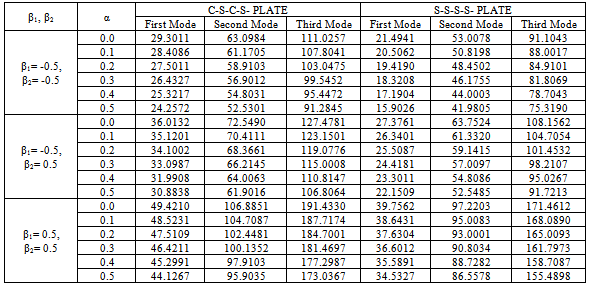
has been taken as 0.3.To choose the appropriate interpolation interval ΔX, the computer programme has been developed for the evaluation of the frequency parameter λ and run for n=10(5)60.The numerical values show a consistent improvement with the increase of the number of knots. In all the above computation, authors have fixed n=50, since further increase in n does not improve the results except in the fifth or sixth decimal places. These results have been tabulated in tables 1 to 3.The results presented in table 1 show a marked effect of variation of thermal constant (α) on the frequency parameter (λ) for different combinations of taper constant (β1, β2) and fixed aspect ratio (a/b = 1.5) corresponding the first three modes of vibration for C-S-C-S- and S-S-S-S- plates. The value of frequency parameter decrease with the increase of thermal constant for both the boundary conditions, considered here. Further, it can be seen from table that frequency parameter, for both the boundary conditions, decreases gradually in the third mode of vibrations in comparison to first two modes of vibration.Table 2 shows the variation of frequency parameter (λ) with taper constant (β1) for taper constant (β2=0.5) , two values of thermal constant (α=0.0, 0.4) and fixed aspect ratio (a/b = 1.5) corresponding to the first three modes of vibration. It is observed that the frequency parameter increases with the increase of taper constant for both the boundary conditions, considered here.In table 3, the effect of taper constant (β2) on frequency parameter for taper constant (β1=0.5), two values of thermal constant (α=0.0, 0.4) and fixed aspect ratio (a/b = 1.5) corresponding to the first three modes of vibration for C-S-C-S- and S-S-S-S- plates, have been shown. From this table, one can observe that frequency parameter in first three modes of vibration increases with the increase of taper constant for C-S-C-S- and S-S-S-S- plates.Further, it can be seen from tables 2 and 3 that frequency parameter , for both the boundary conditions, increases gradually in the third mode of vibrations in comparison to first two modes of vibration. Also, one can observe from tables 1 to 3, that frequency parameter of C-S-C-S- plate is higher than that of S-S-S-S- plate.Table 1. Value of frequency parameter (λ) for different values of thermal constant (α) with different combinations of taper constant (β1, β2) and fixed aspect ratio (a/b = 1.5) for C-S-C-S- and S-S-S-S- plate for first three modes of vibrations : m=1
 |
| |
|
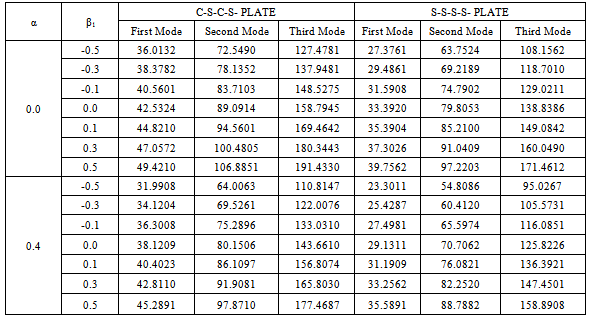
Table 2. Value of frequency parameter (λ) for different values of taper constant (β1) with different combinations of thermal constant ( α) and fixed aspect ratio (a/b = 1.5) for C-S-C-S- and S-S-S-S- plate for first three modes of vibrations : m=1 and β2=0.5
 |
| |
|
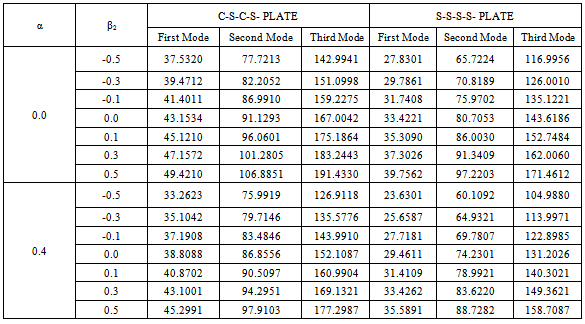
Table 3. Value of frequency parameter (λ) for different values of taper constant (β2) with different combinations of thermal constant ( α) and fixed aspect ratio (a/b = 1.5) for C-S-C-S- and S-S-S-S- plate for first three modes of vibrations :m=1 and β1=0.5
 |
| |
|
6. Conclusions
It can be concluded from the results that frequency parameter increases with increase in taper constants and decreases with increase in thermal gradient. Also, it is evident from the tables 2 and 3 that when β1=0.5, the values of frequency parameter more in comparison to β2=0.5 for all the three modes of vibrations and both the boundary conditions. It is also clear from the tables that third mode of vibration changes more sharply than second and first.
References
| [1] | Leissa AW. Vibration of Plates 1969. NASA-SP. |
| [2] | Leissa AW. Recent research in plate vibrations, 1973–1976: classical theory. Shock and Vibration Digest 1977; 9 (10): 13–24. |
| [3] | Leissa AW. Recent research in plate vibrations, 1973–1976: complicating effects. Shock and Vibration Digest 1978; 10 (12): 21–35. |
| [4] | Leissa AW. Recent research in plate vibrations, 1976–1980: complicating effects. Shock and Vibration Digest 1981; 13 (10): 19–36. |
| [5] | Leissa AW. Recent research in plate vibrations, 1981–1985: complicating effects. Shock and Vibration Digest 1987; 19 (3): 10–24. |
| [6] | Jain RK, Soni SR. Free vibrations of rectangular plates of parabolically varying thickness. Indian Journal of Pure and Applied Mathematics 1973; 4: 267-277. |
| [7] | Tomar JS, Gupta DC, Jain NC .Free vibrations of an isotropic non-homogeneous infinite plate of linearly varying thickness. Meccanica 1983; 18: 30-33. |
| [8] | Singh RP, Jain SK .Free asymmetric transverse vibration of parabolically varying thickness polar orthotropic annular plate with flexible edge conditions. Tamkang Journal of Science and Engineering 2004; 7(1): 41-52. |
| [9] | Kumar Y, Tomar SK. Free transverse vibrations of monoclinic rectangular plates with continuously varying thickness and density. International Journal of Applied Mechanics and Engineering 2006; 11(4): 881-900. |
| [10] | Gupta US, Lal R, Sharma S. Vibration analysis of non-homogeneous circular plate of nonlinear thickness variation by differential quadrature method. Journal of Sound and Vibration 2006; 298: 892-906. |
| [11] | Gupta AK, Johri T, Vats RP .Thermal effect on vibration of non-homogeneous orthotropic rectangular plate having bi-directional parabolically varying thickness. Proceeding of International Conference in World Congress on Engineering and Computer Science 2007, San-Francisco, USA, 24-26 Oct, 2007: 784-787. |
| [12] | Feng ZY, Min WZ. Vibrations of axially moving visco-elastic plate with parabolically varying thickness. Journal of Sound and Vibration 2008; 316: 198-210. |
| [13] | Gupta AK, Kumar A, Gupta YK. Vibration of visco-elastic parallelogram plate with parabolic thickness variation. Applied Mathematics 2010;1(2): 128-136. |
| [14] | Bhatnagar NS, Gupta AK. Vibration analysis of visco-elastic circular plate subjected to thermal gradient. Modelling Simulation and Control ‘B’ AMSE Press 1988; 15 (1): 17-31. |
| [15] | Gupta AK, Sharma P. Study the thermal gradient effect on frequencies of a trapezoidal plate of linearly varying thickness. Applied Mathematics 2010; 1(5): 357-365. |
| [16] | Gupta AK, Singhal P. Effect of non-homogeneity on thermally induced vibration of orthotropic visco-elastic rectangular plate of linearly varying thickness. Applied Mathematics 2010; 1(4): 326-333. |
| [17] | Tomar JS, Gupta AK. Effect of thermal gradient on frequencies of orthotropic rectangular plate whose thickness varies in two directions. Journal of Sound and Vibration 1985; 98 (2): 257-262. |
| [18] | Gupta AK, Khanna A .Vibration of visco-elastic rectangular plate with linearly thickness variations in both directions. Journal of Sound and Vibration 2007; 301(3-5): 450-457. |
| [19] | Gupta AK, Sharma S. Thermally induced vibration of orthotropic trapezoidal plate of linearly varying thickness. Journal of Vibration and Control 2011; 17(10):1591-1598. |
| [20] | Gupta AK, Sharma P . Effect of linear thermal gradient on vibration of trapezoidal plates whose thickness varies parabolically. Journal of Vibration and Control 2012; 18(3): 395-403. |
| [21] | Bickley WG. Piecewise cubic interpolation and two point boundary problems. The Computer Journal 1968; 11: 206–208. |
| [22] | Gupta AK, Sharma P. Study of thermally induced vibration of non-homogeneous trapezoidal plate with varying thickness and density. American Journal of Computational and Applied Mathematics 2012, 2(6): 265-275. |
| [23] | Olsson U. On free vibration at temperature dependent material properties and transient temperature fields. Journal of Applied Mechanics, Trans. ASME 1972; 39(3):723-726. |
| [24] | Nowacki W. Thermo elasticity, Pergamon Press, New York 1962 |

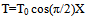
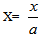 and T0 denotes the temperature excess above reference temperature at the end i.e. x=a or X=1.The temperature dependence of the modulus of elasticity for most of engineering materials is given by[24]:
and T0 denotes the temperature excess above reference temperature at the end i.e. x=a or X=1.The temperature dependence of the modulus of elasticity for most of engineering materials is given by[24]: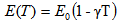
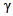 is the slope of the variation of E with T. Taking as the reference temperature, the temperature at the end of plate i.e. at X=1, the modulus variation in view of (1) and (2), becomes
is the slope of the variation of E with T. Taking as the reference temperature, the temperature at the end of plate i.e. at X=1, the modulus variation in view of (1) and (2), becomes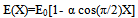
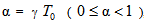 , a constant known as temperature constant.The differential equation governing the free transverse motion of an elastic rectangular plate of length a, breadth b, thickness h and density ρ is
, a constant known as temperature constant.The differential equation governing the free transverse motion of an elastic rectangular plate of length a, breadth b, thickness h and density ρ is 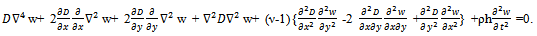
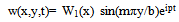
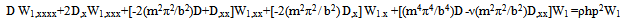
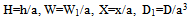
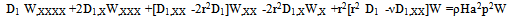
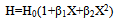
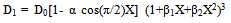
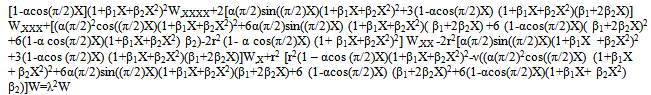
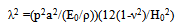
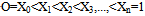 .Let the approximating function W(X) for f(X) be a quintic spline with the following properties :(a) W(X) is a quintic polynomial in each interval (Xk, Xk+1),(b) W(Xk) =f(Xk), k = 0 (1) n,(c) W’(X), W”(X), W’’’(X) and Wiv(X) are continuous.From the definition, a quintic spline takes the form
.Let the approximating function W(X) for f(X) be a quintic spline with the following properties :(a) W(X) is a quintic polynomial in each interval (Xk, Xk+1),(b) W(Xk) =f(Xk), k = 0 (1) n,(c) W’(X), W”(X), W’’’(X) and Wiv(X) are continuous.From the definition, a quintic spline takes the form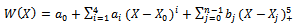
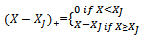
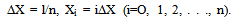
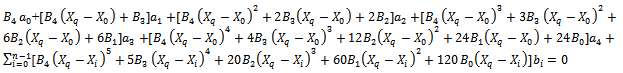
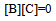
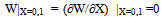
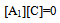
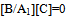
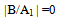
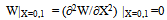
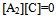
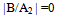
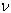 has been taken as 0.3.To choose the appropriate interpolation interval ΔX, the computer programme has been developed for the evaluation of the frequency parameter λ and run for n=10(5)60.The numerical values show a consistent improvement with the increase of the number of knots. In all the above computation, authors have fixed n=50, since further increase in n does not improve the results except in the fifth or sixth decimal places. These results have been tabulated in tables 1 to 3.The results presented in table 1 show a marked effect of variation of thermal constant (α) on the frequency parameter (λ) for different combinations of taper constant (β1, β2) and fixed aspect ratio (a/b = 1.5) corresponding the first three modes of vibration for C-S-C-S- and S-S-S-S- plates. The value of frequency parameter decrease with the increase of thermal constant for both the boundary conditions, considered here. Further, it can be seen from table that frequency parameter, for both the boundary conditions, decreases gradually in the third mode of vibrations in comparison to first two modes of vibration.Table 2 shows the variation of frequency parameter (λ) with taper constant (β1) for taper constant (β2=0.5) , two values of thermal constant (α=0.0, 0.4) and fixed aspect ratio (a/b = 1.5) corresponding to the first three modes of vibration. It is observed that the frequency parameter increases with the increase of taper constant for both the boundary conditions, considered here.In table 3, the effect of taper constant (β2) on frequency parameter for taper constant (β1=0.5), two values of thermal constant (α=0.0, 0.4) and fixed aspect ratio (a/b = 1.5) corresponding to the first three modes of vibration for C-S-C-S- and S-S-S-S- plates, have been shown. From this table, one can observe that frequency parameter in first three modes of vibration increases with the increase of taper constant for C-S-C-S- and S-S-S-S- plates.Further, it can be seen from tables 2 and 3 that frequency parameter , for both the boundary conditions, increases gradually in the third mode of vibrations in comparison to first two modes of vibration. Also, one can observe from tables 1 to 3, that frequency parameter of C-S-C-S- plate is higher than that of S-S-S-S- plate.
has been taken as 0.3.To choose the appropriate interpolation interval ΔX, the computer programme has been developed for the evaluation of the frequency parameter λ and run for n=10(5)60.The numerical values show a consistent improvement with the increase of the number of knots. In all the above computation, authors have fixed n=50, since further increase in n does not improve the results except in the fifth or sixth decimal places. These results have been tabulated in tables 1 to 3.The results presented in table 1 show a marked effect of variation of thermal constant (α) on the frequency parameter (λ) for different combinations of taper constant (β1, β2) and fixed aspect ratio (a/b = 1.5) corresponding the first three modes of vibration for C-S-C-S- and S-S-S-S- plates. The value of frequency parameter decrease with the increase of thermal constant for both the boundary conditions, considered here. Further, it can be seen from table that frequency parameter, for both the boundary conditions, decreases gradually in the third mode of vibrations in comparison to first two modes of vibration.Table 2 shows the variation of frequency parameter (λ) with taper constant (β1) for taper constant (β2=0.5) , two values of thermal constant (α=0.0, 0.4) and fixed aspect ratio (a/b = 1.5) corresponding to the first three modes of vibration. It is observed that the frequency parameter increases with the increase of taper constant for both the boundary conditions, considered here.In table 3, the effect of taper constant (β2) on frequency parameter for taper constant (β1=0.5), two values of thermal constant (α=0.0, 0.4) and fixed aspect ratio (a/b = 1.5) corresponding to the first three modes of vibration for C-S-C-S- and S-S-S-S- plates, have been shown. From this table, one can observe that frequency parameter in first three modes of vibration increases with the increase of taper constant for C-S-C-S- and S-S-S-S- plates.Further, it can be seen from tables 2 and 3 that frequency parameter , for both the boundary conditions, increases gradually in the third mode of vibrations in comparison to first two modes of vibration. Also, one can observe from tables 1 to 3, that frequency parameter of C-S-C-S- plate is higher than that of S-S-S-S- plate. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML

