-
Paper Information
- Next Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Computational and Applied Mathematics
p-ISSN: 2165-8935 e-ISSN: 2165-8943
2013; 3(2): 97-105
doi:10.5923/j.ajcam.20130302.07
Analytical Soliton Solutions and Wave Solutions of Discrete Nonlinear Cubic-Quintique Ginzburg-Landau Equations in Array of Dissipative Optical Systems
Jean Roger Bogning
Department of Physics, Higher Teacher’s Training College, University of Bamenda, PO Box 39, Bamenda, Cameroon
Correspondence to: Jean Roger Bogning, Department of Physics, Higher Teacher’s Training College, University of Bamenda, PO Box 39, Bamenda, Cameroon.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
In this work, we are looking for the wave solutions and soliton solutions of some discrete nonlinear partial differential equations in order to integrate the discrete variable 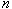 in the expression of amplitude and phase. Hence We choose for this reason the networks of dispersive optical systems where the dynamics of propagation of waves is governed by the discrete nonlinear partial differential equations of Ginzburg-Landau types. With the help of some innovative and suitable transformations, we uncouple the equations to solve in order to get the ones that govern the dynamics of phase and amplitude, hereby facilitating the achievement of our goal. The expressions of the non linear phases are also obtained as well.
in the expression of amplitude and phase. Hence We choose for this reason the networks of dispersive optical systems where the dynamics of propagation of waves is governed by the discrete nonlinear partial differential equations of Ginzburg-Landau types. With the help of some innovative and suitable transformations, we uncouple the equations to solve in order to get the ones that govern the dynamics of phase and amplitude, hereby facilitating the achievement of our goal. The expressions of the non linear phases are also obtained as well.
Keywords: Discrete , Nonlinear, Ginzburg-Landau, Phase Soliton, Pulse Soliton, Soliton Solutions
Cite this paper: Jean Roger Bogning, Analytical Soliton Solutions and Wave Solutions of Discrete Nonlinear Cubic-Quintique Ginzburg-Landau Equations in Array of Dissipative Optical Systems, American Journal of Computational and Applied Mathematics , Vol. 3 No. 2, 2013, pp. 97-105. doi: 10.5923/j.ajcam.20130302.07.
Article Outline
1. Introduction
- Great deals of physical systems are governed by mathematical equations, notably the linear differential equations, linear partial differential equations, and the discrete nonlinear partial differential equations or discrete nonlinear ordinary equations which describe the complicated physical systems. A better knowledge of these physical systems, require the numerical resolution and above all the analytical resolution of these equations. This justifies especially the determination of physicists to continue their research of the physical solutions, or the solutions which are closed to reality. In the last few decades, many authors have been interested in the discrete model equations[1-5]. The best techniques of resolution have been discovered or improved; others have been used to give the solutions of different mathematical and nonlinear physical equations [6-18]. Very often it is the future wave named soliton that is in the center of several nonlinear partial differential equations resolution.It has caused a lot of interest in the minds of most researchers resulting in a series of publications[19-25]. In optical fibers and other domains, researchers brought forward the solutions of the equations and treat the nonlinear dynamic excitations[26-38]. In short the interest of the researchers in resolving of the partial differential equations and in the nonlinear partial differential equations is more and more crescent according. If the spatio-temporal nonlinear partial differential equations (NPDE) is not comfortable to solve, the one of the discrete NPDE is even more complicated. It is due to the fact that in addition to the spatial and temporal variables, we must use another variable which determines the number of elements that the network contains. Speaking of the network, a great deal of the discrete NPDEs describe the dynamics of propagation of waves in the networks like optical fibers, atomic chains, and electric lines,… and so on and so forth. But the problem remains how to find wave solutions of the shape
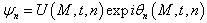 where
where 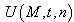 represents the envelope of the wave and
represents the envelope of the wave and 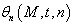 the phase,
the phase, 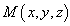 a point of space,
a point of space, 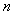 the discrete variable and
the discrete variable and 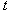 the time. i.e. to find a solution that takes into account the discrete variable in the amplitude. If a lot of research works yields many solutions under the shape
the time. i.e. to find a solution that takes into account the discrete variable in the amplitude. If a lot of research works yields many solutions under the shape 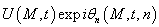 where the amplitude is a function of space and time, there are few cases where the amplitude is a function of space, time and discrete variable
where the amplitude is a function of space and time, there are few cases where the amplitude is a function of space, time and discrete variable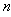 . In our previous works, we demonstrated that it was possible to transform the discrete NPDE with the help of the recurrence relations which govern the phase[37]. This method will be put in evidence in this work that is to look for the solutions of the discrete complex Ginzburg-Landau equations in dissipative mode. The NPDEs considered here take into account the temporal and discrete variable. The solutions that we are going to propose will have the shape
. In our previous works, we demonstrated that it was possible to transform the discrete NPDE with the help of the recurrence relations which govern the phase[37]. This method will be put in evidence in this work that is to look for the solutions of the discrete complex Ginzburg-Landau equations in dissipative mode. The NPDEs considered here take into account the temporal and discrete variable. The solutions that we are going to propose will have the shape 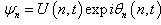 where
where 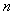 is the discrete variable and the time. Hereafter, we find the analytical soliton solutions of the discrete cubic-quintique nonlinear and complex Ginzburg - Landau equation by the right method (see ref.[37]). This method consists of bounding the equation by the lower bound and upper bound equations, and after obtaining the induction relation which governs the phases of the solutions. We obtained these induction relations by finding the values which give out
is the discrete variable and the time. Hereafter, we find the analytical soliton solutions of the discrete cubic-quintique nonlinear and complex Ginzburg - Landau equation by the right method (see ref.[37]). This method consists of bounding the equation by the lower bound and upper bound equations, and after obtaining the induction relation which governs the phases of the solutions. We obtained these induction relations by finding the values which give out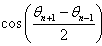 ,
, 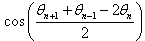 and
and 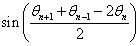 max. Then the solutions obtained take into account the discrete number
max. Then the solutions obtained take into account the discrete number  , the real time of propagation
, the real time of propagation  and the time delay due to the influence of other fibers on the considered propagating fiber.This paper is organized as follows. In section 2, we introduced the method to be used, in section 3, we apply this method on Ablowitz-Ladik’s equation which is a single nonlinear cubic and integrable Schrödinger equation. Section 4, proposes the analytical solutions of the dissipative discrete cubic nonlinear complex Ginzburg-Landau equation. Section 5, proposes the analytical solutions of the dissipative discrete cubic-quintique nonlinear complexGinzburg-Landau[25], section 6 proposes the analytical solutions of the discrete cubic nonlinear complex Ginzburg-Landau equation in the dissipative model with nonlinear terms
and the time delay due to the influence of other fibers on the considered propagating fiber.This paper is organized as follows. In section 2, we introduced the method to be used, in section 3, we apply this method on Ablowitz-Ladik’s equation which is a single nonlinear cubic and integrable Schrödinger equation. Section 4, proposes the analytical solutions of the dissipative discrete cubic nonlinear complex Ginzburg-Landau equation. Section 5, proposes the analytical solutions of the dissipative discrete cubic-quintique nonlinear complexGinzburg-Landau[25], section 6 proposes the analytical solutions of the discrete cubic nonlinear complex Ginzburg-Landau equation in the dissipative model with nonlinear terms 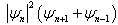 and
and 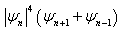 . Finally, section 7 concludes with brief comments.
. Finally, section 7 concludes with brief comments.2. Method
- The main principle behind this method consists of introducing in the equation to solve as a solution of the shape
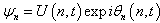
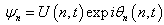 . It leads to coupled equations in
. It leads to coupled equations in 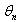 and
and 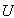 . While transforming
. While transforming 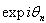 according to the Moivre’s formula, the resulting equations can be shown under shapes that include the terms in
according to the Moivre’s formula, the resulting equations can be shown under shapes that include the terms in 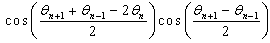 ,
, 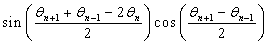 or
or 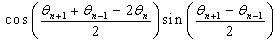 ,…, and so on and so forth. The presence of the expressions of this nature, allows obtaining the bounded equations which are limited by two other equations of which one is lower bound and the other is upper bound. Following these observations, we note that to have the lower bound equation or upper bound equation result in the following correspondences
,…, and so on and so forth. The presence of the expressions of this nature, allows obtaining the bounded equations which are limited by two other equations of which one is lower bound and the other is upper bound. Following these observations, we note that to have the lower bound equation or upper bound equation result in the following correspondences 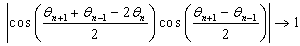 ,
, 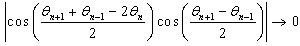 or
or 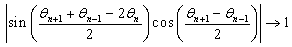 and so forth. These correspondences permit the recurrence relations that govern
and so forth. These correspondences permit the recurrence relations that govern  of which the resulting equations, end with the expressions of
of which the resulting equations, end with the expressions of  and
and  which are the first term of
which are the first term of 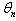 when
when 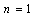 (
(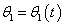 ). What is also important to mention here is that, we want amplitude
). What is also important to mention here is that, we want amplitude 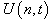 that is effectively a function of
that is effectively a function of 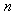 . To arrive there, we put the change of variable
. To arrive there, we put the change of variable 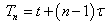 where
where 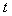 is the effective time cover by the wave in a considered propagator fiber or cell of the network without the influence of the neighbors,
is the effective time cover by the wave in a considered propagator fiber or cell of the network without the influence of the neighbors, 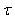 the time delay imposed by the neighboring fibers or neighboring cells on the propagator fiber or cell if one supposes that the contribution of every fiber is the same and is worth
the time delay imposed by the neighboring fibers or neighboring cells on the propagator fiber or cell if one supposes that the contribution of every fiber is the same and is worth 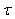 ,
, 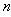 represents the number of fibers or cells that the network contains.
represents the number of fibers or cells that the network contains. 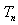 can take various shapes, for example
can take various shapes, for example 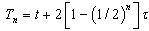 if the delay time imposed by every fiber or cell varies according to the remoteness with respect to the propagator fiber as a geometric regression of common ratio
if the delay time imposed by every fiber or cell varies according to the remoteness with respect to the propagator fiber as a geometric regression of common ratio 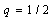 . In the course of this work, we are going to use this method to propose solutions of some discrete NPDEs of Ginzburg-Landau in dissipative media.
. In the course of this work, we are going to use this method to propose solutions of some discrete NPDEs of Ginzburg-Landau in dissipative media. 3. Cubic Nonlinear Schrödinger Equation
- We use the cubic integrable Schrödinger equation (Ablowitz-Ladik)[38] given by the following relation
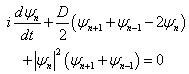 | (1) |
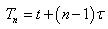 , where
, where 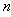 is the number of fibers or cores,
is the number of fibers or cores, 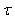 the time delay due to one fiber or core and
the time delay due to one fiber or core and 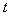 the real time of propagation in the absence of neighboring fibers. The equation (1) becomes
the real time of propagation in the absence of neighboring fibers. The equation (1) becomes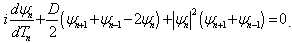 | (2) |
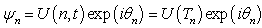 | (3) |
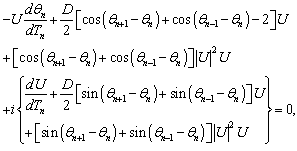 | (4) |
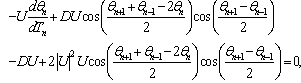 | (5) |
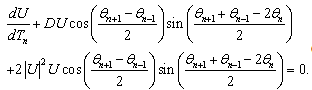 | (6) |
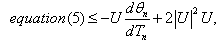 | (7) |
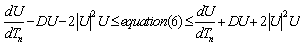 | (8) |
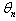 are maximum or minimum. If we consider the case where
are maximum or minimum. If we consider the case where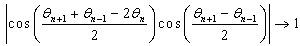 , then the following relations are verified
, then the following relations are verified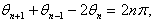 | (9) |
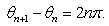 | (10) |
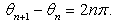 | (11) |
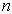 varies the equation (11) yields
varies the equation (11) yields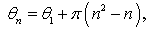 | (12) |
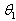 represents the expression of
represents the expression of 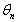 when
when 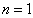 .The substitution of equation (12) into equation (5) and equation (6) yields the reduced system of equations
.The substitution of equation (12) into equation (5) and equation (6) yields the reduced system of equations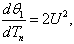 | (13) |
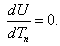 | (14) |
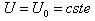 ,
, 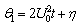 (because for
(because for 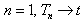 ). In this case the solution of equation (1) is given by
). In this case the solution of equation (1) is given by 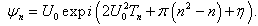 | (15) |
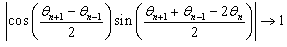 , then we obtain
, then we obtain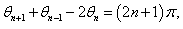 | (16) |
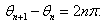 | (17) |
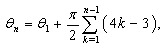 | (18) |
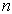 describes the set of natural numbers and
describes the set of natural numbers and 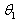 is the expression of
is the expression of 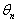 when
when 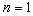 . When
. When 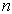 varies equation (18) is written
varies equation (18) is written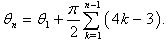 | (19) |
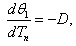 | (20) |
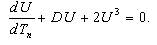 | (21) |
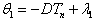 , where
, where 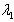 is an arbitrary constant,
is an arbitrary constant, 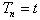 because
because 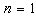 and the equation (19) becomes
and the equation (19) becomes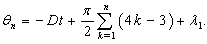 | (22) |
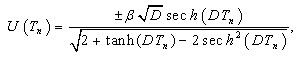 | (23) |
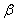 is an arbitrary constant and
is an arbitrary constant and 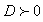 . From equations (1), (2), (22) and equation (23) we can therefore write the solution of equation (1) as
. From equations (1), (2), (22) and equation (23) we can therefore write the solution of equation (1) as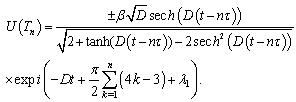 | (24) |
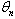 . But in the course of this work, we are going to consider that
. But in the course of this work, we are going to consider that 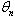 is under the shape
is under the shape 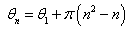 , where
, where 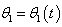 .
.4. Solutions of Dissipative Cubic Nonlinear Complex Ginzburg-Landau Equation
- In this section, we consider the cubic nonlinear complex Ginzburg-landau equation in the dissipative system[24] given by
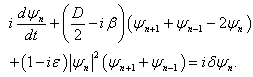 | (25) |
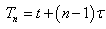 , we rewrite equation (25) in the form
, we rewrite equation (25) in the form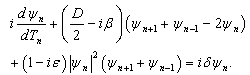 | (26) |
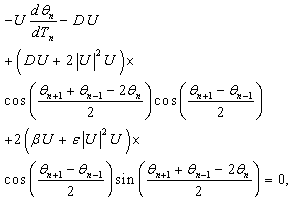 | (27) |
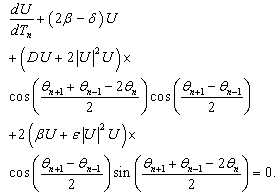 | (28) |
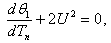 | (29) |
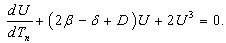 | (30) |
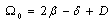 , and according to the fact that
, and according to the fact that 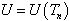 we rewrite equation (29) and equation (30) as
we rewrite equation (29) and equation (30) as 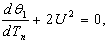 | (31) |
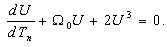 | (32) |
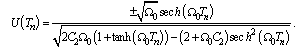 | (33) |
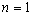
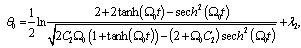 | (34) |
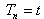 ,
, 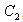 ,
, 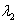 are the arbitrary constants. From equation (34) and equation (12) we obtain the following relation
are the arbitrary constants. From equation (34) and equation (12) we obtain the following relation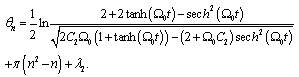 | (35) |
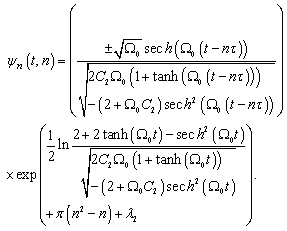 | (36) |
5. Solutions of Dissipative Complex Cubic-Quintique Nonlinear Ginzburg-Landau Equation
- The equation that we consider here is practically the one that we used in section 3 but with quintique nonlinearity. This equation is given by
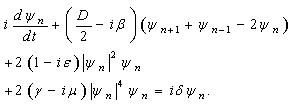 | (37) |
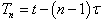 , it follows from equation (37) that
, it follows from equation (37) that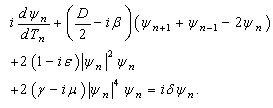 | (38) |
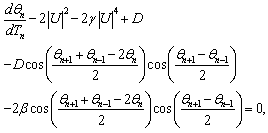 | (39) |
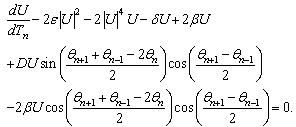 | (40) |
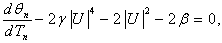 | (41) |
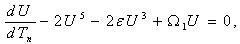 | (42) |
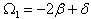 . Looking for general solution of equation (42), it follows that U verify the relation
. Looking for general solution of equation (42), it follows that U verify the relation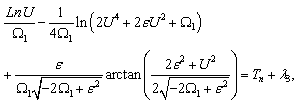 | (43) |
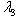 is the arbitrary constant. To obtain
is the arbitrary constant. To obtain 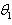 in this case, we introduce the value of
in this case, we introduce the value of 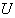 given by equation (43) in equation (41). But it will be very difficult to obtain the general expression of
given by equation (43) in equation (41). But it will be very difficult to obtain the general expression of 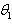 . Nevertheless, we can obtain solutions of equation (41) and (42) by imputing values to different constants
. Nevertheless, we can obtain solutions of equation (41) and (42) by imputing values to different constants 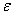 ,
, 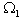 ,
, 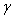 and
and 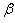 . By considering the case where
. By considering the case where 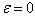 ,
, 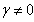 and
and 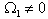 , the system form by equation (41) and (42) becomes
, the system form by equation (41) and (42) becomes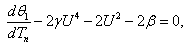 | (44) |
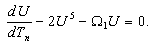 | (45) |
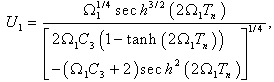 | (46) |
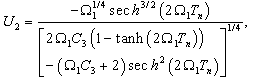 | (47) |
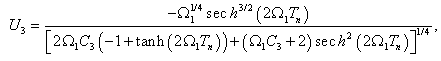 | (48) |
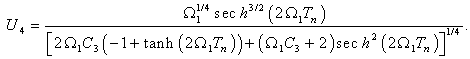 | (49) |
 correspond to
correspond to 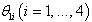 and naturally the final expression of
and naturally the final expression of 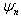 . Then, taking into account equation (46) into equation (44), we obtain
. Then, taking into account equation (46) into equation (44), we obtain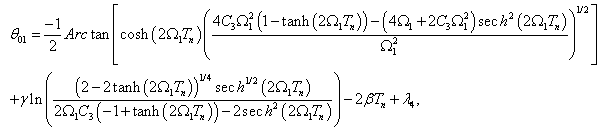 | (50) |
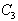 ,
, 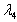 are constants,
are constants, 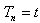 . From equation (46) and equation (50), we deduce one particular solution of equation (37)
. From equation (46) and equation (50), we deduce one particular solution of equation (37)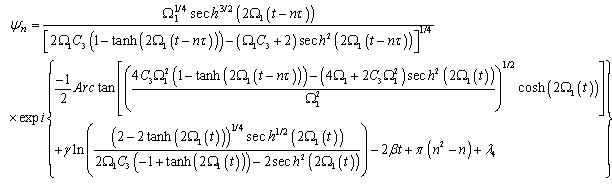 | (51) |
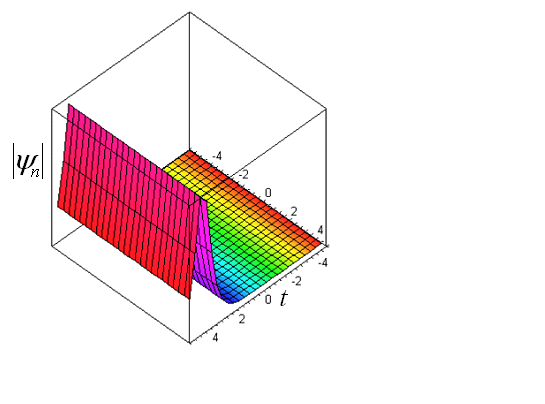 | Figure 1. Representative curve of the intensity of the wave given by the equation(51) for 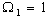 , , 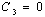 , , 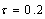 and and 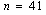 |
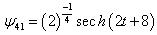 ; which is logically the analytical shape of a pulse. But when one observes Figure 1, one surrenders to the evidence that it is a pulse that has undergone distortions with respect to a classic pulse. This distortion can be interpreted as due to the influence of the number of fibers “
; which is logically the analytical shape of a pulse. But when one observes Figure 1, one surrenders to the evidence that it is a pulse that has undergone distortions with respect to a classic pulse. This distortion can be interpreted as due to the influence of the number of fibers “ ” that we took into account in the expression of the amplitude of the equation (51).
” that we took into account in the expression of the amplitude of the equation (51). 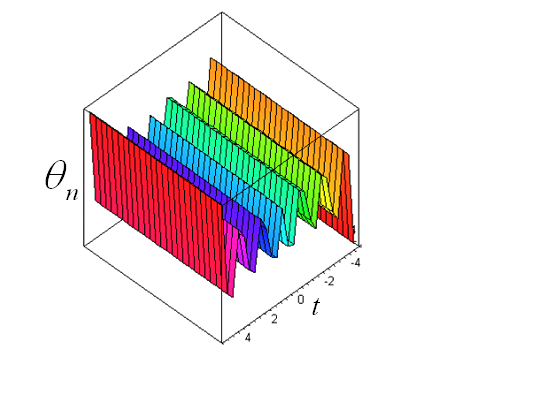 | Figure 2. Representative curve of the phase 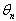 of the wave given by the equation(51) for of the wave given by the equation(51) for 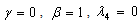 and and 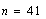 |
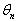 of the solution given by the equation (51) according to time. We note that this profile of phase is all specific and at such we can ask ourselves the question if we are always right every time and on any type of equation to suppose that the phases of the solutions to construct are linear in temporal variable and in spatial variable?As we progress with our analysis, we are going to seek solutions of complex cubic-quintique nonlinear Ginzburg-Landau equation which contains the additive terms
of the solution given by the equation (51) according to time. We note that this profile of phase is all specific and at such we can ask ourselves the question if we are always right every time and on any type of equation to suppose that the phases of the solutions to construct are linear in temporal variable and in spatial variable?As we progress with our analysis, we are going to seek solutions of complex cubic-quintique nonlinear Ginzburg-Landau equation which contains the additive terms 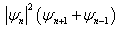 and
and 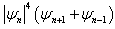 .
.6. Solutions of Dissipative Complex Cubic-Quintique Nonlinear Ginzburg-Landau Equation Containing the Terms 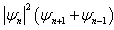 and
and 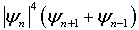
- In this section of work, the equation which will be in the center of our analysis has the following shape
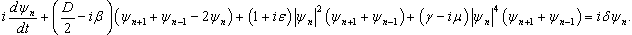 | (52) |
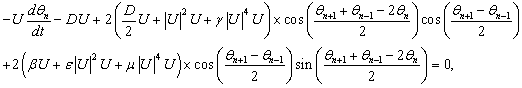 | (53) |
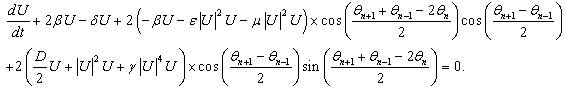 | (54) |
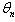 established at the beginning of this work. So when
established at the beginning of this work. So when 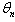 takes
takes 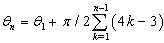 , equation (53) and equation (54) yield the system of coupled equations analogous to the system obtained in equation (41) and equation (42) which is already solved . Then we focus our attention in the case where
, equation (53) and equation (54) yield the system of coupled equations analogous to the system obtained in equation (41) and equation (42) which is already solved . Then we focus our attention in the case where 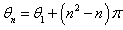 . With this transformation equation (53) and (54) give respectively
. With this transformation equation (53) and (54) give respectively 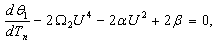 | (55) |
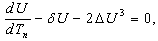 | (56) |
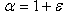 ,
, 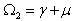 and
and 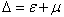 , we obtain via the resolution of equation (56)
, we obtain via the resolution of equation (56)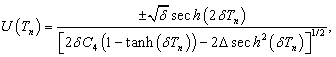 | (57) |
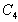 is the arbitrary constant. The substitution of equation (57) into equation (55) leads to
is the arbitrary constant. The substitution of equation (57) into equation (55) leads to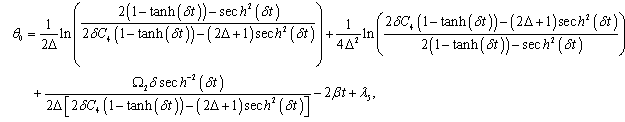 | (58) |
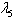 is an arbitrary constant. Finally the solution of equation (52) is given by
is an arbitrary constant. Finally the solution of equation (52) is given by 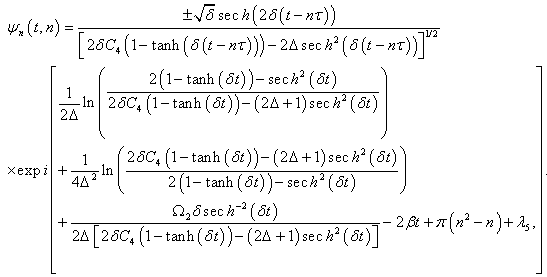 | (59) |
7. Conclusions
- The main objective of this research work was to bring forward wave solutions of some discrete nonlinear partial differential equations so that the discrete variable "
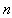 " is taken simultaneously into account in the expression of amplitude and phase; what is often very difficult to achieve. We believe that this objective has been attained with different supports of analyses considered hereafter. We want to speak here of Ginzburg-Landau equations presenting the different shapes of nonlinearities (cubic and quintique). Another merit of this work is to enable us to have the phases that are different from the classical phases and linear phases used fluently. The linear phase use fluently is for the shape
" is taken simultaneously into account in the expression of amplitude and phase; what is often very difficult to achieve. We believe that this objective has been attained with different supports of analyses considered hereafter. We want to speak here of Ginzburg-Landau equations presenting the different shapes of nonlinearities (cubic and quintique). Another merit of this work is to enable us to have the phases that are different from the classical phases and linear phases used fluently. The linear phase use fluently is for the shape 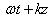 or
or 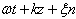 . These results indicate merely that it is possible to consider some wave solutions with phases that have other shapes like
. These results indicate merely that it is possible to consider some wave solutions with phases that have other shapes like 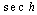 ,
, 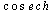 ,
, 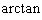 ,
, 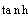 ,
, 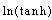 ,…, and so forth according to the goal that one wishes to attain. Another important report made is that the taking into account of the discrete variable in the amplitude expressions influences its profile considerably. We polish up our work by pointing out that solutions of discrete non linear partial differential equations obtained as in this article can to a greater extend provide with factors that influence the propagation of signals in the transmission network, notably the phenomena of multiple instabilities and intrinsic dissipations.
,…, and so forth according to the goal that one wishes to attain. Another important report made is that the taking into account of the discrete variable in the amplitude expressions influences its profile considerably. We polish up our work by pointing out that solutions of discrete non linear partial differential equations obtained as in this article can to a greater extend provide with factors that influence the propagation of signals in the transmission network, notably the phenomena of multiple instabilities and intrinsic dissipations.ACKNOWLEDGEMENTS
- We acknowledge support from the ministry of Higher Education of Cameroon through its program of support to research, which enabled us to carry out this work. We also thank Mr Kenfack Christopher Nguimatio for some corrections after the reading of the work.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML