Muhammad Younis1, Asim Zafar1, Kalim Ul-Haq2, Muhammad Rahman2
1Centre for Undergraduate Studies, University of the Punjab Lahore, Pakistan
2Department of Mathematics, Mirpur University of Science and Technology, Mirpur AJ & K
Correspondence to: Muhammad Younis, Centre for Undergraduate Studies, University of the Punjab Lahore, Pakistan.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
In this article, the 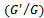 -expansion method has been implemented to find the new travelling wave solutions of nonlinear evolution equations of fractional order. For this, the fractional complex transformation method has been used to convert fractional order partial differential equation to ordinary differential equation. Then,
-expansion method has been implemented to find the new travelling wave solutions of nonlinear evolution equations of fractional order. For this, the fractional complex transformation method has been used to convert fractional order partial differential equation to ordinary differential equation. Then, 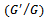 -expansion method has been implemented to celebrate the series of new travelling wave solutions to fractional order coupled Burgers’ equations.
-expansion method has been implemented to celebrate the series of new travelling wave solutions to fractional order coupled Burgers’ equations.
Keywords:
Travelling Wave Solutions, Fractional Complex Transformation, 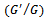 -Expansion Method, Fractional Calculus, Nonlinear Coupled Burgers’ Equations
-Expansion Method, Fractional Calculus, Nonlinear Coupled Burgers’ Equations
Cite this paper: Muhammad Younis, Asim Zafar, Kalim Ul-Haq, Muhammad Rahman, Travelling Wave Solutions of Fractional Order Coupled Burgers’ Equations by 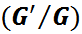 -Expansion Method, American Journal of Computational and Applied Mathematics , Vol. 3 No. 2, 2013, pp. 81-85. doi: 10.5923/j.ajcam.20130302.04.
-Expansion Method, American Journal of Computational and Applied Mathematics , Vol. 3 No. 2, 2013, pp. 81-85. doi: 10.5923/j.ajcam.20130302.04.
1. Introduction
Nonlinear evolution equations have been the area under discussion in different branches of mathematical and physical sciences such as physics, biology, chemistry, etc. The analytical solutions of such equations are of fundamental importance since a lot of mathematical and physical models are described by the nonlinear evolution equations. Among the possible solutions nonlinear evolution equations, certain special form solutions may depend only on a single combination of variables such as travelling wave variables.Knowing the importance of nonlinear evolution equations, in the literature, the variety of approaches exist to find the travelling wave and numerical solutions to nonlinear problems. Some of its cited here, the adomian decomposition method[7] and generalized differential transform method[8] have been used to find the numerical solutions for the space- and time-fractional coupled Burgers’ equations. The 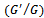 expansion method was introduced, by Wang et al.[6], to find the travelling wave solutions of nonlinear evolution equations. This method was further extended[9] to find the solutions of fractional order differential equations. The Jacobi elliptic function expansion method[10], the tanh-function method for finding solitary wave solutions[11], the homotopy perturbation method[12] have been applied to handle the nonlinear evolution equations etc.In this article, a new approach has been used to find the series of travelling wave solutions to nonlinear evolution equations of fractional order using the fractional complex transformation[3] and the
expansion method was introduced, by Wang et al.[6], to find the travelling wave solutions of nonlinear evolution equations. This method was further extended[9] to find the solutions of fractional order differential equations. The Jacobi elliptic function expansion method[10], the tanh-function method for finding solitary wave solutions[11], the homotopy perturbation method[12] have been applied to handle the nonlinear evolution equations etc.In this article, a new approach has been used to find the series of travelling wave solutions to nonlinear evolution equations of fractional order using the fractional complex transformation[3] and the 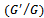 -expansion method[6], in the sense of Jumarie’s modified Riemann-Liouville derivative. For this, we first use the fractional complex transformation to convert into ordinary differential equations. Then, the obtained ODE has been converted into
-expansion method[6], in the sense of Jumarie’s modified Riemann-Liouville derivative. For this, we first use the fractional complex transformation to convert into ordinary differential equations. Then, the obtained ODE has been converted into 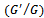 polynomial form. Using the homogenous balance and second order linear ordinary differential equation
polynomial form. Using the homogenous balance and second order linear ordinary differential equation 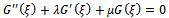 with the aid of computation, the new travelling wave solutions of
with the aid of computation, the new travelling wave solutions of 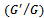 polynomial form has been calculated. As application the nonlinear coupled Burgers’ equations[6] with time-space fractional derivatives has been considered, which has the following form:
polynomial form has been calculated. As application the nonlinear coupled Burgers’ equations[6] with time-space fractional derivatives has been considered, which has the following form: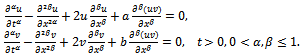 | (1.1) |
The rest of the article is organized as follows, in section 2 the basic definitions and properties for the fractional calculus are being considered regarding to modified Riemann-Liouville derivative. In section 3, the extended 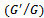 -expansion method has been proposed to find the new travelling wave solutions for NPDEs of fractional order with the help of fractional complex transformation. As an application, the new travelling wave solutions of nonlinear coupled Burgers’ equations have been discussed in section 4. In the last section 5, the conclusion has been drawn.
-expansion method has been proposed to find the new travelling wave solutions for NPDEs of fractional order with the help of fractional complex transformation. As an application, the new travelling wave solutions of nonlinear coupled Burgers’ equations have been discussed in section 4. In the last section 5, the conclusion has been drawn.
2. Background on Fractional Calculus
In this section, the proposed method has been applied in the sense of the Jumarie’s modified Riemann-Liouville derivative[4] of order α. For this, some basic definitions and properties of the fractional calculus theory are being considered (for details see[5]). Thus, the fractional derivatives can be defined following[4] as: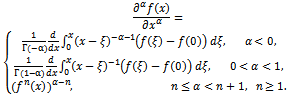 | (2.1) |
Moreover, some properties for the modified Riemann-Liouville derivative have also been given as follows: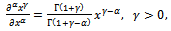 | (2.2) |
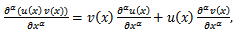 | (2.3) |
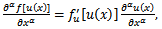 | (2.4) |
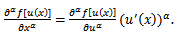 | (2.5) |
As far as concerned about the above results (2.3)–(2.5), the function 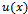 is said to be non-differentiable in equations (2.3) and (2.4) and it is differentiable in (2.5). The function
is said to be non-differentiable in equations (2.3) and (2.4) and it is differentiable in (2.5). The function 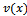 is non-differentiable, and
is non-differentiable, and 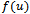 is differentiable in (2.4) and non-differentiable in (2.5). Thus, the formulas (2.3)–(2.5) should be used carefully.In view of[2, 3], the fractional complex transformation can be defined as follows:
is differentiable in (2.4) and non-differentiable in (2.5). Thus, the formulas (2.3)–(2.5) should be used carefully.In view of[2, 3], the fractional complex transformation can be defined as follows: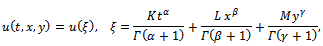 It helps to convert the partial differential equation of fractional order into an ordinary differential equation in very simple and easy manner (where K, L and M are non-zero arbitrary constants). In the following section, the
It helps to convert the partial differential equation of fractional order into an ordinary differential equation in very simple and easy manner (where K, L and M are non-zero arbitrary constants). In the following section, the 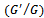 -expansion method has been described to find the travelling wave solutions.
-expansion method has been described to find the travelling wave solutions.
3. Description of the 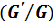 -Expansion Method
-Expansion Method
The 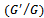 -expansion method[6], can be performed using the following steps. For this, we consider the following NPDE (nonlinear partial differential equation) of fractional order
-expansion method[6], can be performed using the following steps. For this, we consider the following NPDE (nonlinear partial differential equation) of fractional order 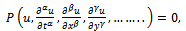 | (3.1) |
where u is an unknown function and P is a polynomial of u and its partial fractional derivatives along with the involvement of higher order derivatives and nonlinear terms.Step 1: First, we convert the NPDE of fractional order into nonlinear ordinary differential equations using the fractional complex transformation (2.6) introduced by Li et al.[3]. Hence, the travelling wave variable, defined in equation (2.6), permits us to reduce equation (3.1) to an ODE of 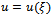 in the following form
in the following form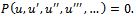 | (3.2) |
If the possibility occurs, then equation (3.2) can be integrated term by term once or more times.Step 2: Suppose that the solution of equation (3.2) can be expressed as a polynomial of 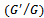 in the form:
in the form: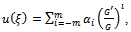 | (3.3) |
where 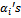 are constants and satisfies the following second order linear ordinary differential equation
are constants and satisfies the following second order linear ordinary differential equation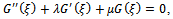 | (3.4) |
where 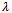 and
and 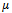 are constantsStep 3: The homogeneous balance technique can be used, to determine the positive integer m, between the highest order derivatives and the nonlinear terms appearing in (3.2). After the substitution of (3.3) into (3.2) and using equation (3.4), we collect all the terms with the same order of
are constantsStep 3: The homogeneous balance technique can be used, to determine the positive integer m, between the highest order derivatives and the nonlinear terms appearing in (3.2). After the substitution of (3.3) into (3.2) and using equation (3.4), we collect all the terms with the same order of 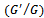 together. Equate each coefficient of the obtained polynomial to zero, yields the set of algebraic equations for K, L, M, λ μ and αi (i = 0, ±1, ±2,…, ± m).Step 4: After solving the system of algebraic equations, and using the equation (3.4), the variety of travelling wave solutions can be obtained using the generalized solutions of equation (3.4).
together. Equate each coefficient of the obtained polynomial to zero, yields the set of algebraic equations for K, L, M, λ μ and αi (i = 0, ±1, ±2,…, ± m).Step 4: After solving the system of algebraic equations, and using the equation (3.4), the variety of travelling wave solutions can be obtained using the generalized solutions of equation (3.4).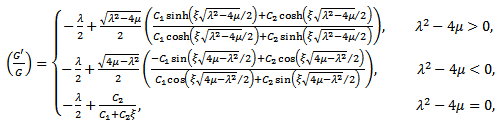 | (3.5) |
where C1 and C2 are arbitrary constants.
4. Fractional Order Coupled Burgers’ Equations
In this section, the improved 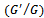 -expansion method has been used to construct the new travelling wave solutions for nonlinear space-time fractional coupled Burgers’ equations (1.1). For this, the following fractional complex transformation
-expansion method has been used to construct the new travelling wave solutions for nonlinear space-time fractional coupled Burgers’ equations (1.1). For this, the following fractional complex transformation where K and L are constants, permits to reduce the equation (1.1) into an ODE. After integrating once, we have the following form:
where K and L are constants, permits to reduce the equation (1.1) into an ODE. After integrating once, we have the following form: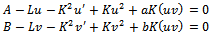 | (4.1) |
Suppose that the solutions of above set of equations can be expressed by 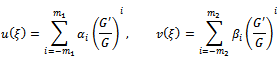 Now by calculating the homogeneous balance (i.e.,
Now by calculating the homogeneous balance (i.e., 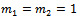 ), between the highest order derivatives and nonlinear term presented in the above equations (4.1), we have the following form
), between the highest order derivatives and nonlinear term presented in the above equations (4.1), we have the following form 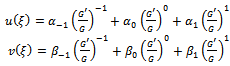 | (4.2) |
where 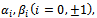 K and L are arbitrary constants. To determine these constants substitute these values into the equations (4.1), and by collecting all the terms with the same power of
K and L are arbitrary constants. To determine these constants substitute these values into the equations (4.1), and by collecting all the terms with the same power of 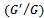 together. Equate each coefficient equal to zero; this yields a set of following algebraic equations:
together. Equate each coefficient equal to zero; this yields a set of following algebraic equations: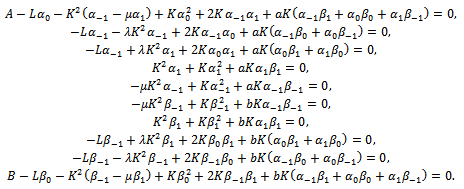 After solving these algebraic equations with the help of software Maple, yields the following three families for the values of
After solving these algebraic equations with the help of software Maple, yields the following three families for the values of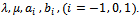 ).Case 1:
).Case 1: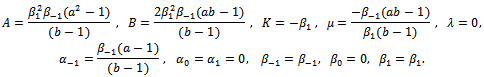 Where
Where 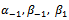 and
and 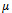 are arbitrary constants with
are arbitrary constants with 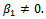 Case 2:
Case 2: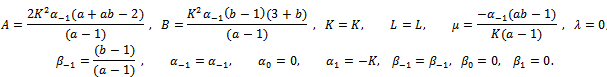 Where and
Where and 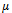 are arbitrary constants.Case 3:
are arbitrary constants.Case 3: 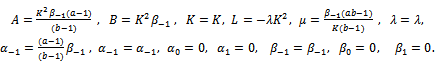 Where
Where 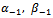 and
and 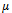 are arbitrary constants.Substituting the above results into the set of equations (4.2) and combining with the equations (3.5), the new series of travelling wave solutions to the equation (1.1) can be celebrated. From Case 1, the following travelling wave solutions can be obtained.When
are arbitrary constants.Substituting the above results into the set of equations (4.2) and combining with the equations (3.5), the new series of travelling wave solutions to the equation (1.1) can be celebrated. From Case 1, the following travelling wave solutions can be obtained.When 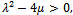 we have
we have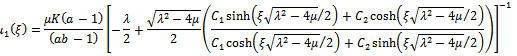 and
and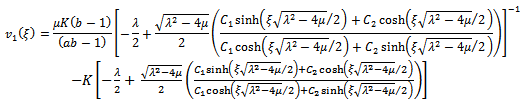 | (4.3) |
where 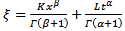 .When
.When 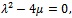 we have the solutions of the form
we have the solutions of the form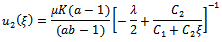 and
and 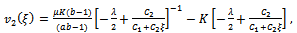 | (4.4) |
with 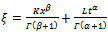 .When
.When 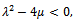 we have the solutions of the form
we have the solutions of the form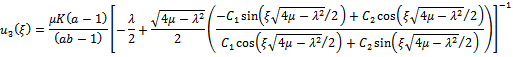 and
and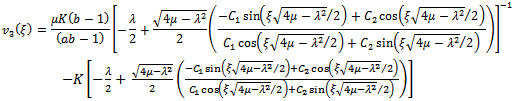 | (4.5) |
where 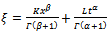 .Especially, if we take
.Especially, if we take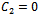 , in equations (4.3), then the following solutions can be obtained.
, in equations (4.3), then the following solutions can be obtained.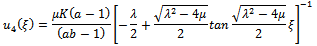 and
and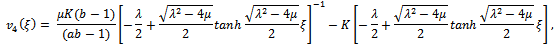 And if we take
And if we take 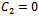 , in equations (4.5), then the following solutions can be obtained.
, in equations (4.5), then the following solutions can be obtained.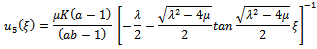 and
and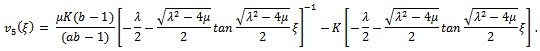 Similarly, as the solutions have been established for case 1, we can construct the corresponding travelling wave solutions from cases 2 and 3.
Similarly, as the solutions have been established for case 1, we can construct the corresponding travelling wave solutions from cases 2 and 3.
5. Conclusions
The extended 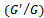 -expansion method has been applied to solve the fractional partial differential equation. As an application, a series of new travelling wave solutions for the space-time fractional order coupled Burgers’ equations have been successfully found. It may be observed that, the nonlinear fractional complex transformation ensures that a certain fractional order differential equations can be turned into ordinary differential equations of integer order. Afterwards, the obtained ODEs can be expressed by a polynomial in
-expansion method has been applied to solve the fractional partial differential equation. As an application, a series of new travelling wave solutions for the space-time fractional order coupled Burgers’ equations have been successfully found. It may be observed that, the nonlinear fractional complex transformation ensures that a certain fractional order differential equations can be turned into ordinary differential equations of integer order. Afterwards, the obtained ODEs can be expressed by a polynomial in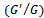 , from where its solution can be obtained using the second order equation
, from where its solution can be obtained using the second order equation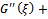
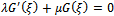 . Since, the homogeneous balancing principle has been used, so we can claim that this method can be applied to other fractional order partial differential equations where the homogeneous balancing principle is satisfied.
. Since, the homogeneous balancing principle has been used, so we can claim that this method can be applied to other fractional order partial differential equations where the homogeneous balancing principle is satisfied.
References
| [1] | J. Zhao, B. Tang, S. Kumar, and Y. Hou, The Extended Fractional Subequation Method for Nonlinear Fractional Differential Equations, Mathematical Problems in Engineering, Vol. 2012, Article ID 924956, 11 pages. |
| [2] | J. H. He, S. K. Elagan, and Z. B. Li, “Geometrical explanation of the fractional complex transform and derivative chain rule for fractional calculus,” Physics Letters. A, vol. 376, no. 4, pp. 257–259, 2012. |
| [3] | Z.-B. Li, J.-H. He, Fractional complex transform for fractional differential equations, Math. Comput. Applications 15(5) (2010) 970-973. |
| [4] | G. Jumarie, Modified Riemann-Liouville derivative and fractional Taylor series of nondifferentiable functions further results, Comput. Math. Appl. 51 (2006) 1367-1624. |
| [5] | I. Podlubny, Fractional Differential Equations, Academic Press, San Diego, 1999. |
| [6] | M. Wang, X. Li, J. Zhang, The 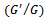 -expansion method and travelling wave solutions of nonlinear evolution equations in mathematical physics, Phys. Lett. A 372 (2008) 417-423. -expansion method and travelling wave solutions of nonlinear evolution equations in mathematical physics, Phys. Lett. A 372 (2008) 417-423. |
| [7] | Q. Wang, Numerical solutions for fractional KDV-Burgers equation by Adomian decomposition method, Appl. Math. Comput. 182 (2006) 1048-1055. |
| [8] | J. Liu, G. Hou, Numerical solutions of the space- and time-fractional coupled Burgers equations by generalized differential transform method, Appl. Math. Comput. 217 (2011) 7001-7008. |
| [9] | Z. Bin, 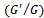 -expansion method for solving fractional partial differential equations in the theory of mathematical physics, Commun. Theory. Phys. 58 (2012) 623-630. -expansion method for solving fractional partial differential equations in the theory of mathematical physics, Commun. Theory. Phys. 58 (2012) 623-630. |
| [10] | S.K. Liu, Z.T. Fu, S.D. Liu, Q. Zhao, Jacobi elliptic function expansion method and periodic wave solutions of nonlinear wave equations, Phys Lett A, 289 (2001) 69-74. |
| [11] | E.J. Parkes, B.R. Duffy, An automated tanh-function method for finding solitary wave solutions to non-linear evolution equations, Comput Phys Comm, 98 (1996) 288-300. |
| [12] | K.A. Gepreel, The homotopy perturbation method applied to the nonlinear fractional Kolmogorov Petrovskii Piskunov equations, Appl. Math. Lett. 24(8) (2011) 1428-1434. |
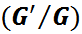 -Expansion Method
-Expansion Method
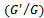 -expansion method has been implemented to find the new travelling wave solutions of nonlinear evolution equations of fractional order. For this, the fractional complex transformation method has been used to convert fractional order partial differential equation to ordinary differential equation. Then,
-expansion method has been implemented to find the new travelling wave solutions of nonlinear evolution equations of fractional order. For this, the fractional complex transformation method has been used to convert fractional order partial differential equation to ordinary differential equation. Then, 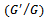 -expansion method has been implemented to celebrate the series of new travelling wave solutions to fractional order coupled Burgers’ equations.
-expansion method has been implemented to celebrate the series of new travelling wave solutions to fractional order coupled Burgers’ equations.
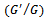 -Expansion Method, Fractional Calculus, Nonlinear Coupled Burgers’ Equations
-Expansion Method, Fractional Calculus, Nonlinear Coupled Burgers’ Equations
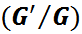 -Expansion Method, American Journal of Computational and Applied Mathematics , Vol. 3 No. 2, 2013, pp. 81-85. doi: 10.5923/j.ajcam.20130302.04.
-Expansion Method, American Journal of Computational and Applied Mathematics , Vol. 3 No. 2, 2013, pp. 81-85. doi: 10.5923/j.ajcam.20130302.04.
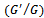 expansion method was introduced, by Wang et al.[6], to find the travelling wave solutions of nonlinear evolution equations. This method was further extended[9] to find the solutions of fractional order differential equations. The Jacobi elliptic function expansion method[10], the tanh-function method for finding solitary wave solutions[11], the homotopy perturbation method[12] have been applied to handle the nonlinear evolution equations etc.In this article, a new approach has been used to find the series of travelling wave solutions to nonlinear evolution equations of fractional order using the fractional complex transformation[3] and the
expansion method was introduced, by Wang et al.[6], to find the travelling wave solutions of nonlinear evolution equations. This method was further extended[9] to find the solutions of fractional order differential equations. The Jacobi elliptic function expansion method[10], the tanh-function method for finding solitary wave solutions[11], the homotopy perturbation method[12] have been applied to handle the nonlinear evolution equations etc.In this article, a new approach has been used to find the series of travelling wave solutions to nonlinear evolution equations of fractional order using the fractional complex transformation[3] and the 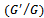 -expansion method[6], in the sense of Jumarie’s modified Riemann-Liouville derivative. For this, we first use the fractional complex transformation to convert into ordinary differential equations. Then, the obtained ODE has been converted into
-expansion method[6], in the sense of Jumarie’s modified Riemann-Liouville derivative. For this, we first use the fractional complex transformation to convert into ordinary differential equations. Then, the obtained ODE has been converted into 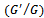 polynomial form. Using the homogenous balance and second order linear ordinary differential equation
polynomial form. Using the homogenous balance and second order linear ordinary differential equation 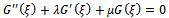 with the aid of computation, the new travelling wave solutions of
with the aid of computation, the new travelling wave solutions of 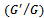 polynomial form has been calculated. As application the nonlinear coupled Burgers’ equations[6] with time-space fractional derivatives has been considered, which has the following form:
polynomial form has been calculated. As application the nonlinear coupled Burgers’ equations[6] with time-space fractional derivatives has been considered, which has the following form: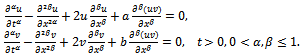
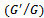 -expansion method has been proposed to find the new travelling wave solutions for NPDEs of fractional order with the help of fractional complex transformation. As an application, the new travelling wave solutions of nonlinear coupled Burgers’ equations have been discussed in section 4. In the last section 5, the conclusion has been drawn.
-expansion method has been proposed to find the new travelling wave solutions for NPDEs of fractional order with the help of fractional complex transformation. As an application, the new travelling wave solutions of nonlinear coupled Burgers’ equations have been discussed in section 4. In the last section 5, the conclusion has been drawn.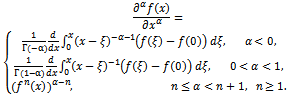
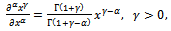
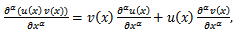
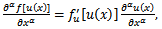
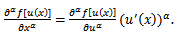
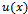 is said to be non-differentiable in equations (2.3) and (2.4) and it is differentiable in (2.5). The function
is said to be non-differentiable in equations (2.3) and (2.4) and it is differentiable in (2.5). The function 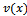 is non-differentiable, and
is non-differentiable, and 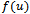 is differentiable in (2.4) and non-differentiable in (2.5). Thus, the formulas (2.3)–(2.5) should be used carefully.In view of[2, 3], the fractional complex transformation can be defined as follows:
is differentiable in (2.4) and non-differentiable in (2.5). Thus, the formulas (2.3)–(2.5) should be used carefully.In view of[2, 3], the fractional complex transformation can be defined as follows: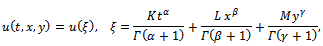 It helps to convert the partial differential equation of fractional order into an ordinary differential equation in very simple and easy manner (where K, L and M are non-zero arbitrary constants). In the following section, the
It helps to convert the partial differential equation of fractional order into an ordinary differential equation in very simple and easy manner (where K, L and M are non-zero arbitrary constants). In the following section, the 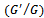 -expansion method has been described to find the travelling wave solutions.
-expansion method has been described to find the travelling wave solutions. 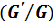 -Expansion Method
-Expansion Method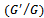 -expansion method[6], can be performed using the following steps. For this, we consider the following NPDE (nonlinear partial differential equation) of fractional order
-expansion method[6], can be performed using the following steps. For this, we consider the following NPDE (nonlinear partial differential equation) of fractional order 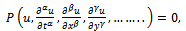
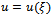 in the following form
in the following form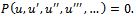
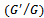 in the form:
in the form: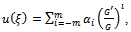
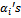 are constants and satisfies the following second order linear ordinary differential equation
are constants and satisfies the following second order linear ordinary differential equation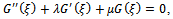
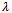 and
and 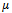 are constantsStep 3: The homogeneous balance technique can be used, to determine the positive integer m, between the highest order derivatives and the nonlinear terms appearing in (3.2). After the substitution of (3.3) into (3.2) and using equation (3.4), we collect all the terms with the same order of
are constantsStep 3: The homogeneous balance technique can be used, to determine the positive integer m, between the highest order derivatives and the nonlinear terms appearing in (3.2). After the substitution of (3.3) into (3.2) and using equation (3.4), we collect all the terms with the same order of 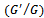 together. Equate each coefficient of the obtained polynomial to zero, yields the set of algebraic equations for K, L, M, λ μ and αi (i = 0, ±1, ±2,…, ± m).Step 4: After solving the system of algebraic equations, and using the equation (3.4), the variety of travelling wave solutions can be obtained using the generalized solutions of equation (3.4).
together. Equate each coefficient of the obtained polynomial to zero, yields the set of algebraic equations for K, L, M, λ μ and αi (i = 0, ±1, ±2,…, ± m).Step 4: After solving the system of algebraic equations, and using the equation (3.4), the variety of travelling wave solutions can be obtained using the generalized solutions of equation (3.4).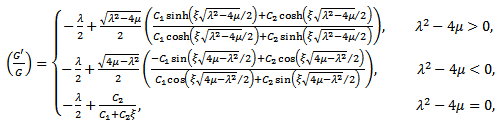
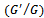 -expansion method has been used to construct the new travelling wave solutions for nonlinear space-time fractional coupled Burgers’ equations (1.1). For this, the following fractional complex transformation
-expansion method has been used to construct the new travelling wave solutions for nonlinear space-time fractional coupled Burgers’ equations (1.1). For this, the following fractional complex transformation where K and L are constants, permits to reduce the equation (1.1) into an ODE. After integrating once, we have the following form:
where K and L are constants, permits to reduce the equation (1.1) into an ODE. After integrating once, we have the following form: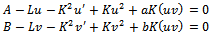
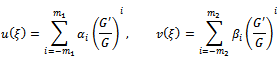 Now by calculating the homogeneous balance (i.e.,
Now by calculating the homogeneous balance (i.e., 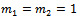 ), between the highest order derivatives and nonlinear term presented in the above equations (4.1), we have the following form
), between the highest order derivatives and nonlinear term presented in the above equations (4.1), we have the following form 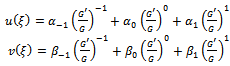
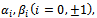 K and L are arbitrary constants. To determine these constants substitute these values into the equations (4.1), and by collecting all the terms with the same power of
K and L are arbitrary constants. To determine these constants substitute these values into the equations (4.1), and by collecting all the terms with the same power of 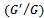 together. Equate each coefficient equal to zero; this yields a set of following algebraic equations:
together. Equate each coefficient equal to zero; this yields a set of following algebraic equations: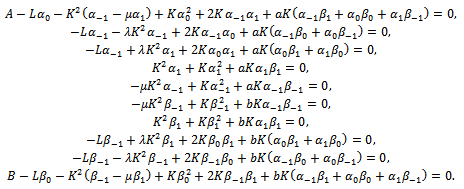 After solving these algebraic equations with the help of software Maple, yields the following three families for the values of
After solving these algebraic equations with the help of software Maple, yields the following three families for the values of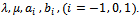 ).Case 1:
).Case 1: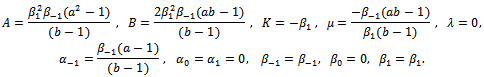 Where
Where 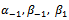 and
and 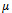 are arbitrary constants with
are arbitrary constants with 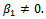 Case 2:
Case 2: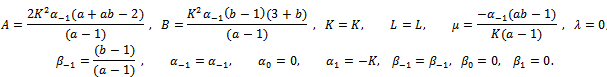 Where and
Where and 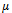 are arbitrary constants.Case 3:
are arbitrary constants.Case 3: 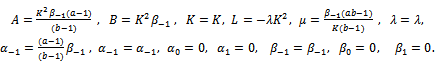 Where
Where 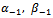 and
and 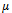 are arbitrary constants.Substituting the above results into the set of equations (4.2) and combining with the equations (3.5), the new series of travelling wave solutions to the equation (1.1) can be celebrated. From Case 1, the following travelling wave solutions can be obtained.When
are arbitrary constants.Substituting the above results into the set of equations (4.2) and combining with the equations (3.5), the new series of travelling wave solutions to the equation (1.1) can be celebrated. From Case 1, the following travelling wave solutions can be obtained.When 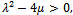 we have
we have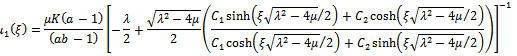 and
and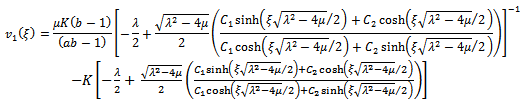
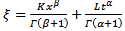 .When
.When 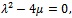 we have the solutions of the form
we have the solutions of the form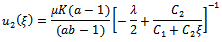 and
and 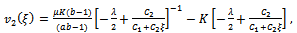
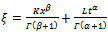 .When
.When 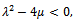 we have the solutions of the form
we have the solutions of the form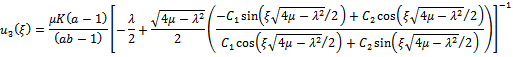 and
and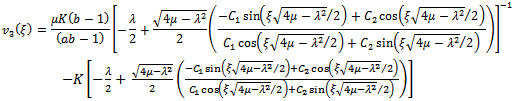
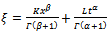 .Especially, if we take
.Especially, if we take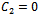 , in equations (4.3), then the following solutions can be obtained.
, in equations (4.3), then the following solutions can be obtained.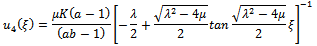 and
and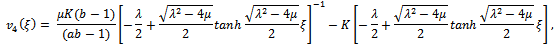 And if we take
And if we take 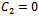 , in equations (4.5), then the following solutions can be obtained.
, in equations (4.5), then the following solutions can be obtained.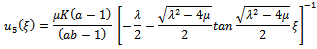 and
and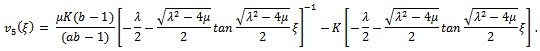 Similarly, as the solutions have been established for case 1, we can construct the corresponding travelling wave solutions from cases 2 and 3.
Similarly, as the solutions have been established for case 1, we can construct the corresponding travelling wave solutions from cases 2 and 3.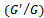 -expansion method has been applied to solve the fractional partial differential equation. As an application, a series of new travelling wave solutions for the space-time fractional order coupled Burgers’ equations have been successfully found. It may be observed that, the nonlinear fractional complex transformation ensures that a certain fractional order differential equations can be turned into ordinary differential equations of integer order. Afterwards, the obtained ODEs can be expressed by a polynomial in
-expansion method has been applied to solve the fractional partial differential equation. As an application, a series of new travelling wave solutions for the space-time fractional order coupled Burgers’ equations have been successfully found. It may be observed that, the nonlinear fractional complex transformation ensures that a certain fractional order differential equations can be turned into ordinary differential equations of integer order. Afterwards, the obtained ODEs can be expressed by a polynomial in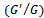 , from where its solution can be obtained using the second order equation
, from where its solution can be obtained using the second order equation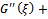
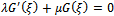 . Since, the homogeneous balancing principle has been used, so we can claim that this method can be applied to other fractional order partial differential equations where the homogeneous balancing principle is satisfied.
. Since, the homogeneous balancing principle has been used, so we can claim that this method can be applied to other fractional order partial differential equations where the homogeneous balancing principle is satisfied. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML -expansion method and travelling wave solutions of nonlinear evolution equations in mathematical physics, Phys. Lett. A 372 (2008) 417-423.
-expansion method and travelling wave solutions of nonlinear evolution equations in mathematical physics, Phys. Lett. A 372 (2008) 417-423.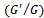 -expansion method for solving fractional partial differential equations in the theory of mathematical physics, Commun. Theory. Phys. 58 (2012) 623-630.
-expansion method for solving fractional partial differential equations in the theory of mathematical physics, Commun. Theory. Phys. 58 (2012) 623-630.