-
Paper Information
- Next Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Computational and Applied Mathematics
p-ISSN: 2165-8935 e-ISSN: 2165-8943
2013; 3(2): 74-80
doi:10.5923/j.ajcam.20130302.03
Magnetohydrodynamic Mixed Convection Flow Past a Wedge Under Variable Temperature and Chemical Reaction
Rudra Kanta Deka1, Sarat Sharma2
1Mathematics Department, Gauhati University, Guwahati, 7840014, India
2Department of Mathematical Sciences, Chaiduar College, Gohpur, 784168, India
Correspondence to: Sarat Sharma, Department of Mathematical Sciences, Chaiduar College, Gohpur, 784168, India.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Steady laminar boundary layer free-forced flow of a Newtonian fluid past a wedge shaped surface is studied. The temperature of the wedge surface is assumed to vary as 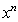 and a first order chemical reaction of the fluid species is considered. The governing boundary layer equations are transformed by the Falknar-Skan transformations and proportionate numerical results are tabulated for the Skin friction, Nusselt number and Sherwood number. Graphical results for the variation in the velocity, temperature and concentration profiles for various values of the temperature exponent, chemical reaction parameter and Schmidt number are presented.
and a first order chemical reaction of the fluid species is considered. The governing boundary layer equations are transformed by the Falknar-Skan transformations and proportionate numerical results are tabulated for the Skin friction, Nusselt number and Sherwood number. Graphical results for the variation in the velocity, temperature and concentration profiles for various values of the temperature exponent, chemical reaction parameter and Schmidt number are presented.
Keywords: MHD, Wedge, Mixed Convection, Chemical Reaction
Cite this paper: Rudra Kanta Deka, Sarat Sharma, Magnetohydrodynamic Mixed Convection Flow Past a Wedge Under Variable Temperature and Chemical Reaction, American Journal of Computational and Applied Mathematics , Vol. 3 No. 2, 2013, pp. 74-80. doi: 10.5923/j.ajcam.20130302.03.
Article Outline
1. Introduction
- Boundary layer flow over a heated vertical surface emerges in a variety of engineering applications and it has been the subject of extensive research. When the fluid is electrically conducting and also exposed to a magnetic field, flow and temperature fields are governed both by the buoyancy and the Lorenz forces. Most of the studies concerning such flows were taken up as steady flows and are considered either for purely free convection or purely forced convection regime only. In dealing with forced convection flow, it is customary to ignore the effects of free convection. Similarly we assume the forced convection as negligible while dealing with free convection flow. The error involved in ignoring natural convection while studying forced convection is negligible at high velocities but may be considerable at low velocities. Situations may arise for which free and forced convection effects are comparable, in which case it is inappropriate to neglect either process. Therefore it is desirable to have a criterion to assess the relative magnitude of natural convection in the presence of forced convection flows. Such flows situations where both free and forced convection effects are of comparable order belong to the mixed convection regime. In several practical applications of heat transfer theory to the vertical plate problems there exists significant temperature difference between the surface of the hot plate and the free stream. This temperature difference cause density gradients in the fluid medium and in the presence of a gravitational body force, free convection effects become important. It has generally been recognized that,
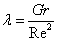 where Gr is the Grashof number and Re the Reynolds number is the governing parameter for the laminar boundary layer forced-free mixed convection flow which represents the ratio of the buoyancy forces to the inertial forces inside the boundary layer. Forced convection exists when
where Gr is the Grashof number and Re the Reynolds number is the governing parameter for the laminar boundary layer forced-free mixed convection flow which represents the ratio of the buoyancy forces to the inertial forces inside the boundary layer. Forced convection exists when 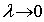 which occurs at the leading edge and the free convection limit can be reached if
which occurs at the leading edge and the free convection limit can be reached if 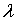 becomes large. We know from authoritative work in heat transfer[1] that free convection is negligible if
becomes large. We know from authoritative work in heat transfer[1] that free convection is negligible if 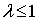 and forced convection is negligible if
and forced convection is negligible if 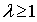 . Hence combined free and forced (or mixed) convection regime is generally one for which
. Hence combined free and forced (or mixed) convection regime is generally one for which 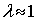 . Although the flows with only one of the two effects involved will have a self similar character, such situations will mathematically lead to ordinary differential equations and are easy to solve. But as soon as the two effects occur together, boundary value problem involving partial differential equations will arise and are not easy to solve by conventional procedures. The physical explanation of the complexities is that the two effects act differently with respect to the characteristic length l and any combination means that the characteristic length is introduced into the problem (i.e., the length from the leading edge to the separation position).If both the effects are to be considered, pure forced convection always dominates for l→0 while direct natural convection dominates for l→∞. Most of the works concerning external flows past a vertical surface are taken up as steady flows and they are either considered for free or forced convection regimes only. However free-forced or popularly known as mixed convection flows received considerable attention in the late 1970s to 1980s and numerous literature reviews are available. Soundalgekar et al[2] studied the flow past a semi-infinite vertical plate under variable temperature. Wilks[3] and Raju et al[4] have shown several formulations under which a flow can be classified as belonging to the mixed convection regime and values of the mixed convection parameters were used by them. In nature it is rather impossible to find pure fluid unless special efforts are made to obtain it.The most common fluids like water, air etc. is contaminated with impurities like
. Although the flows with only one of the two effects involved will have a self similar character, such situations will mathematically lead to ordinary differential equations and are easy to solve. But as soon as the two effects occur together, boundary value problem involving partial differential equations will arise and are not easy to solve by conventional procedures. The physical explanation of the complexities is that the two effects act differently with respect to the characteristic length l and any combination means that the characteristic length is introduced into the problem (i.e., the length from the leading edge to the separation position).If both the effects are to be considered, pure forced convection always dominates for l→0 while direct natural convection dominates for l→∞. Most of the works concerning external flows past a vertical surface are taken up as steady flows and they are either considered for free or forced convection regimes only. However free-forced or popularly known as mixed convection flows received considerable attention in the late 1970s to 1980s and numerous literature reviews are available. Soundalgekar et al[2] studied the flow past a semi-infinite vertical plate under variable temperature. Wilks[3] and Raju et al[4] have shown several formulations under which a flow can be classified as belonging to the mixed convection regime and values of the mixed convection parameters were used by them. In nature it is rather impossible to find pure fluid unless special efforts are made to obtain it.The most common fluids like water, air etc. is contaminated with impurities like 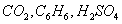 etc. and generally we have to consider presence of such foreign masses while studying flows past different bodies. In such a case the density difference in the fluid is caused by material constitution in addition to temperature differences. The common example of such a flow is the atmospheric flow which is driven appreciably by both temperature and concentration differences. When such contaminant is present in the fluid under consideration there does occur some chemical reaction e.g. air and benzene react chemically, so also water and sulfuric acid. During such chemical reactions, there is always generation of heat. But when the foreign mass present in the fluid at very low level, we can assume a first order chemical reaction and the heat generated due to chemical reaction can be very negligible. Several authors have done significant works by taking into account a first order chemical reaction on flow past vertical surfaces. Das et al[5] studied the effect of mass transfer and chemical reaction on the flow past a vertical plate. Bala[6] considered a porous, moving vertical plate under variable suction and chemical reaction. Mahmoud[7] studied mixed convection flow under variable viscosity and chemical reaction effects. Flow past a wedge or ‘wedge flow’ belongs to a special class of boundary layer flow problems where the shape of the wedge affects the boundary layer mainly by determining the pressure gradient along the surface of the wedge. Flow past a wedge of angle
etc. and generally we have to consider presence of such foreign masses while studying flows past different bodies. In such a case the density difference in the fluid is caused by material constitution in addition to temperature differences. The common example of such a flow is the atmospheric flow which is driven appreciably by both temperature and concentration differences. When such contaminant is present in the fluid under consideration there does occur some chemical reaction e.g. air and benzene react chemically, so also water and sulfuric acid. During such chemical reactions, there is always generation of heat. But when the foreign mass present in the fluid at very low level, we can assume a first order chemical reaction and the heat generated due to chemical reaction can be very negligible. Several authors have done significant works by taking into account a first order chemical reaction on flow past vertical surfaces. Das et al[5] studied the effect of mass transfer and chemical reaction on the flow past a vertical plate. Bala[6] considered a porous, moving vertical plate under variable suction and chemical reaction. Mahmoud[7] studied mixed convection flow under variable viscosity and chemical reaction effects. Flow past a wedge or ‘wedge flow’ belongs to a special class of boundary layer flow problems where the shape of the wedge affects the boundary layer mainly by determining the pressure gradient along the surface of the wedge. Flow past a wedge of angle 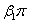 yields a different pressure profile for each value of
yields a different pressure profile for each value of 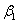 , thereby offering insight into boundary layer behavior in a number of situations. Two of the special cases are planar stagnation flow
, thereby offering insight into boundary layer behavior in a number of situations. Two of the special cases are planar stagnation flow 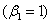 and parallel flow past a flat plate
and parallel flow past a flat plate 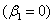 .Martin and Boyd[8] studied the flow past a wedge with slip boundary conditions using Falkner-Skan transformations together with a finite difference method. Mukhopadhyay[9] studied the effect of radiation and variable viscosity on the flow past a wedge using a special form of scaled Lie group of transformations. Nazar and Pop[10] considered the case of a moving wedge using the Falkner-Skan transformations. Ece[11] used the Thomas algorithm to solve the similar boundary layer equations of flow past a wedge under mixed thermal boundary conditions. Hsu et. al.[12] utilized the series expansion method to study the flow of a second grade fluid past a wedge. Massoudi[13], Mureithi and Mason[14], Loganathan et. al.[15] employed the
.Martin and Boyd[8] studied the flow past a wedge with slip boundary conditions using Falkner-Skan transformations together with a finite difference method. Mukhopadhyay[9] studied the effect of radiation and variable viscosity on the flow past a wedge using a special form of scaled Lie group of transformations. Nazar and Pop[10] considered the case of a moving wedge using the Falkner-Skan transformations. Ece[11] used the Thomas algorithm to solve the similar boundary layer equations of flow past a wedge under mixed thermal boundary conditions. Hsu et. al.[12] utilized the series expansion method to study the flow of a second grade fluid past a wedge. Massoudi[13], Mureithi and Mason[14], Loganathan et. al.[15] employed the 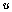 Non-similarity method to solve wedge flow problems. Sattar[16] considered the unsteady flow past a wedge by the Local similarity method. Pop and Watanabe[17], Kandasamy et al.[18], Kandasami et al.[19], Kandasami et al.[20] studied the flow situations past a wedge by introducing a pair of variables
Non-similarity method to solve wedge flow problems. Sattar[16] considered the unsteady flow past a wedge by the Local similarity method. Pop and Watanabe[17], Kandasamy et al.[18], Kandasami et al.[19], Kandasami et al.[20] studied the flow situations past a wedge by introducing a pair of variables 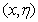 instead of
instead of 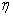 or a dimensionless distance
or a dimensionless distance 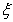 along the plate of the wedge. Williams and Rhyne[21] have used a group of transformations to encompass both the situations of small and large time in the unsteady flow past a wedge by simple modification of the Falkner and Skan transformations in solving the wedge equations employing the Thomas algorithm. Kumari and Nath[22] have successfully implemented these transformations in the study of unsteady flow past a vertical plate and shown their efficacy.Despite numerous solution techniques and transformation methods available for the governing boundary layer equations arising in the flow past a wedge, the Falkner-Skan transformations remains one of the most chosen and used for their simplicity and computational ease. All the above cited works concerning flow past a wedge were carried out by assuming a constant temperature of the wedge surface. Here we propose to undertake this study by adopting the popular Falkner-Skan transformations to solve our problem by considering a variable temperature along the surface of the wedge under a first order chemical reaction. We will also study the variation in velocity, temperature and concentration profiles for various values of Schmidt numbers.
along the plate of the wedge. Williams and Rhyne[21] have used a group of transformations to encompass both the situations of small and large time in the unsteady flow past a wedge by simple modification of the Falkner and Skan transformations in solving the wedge equations employing the Thomas algorithm. Kumari and Nath[22] have successfully implemented these transformations in the study of unsteady flow past a vertical plate and shown their efficacy.Despite numerous solution techniques and transformation methods available for the governing boundary layer equations arising in the flow past a wedge, the Falkner-Skan transformations remains one of the most chosen and used for their simplicity and computational ease. All the above cited works concerning flow past a wedge were carried out by assuming a constant temperature of the wedge surface. Here we propose to undertake this study by adopting the popular Falkner-Skan transformations to solve our problem by considering a variable temperature along the surface of the wedge under a first order chemical reaction. We will also study the variation in velocity, temperature and concentration profiles for various values of Schmidt numbers.2. Formulation of the Problem
- Let us consider the steady two-dimensional hydro magnetic mixed convection boundary layer flow past the surface of a wedge. We formulate the problem in a body fixed rectangular coordinate system in which x is measured along the surface of the wedge, from the apex, and y is measured normal to the wedge surface. The flow configuration is shown in fig1. The fluid is assumed to be Newtonian and its physical property variations due to temperature is limited to density only. A uniform transverse magnetic field of strength
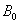 is applied parallel to the y-axis and induced magnetic field is neglected. The concentration of diffusing species is very small in comparison to other chemical species and far from the surface of the wedge the concentration is assumed infinitesimally small and hence the Dufour and Soret effects are neglected. Also there is first order chemical reaction taking place in the flow. Assuming Boussinesq approximation, the boundary layer governing equations of momentum, energy and diffusion for the flow problem are:
is applied parallel to the y-axis and induced magnetic field is neglected. The concentration of diffusing species is very small in comparison to other chemical species and far from the surface of the wedge the concentration is assumed infinitesimally small and hence the Dufour and Soret effects are neglected. Also there is first order chemical reaction taking place in the flow. Assuming Boussinesq approximation, the boundary layer governing equations of momentum, energy and diffusion for the flow problem are: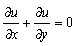 | (1) |
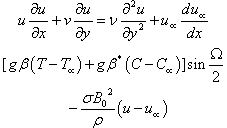 | (2) |
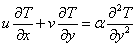 | (3) |
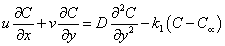 | (4) |
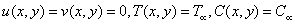 for
for 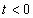 For
For 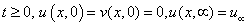
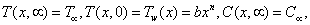
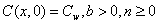 | (5) |
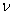 is the kinematic viscosity, g is the acceleration due to gravity,
is the kinematic viscosity, g is the acceleration due to gravity, 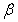 is the volumetric coefficient of thermal expansion,
is the volumetric coefficient of thermal expansion, 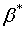 is the volumetric coefficient of concentration,
is the volumetric coefficient of concentration, 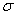 is the electrical conductivity,
is the electrical conductivity, 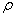 is the density,
is the density, 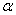 is the thermal diffusivity, D is the effective diffusion coefficient and the subscripts w and ∞ denote conditions at the surface of the wedge and in the free stream respectively.We now introduce the following Falkner-Skan transformations for wedge flow as given in[1] and[23] with
is the thermal diffusivity, D is the effective diffusion coefficient and the subscripts w and ∞ denote conditions at the surface of the wedge and in the free stream respectively.We now introduce the following Falkner-Skan transformations for wedge flow as given in[1] and[23] with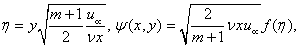
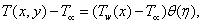
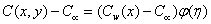 | (6) |
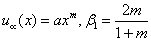 | (7) |
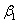 is the Hartree pressure gradient parameter that corresponds to
is the Hartree pressure gradient parameter that corresponds to 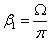 for a total angle
for a total angle 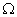 of the wedge. Two important cases are the flat plate flow (m=0) and the stagnation-point flow (m=1). For accelerated flows
of the wedge. Two important cases are the flat plate flow (m=0) and the stagnation-point flow (m=1). For accelerated flows 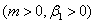 velocity profiles exhibit no point of inflexion but for retarded flows
velocity profiles exhibit no point of inflexion but for retarded flows 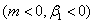 there exists a point of inflexion. The case
there exists a point of inflexion. The case 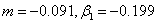 is a limiting case, no solution to the Falkner-Skan equation for accelerated forward flow exist for
is a limiting case, no solution to the Falkner-Skan equation for accelerated forward flow exist for 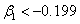 which corresponds to the velocity profile with vanishing wall shear stress (separation). Numerical results from Hartree are plotted for various wedge angles in[1].The velocity components are given in terms of the stream function
which corresponds to the velocity profile with vanishing wall shear stress (separation). Numerical results from Hartree are plotted for various wedge angles in[1].The velocity components are given in terms of the stream function  by the relations:
by the relations: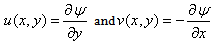 | (8) |
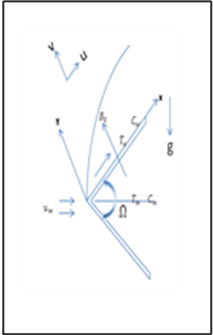 | Figure 1. Flow Configuration |
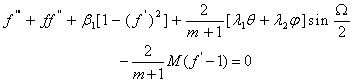 | (9) |
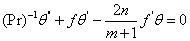 | (10) |
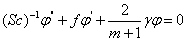 | (11) |
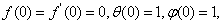
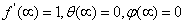 | (12) |
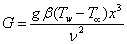 is the thermal Grashof number,
is the thermal Grashof number, 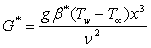 is the species Grashof number,
is the species Grashof number, 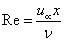 is the Reynolds number,
is the Reynolds number, 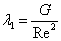 is the buoyancy parameter due to temperature,
is the buoyancy parameter due to temperature, 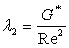 is the buoyancy parameter due to mass,
is the buoyancy parameter due to mass, 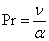 is the Prandtl number,
is the Prandtl number, 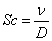 is the Schmidt number,
is the Schmidt number, 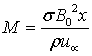 is the magnetic parameter and
is the magnetic parameter and 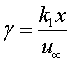 is the chemical reaction parameter. Here η is the transformed similarity variable, ψ is the dimensional and f(η) is the dimensionless stream function, θ(η) is the dimensionless temperature, φ(η) is the dimensionless concentration and primes denote differentiation with respect to η.Knowing the velocity field, the physical quantities of interest to our study are the Skin friction
is the chemical reaction parameter. Here η is the transformed similarity variable, ψ is the dimensional and f(η) is the dimensionless stream function, θ(η) is the dimensionless temperature, φ(η) is the dimensionless concentration and primes denote differentiation with respect to η.Knowing the velocity field, the physical quantities of interest to our study are the Skin friction 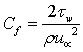 which is given by the wall shear stress
which is given by the wall shear stress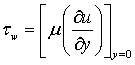 , the Local Nusselt number
, the Local Nusselt number 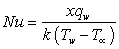 given by the heat flux
given by the heat flux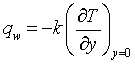 and the Local Sherwood number
and the Local Sherwood number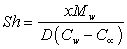 given by the mass flux
given by the mass flux 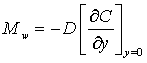 .In view of (12), the Skin Friction coefficient
.In view of (12), the Skin Friction coefficient 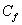 reduces to
reduces to 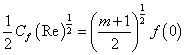 | (13) |
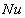 reduces to
reduces to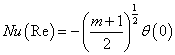 | (14) |
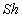 reduces to
reduces to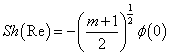 | (15) |
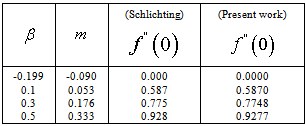
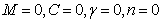 in our code which are in excellent agreement (Table1).
in our code which are in excellent agreement (Table1).
|
3. Numerical Solution
- We propose to solve equations (9) – (11) under the boundary conditions (12) using the continuation method with the help of Matlab7 which implements a finite difference code. Continuation method is an improved shooting method which reduces the chance of carrying on the computational errors due to poor guesses of the unknown values and ensures greater accuracy. In continuation method firstly we find the unknown boundary conditions for
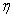 =1 for a guess and put those values for
=1 for a guess and put those values for 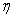 =2 and carry on the process until the values converge to fixed values. Finally the converged initial values are put as the initial values in solving the boundary value problem for the entire range
=2 and carry on the process until the values converge to fixed values. Finally the converged initial values are put as the initial values in solving the boundary value problem for the entire range 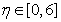 .We have tabulated the values in Table2-Table5 of
.We have tabulated the values in Table2-Table5 of 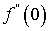 ,
, 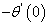 and
and 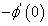 which are proportional to the Skin friction, Nusselt number and Sherwood number respectively under magnetic, plate temperature variation, chemical reaction and Schmidt number variation. We have kept other parameters as constant while analyzing the effects of one parameter which will highlight the changes (if any) more clearly. The velocity, temperature and concentration profiles are presented in Figure2-Figure5.
which are proportional to the Skin friction, Nusselt number and Sherwood number respectively under magnetic, plate temperature variation, chemical reaction and Schmidt number variation. We have kept other parameters as constant while analyzing the effects of one parameter which will highlight the changes (if any) more clearly. The velocity, temperature and concentration profiles are presented in Figure2-Figure5.
|
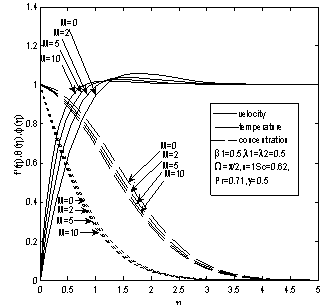 | Figure 2. Magnetic effect on velocity, temperature and concentration profile |
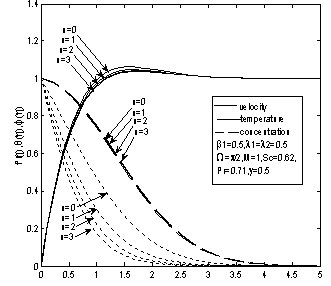 | Figure 3. Effect of variable temperature on velocity, temperature and concentration profile |
|
|
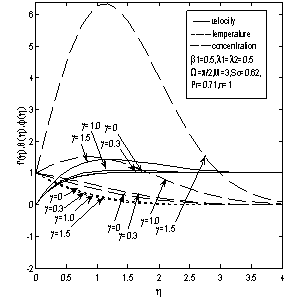 | Figure 4. Effect of chemical reaction on velocity, temperature and concentration profile |
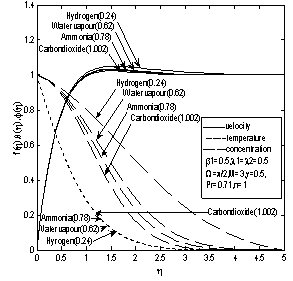 | Figure 5. Effect of Schmidt number on velocity, temperature and concentration profile |
 for different values of
for different values of 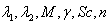 (Table2), for which separation of flow occurs. The result shows that flow separation can effectively be controlled by introduction of magnetic, chemical reaction and plate temperature variation effects into the flow field.
(Table2), for which separation of flow occurs. The result shows that flow separation can effectively be controlled by introduction of magnetic, chemical reaction and plate temperature variation effects into the flow field.4. Results and Discussion
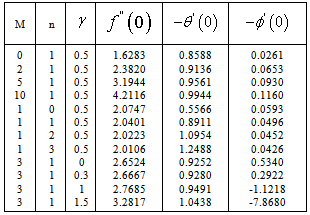
- In our effort to analyze the effects of transverse magnetic field on the velocity, temperature and concentration profiles, we have fixed the values of the plate temperature exponent at 1 and the chemical reaction parameter at 0.5. The values of
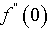 ,
, 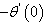 and
and 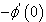 are tabulated in Table3. The velocity, temperature and concentration profiles for the flow are presented Figure2. It is seen from Figure2 that magnetic field induces considerable influence on the flow field. Increasing magnetic field strength has a enhancing effect on the velocity of the fluid under consideration. Magnetic field tends to decrease the temperature and concentration at equal proportion for the flow. In Table3, values of skin friction, rate of heat flux and rate of mass flux show a increasing trend with the increase of magnetic field strength. Effects of variation in the plate temperature upon the velocity, temperature and concentration of the fluid is computed by keeping the magnetic field strength as 1 and chemical reaction parameter as 0.5. The values of
are tabulated in Table3. The velocity, temperature and concentration profiles for the flow are presented Figure2. It is seen from Figure2 that magnetic field induces considerable influence on the flow field. Increasing magnetic field strength has a enhancing effect on the velocity of the fluid under consideration. Magnetic field tends to decrease the temperature and concentration at equal proportion for the flow. In Table3, values of skin friction, rate of heat flux and rate of mass flux show a increasing trend with the increase of magnetic field strength. Effects of variation in the plate temperature upon the velocity, temperature and concentration of the fluid is computed by keeping the magnetic field strength as 1 and chemical reaction parameter as 0.5. The values of 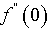 ,
, 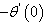 and
and 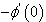 are tabulated in Table3. The velocity and temperature profiles for the flow are presented for comparison in Figure3. For constant plate temperature the velocity of the flow is at a high level. But as we increase the plate temperature exponent the velocity becomes lesser gradually. For temperature, there is a uniform lowering effect for the flow with the increase of plate temperature but for concentration the change though minimally lowering, is not significant. From Table3, it is seen that increase in plate temperature reduces the skin friction and mass flux of the flow but heat flux increases. To study the chemical reaction effects we have taken the magnetic field strength as 3 and the plate temperature exponent as 1. The values of
are tabulated in Table3. The velocity and temperature profiles for the flow are presented for comparison in Figure3. For constant plate temperature the velocity of the flow is at a high level. But as we increase the plate temperature exponent the velocity becomes lesser gradually. For temperature, there is a uniform lowering effect for the flow with the increase of plate temperature but for concentration the change though minimally lowering, is not significant. From Table3, it is seen that increase in plate temperature reduces the skin friction and mass flux of the flow but heat flux increases. To study the chemical reaction effects we have taken the magnetic field strength as 3 and the plate temperature exponent as 1. The values of 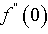 ,
, 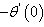 and
and 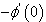 are tabulated in Table3.The velocity, temperature and concentration profiles for flow are presented in Figure4. Presence of a first order chemical reaction at low level increases the velocity and concentration of the fluid but temperature comes down. Table3 shows that in the absence of chemical reaction, the rate of skin friction is comparatively more than the heat and mass flux. For small change in the chemical reaction strength, skin friction and heat flux increases but mass flux decreases. For higher chemical reaction level concentration level increases considerably.Effects of variation in the species of diffusing species in terms of their Schmidt numbers is studied by taking the magnetic field strength as 1, the plate temperature exponent as 1 and for a low level of chemical reaction
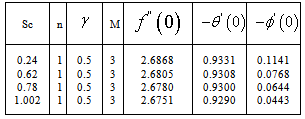
are tabulated in Table3.The velocity, temperature and concentration profiles for flow are presented in Figure4. Presence of a first order chemical reaction at low level increases the velocity and concentration of the fluid but temperature comes down. Table3 shows that in the absence of chemical reaction, the rate of skin friction is comparatively more than the heat and mass flux. For small change in the chemical reaction strength, skin friction and heat flux increases but mass flux decreases. For higher chemical reaction level concentration level increases considerably.Effects of variation in the species of diffusing species in terms of their Schmidt numbers is studied by taking the magnetic field strength as 1, the plate temperature exponent as 1 and for a low level of chemical reaction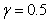 . The values of
. The values of 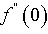 ,
, 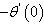 and
and 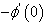 are tabulated in Table4.The velocity, temperature and concentration profiles for flow are presented in Figure5. Lighter diffusing species has a higher velocity and concentration compared to the heavier species. Temperature is not changed with a change in the Schmidt number.Table4 shows that in the presence of nominal chemical reaction, the skin friction, heat flux and mass flux gradually decreases with increase in Schmidt numbers.
are tabulated in Table4.The velocity, temperature and concentration profiles for flow are presented in Figure5. Lighter diffusing species has a higher velocity and concentration compared to the heavier species. Temperature is not changed with a change in the Schmidt number.Table4 shows that in the presence of nominal chemical reaction, the skin friction, heat flux and mass flux gradually decreases with increase in Schmidt numbers.5. Conclusions
- (i) Magnetic field accelerates the velocity and lowers the temperature and concentration.(ii) Skin-friction, heat flux and mass flux increase due to magnetic field.(iii) Increasing plate temperature lowers the velocity and temperature considerably but a minor lowering effect for concentration is found.(iv) Skin-friction and mass flux decrease but heat flux increases with plate temperature.(v) At low level of chemical reaction velocity, temper ature and concentration increase gradually but for higher level the reverse is true.(vi) For low level of chemical reaction skin-friction, heat flux increase but mass flux decreases. For higher level the reverse is true.(vii) For low Schmidt number the velocity and concentration is higher but temperature remains same.(viii) In the presence of nominal chemical reaction the skin-friction, heat flux and mass flux increases with increase in Schmidt number.
6. Nomenclature
- Gr Grashof number,Re Reynolds number,
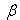 coefficient of thermal expansion ,
coefficient of thermal expansion , 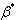 coefficient of thermal expansion with concentration ,
coefficient of thermal expansion with concentration ,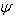 stream function,
stream function,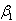 Hartree parameter,G thermal Grashof number,
Hartree parameter,G thermal Grashof number,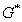 mass Grashof number, magnetic field strength,
mass Grashof number, magnetic field strength,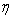 similarity variable,
similarity variable,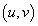 dimension less velocity components,
dimension less velocity components,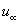 free stream fluid velocity,
free stream fluid velocity,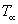 free stream temperature,
free stream temperature,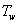 temperature at the plate,M magnetic parameter,
temperature at the plate,M magnetic parameter,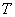 dimensionless temperature,
dimensionless temperature,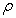 density,
density,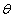 dimensionless temperature,
dimensionless temperature,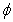 dimensionless species concentration,
dimensionless species concentration,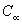 species concentration in the free stream,
species concentration in the free stream,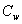 concentration at the wall,g acceleration due to gravity,
concentration at the wall,g acceleration due to gravity,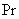 Prandtl number,
Prandtl number,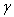 chemical reaction parameter,
chemical reaction parameter, Schmidt number,
Schmidt number,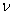 kinematic viscosity,
kinematic viscosity,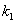 chemical reaction constant,
chemical reaction constant,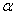 thermal diffusivity,
thermal diffusivity,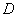 mass diffusion coefficient,n temperature exponent
mass diffusion coefficient,n temperature exponent Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML