Arun Kumar Gupta1, Harvinder Kaur2
1Department of Mathematics, M.S.College, Saharanpur-247001, U.P., India
2Department of Mathematics, Govt.P.G. College, Sec 1, Panchkula, Haryana , India
Correspondence to: Arun Kumar Gupta, Department of Mathematics, M.S.College, Saharanpur-247001, U.P., India.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
The mainstream of visco- elastic materials are receptive to heat and in space technology, highly speed space flights, internal combustion engines, satellites, certain parts of mechanical structures have to man oeuvre under elevated temperatures consequently the state of affairs are thermal sensitive. It is observed that thermal effects are recurrently overlooked in most of the cases so far they have to be taken in to concern. It is significant to study vibration behaviour in the presence of thermal gradient due to rising use of modern materials in structural components. Moreover, weight of composite structure is minimized by optimizing its lay up and by tapering its thickness. This paper is the study of thermal effect on free transverse vibrations of clamped rectangular plate. The plate is considered to be varying in thickness as exponentially in both directions. Rayleigh-Ritz technique is applied to give a good approximation for the frequency corresponding to the first two modes of vibration. A two terms deflection function has been used as a solution. The effect of linear temperature variation has been considered. Deflection and time period corresponding to the first two modes of vibrations of clamped plate have been computed for various values of aspect ratio, thermal constants, and taper constants. Comparison have been done with published one for unheated plate and found in close agreement.
Keywords:
Vibration, Rectangular Plate, Thickness Variation, Rayleigh-Ritz Technique, Visco-Elastic Mechanics, Temperature Gradient
Cite this paper: Arun Kumar Gupta, Harvinder Kaur, Effect of Thermal Gradient on Vibration of Clamped Visco-elastic Rectangular Plate with Exponentially Thickness Variation in Both the Directions, American Journal of Computational and Applied Mathematics, Vol. 3 No. 1, 2013, pp. 36-45. doi: 10.5923/j.ajcam.20130301.07.
1. Introduction
The study of vibrations come up with the oscillatory behaviour of bodies and it is experienced that many technological designed structures experience vibrations therefore the study of vibration of plates of certain aspect ratios with some simple boundary conditions is the call for of the present time. Some new materials also posses time dependent behaviour which is also influential. The requirement of technically better designed filaments and parts of machines in aircraft structures, jet engine, nuclear power plants and building activities in the cold regions has enhanced the constraint of study of various problems of plates continuously supported by elastic or visco-elastic media. As visco-elasticity is the property of many modern materials by nature and visco-elastic plates are recurrently approximated for analytical purpose and for this reason the vibrations of such plates are of great meaningful. In the course of time, the study of vibration of plates has acquired great weight age in the field of research, engineering and space technology. Further, the study of vibration behaviour in the presence of thermal gradient of visco-elastic plates is required due to its practical importance in the field of engineering because Machines very repeatedly operate under diverse temperature conditions. In majority of cases the impact of temperature are ignored yet they need to be taken in to consideration. The reason behind this is that during heated up periods structures are exposed to high intensity heat fluxes and the material properties undergo significant changes hence the thermal effect on modulus of elasticity of material cannot be neglected. Most of engineering materials are found to have linear relationship between modulus of elasticity and temperature. Applications of such materials are due to lessening of weight and size, low operating cost and enhancement in efficiency and strength.Further, tapering saves weight by removing preventable weight. Thickness tapering is advantageous since stresses tend to vary appreciably within the structure.Free vibration of visco-elastic orthotropic rectangular plates was discussed by Sobotka[1]. The effect of a thermal gradient on the frequencies of an orthotropic plate of variable thickness has been discussed by Tomar and Gupta[2]. Singh and Saxena[3] worked on transverse vibration of rectangular plate with bi-directional thickness variation. Gupta and Khanna[4] studied the vibration of visco-elastic rectangular plate with linearly thickness variations in both directions. Li[5] discussed the vibration analysis of rectangular plate with general elastic boundary supports. Gupta et al.[6] solved the problem of vibration of visco elastic parallelogram plate with parabolic thickness variation. Gupta and Kumar[7] studied the effect of thermal gradient on vibration of non-homogeneous visco- elastic elliptic plate of variable thickness. Free vibration analysis of non-homogeneous visco-elastic circular plate with varying thickness subject to thermal gradient was studied by Gupta and Kumar[8]. Recently, Gupta and Sharma[11] studied the thermally induced vibration of non-homogeneous trapezoidal plate with varying thickness and density.This present paper is the study of the thermal effect on vibration of clamped visco-elastic rectangular plate whose thickness varies exponentially in both directions with the assumption that the plate is clamped on all the four edges. A frequency equation of plate has been obtained by Rayleigh-Ritz technique for two terms of deflection function. The assumption of small deflection and linear visco-elastic properties of ‘Kelvin’ type are taken. Time period and deflection at different points for the first two modes of vibration are calculated for various values of thermal gradients, aspect ratio and taper constants. Also results are illustrated with graphs. Here it is important to note that all the numerical calculations have been made using the material constants of ‘Duralium’ an alloy of Aluminium, Copper and traces of Magnesium and Manganese.
2. Formulation of Problem and Equation of Motion
The equation of transverse motion of a visco-elastic plate of variable thickness, taken in Cartesian co-ordinates, density ρ , thickness of plate h, deflection w and time t is given by Bhatnagar and Gupta[10]: 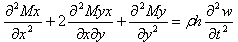 | (1) |
The constitutive relation for Mx, My, Myx are given by: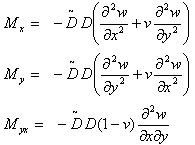 | (2) |
Here 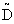 is Rheological operator and
is Rheological operator and 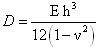 is flexural rigidity, in which ν is the Poisson’s ratio and E is Young modulus of elasticity.Since the thickness of the visco-elastic plate varies in two directions i.e. in x and y direction, consequently thickness h and flexural rigidity of the plate become function of x and y, therefore taking deflection w as a product of two functions as:
is flexural rigidity, in which ν is the Poisson’s ratio and E is Young modulus of elasticity.Since the thickness of the visco-elastic plate varies in two directions i.e. in x and y direction, consequently thickness h and flexural rigidity of the plate become function of x and y, therefore taking deflection w as a product of two functions as: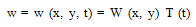 | (3) |
where W (x, y) is the function of coordinates in x, y and T (t) is a time function.Using equation (3) in equations (1) and (2) and then equating both sides of the equation to a constant, say k2, one gets two separate differential equations as follows: 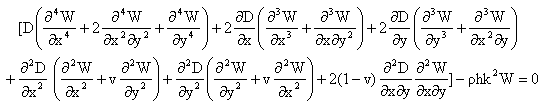 | (4) |
and 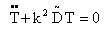 | (5) |
Here dot denotes time derivative.Equation (4) is a differential equation of transverse motion and equation (5) is a differential equation of time function of free vibration of visco-elastic plate of variable thickness.With the assumption that the temperature of the visco-elastic rectangular plate varies linearly in one dimension only i.e. along x-axis and also if τ and τ0 denote the increase in temperatures above the reference temperature at any point at distance x/a and at the end x= 0 respectively then τ can be expressed as: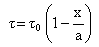 | (6) |
Here a is the length of the plate.The temperature dependence of the modulus of elasticity for most of engineering materials as is given by Tomar and Gupta[2]: is: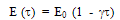 | (7) |
where E0 is the value of Young’s modulus at some reference temperature i.e. τ=0 and γ is the slope of the variation of E with τ.On substituting the value of τ from equation (6) into (7), one gets: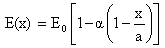 | (8) |
where α = γτ0 (0 < α <1), known as thermal gradient. The expression for Kinetic energy P and Strain energy V as given by Leissa[9] are: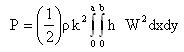 | (9) |
and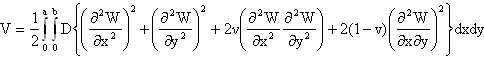 | (10) |
The thickness of the visco-elastic rectangular plate is assumed to vary exponentially in both directions i.e.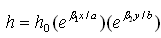 | (11) |
Here b is the width of the plate, β1 and β2 are taper constants along x-axis and y-axis respectively and h0 is the thickness of the plate at x=y=0.
3. Boundary Conditions and Frequency Equation
Here we are using Rayleigh-Ritz technique for finding the solution. This method implies that maximum strain energy must be equal to the maximum kinetic energy; therefore, the problem under consideration must satisfy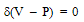 | (12) |
for arbitrary variation of W satisfying relevant geometrical boundary condition.The boundary conditions for a rectangular plate clamped (c) along all the four edges are: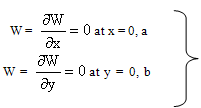 | (13) |
and the corresponding two-term deflection function is taken as: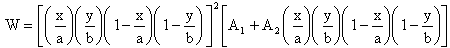 | (14) |
which is satisfied by equation (13).Here A1 and A2 are determined by using equation (13).Assuming the non-dimensional variables as: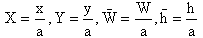 | (15) |
In view of equations (11) and (14), equations (9) and (10), become: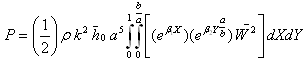 | (16) |
and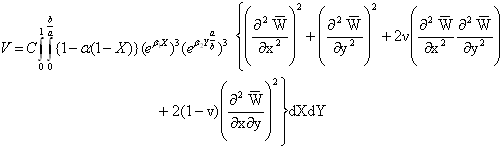 | (17) |
where 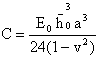 Here variation of X is from 0 to 1 and that of Y is from 0 to b/a.On substituting the values of P and V from equation (16) and equation (17) in equation (12), one gets:
Here variation of X is from 0 to 1 and that of Y is from 0 to b/a.On substituting the values of P and V from equation (16) and equation (17) in equation (12), one gets: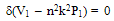 | (18) |
where 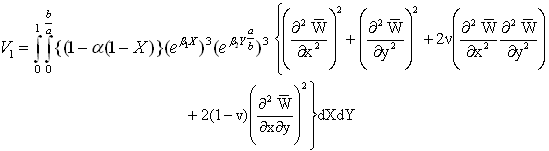 and
and 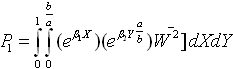 Here
Here 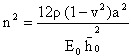 is a frequency parameter.Substitution of W from equation (14) in equation (18) gives rise to two unknown A1 and A2, which can be determined as follows:
is a frequency parameter.Substitution of W from equation (14) in equation (18) gives rise to two unknown A1 and A2, which can be determined as follows: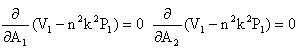 | (19) |
On solving we have: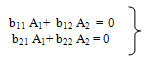 | (20) |
where b11, b12, b21, b22 involve parametric constants and the frequency parameter. The determinant of the coefficient of equation (20) must vanish for a non-trivial solution, therefore one gets, the frequency equation as: | (21) |
On solving equation (21) one gets a quadratic equation in k2, which gives two values of k2. On substituting the value of A1 = 1, by choice, in equation (14) one gets A2 = -b11/b12 and hence W becomes: 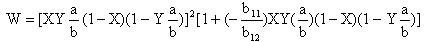 | (22) |
4. Time Function of Free Vibrations of Visco-Elastic Plate
The expression for Time function of free vibrations of visco-elastic plates of variable thickness can be derived from equation (5) that depends upon visco-elastic operator D and which for Kelvin’s Model can be taken as: 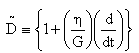 | (23) |
where η is visco-elastic constant and G is shear modulus. The temperature dependence of shear modulus G and visco-elastic constant η as is given by Gupta and Kumar[7]: 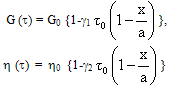 | (24) |
where G0 is shear modulus and η0 is visco-elastic constant at some reference temperature i.e. at τ = 0, γ1 and γ2 are slope variation of τ with G and η respectively. Substituting the value of τ from equation (6) and using equation (15) in equation (24), one gets: 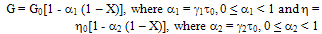 | (25) |
Here α1 and α2 are thermal constants.Substituting equations (23) and (25) in equation (5), one gets: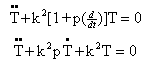 | (26) |
where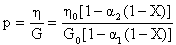 | (27) |
Equation (26) is a second order differential equation in time function T. The solution of which after applying initial condition T=1 and 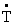 = 0, at t = 0, comes out to be:
= 0, at t = 0, comes out to be: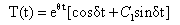 | (28) |
where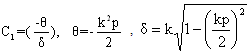 , Substituting equations (28) and (22) in equation (3), deflection w can be expressed as:
, Substituting equations (28) and (22) in equation (3), deflection w can be expressed as: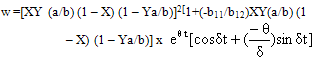 | (29) |
Time period of the vibration of the plate is given by:K = 2π/k , where k is frequency given by equation (21).
5. Numerical Calculations and Discussions
For calculations, the following material parameters of ‘Duralium’ which is an alloy of Aluminium, Copper, Magnesium and Manganese have been taken: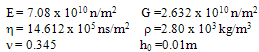 where h0 is the thickness of the plate taken at the centre. Computations have been made for calculating time period K and deflection w for different values of taper constants β1 and β2, aspect ratio a/b and thermal gradients α, α1 and α2 for the first two modes of vibration. All these results are shown in figures 1 to 7.In Fig.1, the results of time period K for a fixed value of aspect ratio a/b (=1.5) and for different thermal gradient α ranging from 0.0 to 1.0 with a difference of 0.2 but for all the values of X, Y and for all α1, α2 and for four combinations of β1 and β2 for the first two modes of vibration as follows:
where h0 is the thickness of the plate taken at the centre. Computations have been made for calculating time period K and deflection w for different values of taper constants β1 and β2, aspect ratio a/b and thermal gradients α, α1 and α2 for the first two modes of vibration. All these results are shown in figures 1 to 7.In Fig.1, the results of time period K for a fixed value of aspect ratio a/b (=1.5) and for different thermal gradient α ranging from 0.0 to 1.0 with a difference of 0.2 but for all the values of X, Y and for all α1, α2 and for four combinations of β1 and β2 for the first two modes of vibration as follows: 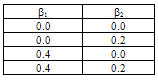 It can be clearly seen that as thermal gradient α increases, time period K increases continuously for both the modes of vibration.Fig.2 depicts the values of time period K for different values of aspect ratio a/b ranging from 0.5 to 2.5 with a difference of 0.5., and all values of X, Y and for all α1, α2 for both the modes of vibration having the following cases:
It can be clearly seen that as thermal gradient α increases, time period K increases continuously for both the modes of vibration.Fig.2 depicts the values of time period K for different values of aspect ratio a/b ranging from 0.5 to 2.5 with a difference of 0.5., and all values of X, Y and for all α1, α2 for both the modes of vibration having the following cases: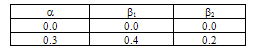 In both the cases, it can be seen that the value of time period K decreases as aspect ratio a/b increases for both the modes of vibration. It is clearly shown in fig.2 that time period K continuously decreased as aspect ratio a/b increased.Fig.3 shows the results of time period K, for the first two modes of vibration, for fixed aspect ratio a/b and for fixed thermal gradient α(=0.3) and for fixed value of taper constant β2(=0.2) for different values of taper constant β1 ranging from 0.0 to 1.0 with a difference of 0.2 but for all the values of X, Y and α1, α2. It can be noted that time period K decreases as taper constant β1 increase for both the modes of vibration. Fig. 3 supports the result of a steady decrease in time period K with increase in taper constants β1.The results of time period K, for the first two modes of vibration for fixed aspect ratio a/b, fixed thermal gradient α and for fixed value of taper constant β1 but for different values of taper constant β2 ranging from 0.0 to 1.0 with a difference of 0.2 and for all X, Y and α1, α2 are displayed in fig.4. For both the modes of vibration, time period K decreases with increase in taper constant β2.Figs.5 (a), 5(b) and 6(a), 6(b) respectively depict the variation of deflection w for different X for fixed aspect ratio a/b (=1.5) for the first two modes of vibration at initial time 0.K and time 5.K for different values of Y for the following cases:
In both the cases, it can be seen that the value of time period K decreases as aspect ratio a/b increases for both the modes of vibration. It is clearly shown in fig.2 that time period K continuously decreased as aspect ratio a/b increased.Fig.3 shows the results of time period K, for the first two modes of vibration, for fixed aspect ratio a/b and for fixed thermal gradient α(=0.3) and for fixed value of taper constant β2(=0.2) for different values of taper constant β1 ranging from 0.0 to 1.0 with a difference of 0.2 but for all the values of X, Y and α1, α2. It can be noted that time period K decreases as taper constant β1 increase for both the modes of vibration. Fig. 3 supports the result of a steady decrease in time period K with increase in taper constants β1.The results of time period K, for the first two modes of vibration for fixed aspect ratio a/b, fixed thermal gradient α and for fixed value of taper constant β1 but for different values of taper constant β2 ranging from 0.0 to 1.0 with a difference of 0.2 and for all X, Y and α1, α2 are displayed in fig.4. For both the modes of vibration, time period K decreases with increase in taper constant β2.Figs.5 (a), 5(b) and 6(a), 6(b) respectively depict the variation of deflection w for different X for fixed aspect ratio a/b (=1.5) for the first two modes of vibration at initial time 0.K and time 5.K for different values of Y for the following cases: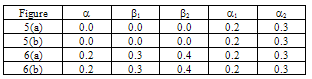 All these figures depict that deflection w for the first mode of vibration first increases and then decreases till zero as X increases for different values of Y. It can also be observed from all these figures that deflection w for the second mode of vibration, for Y = 0.2, first increases then decreases and then increases and finally becomes zero but for Y = 0.6, deflection w first increases and then decreases till zero as X increases.In fig.7, the variation of deflection w for different values of aspect ratio a/b, and for fixed values of X (= 0.2) and Y (= 0.2) at initial time 0.K and at time 5.K is shown for:
All these figures depict that deflection w for the first mode of vibration first increases and then decreases till zero as X increases for different values of Y. It can also be observed from all these figures that deflection w for the second mode of vibration, for Y = 0.2, first increases then decreases and then increases and finally becomes zero but for Y = 0.6, deflection w first increases and then decreases till zero as X increases.In fig.7, the variation of deflection w for different values of aspect ratio a/b, and for fixed values of X (= 0.2) and Y (= 0.2) at initial time 0.K and at time 5.K is shown for: From fig 7, it can be concluded that deflection w for the first mode of vibration continuously increases at initial time 0.K and first increases and then slightly decreases at the time 5.K but an increase followed by decrease is observed for second mode of vibration, with increase in aspect ratio a/b, at initial time 0.K and at time 5. K.
From fig 7, it can be concluded that deflection w for the first mode of vibration continuously increases at initial time 0.K and first increases and then slightly decreases at the time 5.K but an increase followed by decrease is observed for second mode of vibration, with increase in aspect ratio a/b, at initial time 0.K and at time 5. K.
Nomenclature
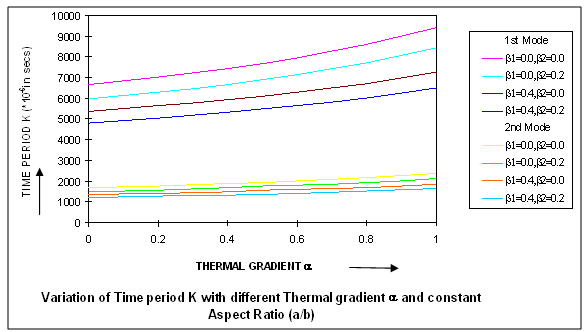 | Figure 1. Variation of Time period K with different Thermal Gradient α and Constant Aspect Ratio (a/b) |
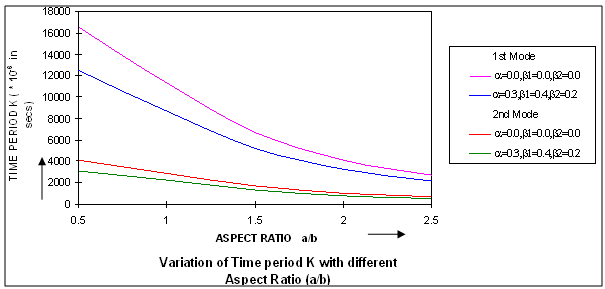 | Figure 2. Variation of Time period K with different Aspect Ratio (a/b) |
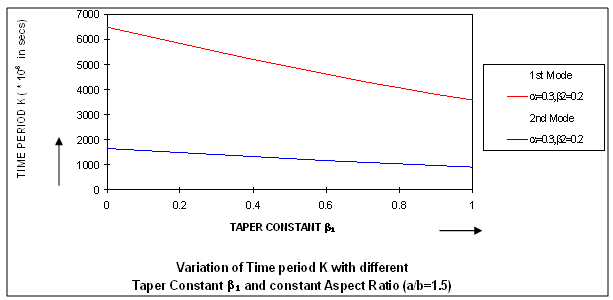 | Figure 3. Variation of Time period K with different Taper Constant β1 and Constant Aspect Ratio (a/b=1.5) |
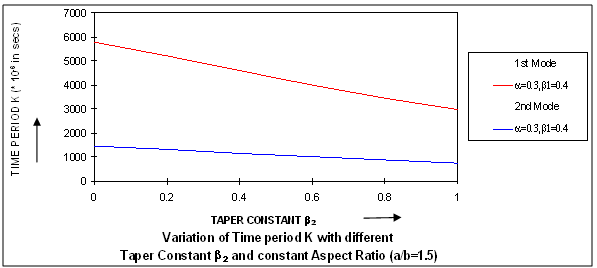 | Figure 4. Variation of Time period K with different taper constant β2 and Constant Aspect Ratio (a/b=1.5) |
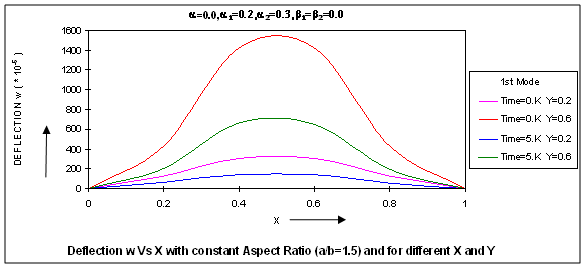 | Figure 5(a). Deflection W vs X with constant Aspect Ratio (a/b=1.5) and for different X and Y |
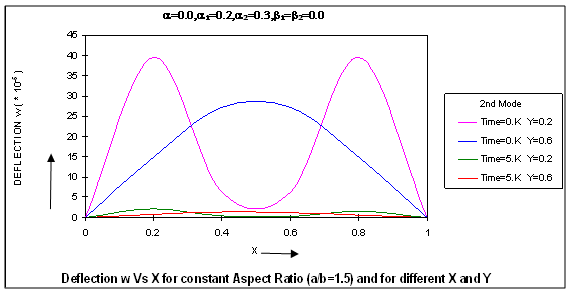 | Figure 5(b). Deflection W vs X for constant Aspect Ratio (a/b=1.5) and for different X and Y |
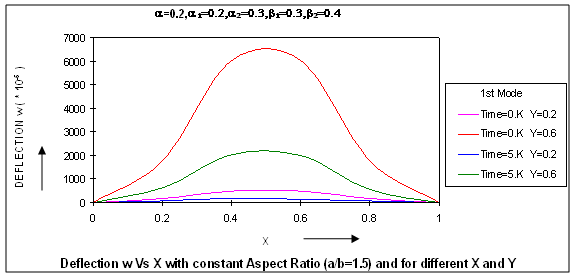 | Figure 6(a). Deflection W vs X with constant Aspect Ratio (a/b=1.5) and for different X and Y |
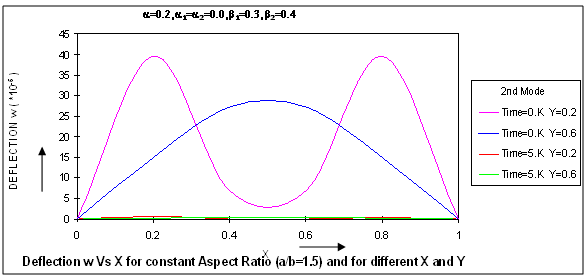 | Figure 6(b). Deflection w vs x for constant Aspect Ratio (a/b=1.5) and fordifferent X and Y |
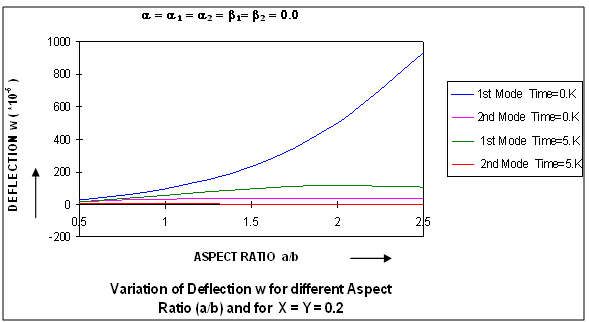 | Figure 7. Variation of deflection w for different Aspect Ratio (a/b) and for X=Y=0.2 |
6. Conclusions
It is concluded that as thermal gradient increases, time period increases continuously and hence frequency decreases for both the modes of vibration, therefore thermal effects can never be neglected. If thermal stresses are removed in the above case, the result match with the unheated plate in which temperature effect was not taken into account. After comparing authors conclude that as temperature effect introduced, time period and deflection increase gradually in comparison to unheated plate of varying thickness. Therefore engineers can see and develop the plates in the manner so that they can fulfil the requirements.
References
| [1] | Sobotka, Z. 'Free vibration of visco-elastic orthotropic rectangular plates', Acta.Technica, CSAV, No.6, pp.678-705, 1978. |
| [2] | Tomar, J.S. and Gupta, A.K. 'Thermal effect on frequencies of an orthotropic rectangular plate of linearly varying thickness', J. Sound and Vibration, Vol. 90(3), pp.325-331, 1983. |
| [3] | Singh, B. and Saxena, V. 'Transverse vibration of rectangular plate with bi-directional thickness variation', J. Sound and Vibration, Vol. 198(1), pp.51-65, 1996. |
| [4] | Gupta, A.K. and Khanna, A. ‘Vibration of visco-elastic rectangular plate with linearly thickness variation in both directions, J. Sound and Vibration, Vol. 301, pp.450-457, 2007. |
| [5] | Li., W.L. ‘Vibration analysis of rectangular plate with general elastic boundary supports’, J. Sound and Vibration, Vol. 273, pp.619-635, 2004. |
| [6] | Gupta, A.K. , Kumar, A. and Gupta, Y.K. ‘Vibration of visco elastic parallelogram plate with parabolic thickness variation’, Applied Mathematics, Vol.1, pp.128-136, 2010. |
| [7] | Gupta, A.K. and Kumar, L. ‘Effect of thermal gradient on vibration of non-homogeneous visco- elastic elliptic plate of variable thickness’, Meccanica, Vol. 44, pp.507-518, 2009. |
| [8] | Gupta, A.K. and Kumar, L. ‘Free vibration analysis of non-homogeneous visco-elastic circular plate with varying thickness subject to thermal gradient’, Acta Technica Vol.56, pp.217–232, 2011. |
| [9] | Leissa, A.W. 'Vibration of plates', NASA SP-160, U.S. Govt. Printing office, 1969. |
| [10] | Bhatnagar, N.S. and Gupta, A.K. 'Vibration analysis of visco-elastic circular plate subjected to thermal gradient’, Modeling, Simulation and Control, B, AMSE Press, Vol.15, No.1, pp.17-31, 1988 |
| [11] | Gupta, A.K. and Sharma, P. ‘Study of thermally induced vibration of non-homogeneous trapezoidal plate with varying thickness and density’, American Journal of Computational and Applied Mathematics, 2012. |

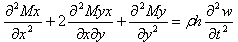
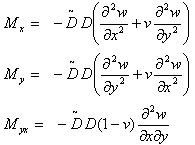
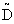 is Rheological operator and
is Rheological operator and 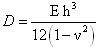 is flexural rigidity, in which ν is the Poisson’s ratio and E is Young modulus of elasticity.Since the thickness of the visco-elastic plate varies in two directions i.e. in x and y direction, consequently thickness h and flexural rigidity of the plate become function of x and y, therefore taking deflection w as a product of two functions as:
is flexural rigidity, in which ν is the Poisson’s ratio and E is Young modulus of elasticity.Since the thickness of the visco-elastic plate varies in two directions i.e. in x and y direction, consequently thickness h and flexural rigidity of the plate become function of x and y, therefore taking deflection w as a product of two functions as: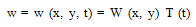
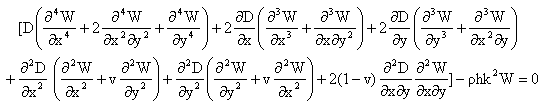
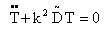
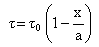
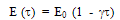
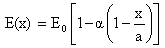
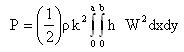
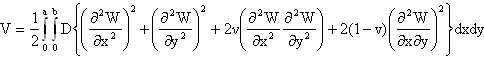
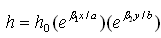
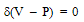
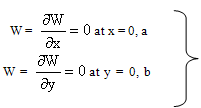
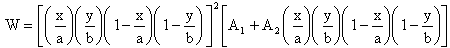
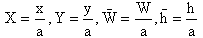
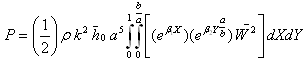
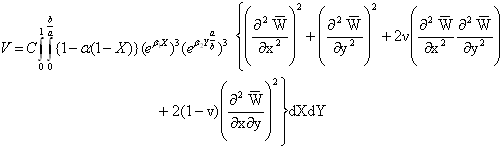
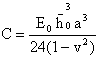 Here variation of X is from 0 to 1 and that of Y is from 0 to b/a.On substituting the values of P and V from equation (16) and equation (17) in equation (12), one gets:
Here variation of X is from 0 to 1 and that of Y is from 0 to b/a.On substituting the values of P and V from equation (16) and equation (17) in equation (12), one gets: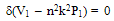
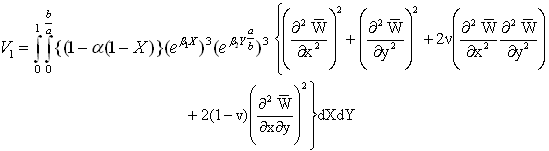 and
and 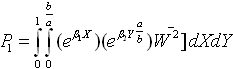 Here
Here 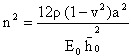 is a frequency parameter.Substitution of W from equation (14) in equation (18) gives rise to two unknown A1 and A2, which can be determined as follows:
is a frequency parameter.Substitution of W from equation (14) in equation (18) gives rise to two unknown A1 and A2, which can be determined as follows: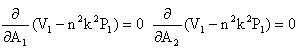
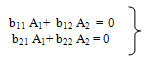

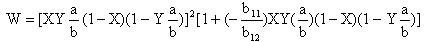
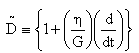
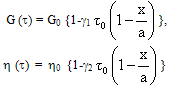
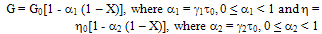
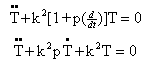
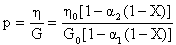
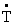 = 0, at t = 0, comes out to be:
= 0, at t = 0, comes out to be: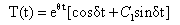
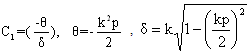 , Substituting equations (28) and (22) in equation (3), deflection w can be expressed as:
, Substituting equations (28) and (22) in equation (3), deflection w can be expressed as: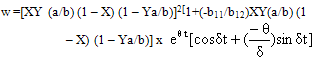
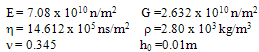 where h0 is the thickness of the plate taken at the centre. Computations have been made for calculating time period K and deflection w for different values of taper constants β1 and β2, aspect ratio a/b and thermal gradients α, α1 and α2 for the first two modes of vibration. All these results are shown in figures 1 to 7.In Fig.1, the results of time period K for a fixed value of aspect ratio a/b (=1.5) and for different thermal gradient α ranging from 0.0 to 1.0 with a difference of 0.2 but for all the values of X, Y and for all α1, α2 and for four combinations of β1 and β2 for the first two modes of vibration as follows:
where h0 is the thickness of the plate taken at the centre. Computations have been made for calculating time period K and deflection w for different values of taper constants β1 and β2, aspect ratio a/b and thermal gradients α, α1 and α2 for the first two modes of vibration. All these results are shown in figures 1 to 7.In Fig.1, the results of time period K for a fixed value of aspect ratio a/b (=1.5) and for different thermal gradient α ranging from 0.0 to 1.0 with a difference of 0.2 but for all the values of X, Y and for all α1, α2 and for four combinations of β1 and β2 for the first two modes of vibration as follows:  It can be clearly seen that as thermal gradient α increases, time period K increases continuously for both the modes of vibration.Fig.2 depicts the values of time period K for different values of aspect ratio a/b ranging from 0.5 to 2.5 with a difference of 0.5., and all values of X, Y and for all α1, α2 for both the modes of vibration having the following cases:
It can be clearly seen that as thermal gradient α increases, time period K increases continuously for both the modes of vibration.Fig.2 depicts the values of time period K for different values of aspect ratio a/b ranging from 0.5 to 2.5 with a difference of 0.5., and all values of X, Y and for all α1, α2 for both the modes of vibration having the following cases: In both the cases, it can be seen that the value of time period K decreases as aspect ratio a/b increases for both the modes of vibration. It is clearly shown in fig.2 that time period K continuously decreased as aspect ratio a/b increased.Fig.3 shows the results of time period K, for the first two modes of vibration, for fixed aspect ratio a/b and for fixed thermal gradient α(=0.3) and for fixed value of taper constant β2(=0.2) for different values of taper constant β1 ranging from 0.0 to 1.0 with a difference of 0.2 but for all the values of X, Y and α1, α2. It can be noted that time period K decreases as taper constant β1 increase for both the modes of vibration. Fig. 3 supports the result of a steady decrease in time period K with increase in taper constants β1.The results of time period K, for the first two modes of vibration for fixed aspect ratio a/b, fixed thermal gradient α and for fixed value of taper constant β1 but for different values of taper constant β2 ranging from 0.0 to 1.0 with a difference of 0.2 and for all X, Y and α1, α2 are displayed in fig.4. For both the modes of vibration, time period K decreases with increase in taper constant β2.Figs.5 (a), 5(b) and 6(a), 6(b) respectively depict the variation of deflection w for different X for fixed aspect ratio a/b (=1.5) for the first two modes of vibration at initial time 0.K and time 5.K for different values of Y for the following cases:
In both the cases, it can be seen that the value of time period K decreases as aspect ratio a/b increases for both the modes of vibration. It is clearly shown in fig.2 that time period K continuously decreased as aspect ratio a/b increased.Fig.3 shows the results of time period K, for the first two modes of vibration, for fixed aspect ratio a/b and for fixed thermal gradient α(=0.3) and for fixed value of taper constant β2(=0.2) for different values of taper constant β1 ranging from 0.0 to 1.0 with a difference of 0.2 but for all the values of X, Y and α1, α2. It can be noted that time period K decreases as taper constant β1 increase for both the modes of vibration. Fig. 3 supports the result of a steady decrease in time period K with increase in taper constants β1.The results of time period K, for the first two modes of vibration for fixed aspect ratio a/b, fixed thermal gradient α and for fixed value of taper constant β1 but for different values of taper constant β2 ranging from 0.0 to 1.0 with a difference of 0.2 and for all X, Y and α1, α2 are displayed in fig.4. For both the modes of vibration, time period K decreases with increase in taper constant β2.Figs.5 (a), 5(b) and 6(a), 6(b) respectively depict the variation of deflection w for different X for fixed aspect ratio a/b (=1.5) for the first two modes of vibration at initial time 0.K and time 5.K for different values of Y for the following cases: All these figures depict that deflection w for the first mode of vibration first increases and then decreases till zero as X increases for different values of Y. It can also be observed from all these figures that deflection w for the second mode of vibration, for Y = 0.2, first increases then decreases and then increases and finally becomes zero but for Y = 0.6, deflection w first increases and then decreases till zero as X increases.In fig.7, the variation of deflection w for different values of aspect ratio a/b, and for fixed values of X (= 0.2) and Y (= 0.2) at initial time 0.K and at time 5.K is shown for:
All these figures depict that deflection w for the first mode of vibration first increases and then decreases till zero as X increases for different values of Y. It can also be observed from all these figures that deflection w for the second mode of vibration, for Y = 0.2, first increases then decreases and then increases and finally becomes zero but for Y = 0.6, deflection w first increases and then decreases till zero as X increases.In fig.7, the variation of deflection w for different values of aspect ratio a/b, and for fixed values of X (= 0.2) and Y (= 0.2) at initial time 0.K and at time 5.K is shown for: From fig 7, it can be concluded that deflection w for the first mode of vibration continuously increases at initial time 0.K and first increases and then slightly decreases at the time 5.K but an increase followed by decrease is observed for second mode of vibration, with increase in aspect ratio a/b, at initial time 0.K and at time 5. K.
From fig 7, it can be concluded that deflection w for the first mode of vibration continuously increases at initial time 0.K and first increases and then slightly decreases at the time 5.K but an increase followed by decrease is observed for second mode of vibration, with increase in aspect ratio a/b, at initial time 0.K and at time 5. K. 









 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML