Hiroshi Matsuda
Faculty of Econoinformatic, Himeji Dokkyo University, 7-2-1, Kamiohno, Himeji, Hyogo, Japan
Correspondence to: Hiroshi Matsuda, Faculty of Econoinformatic, Himeji Dokkyo University, 7-2-1, Kamiohno, Himeji, Hyogo, Japan.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
Multiple-access adder channels have been extensively studied for manyyears. They can be classified into several types. The type of channels weconsider in this paper is discrete,memoryless, synchronized and noisy. On noisy multiple-access adder channels a receiver must derive a groupof transmitted codewords uniquely from a received word garbled by errors. Thismeans that a code suitable for this channel must have both separabilityand error control ability. In this paper we propose a coding method forsuch a channel.Our method utilizes some property of parity check matrices for Reeed-Solomon codes. We present not only encoding but also decoding methods of our codes. It is also shown that our method can construct some codes with high coding rates.
Keywords:
Multiple-Access Adder Channel, Error Correcting , Detecting, Wireless Communications
Cite this paper: Hiroshi Matsuda, Coding for a Noisy Binary Multiple-access Adder Channel, American Journal of Computational and Applied Mathematics, Vol. 3 No. 1, 2013, pp. 23-25. doi: 10.5923/j.ajcam.20130301.04.
1. Introduction
On the communication systems through a type of channels, some users can transmit each codeword, which is previously assigned to them, simultaneously. And the transmitted codewords are bitwisely added on the channels and therefore amount to a received word. Such channels are generally referred to as multiple-access adder channels.Multiple-access adder channels have been extensively studied for many years[1-3]. They can be classified into several typeson the basis of such a condition as arithmetic type of addition or noiseoccurring on a channel[4]. The type of channels we consider in this paper is discrete, memoryless, synchronized and noisy. And the arithmetictype of addition on a channel is modulo-2 addition. Moreover, assume that at most T users among M users (M>T) can transmit their codewords simultaneously. This type of communications is seen in wireless system such assatellite-based communication. Figure 1 shows thischannel model. In Figure 1 M, T, and Ci(i=1, 2, · · ·, M) mean the number of potential users, the maximum number of simultaneous connections andthe set of the codewords assigned to each user,respectively.A code suitable for this channel, therefore, must meet all the following conditions:1. A code can assign its codewords to all the potential Musers where M is much greater than the maximumnumber of simultaneous connections T.2. A code can derive all the codewords transmitted simultaneously from anoisy received word r.3. A code have error control ability to combat primary errors occurred on the channel.In general a type of primary errors we must combat varies agreat deal depending on some conditions such as channel characteristicsor how transmitted data are encoded in a codeword.In this paper we propose a coding method to meet all the conditions above.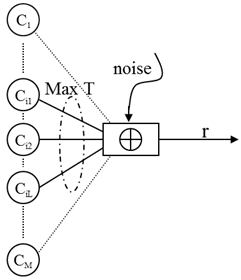 | Figure 1. Binary multiple-access adder channel with noise |
2. Coding Method
Firstly, we give a basic frame of our code by the use ofthe method indicated in[5].Let H be a parity check matrix of a Reed-Solomon code over GF(2m)that corrects T random errors and hi each column of the matrix H.Assigning each column to each user i , then, produces a code C0 whose codewordsare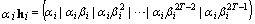 | (1) |
where αi is any nonzero element of GF(2m). After this we call each element of GF(2m) in a codeword or a received word a unit. It is obvious that for M = 2m-1 this code meets the above conditions 1 and 2 from the property of check matrix H[6]. So the code length n0 and coding rate R0 of this code C0are respectively given by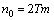 | (2) |
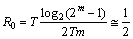 | (3) |
Note that this code has no error control ability. In the following we give a method to add error control ability to C0. Our codes have the following error control ability:(1) They can detect any odd weight errors on each unit in a codeword.(2) They can correct an error or detect two errors on a unit.Before describing our method we give conceptual diagram of our method in Figure 2.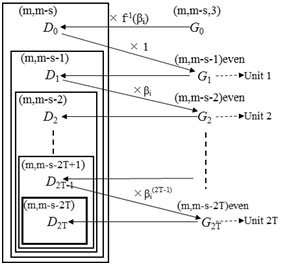 | Figure 2. Conceptual diagram of our method |
Let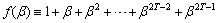 | (4) |
whereβ is any nonzero element of GF(2m).(1)For any nonzero elementβof GF(2m) such that f(β)≠0Suppose that a code (m,m-s,3)G0 is a binary code that has code length m and(m-s) information bits with minimum distance 3. Then, for any basis 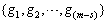 | (5) |
that spans this code over GF(2), 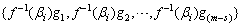 | (6) |
spans a (m,m-s) code D0overGF(2). All of the elements in (6) may have even weights. If not so, an even weight subcode of D0 can be always constructed by the following method:(1) If only one element in (6) has odd weight in GF(2) then the resulting (m-s-1) elements in (6) without the odd-weight element spans a (m, m-s-1, 2) even weight subcodes of D0. (2) If some elements in (6) have odd weights in GF(2) then adding of any odd-weight element selected from (6) and other odd-weight elements in (6) amounts to give a basis for a (m, m-s-1) even weight subcodes of D0.Since we want to give a lower bound on coding rate of our codes we shall use the above method to obtain even weight subcode. Now let D1 be the (m, m-s-1) even weight subcode of D0 stated above and B1 a basis of D0. The products of B1and a multiplier βi , then, spans a (m, m-s-1) code over GF(2). By the above method, hence, we can construct a (m, m-s-2) even weight subcode of D1, which is denoted by G2. Obviously a basis of G2 divided by βi spans a (m, m-s-2) subcode of D1. We denote this code by D2. Consequently, repeating this procedure by changing a multiplier from βi to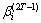 produces (m, m-s-2T) code D2T as shown in Figure 2. Finally, each user i uses non-zero codewords ofD2T as αi in (1). Then, since code Ds+1 is a subcode of Ds (s=0,1,2,…, 2T-1) it follows that each unit u (u = 1, 2,…,2T) in a codeword has even weight.(2) For any nonzero elementβof GF(2m) such that f(β)=0The procedure is the same as in (1) except starting with (m, m-1, 2) even weight codes as D1 and G1, respectively.Resultingly the code length n and coding rate R of our codesmeet the following expressions respectively.
produces (m, m-s-2T) code D2T as shown in Figure 2. Finally, each user i uses non-zero codewords ofD2T as αi in (1). Then, since code Ds+1 is a subcode of Ds (s=0,1,2,…, 2T-1) it follows that each unit u (u = 1, 2,…,2T) in a codeword has even weight.(2) For any nonzero elementβof GF(2m) such that f(β)=0The procedure is the same as in (1) except starting with (m, m-1, 2) even weight codes as D1 and G1, respectively.Resultingly the code length n and coding rate R of our codesmeet the following expressions respectively.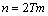 | (7) |
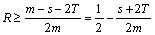 | (8) |
Note here that the numbers of the codewords each user ihas are always not the same: it depends on the element βi assigned to each user i. For example,when βi is equal to 1 the number of information bits assigned to user iism-1, which is always greater than m-s-2T. And when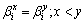 | (9) |
,code Dy+1 can be equal to code Dx+1 and this saves one parity check bit: whether Eq.(9) holds or not depends only the order of βi in GF(2m). In other cases,which code to be selected as G0 influences coding rate R since it might be possible that code D0 would be an even weight code.
3. Decoding and Numerical Results
In this section we prove the error control ability of our codes by giving a decoding method.<decoding method>[D1] Count the weight of each unit in a received word as an m-tuple overGF(2).[D2-1] If there are some units that have odd weight, then finish the decoding method: it means that some error occurred on not a unit but some units.[D2-2] If there is no unit or a unit that has odd weight, then add all units in a received word r as an m-tuple over GF(2) by modulo-2 addition. That is, for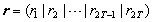 , calculate
, calculate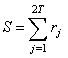 and decode S by any decoding method of G0. If the decoder decides that an error occurred, then correct the error on the unit detected by[D1]Obviously,[D2-1] is true because each unit in (1) must have even weight. From errors under consideration[D2-2] means that either no error or an error occurred on a unit. Hence if user ij(j=1,2,…,L-1,L;L≤T) in Figure 1 transmitted their codewords including αijas their information and an error e occurred on the channel, then
and decode S by any decoding method of G0. If the decoder decides that an error occurred, then correct the error on the unit detected by[D1]Obviously,[D2-1] is true because each unit in (1) must have even weight. From errors under consideration[D2-2] means that either no error or an error occurred on a unit. Hence if user ij(j=1,2,…,L-1,L;L≤T) in Figure 1 transmitted their codewords including αijas their information and an error e occurred on the channel, then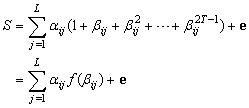 | (10) |
Since αij can be expressed as a product of 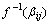 and a codeword of G0, S amounts to an addition of a codeword of G0 and e. This means that our codes have the error control ability stated above.As an example calculation we show the code length n and minimum coding rate R of our codes constructed by using a (2s-1, 2s-1-s, 3)Hamming code as G0. In this example coding rate RHmeets the following expression.
and a codeword of G0, S amounts to an addition of a codeword of G0 and e. This means that our codes have the error control ability stated above.As an example calculation we show the code length n and minimum coding rate R of our codes constructed by using a (2s-1, 2s-1-s, 3)Hamming code as G0. In this example coding rate RHmeets the following expression.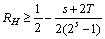 | (11) |
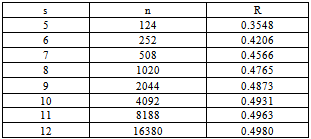
Table 1. Parameters of Our Codes Based on Hamming Codes (T=2)
 |
| |
|
This expression indicates that the coding rate of our code gets close to the same coding rate R0 of C0, which has no error control ability, as code lengh increases. In Table 1 we show some parameters of our codes based on Hamming codes when at most two users can transmit their codewords simultaneously.With increasing the number of active users the right hand of (11) gets smaller. But generally (4) tends to have more solutions in GF(2m) reversely. Coding rate, therefore, would be greater than one given by (11) when the users assigned the solutions of (4) as βi are included in potential users.
4. Conclusions
In this paper we have proposed a coding method for a noisybinary multiple-access adder channel. And by giving a decoding methodit has been shown that besides uniquely separable our codes have the property to control some errorsoccurred within a segment in a codeword and be uniquely separable whensome codewords superimposed. Furthermore it was shown that our codes can have coding rates close to the value which is associated with the uniquely separable codes without error control ability like[5]. As stated in this paper the selection of nonzero elements in GF(2m) assigned to each user affects coding rate in a direct fashion. So which element to be chosen is an important and interesting problem.It is also future work to expand our method to deal with several types of errors occurred on transmission.
References
| [1] | Alcoforado,M.L.M.G., da Rocha,V.C., Markarian,G., and Lima,M.J.C., “Iterative decoding of turbo convolutional codes over noisy two-user binaryadder channel “, Electron. Lett., 47, (1),pp. 749-751, 2011 |
| [2] | Lasse Kiviluoto and Patric R.J. Ostergard, “New Uniquely DecodableCodes for the T-User Binary Adder Channel With 3 ≤T≤5 “, IEEETrans.Inf.Theory,53,(3),pp. 1219-1220,1993, |
| [3] | Cheng,J., Ohira,T., Kamoi,K., andWatanabe,Y.,”Spreading SetWith ErrorCorrection for Multiple-Access Adder Channel “, IEEE Trans.Inf.Theory,52, (12),pp.5524-5529, 2006 |
| [4] | Mathys,P.”A Class of Codes for a T Active Users Out of N Multiple-AccessCommunication System”,IEEE Trans.Inf. Theory, 36, (6),pp.1206-1219, 1990 |
| [5] | Bar-David,I., Plotnik, E., and Rom, R.: “Forward collision resolutionatechnique for random multiple-access to the adder channel “, IEEETrans.Inf.Theory, 39, (5),pp.1671-1675,1993 |
| [6] | McWilliams,F.J., and Sloane, N.J.A.,The theory of error correcting codes, North-Holland Publishing Company,1977 |

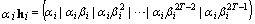
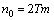
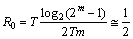

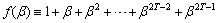
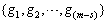
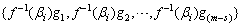
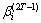 produces (m, m-s-2T) code D2T as shown in Figure 2. Finally, each user i uses non-zero codewords ofD2T as αi in (1). Then, since code Ds+1 is a subcode of Ds (s=0,1,2,…, 2T-1) it follows that each unit u (u = 1, 2,…,2T) in a codeword has even weight.(2) For any nonzero elementβof GF(2m) such that f(β)=0The procedure is the same as in (1) except starting with (m, m-1, 2) even weight codes as D1 and G1, respectively.Resultingly the code length n and coding rate R of our codesmeet the following expressions respectively.
produces (m, m-s-2T) code D2T as shown in Figure 2. Finally, each user i uses non-zero codewords ofD2T as αi in (1). Then, since code Ds+1 is a subcode of Ds (s=0,1,2,…, 2T-1) it follows that each unit u (u = 1, 2,…,2T) in a codeword has even weight.(2) For any nonzero elementβof GF(2m) such that f(β)=0The procedure is the same as in (1) except starting with (m, m-1, 2) even weight codes as D1 and G1, respectively.Resultingly the code length n and coding rate R of our codesmeet the following expressions respectively.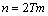
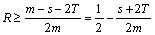
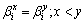
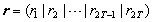 , calculate
, calculate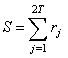 and decode S by any decoding method of G0. If the decoder decides that an error occurred, then correct the error on the unit detected by[D1]Obviously,[D2-1] is true because each unit in (1) must have even weight. From errors under consideration[D2-2] means that either no error or an error occurred on a unit. Hence if user ij(j=1,2,…,L-1,L;L≤T) in Figure 1 transmitted their codewords including αijas their information and an error e occurred on the channel, then
and decode S by any decoding method of G0. If the decoder decides that an error occurred, then correct the error on the unit detected by[D1]Obviously,[D2-1] is true because each unit in (1) must have even weight. From errors under consideration[D2-2] means that either no error or an error occurred on a unit. Hence if user ij(j=1,2,…,L-1,L;L≤T) in Figure 1 transmitted their codewords including αijas their information and an error e occurred on the channel, then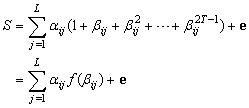
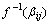 and a codeword of G0, S amounts to an addition of a codeword of G0 and e. This means that our codes have the error control ability stated above.As an example calculation we show the code length n and minimum coding rate R of our codes constructed by using a (2s-1, 2s-1-s, 3)Hamming code as G0. In this example coding rate RHmeets the following expression.
and a codeword of G0, S amounts to an addition of a codeword of G0 and e. This means that our codes have the error control ability stated above.As an example calculation we show the code length n and minimum coding rate R of our codes constructed by using a (2s-1, 2s-1-s, 3)Hamming code as G0. In this example coding rate RHmeets the following expression.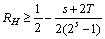
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML