-
Paper Information
- Next Paper
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Computational and Applied Mathematics
p-ISSN: 2165-8935 e-ISSN: 2165-8943
2013; 3(1): 13-22
doi:10.5923/j.ajcam.20130301.03
Iteratively Regularized Gradient Method for Determination of Source Terms in a Linear Parabolic Problem
Arzu Erdem
Kocaeli University, Faculty of Arts and Sciences, Department of Mathematics, Umuttepe Campus, 41380, Kocaeli, Turkey
Correspondence to: Arzu Erdem, Kocaeli University, Faculty of Arts and Sciences, Department of Mathematics, Umuttepe Campus, 41380, Kocaeli, Turkey.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
This paper investigates a numerical computation for determination of source terms in a linear parabolic problem. The source term 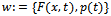 is defined in the linear parabolic equation
is defined in the linear parabolic equation 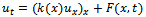 and Robin boundary condition
and Robin boundary condition 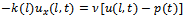 from the measured final data and the measurement of the temperature in a subregion. We demonstrate how to compute Fréchet derivative of Tikhonov functional based on the solution of the adjoint problem. Lipschitz continuity of the gradient is proved. Iteratively regularized gradient method is applied for numerical solution of the problem. We conclude with several numerical tests by using the theoretical results.
from the measured final data and the measurement of the temperature in a subregion. We demonstrate how to compute Fréchet derivative of Tikhonov functional based on the solution of the adjoint problem. Lipschitz continuity of the gradient is proved. Iteratively regularized gradient method is applied for numerical solution of the problem. We conclude with several numerical tests by using the theoretical results.
Keywords: Inverse Coefficient Source Problem, Parabolic Equation, Adjoint Problem, FrÉChet Derivative, Lipschitz Continuity
Cite this paper: Arzu Erdem, Iteratively Regularized Gradient Method for Determination of Source Terms in a Linear Parabolic Problem, American Journal of Computational and Applied Mathematics, Vol. 3 No. 1, 2013, pp. 13-22. doi: 10.5923/j.ajcam.20130301.03.
Article Outline
1. Introduction
- In describing the heat conduction in a material occupying a domain
 , the temperature distribution
, the temperature distribution 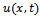 is modeled by
is modeled by  | (1) |
 | (2) |
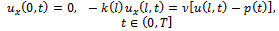 | (3) |
 denotes internal heat source,
denotes internal heat source,  is spatial varying heat conductivity,
is spatial varying heat conductivity, 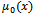 is an initial condition and
is an initial condition and  denotes the convection between conducting body and the ambient environment. If one cannot measure the pair
denotes the convection between conducting body and the ambient environment. If one cannot measure the pair  directly, one can try to determine
directly, one can try to determine 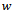 from the final state observation of
from the final state observation of 
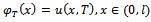 | (4) |
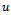 over subregion
over subregion 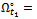
 ,
, 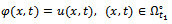 | (5) |
 has been investigated in[16,17]. To solve the inverse source problem one can use explicit and implicit methods[5,6,15,19,25]. Explicit methods provide analytical solutions to the inverse source problem directly from measured data. Explicit methods are limited to simple medium geometries with spatially non-varying optical parameters . For more complex geometries and heterogeneous media no explicit methods are available and implicit methods need to be employed. Implicit methods for solving the inverse source problem iteratively utilize a solution of a forward model to provide predicted measurement data. An update of an initial source distribution is sought by minimizing a functional that describes the goodness of a fit between the predicted and experimental data. Our approach is based on quasisolution approach. We also introduce an adjoint problem. Adjoint problem technique computes the gradient of the objective function. The concept of the adjoint problem technique can also be applied to similar inverse problems[10,13,14] or sensitivity analysis where the derivative of an error function is sought. A distinct advantage of using that technique is relatively simple numerical implementation and the resulting low computational costs. In view of quasisolution approach,this inverse problem can be formulated as minimization problem for the objective function[27]. In most cases for the numerical solution of this minimization problem gradient methods are used[4]. For this aim, in many applications various gradient formulas are either derived empirically, or computed numerically[21]. Although an empirical gradient formula has been employed with regularization algorithm,there was no mathematical framework for this formula. At the same time, we need to estimate the iteration parameter for any gradient method. Choice of the iteration parameter defines various gradient methods,although in many situation estimations of this parameter is a difficult problem. However,in the case of Lipschitz continuity of the gradient of the objective function the parameter can be estimated via the Lipschitz constant,which subsequently improves convergence properties of the iteration process [29]. In this paper we shall show how the adjoint problem technique can be readily utilized in proving Fréchet differentiability of the objective function. This has been hinted at in previous treatments[16]. Here we extend the objective function including the regularization parameter. Then we show how the Fréchet differentiability result is readily extended to examine Lipschitz continuity properties of the operator. Finally, we shall illustrate the application of our technique. The paper is outlined as follows. We summarize the basic notation and definition of regularized objective function in Section 2. Fréchet differentiability of the objective function results proven in Section 3 gives a unique regularized solution of the inverse problem. Iteratively regularized gradient method is proposed to obtain the numerical solution and some numerical examples are presented in Section 4 .
has been investigated in[16,17]. To solve the inverse source problem one can use explicit and implicit methods[5,6,15,19,25]. Explicit methods provide analytical solutions to the inverse source problem directly from measured data. Explicit methods are limited to simple medium geometries with spatially non-varying optical parameters . For more complex geometries and heterogeneous media no explicit methods are available and implicit methods need to be employed. Implicit methods for solving the inverse source problem iteratively utilize a solution of a forward model to provide predicted measurement data. An update of an initial source distribution is sought by minimizing a functional that describes the goodness of a fit between the predicted and experimental data. Our approach is based on quasisolution approach. We also introduce an adjoint problem. Adjoint problem technique computes the gradient of the objective function. The concept of the adjoint problem technique can also be applied to similar inverse problems[10,13,14] or sensitivity analysis where the derivative of an error function is sought. A distinct advantage of using that technique is relatively simple numerical implementation and the resulting low computational costs. In view of quasisolution approach,this inverse problem can be formulated as minimization problem for the objective function[27]. In most cases for the numerical solution of this minimization problem gradient methods are used[4]. For this aim, in many applications various gradient formulas are either derived empirically, or computed numerically[21]. Although an empirical gradient formula has been employed with regularization algorithm,there was no mathematical framework for this formula. At the same time, we need to estimate the iteration parameter for any gradient method. Choice of the iteration parameter defines various gradient methods,although in many situation estimations of this parameter is a difficult problem. However,in the case of Lipschitz continuity of the gradient of the objective function the parameter can be estimated via the Lipschitz constant,which subsequently improves convergence properties of the iteration process [29]. In this paper we shall show how the adjoint problem technique can be readily utilized in proving Fréchet differentiability of the objective function. This has been hinted at in previous treatments[16]. Here we extend the objective function including the regularization parameter. Then we show how the Fréchet differentiability result is readily extended to examine Lipschitz continuity properties of the operator. Finally, we shall illustrate the application of our technique. The paper is outlined as follows. We summarize the basic notation and definition of regularized objective function in Section 2. Fréchet differentiability of the objective function results proven in Section 3 gives a unique regularized solution of the inverse problem. Iteratively regularized gradient method is proposed to obtain the numerical solution and some numerical examples are presented in Section 4 . 2. Regularization Method
- Let us denote by
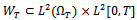 the set of admissible unknown sources
the set of admissible unknown sources  and
and 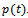 . The scalar product in
. The scalar product in 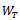 is defined as follows:
is defined as follows: 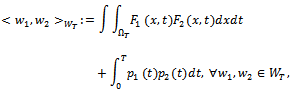 where
where  We also assume that
We also assume that . We denote the unique solution of problem (3) by
. We denote the unique solution of problem (3) by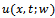 , corresponding to this source term. The direct problem could be to predict the evolution of the described system from knowledge of
, corresponding to this source term. The direct problem could be to predict the evolution of the described system from knowledge of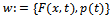 . We denote by
. We denote by 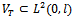 the set of measured output data
the set of measured output data 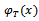 and
and 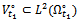 the set of measured output data
the set of measured output data 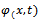 and set
and set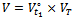 . Hence the inverse problem (3)-(4) can be formulated in the following operator form
. Hence the inverse problem (3)-(4) can be formulated in the following operator form  | (6) |
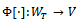 is defined to be the input-output mapping. We can give the definition of scalar product in
is defined to be the input-output mapping. We can give the definition of scalar product in  as similar as in
as similar as in 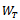 :
:  There is a fundamental difference between the direct and the inverse problems. In all cases, the inverse problem is ill-posed or improperly posed in the sense of Hadamard, while the direct problem is well-posed. A mathematical model for a physical problem is called as well-posed in the sense that it has the following three properties: There exists a solution of the problem (existence). There is at most one solution of the problem (uniqueness). The solution depends continuously on the data (stability). When the operator
There is a fundamental difference between the direct and the inverse problems. In all cases, the inverse problem is ill-posed or improperly posed in the sense of Hadamard, while the direct problem is well-posed. A mathematical model for a physical problem is called as well-posed in the sense that it has the following three properties: There exists a solution of the problem (existence). There is at most one solution of the problem (uniqueness). The solution depends continuously on the data (stability). When the operator 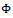 is a bounded, linear and injective between Hilbert spaces
is a bounded, linear and injective between Hilbert spaces 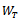 and
and , and
, and 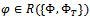 , the existence and uniqueness of the mapping is clear. If the desired output data
, the existence and uniqueness of the mapping is clear. If the desired output data 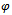 and
and 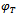 are not attainable, one tries to get approximation
are not attainable, one tries to get approximation 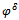 and
and 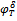 as close as possible
as close as possible  and
and 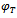 , respectively. Then the function
, respectively. Then the function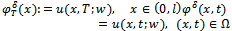 will be defined to be the final state noisy output data and the noisy data over the subregion. For the analysis of the approximation quality of the regularized solutions, we require that a bound on the data noise
will be defined to be the final state noisy output data and the noisy data over the subregion. For the analysis of the approximation quality of the regularized solutions, we require that a bound on the data noise 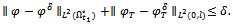 The problem to solve (3)-(4) with noise data
The problem to solve (3)-(4) with noise data  may be equivalently reformulated as finding the minimum of the functional which has been given in[16] for the only final state output data :
may be equivalently reformulated as finding the minimum of the functional which has been given in[16] for the only final state output data :  On the other hand, in the case where
On the other hand, in the case where 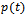 is given, the inverse problem of determining
is given, the inverse problem of determining 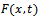 from the observation
from the observation 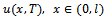 , can be transformed to a Fredholm equation of the second kind, where there might exist a non-trivial solution which implies the non-uniqueness for such an inverse problem. Of course, the solution to this minimization problem again does not depend continuously on the data. One possibility to restore stability is to add the data over the subregion and a penalty term to the functional involving the norm of
, can be transformed to a Fredholm equation of the second kind, where there might exist a non-trivial solution which implies the non-uniqueness for such an inverse problem. Of course, the solution to this minimization problem again does not depend continuously on the data. One possibility to restore stability is to add the data over the subregion and a penalty term to the functional involving the norm of :
: 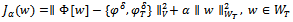 | (7) |
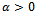 is called regularization parameter. A regularized solution
is called regularization parameter. A regularized solution  is defined by
is defined by  Regularization methods replace an ill-posed problem by a family of well-posed problems, their solution, called regularized solutions, are used as approximations to the desired solution of the inverse problem. These methods always involve some parameter measuring the closeness of the regularized and the original (unregularized) inverse problem, rules (and algorithms) for the choice of these regularization parameters as well as convergence properties of the regularized solutions are central points in the theory of these methods, since only they allow to finally and the right balance between stability and accuracy.
Regularization methods replace an ill-posed problem by a family of well-posed problems, their solution, called regularized solutions, are used as approximations to the desired solution of the inverse problem. These methods always involve some parameter measuring the closeness of the regularized and the original (unregularized) inverse problem, rules (and algorithms) for the choice of these regularization parameters as well as convergence properties of the regularized solutions are central points in the theory of these methods, since only they allow to finally and the right balance between stability and accuracy. 3. Properties of Regularization Method
- This section contains the main results of this paper. In the forthcoming theorem, we prove that the the functional (7) is Fréchet differentiable and provide the explicit form of the derivative. Let us give some preparations. Definition 3.1. Let X, Y be normed spaces, and let U be an open subset of X. A mapping
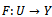 is called Fréchet differentiable at
is called Fréchet differentiable at 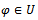 if there exists a bounded linear operator
if there exists a bounded linear operator 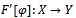 such that
such that 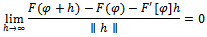 The proof of the following lemma can be found in[16]. Lemma 3.2. Let
The proof of the following lemma can be found in[16]. Lemma 3.2. Let  be two solutions of direct problem (3) corresponding to admissible sources
be two solutions of direct problem (3) corresponding to admissible sources
 The following equality holds:
The following equality holds: 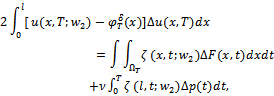 | (8) |
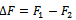 ,
,  ,
, 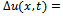
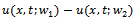 is the solution of the following sensitivity problem
is the solution of the following sensitivity problem 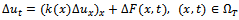 | (9) |
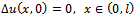 | (10) |
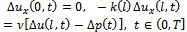 | (11) |
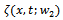 is the solution of the backward parabolic problem:
is the solution of the backward parabolic problem: 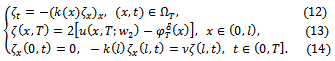 Lemma 3.3. Let
Lemma 3.3. Let  be two solutions of direct problem (3) corresponding to admissible sources
be two solutions of direct problem (3) corresponding to admissible sources
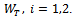 The following equality holds:
The following equality holds: 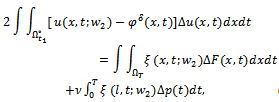 | (15) |
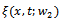 is the solution of the backward parabolic problem:
is the solution of the backward parabolic problem: 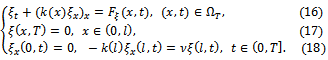 with the following discontinuous right-hand side
with the following discontinuous right-hand side 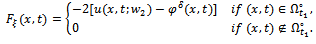 Proof. We start by replacing the left hand side of equality (15) with the right hand side of problem (18):
Proof. We start by replacing the left hand side of equality (15) with the right hand side of problem (18):  We use integration by parts
We use integration by parts 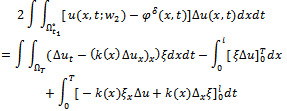 and employ initial and boundary conditions of problems (11) and (18) we conclude the proof of the lemma. The following Lemma gives computation of the first variation of the functional (7). Lemma 3.4. Let us denote by
and employ initial and boundary conditions of problems (11) and (18) we conclude the proof of the lemma. The following Lemma gives computation of the first variation of the functional (7). Lemma 3.4. Let us denote by
 .
. 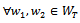 the first variation of the functional (7) is given by
the first variation of the functional (7) is given by 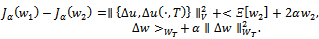 | (19) |
 Employing some add and subtract tricks, we get
Employing some add and subtract tricks, we get  Finally, this with the integral identities (8) and (15) leads to
Finally, this with the integral identities (8) and (15) leads to 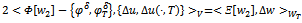 Lemma 3.5. There exists a constant
Lemma 3.5. There exists a constant 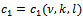 such that
such that  | (20) |
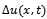 is solution of the parabolic problem (11). Proof. One can have this result due to Lemma 3.2 of[16]. Lemma 3.6. There exists a constant
is solution of the parabolic problem (11). Proof. One can have this result due to Lemma 3.2 of[16]. Lemma 3.6. There exists a constant 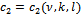 such that
such that 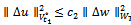 | (21) |
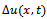 is solution of the parabolic problem (11). Proof. Due to the energy equality of the parabolic problem (11), we write
is solution of the parabolic problem (11). Proof. Due to the energy equality of the parabolic problem (11), we write 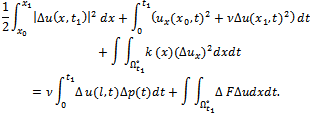 Applying Cauchy
Applying Cauchy  inequality to the right hand side of the above equality we obtain
inequality to the right hand side of the above equality we obtain 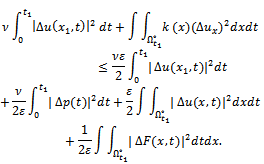 | (22) |
 we have
we have  | (23) |
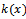 , we get the following estimate:
, we get the following estimate:  and satisfies
and satisfies  | (24) |
 . In this case requiring
. In this case requiring 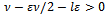 we obtain the bound
we obtain the bound 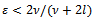 . Further from the requirement
. Further from the requirement 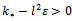 we have the second bound
we have the second bound 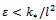 . Thus assuming for the parameter
. Thus assuming for the parameter 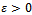
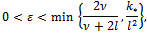 Taking into account (23) and (24)
Taking into account (23) and (24)  where
where 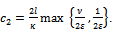 Theorem 3.7. Assume that
Theorem 3.7. Assume that 
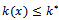 and
and  is the solution of the parabolic problem (11) corresponding to admissible source
is the solution of the parabolic problem (11) corresponding to admissible source 
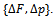 . Then, the functional (7) is Fréchet differentiable, with Fréchet differential:
. Then, the functional (7) is Fréchet differentiable, with Fréchet differential: 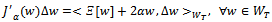 | (25) |
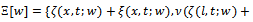
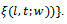 Proof. We take the two sources
Proof. We take the two sources 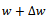 ,
, 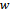 instead of
instead of 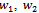 in (19)
in (19) 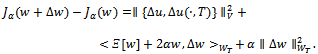 Using the estimates in lemma 5 and lemma 6 , we have
Using the estimates in lemma 5 and lemma 6 , we have 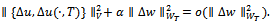 Then due to Definition 1 we conclude Fréchet derivative of the functional (7)
Then due to Definition 1 we conclude Fréchet derivative of the functional (7)  Theorem 3.8. If conditions of Theorem 7 hold, then the functional (7) has a unique solution
Theorem 3.8. If conditions of Theorem 7 hold, then the functional (7) has a unique solution  in
in 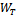 for
for  . This minimum is given by the solution of the following equation:
. This minimum is given by the solution of the following equation:  Moreover
Moreover  Proof. Assume that
Proof. Assume that 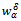 minimizes the functional (7). The choice
minimizes the functional (7). The choice 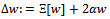 implies by (25) that
implies by (25) that 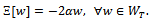 To show that
To show that 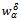 defined by the solution of above equation minimizes the functional (7), note that for all
defined by the solution of above equation minimizes the functional (7), note that for all 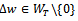 the function
the function  is a polynomial of degree 2 with
is a polynomial of degree 2 with 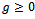 and
and 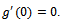 Hence
Hence 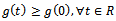 with the equality only
with the equality only 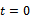 implies that
implies that 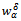 is a minimization of the functional (7). Due to the convexity of the functional (7), we obtain the uniqueness of the solution. Since the functional (7) attains its minimum at
is a minimization of the functional (7). Due to the convexity of the functional (7), we obtain the uniqueness of the solution. Since the functional (7) attains its minimum at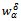 and
and 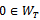 , we have
, we have  which implies
which implies  | (26) |
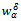 converges towards a solution of (6) in a set-valued sense with and
converges towards a solution of (6) in a set-valued sense with and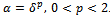 . Theorem 3.9. Let
. Theorem 3.9. Let 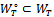 be a weakly closed set and
be a weakly closed set and  be the exact solution of (6) in
be the exact solution of (6) in  . If
. If 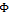 is injective and
is injective and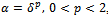 , then
, then 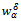 converges to
converges to 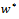 as
as 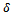 tends to zero. Proof. Let us assume the contrary. Then there exist an
tends to zero. Proof. Let us assume the contrary. Then there exist an  and a sequence
and a sequence 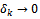 such that
such that 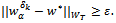 Since the functional (7) attains its minimum at
Since the functional (7) attains its minimum at 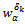
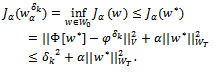 | (27) |
 | (28) |
 , such that
, such that  . Then we obtain
. Then we obtain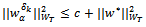 . Further, using the weak compactness of a ball in Hilbert space we conclude that
. Further, using the weak compactness of a ball in Hilbert space we conclude that  converges weakly to
converges weakly to 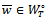 , since
, since  is a weakly closed subset. Together with lower semicontinuity of the norm and inequality (28)
is a weakly closed subset. Together with lower semicontinuity of the norm and inequality (28) 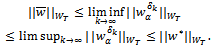 | (29) |
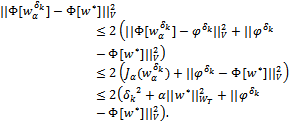 By limit transition as
By limit transition as , we conclude
, we conclude 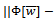
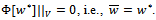 Due to the weak converges we obtain
Due to the weak converges we obtain 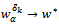 . This contradiction proves the theorem.
. This contradiction proves the theorem.4. Identification Process and Computational Results
- Another idea is to minimize the functional (7) by gradient method. This leads to the recursion formula of Conjugate Gradient Method
 | (30) |
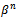 is the search step size,
is the search step size, 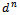 is the direction of descent,
is the direction of descent, 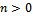 is the iteration parameter. The direction of descent
is the iteration parameter. The direction of descent  is given as
is given as  | (31) |
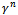 can be found as Polak-Ribiere or Fletcher -Reeves[1,7,11] . In the Polak-Ribiere version of the conjugation coefficient
can be found as Polak-Ribiere or Fletcher -Reeves[1,7,11] . In the Polak-Ribiere version of the conjugation coefficient 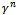 can be obtained from the following expression:
can be obtained from the following expression: 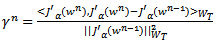 | (32) |
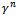 is given by the following expression:
is given by the following expression: 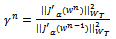 | (33) |

 | (34) |
 defined by (6) than just continuity. In particular to generate an affine approximation to
defined by (6) than just continuity. In particular to generate an affine approximation to  required to be Fréchet differentiable that we have already obtained in the previous section. To obtain high-order convergence properties of the numerical method this Fréchet derivative must also be Lipschitz continuous. For the next results we refer to[16,17] Theorem 4.1. If
required to be Fréchet differentiable that we have already obtained in the previous section. To obtain high-order convergence properties of the numerical method this Fréchet derivative must also be Lipschitz continuous. For the next results we refer to[16,17] Theorem 4.1. If 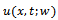 and
and 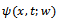 are the solutions of problems (3) and (14), respectively then
are the solutions of problems (3) and (14), respectively then  and the following estimate holds:
and the following estimate holds: 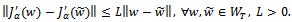 | (35) |
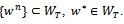 , Then
, Then  implies
implies  The proof of monotonicity of the sequence
The proof of monotonicity of the sequence 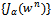 is given by Corollary 4.1 in[16]. Theorem 4.3. The sequence
is given by Corollary 4.1 in[16]. Theorem 4.3. The sequence 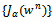 is a monotone decreasing sequence. Moreover;
is a monotone decreasing sequence. Moreover; 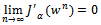 Since an expression for the gradient
Since an expression for the gradient 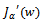 of the functional (7) is explicitly available, and easily obtained by solving the adjoint problem (14), the gradient can be readily implemented. Gradient algorithm[22] applied to the optimization problem takes the form Step 1 Choose
of the functional (7) is explicitly available, and easily obtained by solving the adjoint problem (14), the gradient can be readily implemented. Gradient algorithm[22] applied to the optimization problem takes the form Step 1 Choose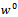 , and set
, and set . Step 2 Solve the direct problem (3) with
. Step 2 Solve the direct problem (3) with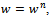 and determine the residuals
and determine the residuals 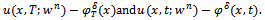 Step 3 Solve the adjoint problems (14) and (18) Step 4 Compute the gradient
Step 3 Solve the adjoint problems (14) and (18) Step 4 Compute the gradient 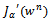 with (25). Step 5 Update the conjugation coefficient
with (25). Step 5 Update the conjugation coefficient  from (32) or (33) and then the direction descent
from (32) or (33) and then the direction descent  from (31). Step 6 By setting
from (31). Step 6 By setting 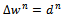 solve the sensitivity problem (11) to obtain
solve the sensitivity problem (11) to obtain  and
and 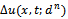 on subregion . Step 7 Compute the step size
on subregion . Step 7 Compute the step size 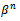 form (34). Step 8 Update
form (34). Step 8 Update 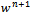 from (30). Step 9 Stop computing if the stopping criterion
from (30). Step 9 Stop computing if the stopping criterion  is satisfied. Otherwise set
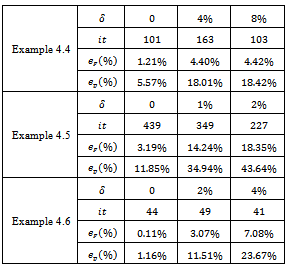
is satisfied. Otherwise set  and go to Step 2. Now, we perform some numerical experiments using the above algorithm. Example 4.4. In the first numerical experiment we take
and go to Step 2. Now, we perform some numerical experiments using the above algorithm. Example 4.4. In the first numerical experiment we take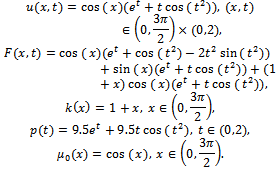 The final state observation and the observation over the subregion
The final state observation and the observation over the subregion 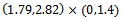 are given by
are given by  It is easy to check that
It is easy to check that 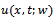 satisfies the problem (3) for
satisfies the problem (3) for . The noisy data
. The noisy data 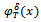 and
and  are generated as follows:
are generated as follows:  where
where 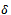 is the noisy level and
is the noisy level and 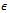 is generated by MATLAB function
is generated by MATLAB function . The exact solutions
. The exact solutions 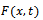 and
and  together with the numerical solutions for various values of the noisy level
together with the numerical solutions for various values of the noisy level 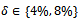 are shown in Figure 1. Due to the discrepancy principle we use the stopping criteria as
are shown in Figure 1. Due to the discrepancy principle we use the stopping criteria as 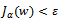 where the value of the tolerance
where the value of the tolerance
 , for noisy free data
, for noisy free data 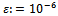 and the regularization parameter
and the regularization parameter 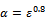 Example 4.5. In the second numerical experiment we take
Example 4.5. In the second numerical experiment we take 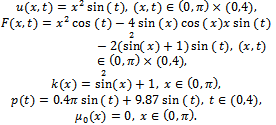 The final state observation and the observation over the subregion
The final state observation and the observation over the subregion  are given by
are given by 
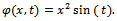
 satisfies the problem (3) for
satisfies the problem (3) for The exact solutions
The exact solutions  and
and  together with the numerical solutions for various values of the noisy level
together with the numerical solutions for various values of the noisy level 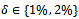 are presented in Figure 2. The stopping criteria is
are presented in Figure 2. The stopping criteria is  for noisy free data and the regularization parameter
for noisy free data and the regularization parameter 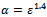
 | Figure 1. Results obtained by conjugate gradient method for Example 4.4 |
 | Figure 2. Exact solution and and numerical experiment of  and and 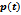 for various amounts of noise p ={1, 2}% for Example 4.5 for various amounts of noise p ={1, 2}% for Example 4.5 |
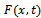 and
and 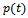 when an analytical solution for the problem (3) is not available:
when an analytical solution for the problem (3) is not available: 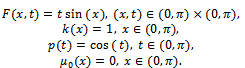 The final state observation and the observation over the subregion
The final state observation and the observation over the subregion 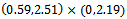 are computed by numerically for
are computed by numerically for . The exact solutions
. The exact solutions  and
and 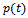 together with the numerical solutions for various values of the noisy level
together with the numerical solutions for various values of the noisy level 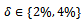 are presented in Figure 3. The stopping criteria is
are presented in Figure 3. The stopping criteria is 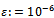 for noisy free data and the regularization parameter
for noisy free data and the regularization parameter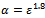 .
. 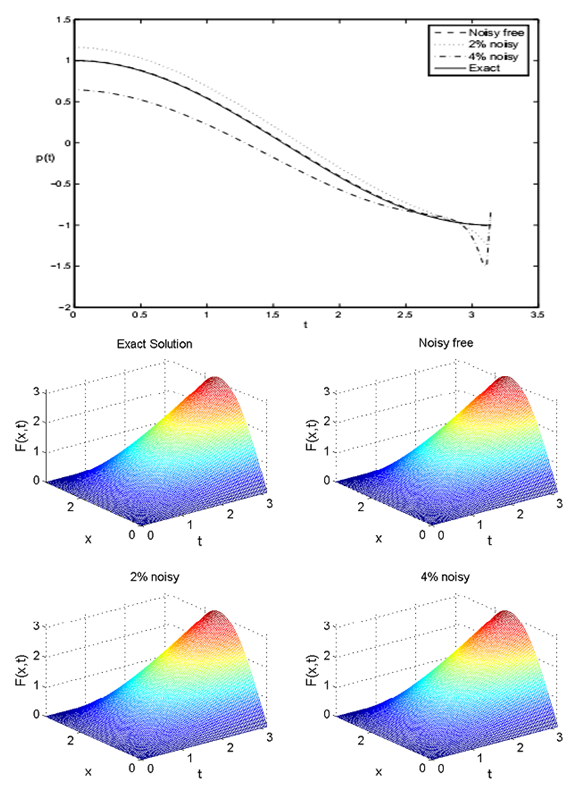 | Figure 3. Exact solution and construction of 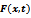 and and 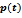 for various amounts of noise p ={2, 4}% for Example 4.6 for various amounts of noise p ={2, 4}% for Example 4.6 |
|
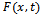 and
and . Here we use the symbol it as the stopping iteration numbers,
. Here we use the symbol it as the stopping iteration numbers, 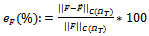 and
and 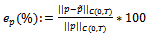 as the percentage error in
as the percentage error in 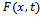 and
and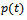 , respectively where
, respectively where  and
and 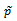 are approximate value of
are approximate value of 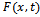 and
and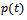 .
.  Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML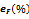 and
and 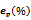 with various noisy level for Example4.4, Example4.5 and Example4.6
with various noisy level for Example4.4, Example4.5 and Example4.6