M. Y. Adamu, E. Suleiman
Mathematical Sciences programme, Abubakar Tafawa Balewa University, Bauchi, Nigeria
Correspondence to: M. Y. Adamu, Mathematical Sciences programme, Abubakar Tafawa Balewa University, Bauchi, Nigeria.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
The linear superposition principle of exponential travelling waves is analysed for equations of Hirota bilinear type, with an aim to construct a specific subclass of N-soliton solutions formed by linear combination of exponential travelling waves. Applications are made for Sawada-Kotera and a (2+1)-dimensional equations, thereby presenting their N-wave solutions. An opposite question is also put forward and discussed about generating Hirota bilinear equations possesses the indicated N-wave solutions and a few illustrative examples are presented, together with an algorithm using weights.
Keywords:
Hirota Bilinear Form, Soliton Equations, N-Wave Solution
Cite this paper: M. Y. Adamu, E. Suleiman, On Linear Superposition Principle Applying to Hirota Bilinear Equations, American Journal of Computational and Applied Mathematics, Vol. 3 No. 1, 2013, pp. 8-12. doi: 10.5923/j.ajcam.20130301.02.
1. Introduction
Searching for exact solution to nonlinear differential equations is significantly important in mathematical physics. Exact solution plays a vital role in understanding various qualitative and quantitative feature of nonlinear phenomenon. There are various classes of interesting exact solutions such as soliton and travelling wave solution, but it often needs for a specific mathematical technique to construct exact solution due to nonlinearity property in dynamics see[1]Among the various method for getting the exact solution of the nonlinear differential equations,[2,3,4], Hirota bilinear method provide a direct and powerful approach to nonlinear integrable equations and it is widely used in constructing soliton solution[5] . The existence of N-soliton solution often implies integrability of the considered differential equation[6, 7]. Interactions between solitons are elastic and nonlinear, but unfortunately, the linear superposition principle does not hold for soliton any more. However, bilinear equations are the nearest neighbours to linear equations, and expected to have some features similar to those of linear equations.In this paper, we would like extend the work[8, 9] to a (2+1)-dimensional and Sawada-Kotera equations in order to explore a key feature of the linear superposition principle that linear equations possess for Hirota bilinear equations while aiming to construct a specific sub-class of N-soliton solutions formed by linear combination of exponential travelling waves. Moreover as for integrable equations, there are detailed solution procedures by using determinant theories (see, e. g transaction of the nonlinear mathematical society 357(2005), 1753-1778 and applied mathematics and computation 217(2010), 10006-10013). To be specific, we will, in section two of the paper, prove that a linear superposition principle can be applied to exponential travelling waves of Hirota bilinear equations, while in section three an application procedure for generating Hirota bilinear equations possessing N-waves solutions of linear combinations of exponential waves will be treated and in section four we propose an opposite procedure for generating Hirota bilinear equations possess N-wave solutions of linear combinations of exponential waves, along with algorithm using weights as in[10, 11]. A few new and general such Hirota bilinear equations are computed. And finally the paper will be concluded in section 5.
2. Linear Superposition Principle
We begin with a Hirota bilinear equation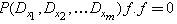 | (1) |
Where P is a polynomial in the indicated variables satisfying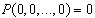 | (2) |
and 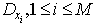 are Hirota’s differential operator defined by
are Hirota’s differential operator defined by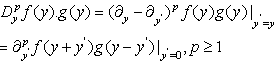 | (3) |
Various nonlinear equations of mathematical physics are written in Hirota form through a dependent variable transformationLet us introduce N wave variables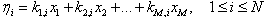 | (4) |
and N exponential wave function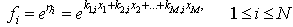 | (5) |
where 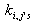 are constants. Observing that we have a bilinear identity
are constants. Observing that we have a bilinear identity  | (6) |
It follows immediately from (2) that exponential wave functions 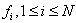 solves the Hirota bilinear equation (1).Now consider the N waves testing function
solves the Hirota bilinear equation (1).Now consider the N waves testing function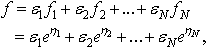 | (7) |
where 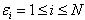 , are arbitrary constants. This is a general linear combination of N exponential travelling wave solutions. We supposed to have asked if it will present a solution to the Hirota bilinear equation (1) as each
, are arbitrary constants. This is a general linear combination of N exponential travelling wave solutions. We supposed to have asked if it will present a solution to the Hirota bilinear equation (1) as each 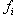 does. The answer is positive. We are going to show that a linear superposition principle of those exponential waves will apply to Hirota bilinear equations, under some additional conditions on the exponential waves and possibly on the polynomial p as well. Following (6) we can compute
does. The answer is positive. We are going to show that a linear superposition principle of those exponential waves will apply to Hirota bilinear equations, under some additional conditions on the exponential waves and possibly on the polynomial p as well. Following (6) we can compute | (8) |
The bilinear property will play a vital role in establishing the linear superposition principle for the exponential wave 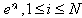 , we can directly see from (8) that any linear combination of exponential wave solution
, we can directly see from (8) that any linear combination of exponential wave solution 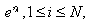 solves the Hirota bilinear equation (1) if the following condition
solves the Hirota bilinear equation (1) if the following condition 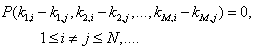 | (9) |
is satisfied. Here i = j is excluded, since it is a consequences of (3), the condition (9) gives us a system of nonlinear algebraic equations on the wave related numbers 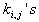 when the polynomial P is fixed. We will show that there is also a possibility of existence of solution for the variables
when the polynomial P is fixed. We will show that there is also a possibility of existence of solution for the variables 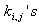 in lower dimension cases.Theorem 2 (linear superposition principle), let
in lower dimension cases.Theorem 2 (linear superposition principle), let 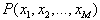 be a multivariate polynomial satisfying (3) and the wave, variables
be a multivariate polynomial satisfying (3) and the wave, variables 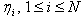 be defined by (3). then any linear combination of the exponential waves
be defined by (3). then any linear combination of the exponential waves 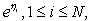 solves the Hirota bilinear equation (2) if condition (9) is satisfied.This shows a linear superposition principle of exponential wave solution that applies to hirota bilinear equations and paves a way of constructing N wave solutions from linear combination of exponential waves within the Hirota bilinear formalism. The system (9) is a key condition we need to handle. Once we get a solution of the wave related numbers
solves the Hirota bilinear equation (2) if condition (9) is satisfied.This shows a linear superposition principle of exponential wave solution that applies to hirota bilinear equations and paves a way of constructing N wave solutions from linear combination of exponential waves within the Hirota bilinear formalism. The system (9) is a key condition we need to handle. Once we get a solution of the wave related numbers 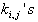 by solving (9), we can present an N wave solution formed by (7), to the considered nonlinear equation. Details of the theorem will be found in[8]Taking one of the variables
by solving (9), we can present an N wave solution formed by (7), to the considered nonlinear equation. Details of the theorem will be found in[8]Taking one of the variables , to be constant, for example, taking
, to be constant, for example, taking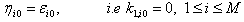 | (10) |
Where 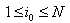 is fixed, the N wave solution conditions (9) subsequently requires all other wave related numbers to satisfy the dispersion relation
is fixed, the N wave solution conditions (9) subsequently requires all other wave related numbers to satisfy the dispersion relation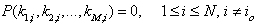 | (11) |
This corresponds to a specific case of N soliton solutions by the Hirota perturbation technique[6] truncated at the second order perturbation term. However, it is not generally necessary to satisfy the dispersion relation.
3. Application to Soliton Equations
We would like to consider two application examples of constructing the N-wave solutions by using the linear superposition principle in theorem (2).
3.1. Sawada-Kotera Equation
The first example to be considered is the Sawada-Kotera equation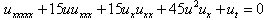 | (12) |
Through a dependent variable transformation 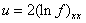 equation (10) can be written as
equation (10) can be written as 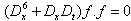 | (13) |
Which is equivalent to 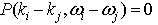 | (14) |
Assumed that the N-wave variables (4) are determined by 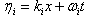 now since
now since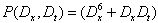 | (15) |
Then (9) becomes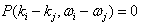 | (16) |
Which is equivalent to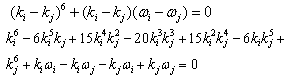 | (17) |
applying the dispersion relation 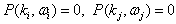 Then (3.6) becomes
Then (3.6) becomes 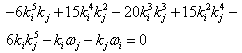 | (18) |
For i = j we have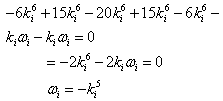 | (19) |
Hence 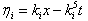 And therefor,e by the linear superposition principle in theorem (2.1) the Sawada-Kotera equation (3.1) has the following N-wave solutions
And therefor,e by the linear superposition principle in theorem (2.1) the Sawada-Kotera equation (3.1) has the following N-wave solutions 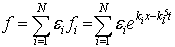 using
using 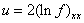 Where
Where 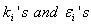 are arbitrary constant.
are arbitrary constant.
3.2. (2+1)-Dimensional Equation
The (2+1)-dimensional equation 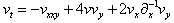 | (20) |
can be transformed in to 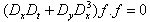 | (21) |
Using a dependent variable transformation 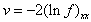 Assumed the N-wave variables are determined by
Assumed the N-wave variables are determined by 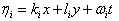 Then
Then 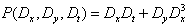 Therefore, (9) becomes
Therefore, (9) becomes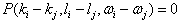 | (22) |
Using (9) we have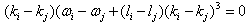 | (23) |
Expanding and applying the dispersion relation 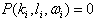
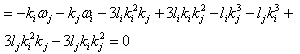 For i = j we have
For i = j we have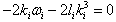 Solving to get
Solving to get 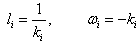 Hence by linear superposition in theorem (2) the (2+1)-dimensional equation (18) has the following N-wave equation
Hence by linear superposition in theorem (2) the (2+1)-dimensional equation (18) has the following N-wave equation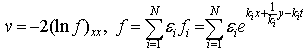
4. An Opposite Question
Here we will like also to apply the algorithm proposed by[8] in order to construct an opposite procedure for conversely constructing Hirota bilinear equations possesses N-wave solutions formed by linear combinations of exponential waves. This is an opposite question on applying the linear superposition principle in theorem 2We first find a multivariate polynomial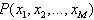 ) with no constant term such that
) with no constant term such that 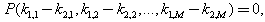 | (24) |
for two parameters 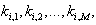 i – 1,2. Each of which would better contain at least one free parameter. Then formulate a Hirota bilinear equation through (2) using the polynomial P. Theorem 2 tells that the resulting Hirota bilinear equation posses multiple wave solution of linear combination of exponential travelling waves. Such as multivariate polynomial P can be normally found by balancing the involved free parameter in (24), and sometimes upon assuming that two sets of parameters satisfy the dispersion relation
i – 1,2. Each of which would better contain at least one free parameter. Then formulate a Hirota bilinear equation through (2) using the polynomial P. Theorem 2 tells that the resulting Hirota bilinear equation posses multiple wave solution of linear combination of exponential travelling waves. Such as multivariate polynomial P can be normally found by balancing the involved free parameter in (24), and sometimes upon assuming that two sets of parameters satisfy the dispersion relation 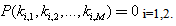 | (25) |
Examples of equations expressed in fAn algorithm can be given to use the concept of weights, to compute examples of Hirota bilinear equations that possess the linear superposition principle of exponential waves. Let us first define the weights of independent variables 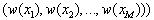 where each weight
where each weight 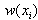 is an integer, and then form homogenous polynomials
is an integer, and then form homogenous polynomials 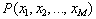 of some weights to check if it will still satisfy the condition (24). The simplest way to start our checking is to assume that the weights variables
of some weights to check if it will still satisfy the condition (24). The simplest way to start our checking is to assume that the weights variables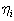 ’s involve arbitrary constants. This way we can compare power of those arbitrary constants in (24) to obtain algebraic equations on other constants and/or coefficients to solve. The following are some examples which apply the algorithm using weights.Examples with N-waves satisfy the dispersion relationExample 1 weights
’s involve arbitrary constants. This way we can compare power of those arbitrary constants in (24) to obtain algebraic equations on other constants and/or coefficients to solve. The following are some examples which apply the algorithm using weights.Examples with N-waves satisfy the dispersion relationExample 1 weights 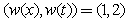 Let us first introduce the weights of independent variables
Let us first introduce the weights of independent variables 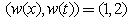 Then a general homogenous polynomials of weights 2 is
Then a general homogenous polynomials of weights 2 is 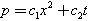 | (26) |
Assume that the weights variables are 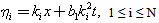 | (27) |
where 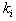 ’s are arbitrary constants but
’s are arbitrary constants but 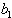 is a constant to be determined this way, a direct computation tells that the corresponding Hirota bilinear equation
is a constant to be determined this way, a direct computation tells that the corresponding Hirota bilinear equation 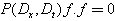 possesses an N-wave solution
possesses an N-wave solution 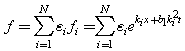 | (28) |
Where, 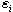 ’s and
’s and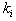 ’s are arbitrary but
’s are arbitrary but 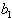 satisfies
satisfies 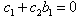 | (29) |
and has the N-wave solution defined (28) with 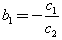 Example 2. Weights
Example 2. Weights 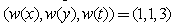 Let us secondly, introduce the weights of independent variables:Weights
Let us secondly, introduce the weights of independent variables:Weights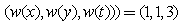 Then, a general homogenous polynomial of weights 3 reads
Then, a general homogenous polynomial of weights 3 reads 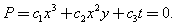 | (30) |
Assume that the wave variables are 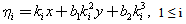 | (31) |
where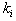 ’s 1 ≤ i ≤ N, are arbitrary constants but
’s 1 ≤ i ≤ N, are arbitrary constants but 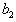 and
and 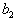 are constant to be determined. This way a direct computation tells us that the corresponding Hirota bilinear equation
are constant to be determined. This way a direct computation tells us that the corresponding Hirota bilinear equation 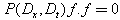 possesses the N-wave solution.
possesses the N-wave solution.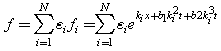 | (32) |
Where, 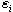 ’s and
’s and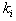 ’s are arbitrary but
’s are arbitrary but 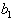 and
and 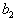 satisfy
satisfy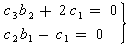 | (33) |
And the N-wave solution defined by (32) with 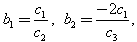 Examples with N-wave not satisfying the dispersion relationWeights
Examples with N-wave not satisfying the dispersion relationWeights 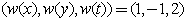 Let us finally introduce the weights of independent variables Weights
Let us finally introduce the weights of independent variables Weights 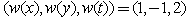 Then, the homogenous polynomial of weights 2 reads
Then, the homogenous polynomial of weights 2 reads 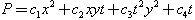 | (34) |
Assume that the wave variables are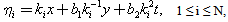 | (35) |
Where 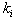 are arbitrary but
are arbitrary but 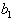 and
and 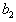 are constants to be determined.Now a similar direct computation tells that the corresponding Hirota bilinear equation
are constants to be determined.Now a similar direct computation tells that the corresponding Hirota bilinear equation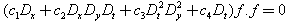 | (36) |
Possesses an N-wave solution 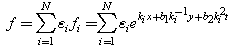 | (37) |
Where, 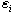 ’s and
’s and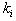 ’s are arbitrary but
’s are arbitrary but 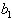 and
and 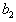 satisfy
satisfy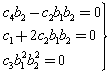 | (38) |
The taking 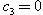 tells that the Hirota bilinear equation
tells that the Hirota bilinear equation 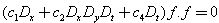 | (39) |
Has N- wave solution defined by (34) With 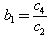 and
and 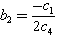 Example 2. weights
Example 2. weights 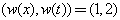 Let us first introduce the weights of independent variables
Let us first introduce the weights of independent variables 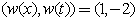 Then general homogenous polynomials of weights 1 is
Then general homogenous polynomials of weights 1 is 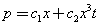 | (40) |
assume that the weights variables are 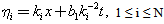 | (41) |
where 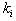 ’s are arbitrary constants but
’s are arbitrary constants but 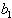 is a constant to be determined.Now, a similar direct computation tells that the corresponding Hirota bilinear equation
is a constant to be determined.Now, a similar direct computation tells that the corresponding Hirota bilinear equation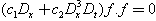 | (42) |
Possesses N-wave solution 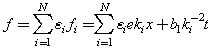 | (43) |
Where, 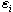 ’s and
’s and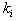 ’s are arbitrary but
’s are arbitrary but 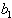 satisfy
satisfy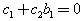 With
With 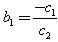 .
.
5. Conclusions
Following the procedure proposed by[8], we have analyzed a specific sub-class of N-soliton solutions, formed by a linear combination of exponential travelling waves, for sawada-Kotera and a (2+1)-dimensional equations. The starting point is to solve a system of nonlinear algebraic equations for the wave related numbers called the N-wave solution condition. The resulting system tells what Hirota bilinear equation the linear superposition principle of exponential wave will apply to. Though it was shown that, high dimensional Hirota bilinear equations have a better opportunity to satisfy the N-wave solution condition because of their large parameters to choose from[10], we were able to also show for the lower dimensional Hirota bilinear equations. We also showed that linear superposition principle can hold for some special kind of wave solutions to Hirota bilinear equations, for example the exponential wave as we have explored. This also tells us why Hirota bilinear methods have advantages over some of the other methods
References
| [1] | Ma. W. X, Diversity of exact solution to a restricted Boiti-Leon-pempinelli dispersive long way system. Physics. Letter. A 310 325-333 2003 |
| [2] | Airy, S., Stokes, J., Boussinesq, V. and Raleigh, H., , Investigation of solitary waves solitons, nonlinear evolution equation and inverse scattering ,London mathematical society lecture series 149, 1991 Cambridge Univ. Press London |
| [3] | Freeman, N. C. and. Nimmo, J.J.C, The use of Backlund transformation in obtaining N-soliton solutions in Wronskian form. Phyicss letter. A 95, 1-3. 1983. |
| [4] | Darvishi, M. T. Najafi, M. And Najafi, M, Application of multiple Exp-function method to obtain multiple soliton solutions of (2+1)- and (3+1)-dimensional breaking soliton equations. American Journal of Computational And Appllied Mathematics1(2) 41-48 .(2011), |
| [5] | Jimbo, M and Miwa. T, solitons and infinite dimensional Lie algebra publication of Reearch Institute of Mathematical Science. 19, 943-1001. 1983 |
| [6] | R. Hirota. The Direct Method in Soliton Theory. (2004) Cambridge University Press |
| [7] | Hietarinta.J Hirota’’s bilinear method and soliton solutions. Physics AUC 15 (part 1) 31-37. 2005 |
| [8] | Ma, W. X. Huang, T. W. and.Zhang, Y, A multiple Exp-function Method for nonlinear differential equations and its application Physica. Scripta 82, 065003, 2010 |
| [9] | Ma. W. X. and Fan, E, Linear superposition principle applying to Hirota bilionear equations. Computer And Mathematics With Appllications. 61, 950-959 .2011 |
| [10] | Ma, W. X. Zhang .Y, Tang, Y. and Tu, T. (2012), Hirota bilinear equations with linear subspaces of solutions. Appllied Mathematics and Computer. 218, 7174-7183. |
| [11] | M. Y Adamu, and E. Suleiman,, Linear Subspace of solution applied to Hirota bilinear equations, Aceh International Journal of Science and technology, 1 (2) 45-51 2012 |
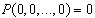
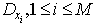 are Hirota’s differential operator defined by
are Hirota’s differential operator defined by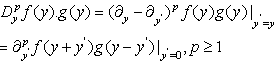
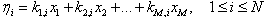
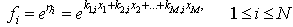
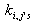 are constants. Observing that we have a bilinear identity
are constants. Observing that we have a bilinear identity 
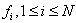 solves the Hirota bilinear equation (1).Now consider the N waves testing function
solves the Hirota bilinear equation (1).Now consider the N waves testing function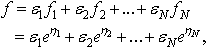
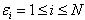 , are arbitrary constants. This is a general linear combination of N exponential travelling wave solutions. We supposed to have asked if it will present a solution to the Hirota bilinear equation (1) as each
, are arbitrary constants. This is a general linear combination of N exponential travelling wave solutions. We supposed to have asked if it will present a solution to the Hirota bilinear equation (1) as each 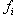 does. The answer is positive. We are going to show that a linear superposition principle of those exponential waves will apply to Hirota bilinear equations, under some additional conditions on the exponential waves and possibly on the polynomial p as well. Following (6) we can compute
does. The answer is positive. We are going to show that a linear superposition principle of those exponential waves will apply to Hirota bilinear equations, under some additional conditions on the exponential waves and possibly on the polynomial p as well. Following (6) we can compute
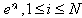 , we can directly see from (8) that any linear combination of exponential wave solution
, we can directly see from (8) that any linear combination of exponential wave solution 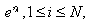 solves the Hirota bilinear equation (1) if the following condition
solves the Hirota bilinear equation (1) if the following condition 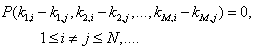
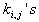 when the polynomial P is fixed. We will show that there is also a possibility of existence of solution for the variables
when the polynomial P is fixed. We will show that there is also a possibility of existence of solution for the variables 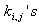 in lower dimension cases.Theorem 2 (linear superposition principle), let
in lower dimension cases.Theorem 2 (linear superposition principle), let 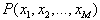 be a multivariate polynomial satisfying (3) and the wave, variables
be a multivariate polynomial satisfying (3) and the wave, variables 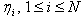 be defined by (3). then any linear combination of the exponential waves
be defined by (3). then any linear combination of the exponential waves 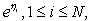 solves the Hirota bilinear equation (2) if condition (9) is satisfied.This shows a linear superposition principle of exponential wave solution that applies to hirota bilinear equations and paves a way of constructing N wave solutions from linear combination of exponential waves within the Hirota bilinear formalism. The system (9) is a key condition we need to handle. Once we get a solution of the wave related numbers
solves the Hirota bilinear equation (2) if condition (9) is satisfied.This shows a linear superposition principle of exponential wave solution that applies to hirota bilinear equations and paves a way of constructing N wave solutions from linear combination of exponential waves within the Hirota bilinear formalism. The system (9) is a key condition we need to handle. Once we get a solution of the wave related numbers 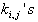 by solving (9), we can present an N wave solution formed by (7), to the considered nonlinear equation. Details of the theorem will be found in[8]Taking one of the variables
by solving (9), we can present an N wave solution formed by (7), to the considered nonlinear equation. Details of the theorem will be found in[8]Taking one of the variables , to be constant, for example, taking
, to be constant, for example, taking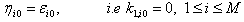
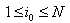 is fixed, the N wave solution conditions (9) subsequently requires all other wave related numbers to satisfy the dispersion relation
is fixed, the N wave solution conditions (9) subsequently requires all other wave related numbers to satisfy the dispersion relation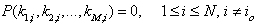
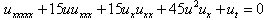
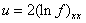 equation (10) can be written as
equation (10) can be written as 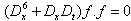
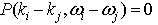
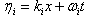 now since
now since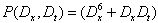
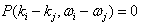
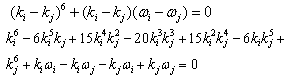
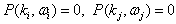 Then (3.6) becomes
Then (3.6) becomes 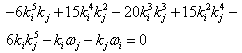
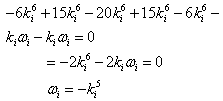
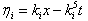 And therefor,e by the linear superposition principle in theorem (2.1) the Sawada-Kotera equation (3.1) has the following N-wave solutions
And therefor,e by the linear superposition principle in theorem (2.1) the Sawada-Kotera equation (3.1) has the following N-wave solutions 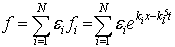 using
using 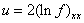 Where
Where 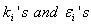 are arbitrary constant.
are arbitrary constant.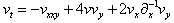
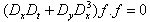
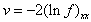 Assumed the N-wave variables are determined by
Assumed the N-wave variables are determined by 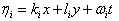 Then
Then 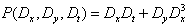 Therefore, (9) becomes
Therefore, (9) becomes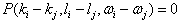
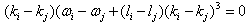
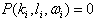
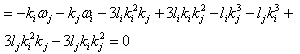 For i = j we have
For i = j we have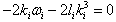 Solving to get
Solving to get 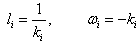 Hence by linear superposition in theorem (2) the (2+1)-dimensional equation (18) has the following N-wave equation
Hence by linear superposition in theorem (2) the (2+1)-dimensional equation (18) has the following N-wave equation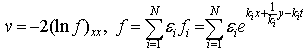
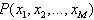 ) with no constant term such that
) with no constant term such that 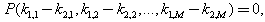
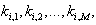 i – 1,2. Each of which would better contain at least one free parameter. Then formulate a Hirota bilinear equation through (2) using the polynomial P. Theorem 2 tells that the resulting Hirota bilinear equation posses multiple wave solution of linear combination of exponential travelling waves. Such as multivariate polynomial P can be normally found by balancing the involved free parameter in (24), and sometimes upon assuming that two sets of parameters satisfy the dispersion relation
i – 1,2. Each of which would better contain at least one free parameter. Then formulate a Hirota bilinear equation through (2) using the polynomial P. Theorem 2 tells that the resulting Hirota bilinear equation posses multiple wave solution of linear combination of exponential travelling waves. Such as multivariate polynomial P can be normally found by balancing the involved free parameter in (24), and sometimes upon assuming that two sets of parameters satisfy the dispersion relation 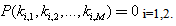
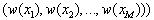 where each weight
where each weight 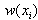 is an integer, and then form homogenous polynomials
is an integer, and then form homogenous polynomials 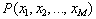 of some weights to check if it will still satisfy the condition (24). The simplest way to start our checking is to assume that the weights variables
of some weights to check if it will still satisfy the condition (24). The simplest way to start our checking is to assume that the weights variables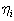 ’s involve arbitrary constants. This way we can compare power of those arbitrary constants in (24) to obtain algebraic equations on other constants and/or coefficients to solve. The following are some examples which apply the algorithm using weights.Examples with N-waves satisfy the dispersion relationExample 1 weights
’s involve arbitrary constants. This way we can compare power of those arbitrary constants in (24) to obtain algebraic equations on other constants and/or coefficients to solve. The following are some examples which apply the algorithm using weights.Examples with N-waves satisfy the dispersion relationExample 1 weights 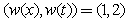 Let us first introduce the weights of independent variables
Let us first introduce the weights of independent variables 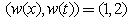 Then a general homogenous polynomials of weights 2 is
Then a general homogenous polynomials of weights 2 is 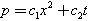
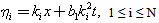
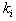 ’s are arbitrary constants but
’s are arbitrary constants but 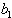 is a constant to be determined this way, a direct computation tells that the corresponding Hirota bilinear equation
is a constant to be determined this way, a direct computation tells that the corresponding Hirota bilinear equation 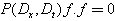 possesses an N-wave solution
possesses an N-wave solution 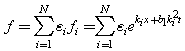
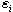 ’s and
’s and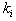 ’s are arbitrary but
’s are arbitrary but 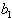 satisfies
satisfies 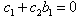
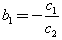 Example 2. Weights
Example 2. Weights 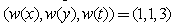 Let us secondly, introduce the weights of independent variables:Weights
Let us secondly, introduce the weights of independent variables:Weights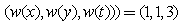 Then, a general homogenous polynomial of weights 3 reads
Then, a general homogenous polynomial of weights 3 reads 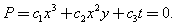
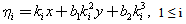
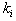 ’s 1 ≤ i ≤ N, are arbitrary constants but
’s 1 ≤ i ≤ N, are arbitrary constants but 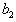 and
and 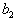 are constant to be determined. This way a direct computation tells us that the corresponding Hirota bilinear equation
are constant to be determined. This way a direct computation tells us that the corresponding Hirota bilinear equation 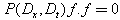 possesses the N-wave solution.
possesses the N-wave solution.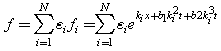
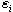 ’s and
’s and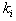 ’s are arbitrary but
’s are arbitrary but 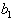 and
and 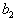 satisfy
satisfy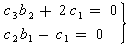
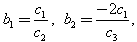 Examples with N-wave not satisfying the dispersion relationWeights
Examples with N-wave not satisfying the dispersion relationWeights 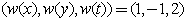 Let us finally introduce the weights of independent variables Weights
Let us finally introduce the weights of independent variables Weights 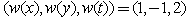 Then, the homogenous polynomial of weights 2 reads
Then, the homogenous polynomial of weights 2 reads 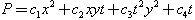
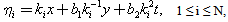
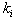 are arbitrary but
are arbitrary but 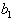 and
and 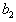 are constants to be determined.Now a similar direct computation tells that the corresponding Hirota bilinear equation
are constants to be determined.Now a similar direct computation tells that the corresponding Hirota bilinear equation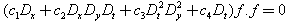
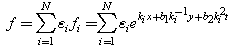
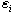 ’s and
’s and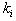 ’s are arbitrary but
’s are arbitrary but 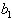 and
and 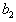 satisfy
satisfy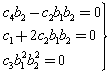
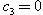 tells that the Hirota bilinear equation
tells that the Hirota bilinear equation 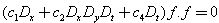
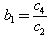 and
and 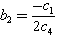 Example 2. weights
Example 2. weights 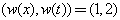 Let us first introduce the weights of independent variables
Let us first introduce the weights of independent variables 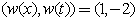 Then general homogenous polynomials of weights 1 is
Then general homogenous polynomials of weights 1 is 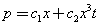
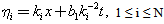
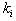 ’s are arbitrary constants but
’s are arbitrary constants but 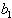 is a constant to be determined.Now, a similar direct computation tells that the corresponding Hirota bilinear equation
is a constant to be determined.Now, a similar direct computation tells that the corresponding Hirota bilinear equation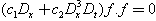
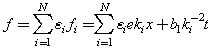
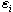 ’s and
’s and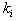 ’s are arbitrary but
’s are arbitrary but 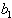 satisfy
satisfy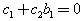 With
With 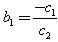 .
. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML