A. Ndanusa, K. R. Adeboye
Department of Mathematics and Statistics, Federal University of Technology, Minna, Nigeria
Correspondence to: A. Ndanusa, Department of Mathematics and Statistics, Federal University of Technology, Minna, Nigeria.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
A preconditioner of the type 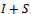 for speeding up convergence of the successive overrelaxation (SOR) iterative method for solving linear system
for speeding up convergence of the successive overrelaxation (SOR) iterative method for solving linear system 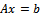 is proposed. Two forms of the preconditioned SOR iteration are obtained and implemented, under limited conditions imposed on the coefficient matrix of the original linear system. Convergence properties are analyzed and established in conformity with standard procedures. The rates of convergence of the preconditioned iterations are shown to supersede that of the SOR method. Numerical experiments confirmed the established theoretical results.
is proposed. Two forms of the preconditioned SOR iteration are obtained and implemented, under limited conditions imposed on the coefficient matrix of the original linear system. Convergence properties are analyzed and established in conformity with standard procedures. The rates of convergence of the preconditioned iterations are shown to supersede that of the SOR method. Numerical experiments confirmed the established theoretical results.
Keywords:
Spectral Radius, Preconditioner, Iterative Matrix, Linear System, L-martices
Cite this paper:
A. Ndanusa, K. R. Adeboye, "Preconditioned SOR Iterative Methods for L-martices", American Journal of Computational and Applied Mathematics, Vol. 2 No. 6, 2012, pp. 300-305. doi: 10.5923/j.ajcam.20120206.08.
1. Introduction
Suppose the linear system of equations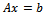 | (1) |
is such that 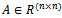 is an
is an 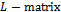 ,
, 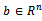 is the right-hand side vector, and
is the right-hand side vector, and 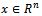 is the vector of unknown. All the numerical methods for solution of a linear system can be categorised into two thus; direct and iterative methods.A direct method is one that produces the exact solution of a linear system by performing a prescribed, finite number of operations (steps), if there were no round-off error. Examples of direct methods for solving linear systems include, graphical method, matrix inversion method, Cramer’s rule, elimination of unknowns, Gaussian elimination and LU decomposition. However, because direct methods are mostly restricted to small systems of linear equations, iterative methods remain the dominating and preferred techniques for solving very large linear systems.An iterative method for solving a linear system consists of a process whereby the system
is the vector of unknown. All the numerical methods for solution of a linear system can be categorised into two thus; direct and iterative methods.A direct method is one that produces the exact solution of a linear system by performing a prescribed, finite number of operations (steps), if there were no round-off error. Examples of direct methods for solving linear systems include, graphical method, matrix inversion method, Cramer’s rule, elimination of unknowns, Gaussian elimination and LU decomposition. However, because direct methods are mostly restricted to small systems of linear equations, iterative methods remain the dominating and preferred techniques for solving very large linear systems.An iterative method for solving a linear system consists of a process whereby the system 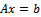 is converted into an equivalent system of the form
is converted into an equivalent system of the form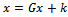 | (2) |
What follows next is application of the general linear iteration formula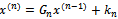 | (3) |
where 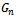 , referred to as the Iteration matrix, is a matrix depending upon A and x, and
, referred to as the Iteration matrix, is a matrix depending upon A and x, and 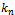 is a column vector. At each step of the iteration a solution vector,
is a column vector. At each step of the iteration a solution vector, 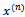 , that more accurately approximates the solution to the linear system than its predecessor, is produced. This sequence
, that more accurately approximates the solution to the linear system than its predecessor, is produced. This sequence 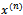 should be so defined that
should be so defined that 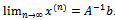 . For any iteration to be convergent, the spectral radius of the iteration matrix must be less than 1[1].Iterative methods are further classified into two main types, namely, stationary and nonstationary iterative methods. Stationary iterative methods are those methods that can be expressed in the form
. For any iteration to be convergent, the spectral radius of the iteration matrix must be less than 1[1].Iterative methods are further classified into two main types, namely, stationary and nonstationary iterative methods. Stationary iterative methods are those methods that can be expressed in the form 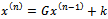 | (4) |
where neither G nor k depend upon the iteration count n[2]. Stationary methods are simpler to implement and understood compared to nonstationary methods. However, they are usually not effective when used alone; hence the need to implement them along with preconditioners.If we assume that 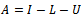 , where
, where 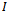 is the identity matrix,
is the identity matrix, 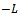 the strictly lower triangular part of A, and
the strictly lower triangular part of A, and 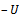 the strictly upper triangular part of A, then the successive overrelaxation method as invented by[3] has the following matrix from
the strictly upper triangular part of A, then the successive overrelaxation method as invented by[3] has the following matrix from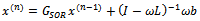 | (5) |
where 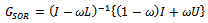 is the SOR iteration matrix. Various authors have introduced preconditioners for accelerating the convergence of the SOR method[4 -9].
is the SOR iteration matrix. Various authors have introduced preconditioners for accelerating the convergence of the SOR method[4 -9].
2. Materials and Methods
Consider the preconditioner 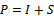 , where
, where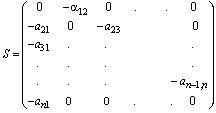 | (6) |
The above preconditioning matrix is applied to the coefficient matrix A of system (1) thus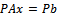 | (7) |
which results into the equivalent preconditioned system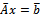 | (8) |
where 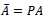 and
and 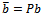 . The preconditioned coefficient matrix
. The preconditioned coefficient matrix 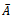 is further analyzed as follows.
is further analyzed as follows.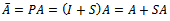 | (9) |
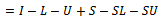 | (10) |
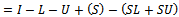 | (11) |
Further splittings of the bracket terms in (11) are obtained as follows.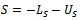 | (12) |
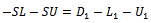 | (13) |
Thus 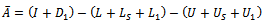 | (14) |
or equivalently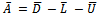 | (15) |
where 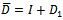 is the diagonal,
is the diagonal, 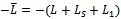 and
and 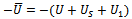 are strictly lower and strictly upper triangular parts of
are strictly lower and strictly upper triangular parts of 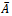 respectively.The application of overrelaxation parameter
respectively.The application of overrelaxation parameter 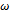 to the preconditioned linear system (8) yields
to the preconditioned linear system (8) yields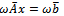 | (16) |
where,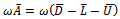 | (17) |
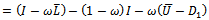 | (18) |
Thus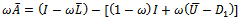 | (19) |
is a regular splitting of 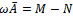 , where
, where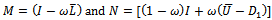 | (20) |
Hence, the following preconditioned SOR iterative scheme is obtained.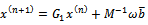 | (21) |
And the preconditioned SOR iterative matrix 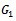 has the representation
has the representation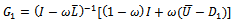 | (22) |
Similarly,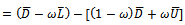 | (23) |
is another splitting of the the preconditioned coefficient matrix 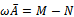 , with
, with 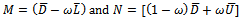 | (24) |
And this leads to the second preconditioned SOR iterative scheme 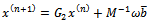 | (25) |
with the second preconditioned iterative matrix 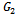 having the representation
having the representation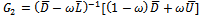 | (26) |
3. Convergence Analysis
Convergence of the preconditioned iterative schemes (21) and (25) is established by showing that the spectral radii of the 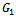 and
and 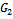 are less than 1 in each case.Lemma 3.1 (Varga[10] ): Let
are less than 1 in each case.Lemma 3.1 (Varga[10] ): Let 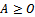 be an irreducible
be an irreducible 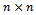 matrix. Then,i.
matrix. Then,i. 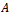 has a positive real eigenvalue equal to its spectral radius.ii. To
has a positive real eigenvalue equal to its spectral radius.ii. To 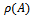 there corresponds an eigenvector
there corresponds an eigenvector 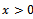 .iii.
.iii. 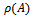 increases when any entry of
increases when any entry of 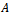 increases.iv.
increases.iv. 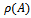 is a simple eigenvalue of
is a simple eigenvalue of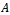 .Lemma 3.2 (Varga[10] ): Let
.Lemma 3.2 (Varga[10] ): Let 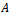 be a nonnegative matrix. Theni. If
be a nonnegative matrix. Theni. If 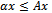 for some nonnegative vector
for some nonnegative vector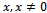 , then
, then 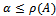 .ii. If
.ii. If 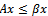 for some positive vector x, then
for some positive vector x, then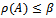 . Moreover, if
. Moreover, if 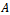 is irreducible and if
is irreducible and if 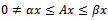 for some nonnegative vector x, then
for some nonnegative vector x, then 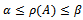 and x is a positive vector. Lemma 3.1 (Li and Sun[11] ): Let
and x is a positive vector. Lemma 3.1 (Li and Sun[11] ): Let 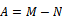 be an
be an 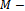 splitting of
splitting of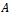 . Then the splitting is convergent, i.e.,
. Then the splitting is convergent, i.e., 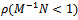 , if and only if
, if and only if 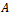 is a nonsingular
is a nonsingular 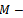 matrix.By employing the foregoing lemmas (lemmas 3.1 - 3.3), the next three theorems are proposed to establish convergence of the preconditioned iterative methods.Theorem 3.1: Let
matrix.By employing the foregoing lemmas (lemmas 3.1 - 3.3), the next three theorems are proposed to establish convergence of the preconditioned iterative methods.Theorem 3.1: Let 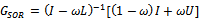 be the SOR iteration matrix while
be the SOR iteration matrix while 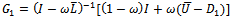 and
and 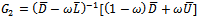 be the preconditioned SOR iteration matrices. If
be the preconditioned SOR iteration matrices. If 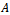 is an irreducible
is an irreducible 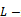 matrix with
matrix with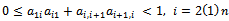 , and
, and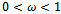 , then
, then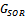 ,
, 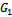 and
and 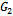 are nonnegative and irreducible matrices.Proof Since
are nonnegative and irreducible matrices.Proof Since 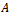 is an
is an 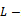 matrix,
matrix, 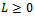 and
and 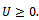 Now,
Now, 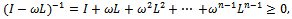
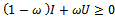 , for
, for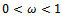 . Thus
. Thus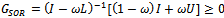 . Hence,
. Hence, 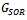 is a nonnegative matrix. One can also obtain that for
is a nonnegative matrix. One can also obtain that for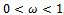 ,
,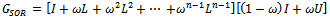 | (27) |
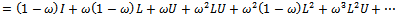 | (28) |
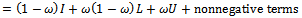 | (29) |
Since 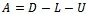 is irreducible, so also is
is irreducible, so also is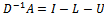 , because it inherits the nonzero structure of the irreducible matrix
, because it inherits the nonzero structure of the irreducible matrix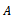 . The same thing applies to the matrix
. The same thing applies to the matrix 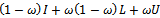 since the coefficients of
since the coefficients of 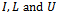 are different from zero and less than 1 in absolute value. Hence,
are different from zero and less than 1 in absolute value. Hence, 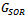 is an irreducible matrix.
is an irreducible matrix.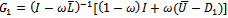 | (30) |
Since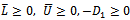 , for
, for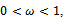
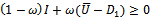 and
and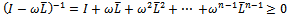 . Consequently, one can find that
. Consequently, one can find that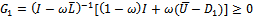 . Hence
. Hence  is a nonnegative matrix.Now,
is a nonnegative matrix.Now,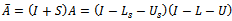 | (31) |
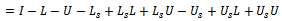 | (32) |
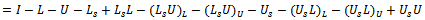 | (33) |
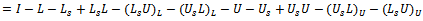 | (34) |
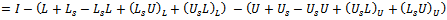 | (35) |
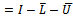 | (36) |
where 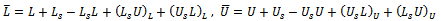 and
and 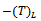 and
and 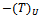 denote the strictly lower and strictly upper parts of the matrix
denote the strictly lower and strictly upper parts of the matrix 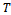 respectively.
respectively. 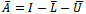 is irreducible, since it inherits the nonzero structure of the irreducible matrix
is irreducible, since it inherits the nonzero structure of the irreducible matrix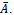 Now,
Now,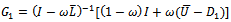 | (37) |
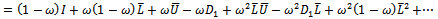 | (38) |
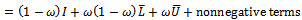 | (39) |
The matrix 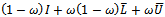 is irreducible, since the coefficients of
is irreducible, since the coefficients of 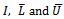 are different from zero and less than one in absolute value. Therefore, the matrix
are different from zero and less than one in absolute value. Therefore, the matrix 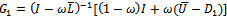 is irreducible. Hence
is irreducible. Hence 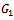 is a nonnegative and irreducible matrix.Similarly, consider
is a nonnegative and irreducible matrix.Similarly, consider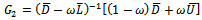 | (40) |
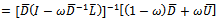 | (41) |
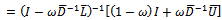 | (42) |
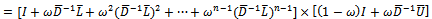 | (43) |
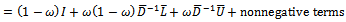 | (44) |
Using similar arguments it is conclusive that 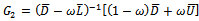 is a nonnegative and irreducible matrix. The proof is completed.Theorem 3.2: Let
is a nonnegative and irreducible matrix. The proof is completed.Theorem 3.2: Let 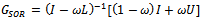 and
and 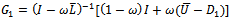 be the SOR and preconditioned SOR iteration matrices respectively. If
be the SOR and preconditioned SOR iteration matrices respectively. If 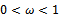 and if
and if 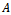 is an irreducible
is an irreducible 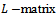 with
with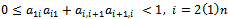 . Then,(i)
. Then,(i) 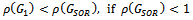 (ii)
(ii) 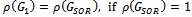 (iii)
(iii) 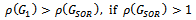 ProofFrom Theorem 3.1,
ProofFrom Theorem 3.1, 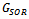 and
and 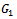 are nonnegative and irreducible matrices. Suppose
are nonnegative and irreducible matrices. Suppose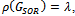 then there exists a positive vector
then there exists a positive vector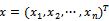 , such that
, such that 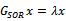 | (45) |
That is,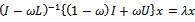 | (46) |
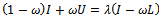 | (47) |
Therefore, for this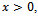
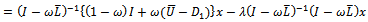 | (48) |
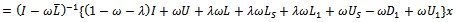 | (49) |
From equation (47)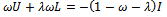 | (50) |
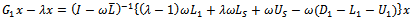 | (51) |
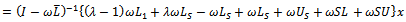 | (52) |
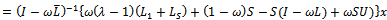 | (53) |
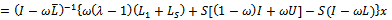 | (54) |
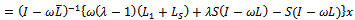 | (55) |
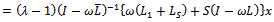 | (56) |
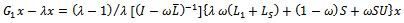 | (57) |
Let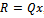 , where
, where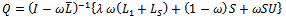 . Then
. Then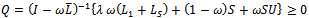 , because
, because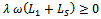 ,
, . Also,
. Also, 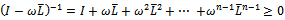 , since
, since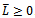 . Therefore,
. Therefore, 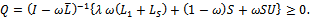 So,
So, 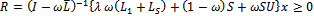 , since
, since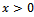 .i. If
.i. If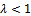 , then
, then 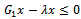 but not equal to 0.Therefore,
but not equal to 0.Therefore,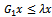 | (58) |
From Lemma 3.2, one obtains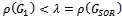 | (59) |
ii. If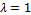 , then
, then 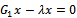 Therefore,
Therefore,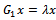 | (60) |
From Lemma 3.2, we have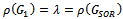 | (61) |
iii. If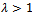 , then
, then 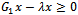 but not equal to 0.Therefore,
but not equal to 0.Therefore,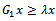 | (62) |
From Lemma 3.2, we have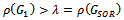 | (63) |
The proof is completed. Theorem 3.3: Let 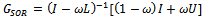 and
and 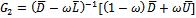 be the SOR and the preconditioned SOR iteration matrices respectively. If
be the SOR and the preconditioned SOR iteration matrices respectively. If 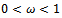 and if
and if 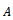 is an irreducible
is an irreducible 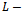 matrix with
matrix with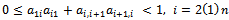 . Then,(i)
. Then,(i) 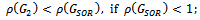 (ii)
(ii) 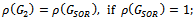 (iii)
(iii) 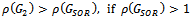 ProofFrom Theorem 3.1,
ProofFrom Theorem 3.1, 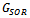 and
and 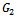 are nonnegative and irreducible matrices. Suppose
are nonnegative and irreducible matrices. Suppose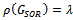 , then there exists a positive vector
, then there exists a positive vector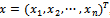 , such that
, such that 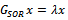 | (64) |
That is,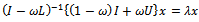 | (65) |
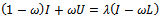 | (66) |
Therefore, for this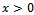 ,
,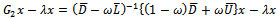 | (67) |
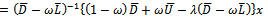 | (68) |
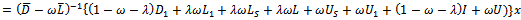 | (69) |
From equation (66)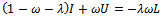 | (70) |
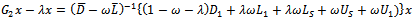 | (71) |
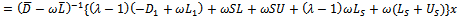 | (72) |
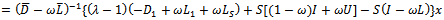 | (73) |
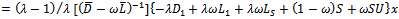 | (74) |
Let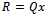 , with
, with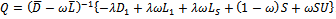 . It is clear that
. It is clear that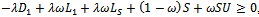 , since
, since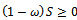 ,
, 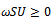 ,
,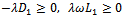 and
and 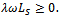 Since
Since 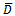 is a nonsingular matrix, we let
is a nonsingular matrix, we let 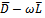 be a splitting of some matrix
be a splitting of some matrix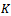 , i.e.,
, i.e., 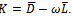 Also,
Also, 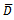 is an
is an 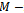 matrix and
matrix and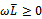 . Thus,
. Thus, 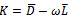 is an
is an 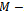 splitting. Now,
splitting. Now, 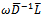 is a strictly lower triangular matrix, and by implication its eigenvalues lie on its main diagonal; in this case they are all zeros. Therefore,
is a strictly lower triangular matrix, and by implication its eigenvalues lie on its main diagonal; in this case they are all zeros. Therefore, 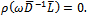 since
since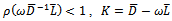 is a convergent splitting. By the foregoing,
is a convergent splitting. By the foregoing, 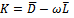 is an
is an 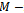 splitting and
splitting and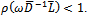 . Lemma 3.3 is invoked in order to establish that
. Lemma 3.3 is invoked in order to establish that 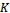 is an
is an 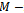 matrix. Since K is an
matrix. Since K is an 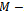 matrix, by definition,
matrix, by definition, 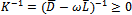 . Thus,
. Thus, 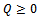 and
and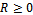 .If
.If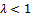 , then
, then 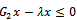 but not equal to 0.Therefore,
but not equal to 0.Therefore,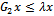 | (75) |
From Lemma 3.2, we have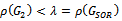 | (76) |
ii. If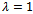 , then
, then 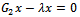 Therefore,
Therefore,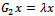 | (77) |
From Lemma 3.2, we have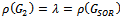 | (78) |
iii. If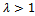 , then
, then 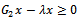 but not equal to 0.Therefore,
but not equal to 0.Therefore,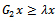 | (79) |
From Lemma 3.2, we have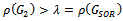 | (80) |
The proof is completed.If in 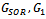 and
and 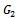 the relaxation parameter
the relaxation parameter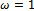 , the iteration matrices of the Gauss-Seidel method results in each case. Therefore, the following corollaries are direct implications of Theorem 3.1 and Theorem 3.2.Corollary 3.1 Let
, the iteration matrices of the Gauss-Seidel method results in each case. Therefore, the following corollaries are direct implications of Theorem 3.1 and Theorem 3.2.Corollary 3.1 Let 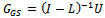 be the Gauss-Seidel iteration matrix and
be the Gauss-Seidel iteration matrix and 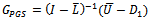 be the preconditioned Gauss-Seidel iteration matrix. If
be the preconditioned Gauss-Seidel iteration matrix. If 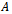 is an irreducible
is an irreducible 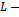 matrix with
matrix with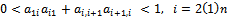 , then(i)
, then(i) 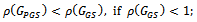 (ii)
(ii) 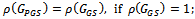 (iii)
(iii) 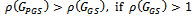 Corollary 3.2 Let
Corollary 3.2 Let 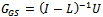 be the Gauss-Seidel iteration matrix and
be the Gauss-Seidel iteration matrix and 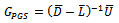 be the preconditioned Gauss-Seidel iteration matrix. If
be the preconditioned Gauss-Seidel iteration matrix. If 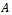 is an irreducible
is an irreducible 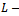 matrix with
matrix with 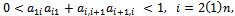 then(i)
then(i) 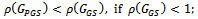 (ii)
(ii) 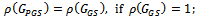 (iii)
(iii) 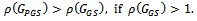
4. Numerical Experiments
Example 4.1 Consider a 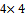 matrix of the form.
matrix of the form. Table 1 displays the results of comparing the spectral radius es of
Table 1 displays the results of comparing the spectral radius es of 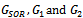 iterative matrices corresponding to the matrix in example 4.1.Table 1 compares the spectral radiuses of
iterative matrices corresponding to the matrix in example 4.1.Table 1 compares the spectral radiuses of 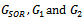 iteration matrices. It reveals that the two preconditioned SOR iteration matrices exhibit faster convergence than the SOR, because the spectral radiuses of
iteration matrices. It reveals that the two preconditioned SOR iteration matrices exhibit faster convergence than the SOR, because the spectral radiuses of 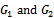 are less than the spectral radius of
are less than the spectral radius of 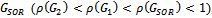 , for all values of relaxation parameter
, for all values of relaxation parameter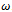 .Example 4.2 Consider a
.Example 4.2 Consider a 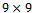 matrix of the form.
matrix of the form.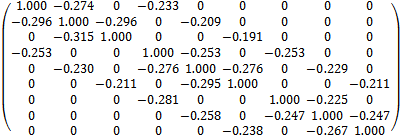 The results of example 4.2 are displayed in Table 2 as follows.
The results of example 4.2 are displayed in Table 2 as follows.Table 1. Result of Spectral Radiuses of
 , ,
 and and
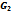 Iterative Matrices for Example 4.1 Iterative Matrices for Example 4.1
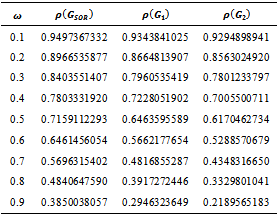 |
| |
|
Table 2. Result of Spectral Radiuses of
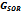 , ,
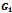 and and
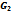 Iterative Matrices for Example 4.2 Iterative Matrices for Example 4.2
 |
| |
|
Table 2 goes further to confirm the efficiency of the preconditioned iterations by revealing that the spectral radiuses of the preconditioned iterative matrices  are less than the spectral radius of the SOR iterative matrix
are less than the spectral radius of the SOR iterative matrix . That is,
. That is, 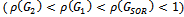 , for all values of relaxation parameter
, for all values of relaxation parameter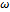 .
.
5. Conclusions
In this research work, a preconditioning matrix is introduced. Two different forms of the preconditioned SOR-type iterations are formulated for the preconditioner. Some theorems are proposed and proven in order to establish the validity and efficiency of the preconditioned iterations. The preconditioned iterations are shown to satisfy standard convergence criteria under mild conditions imposed on the coefficient matrix of the linear system. Based on the results obtained, it is instructive to conclude that the preconditioned SOR iterative methods presented in this research work provide better and faster convergence properties than the SOR.
ACKNOWLEDGEMENTS
The authors would like express their indebtedness to all those whose works were cited in this paper, and all others who were not cited, but nevertheless contributed in various capacities toward the success of this work. The authors remain grateful.
References
| [1] | William F. Ames, Numerical methods for partial differential equations, 2nd ed., Thomas Nelson & Sons Ltd, Great Britain, 1977. |
| [2] | Richard Barrett, Michael Berry, Tony F. Chan, James Demmel, June M. Donato, Jack Dongarra, Victor Eijkhout, Roldan Pozo, Charles Romine, Henk Van der Vorst, Templates for the solution of linear systems: Building blocks for iterative methods, SIAM, Philadelphia, PA, 1994. |
| [3] | David M. Young “Iterative methods for solving partial difference equations of elliptic type”, Doctoral Thesis, Harvard University, Cambridge, 1950. |
| [4] | Mehdi Dehghan, Masoud Hajarian, “Improving Preconditioned SOR-Type Iterative Methods for L-martices”, International Journal for Numerical Methods in Biomedical Engineering, no.27, pp.774-784, 2011. |
| [5] | Abdulrahman Ndanusa, “Preconditioned successive overrelaxation iterative method for solving partial differential equations of elliptic type”, Doctoral Thesis, Federal University of Technology, Minna, Nigeria, 2012. |
| [6] | Shi-Liang Wu, Cui-Xia Li, Ting-Zhu Huang, “Improvements of Preconditioned SOR Iterative Methods for L-martices”, WSEAS Transactions on Mathematics, vol.12, no.9, 2010. |
| [7] | D. J. Evans, M. M. Martins, M. E. Trigo, “The AOR iterative method for new preconditioned linear systems”, Elsevier Science, Journal of Computational and Applied Mathematics”, no.132, pp. 461-466, 2001. |
| [8] | Hongjuan Wang, Yao-tang Li, “A new preconditioned AOR iterative method for L-martices”, Elsevier Science, Journal of Computational and Applied Mathematics”, no.229, pp. 47-53, 2009. |
| [9] | Davod Khojasteh Salkuyeh, Yousef Abdolalizadeh, “On the preconditioning of the AOR iterative methods for M-martices”, International Journal of Applied Mathematics and Computation, vol.3, no.2, 2011. |
| [10] | Richard S. Varga, Matrix iterative analysis, 2nd ed., Prentice-Hall, Englewood Cliffs, New Jersey, USA, 1981. |
| [11] | Wen Li, Weiwei Sun, “Modified Gauss-Seidel type methods and Jacobi type methods for Z-martices”, Elsevier Science, Linear Algebra and its Applications, no.317, pp.227-240, 2000. |

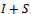 for speeding up convergence of the successive overrelaxation (SOR) iterative method for solving linear system
for speeding up convergence of the successive overrelaxation (SOR) iterative method for solving linear system 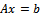 is proposed. Two forms of the preconditioned SOR iteration are obtained and implemented, under limited conditions imposed on the coefficient matrix of the original linear system. Convergence properties are analyzed and established in conformity with standard procedures. The rates of convergence of the preconditioned iterations are shown to supersede that of the SOR method. Numerical experiments confirmed the established theoretical results.
is proposed. Two forms of the preconditioned SOR iteration are obtained and implemented, under limited conditions imposed on the coefficient matrix of the original linear system. Convergence properties are analyzed and established in conformity with standard procedures. The rates of convergence of the preconditioned iterations are shown to supersede that of the SOR method. Numerical experiments confirmed the established theoretical results.
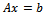
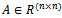 is an
is an 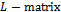 ,
, 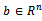 is the right-hand side vector, and
is the right-hand side vector, and 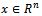 is the vector of unknown. All the numerical methods for solution of a linear system can be categorised into two thus; direct and iterative methods.A direct method is one that produces the exact solution of a linear system by performing a prescribed, finite number of operations (steps), if there were no round-off error. Examples of direct methods for solving linear systems include, graphical method, matrix inversion method, Cramer’s rule, elimination of unknowns, Gaussian elimination and LU decomposition. However, because direct methods are mostly restricted to small systems of linear equations, iterative methods remain the dominating and preferred techniques for solving very large linear systems.An iterative method for solving a linear system consists of a process whereby the system
is the vector of unknown. All the numerical methods for solution of a linear system can be categorised into two thus; direct and iterative methods.A direct method is one that produces the exact solution of a linear system by performing a prescribed, finite number of operations (steps), if there were no round-off error. Examples of direct methods for solving linear systems include, graphical method, matrix inversion method, Cramer’s rule, elimination of unknowns, Gaussian elimination and LU decomposition. However, because direct methods are mostly restricted to small systems of linear equations, iterative methods remain the dominating and preferred techniques for solving very large linear systems.An iterative method for solving a linear system consists of a process whereby the system 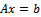 is converted into an equivalent system of the form
is converted into an equivalent system of the form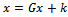
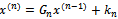
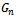 , referred to as the Iteration matrix, is a matrix depending upon A and x, and
, referred to as the Iteration matrix, is a matrix depending upon A and x, and 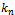 is a column vector. At each step of the iteration a solution vector,
is a column vector. At each step of the iteration a solution vector, 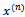 , that more accurately approximates the solution to the linear system than its predecessor, is produced. This sequence
, that more accurately approximates the solution to the linear system than its predecessor, is produced. This sequence 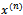 should be so defined that
should be so defined that 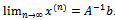 . For any iteration to be convergent, the spectral radius of the iteration matrix must be less than 1[1].Iterative methods are further classified into two main types, namely, stationary and nonstationary iterative methods. Stationary iterative methods are those methods that can be expressed in the form
. For any iteration to be convergent, the spectral radius of the iteration matrix must be less than 1[1].Iterative methods are further classified into two main types, namely, stationary and nonstationary iterative methods. Stationary iterative methods are those methods that can be expressed in the form 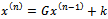
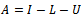 , where
, where 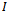 is the identity matrix,
is the identity matrix, 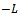 the strictly lower triangular part of A, and
the strictly lower triangular part of A, and 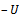 the strictly upper triangular part of A, then the successive overrelaxation method as invented by[3] has the following matrix from
the strictly upper triangular part of A, then the successive overrelaxation method as invented by[3] has the following matrix from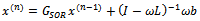
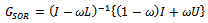 is the SOR iteration matrix. Various authors have introduced preconditioners for accelerating the convergence of the SOR method[4 -9].
is the SOR iteration matrix. Various authors have introduced preconditioners for accelerating the convergence of the SOR method[4 -9].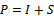 , where
, where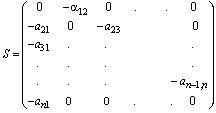
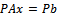
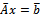
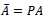 and
and 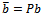 . The preconditioned coefficient matrix
. The preconditioned coefficient matrix 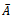 is further analyzed as follows.
is further analyzed as follows.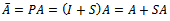
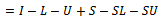
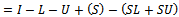
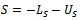
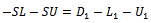
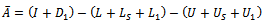
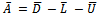
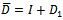 is the diagonal,
is the diagonal, 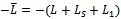 and
and 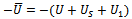 are strictly lower and strictly upper triangular parts of
are strictly lower and strictly upper triangular parts of 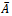 respectively.The application of overrelaxation parameter
respectively.The application of overrelaxation parameter 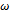 to the preconditioned linear system (8) yields
to the preconditioned linear system (8) yields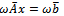
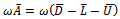
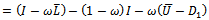
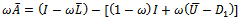
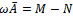 , where
, where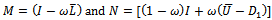
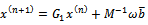
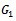 has the representation
has the representation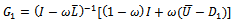
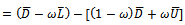
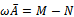 , with
, with 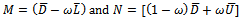
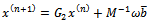
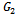 having the representation
having the representation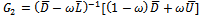
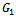 and
and 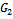 are less than 1 in each case.Lemma 3.1 (Varga[10] ): Let
are less than 1 in each case.Lemma 3.1 (Varga[10] ): Let 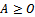 be an irreducible
be an irreducible 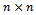 matrix. Then,i.
matrix. Then,i. 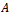 has a positive real eigenvalue equal to its spectral radius.ii. To
has a positive real eigenvalue equal to its spectral radius.ii. To 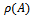 there corresponds an eigenvector
there corresponds an eigenvector 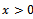 .iii.
.iii. 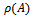 increases when any entry of
increases when any entry of 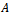 increases.iv.
increases.iv. 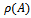 is a simple eigenvalue of
is a simple eigenvalue of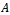 .Lemma 3.2 (Varga[10] ): Let
.Lemma 3.2 (Varga[10] ): Let 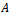 be a nonnegative matrix. Theni. If
be a nonnegative matrix. Theni. If 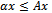 for some nonnegative vector
for some nonnegative vector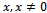 , then
, then 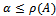 .ii. If
.ii. If 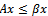 for some positive vector x, then
for some positive vector x, then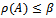 . Moreover, if
. Moreover, if 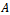 is irreducible and if
is irreducible and if 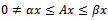 for some nonnegative vector x, then
for some nonnegative vector x, then 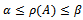 and x is a positive vector. Lemma 3.1 (Li and Sun[11] ): Let
and x is a positive vector. Lemma 3.1 (Li and Sun[11] ): Let 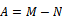 be an
be an 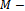 splitting of
splitting of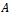 . Then the splitting is convergent, i.e.,
. Then the splitting is convergent, i.e., 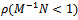 , if and only if
, if and only if 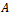 is a nonsingular
is a nonsingular 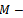 matrix.By employing the foregoing lemmas (lemmas 3.1 - 3.3), the next three theorems are proposed to establish convergence of the preconditioned iterative methods.Theorem 3.1: Let
matrix.By employing the foregoing lemmas (lemmas 3.1 - 3.3), the next three theorems are proposed to establish convergence of the preconditioned iterative methods.Theorem 3.1: Let 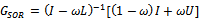 be the SOR iteration matrix while
be the SOR iteration matrix while 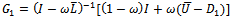 and
and 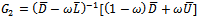 be the preconditioned SOR iteration matrices. If
be the preconditioned SOR iteration matrices. If 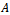 is an irreducible
is an irreducible 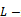 matrix with
matrix with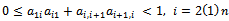 , and
, and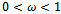 , then
, then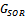 ,
, 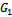 and
and 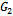 are nonnegative and irreducible matrices.Proof Since
are nonnegative and irreducible matrices.Proof Since 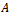 is an
is an 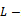 matrix,
matrix, 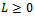 and
and 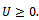 Now,
Now, 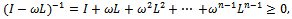
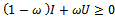 , for
, for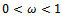 . Thus
. Thus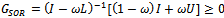 . Hence,
. Hence, 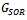 is a nonnegative matrix. One can also obtain that for
is a nonnegative matrix. One can also obtain that for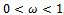 ,
,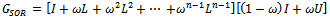
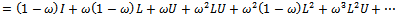
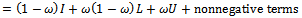
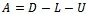 is irreducible, so also is
is irreducible, so also is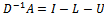 , because it inherits the nonzero structure of the irreducible matrix
, because it inherits the nonzero structure of the irreducible matrix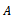 . The same thing applies to the matrix
. The same thing applies to the matrix 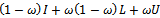 since the coefficients of
since the coefficients of 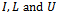 are different from zero and less than 1 in absolute value. Hence,
are different from zero and less than 1 in absolute value. Hence, 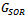 is an irreducible matrix.
is an irreducible matrix.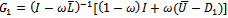
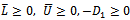 , for
, for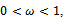
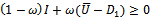 and
and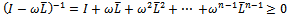 . Consequently, one can find that
. Consequently, one can find that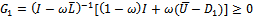 . Hence
. Hence  is a nonnegative matrix.Now,
is a nonnegative matrix.Now,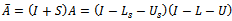
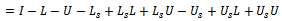
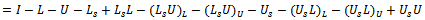
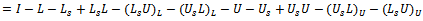
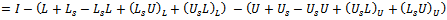
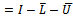
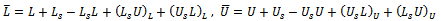 and
and 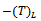 and
and 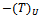 denote the strictly lower and strictly upper parts of the matrix
denote the strictly lower and strictly upper parts of the matrix 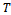 respectively.
respectively. 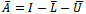 is irreducible, since it inherits the nonzero structure of the irreducible matrix
is irreducible, since it inherits the nonzero structure of the irreducible matrix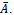 Now,
Now,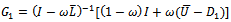
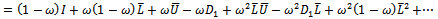
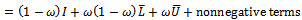
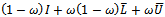 is irreducible, since the coefficients of
is irreducible, since the coefficients of 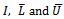 are different from zero and less than one in absolute value. Therefore, the matrix
are different from zero and less than one in absolute value. Therefore, the matrix 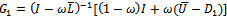 is irreducible. Hence
is irreducible. Hence 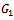 is a nonnegative and irreducible matrix.Similarly, consider
is a nonnegative and irreducible matrix.Similarly, consider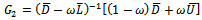
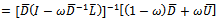
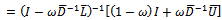
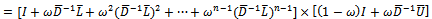
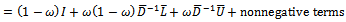
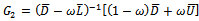 is a nonnegative and irreducible matrix. The proof is completed.Theorem 3.2: Let
is a nonnegative and irreducible matrix. The proof is completed.Theorem 3.2: Let 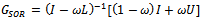 and
and 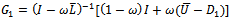 be the SOR and preconditioned SOR iteration matrices respectively. If
be the SOR and preconditioned SOR iteration matrices respectively. If 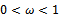 and if
and if 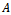 is an irreducible
is an irreducible 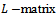 with
with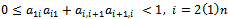 . Then,(i)
. Then,(i) 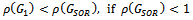 (ii)
(ii) 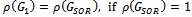 (iii)
(iii) 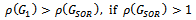 ProofFrom Theorem 3.1,
ProofFrom Theorem 3.1, 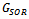 and
and 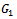 are nonnegative and irreducible matrices. Suppose
are nonnegative and irreducible matrices. Suppose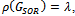 then there exists a positive vector
then there exists a positive vector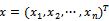 , such that
, such that 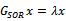
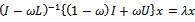
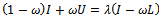
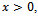
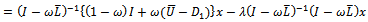
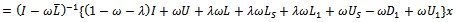
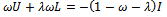
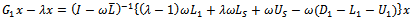
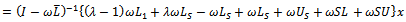
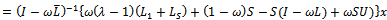
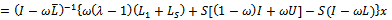
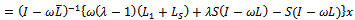
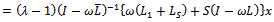
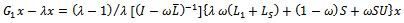
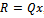 , where
, where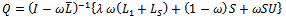 . Then
. Then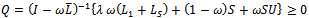 , because
, because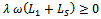 ,
, . Also,
. Also, 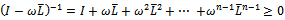 , since
, since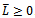 . Therefore,
. Therefore, 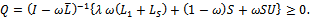 So,
So, 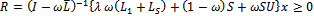 , since
, since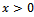 .i. If
.i. If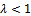 , then
, then 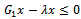 but not equal to 0.Therefore,
but not equal to 0.Therefore,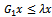
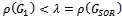
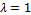 , then
, then 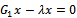 Therefore,
Therefore,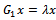
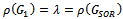
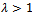 , then
, then 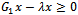 but not equal to 0.Therefore,
but not equal to 0.Therefore,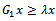
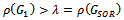
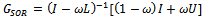 and
and 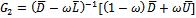 be the SOR and the preconditioned SOR iteration matrices respectively. If
be the SOR and the preconditioned SOR iteration matrices respectively. If 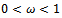 and if
and if 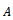 is an irreducible
is an irreducible 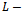 matrix with
matrix with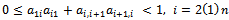 . Then,(i)
. Then,(i) 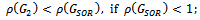 (ii)
(ii) 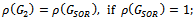 (iii)
(iii) 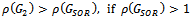 ProofFrom Theorem 3.1,
ProofFrom Theorem 3.1, 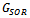 and
and 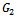 are nonnegative and irreducible matrices. Suppose
are nonnegative and irreducible matrices. Suppose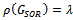 , then there exists a positive vector
, then there exists a positive vector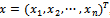 , such that
, such that 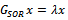
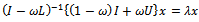
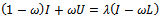
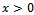 ,
,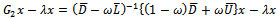
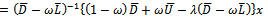
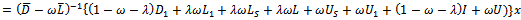
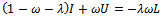
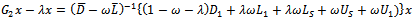
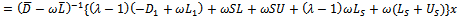
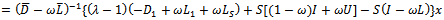
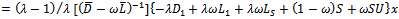
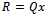 , with
, with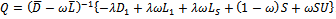 . It is clear that
. It is clear that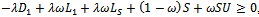 , since
, since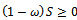 ,
, 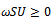 ,
,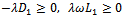 and
and 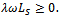 Since
Since 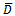 is a nonsingular matrix, we let
is a nonsingular matrix, we let 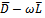 be a splitting of some matrix
be a splitting of some matrix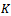 , i.e.,
, i.e., 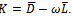 Also,
Also, 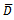 is an
is an 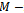 matrix and
matrix and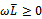 . Thus,
. Thus, 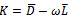 is an
is an 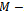 splitting. Now,
splitting. Now, 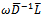 is a strictly lower triangular matrix, and by implication its eigenvalues lie on its main diagonal; in this case they are all zeros. Therefore,
is a strictly lower triangular matrix, and by implication its eigenvalues lie on its main diagonal; in this case they are all zeros. Therefore, 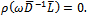 since
since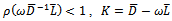 is a convergent splitting. By the foregoing,
is a convergent splitting. By the foregoing, 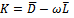 is an
is an 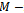 splitting and
splitting and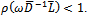 . Lemma 3.3 is invoked in order to establish that
. Lemma 3.3 is invoked in order to establish that 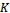 is an
is an 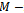 matrix. Since K is an
matrix. Since K is an 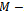 matrix, by definition,
matrix, by definition, 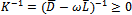 . Thus,
. Thus, 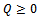 and
and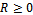 .If
.If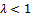 , then
, then 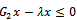 but not equal to 0.Therefore,
but not equal to 0.Therefore,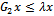
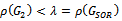
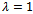 , then
, then 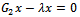 Therefore,
Therefore,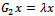
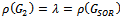
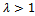 , then
, then 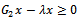 but not equal to 0.Therefore,
but not equal to 0.Therefore,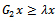
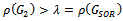
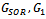 and
and 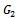 the relaxation parameter
the relaxation parameter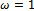 , the iteration matrices of the Gauss-Seidel method results in each case. Therefore, the following corollaries are direct implications of Theorem 3.1 and Theorem 3.2.Corollary 3.1 Let
, the iteration matrices of the Gauss-Seidel method results in each case. Therefore, the following corollaries are direct implications of Theorem 3.1 and Theorem 3.2.Corollary 3.1 Let 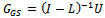 be the Gauss-Seidel iteration matrix and
be the Gauss-Seidel iteration matrix and 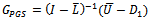 be the preconditioned Gauss-Seidel iteration matrix. If
be the preconditioned Gauss-Seidel iteration matrix. If 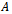 is an irreducible
is an irreducible 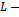 matrix with
matrix with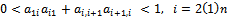 , then(i)
, then(i) 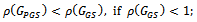 (ii)
(ii) 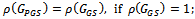 (iii)
(iii) 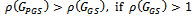 Corollary 3.2 Let
Corollary 3.2 Let 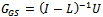 be the Gauss-Seidel iteration matrix and
be the Gauss-Seidel iteration matrix and 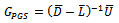 be the preconditioned Gauss-Seidel iteration matrix. If
be the preconditioned Gauss-Seidel iteration matrix. If 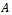 is an irreducible
is an irreducible 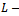 matrix with
matrix with 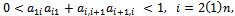 then(i)
then(i) 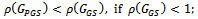 (ii)
(ii) 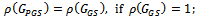 (iii)
(iii) 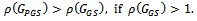
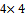 matrix of the form.
matrix of the form. Table 1 displays the results of comparing the spectral radius es of
Table 1 displays the results of comparing the spectral radius es of 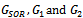 iterative matrices corresponding to the matrix in example 4.1.Table 1 compares the spectral radiuses of
iterative matrices corresponding to the matrix in example 4.1.Table 1 compares the spectral radiuses of 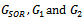 iteration matrices. It reveals that the two preconditioned SOR iteration matrices exhibit faster convergence than the SOR, because the spectral radiuses of
iteration matrices. It reveals that the two preconditioned SOR iteration matrices exhibit faster convergence than the SOR, because the spectral radiuses of 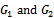 are less than the spectral radius of
are less than the spectral radius of 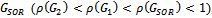 , for all values of relaxation parameter
, for all values of relaxation parameter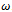 .Example 4.2 Consider a
.Example 4.2 Consider a  matrix of the form.
matrix of the form.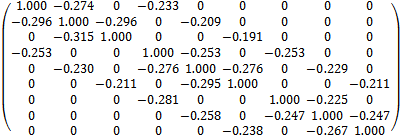 The results of example 4.2 are displayed in Table 2 as follows.
The results of example 4.2 are displayed in Table 2 as follows.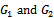 are less than the spectral radius of the SOR iterative matrix
are less than the spectral radius of the SOR iterative matrix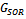 . That is,
. That is, 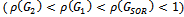 , for all values of relaxation parameter
, for all values of relaxation parameter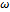 .
. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML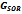 ,
, 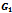 and
and 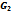 Iterative Matrices for Example 4.1
Iterative Matrices for Example 4.1
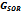 ,
, 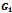 and
and 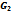 Iterative Matrices for Example 4.2
Iterative Matrices for Example 4.2