-
Paper Information
- Next Paper
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Computational and Applied Mathematics
p-ISSN: 2165-8935 e-ISSN: 2165-8943
2012; 2(6): 290-299
doi: 10.5923/j.ajcam.20120206.07
Effect of Exotic Species on a System of Native Prey-Predator Populations : A Model
O. P. Misra1, Pramod Kushwah2, Chhatrapal Singh Sikarwar1
1School of Mathematics and Allied Science, Jiwaji University, Gwalior (M.P.), 474011, India
2Govt. M.J.S.P.G. College, Bhind (M.P.), 477001, India
Correspondence to: Pramod Kushwah, Govt. M.J.S.P.G. College, Bhind (M.P.), 477001, India.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
In this paper, a mathematical model is proposed to study the effect of exotic predator population on a system of native prey-predator population. The model includes three state variables viz., density of native prey, density of native predator and density of exotic predator. The stability analysis of all the feasible equilibria are carried out and also the possibility of Hopf- bifurcation of the interior equilibrium point is investigated for the parameter 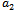 ; the predation rate of exotic predator. By varying the parameter
; the predation rate of exotic predator. By varying the parameter 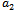 , a change in stability behaviour of the interior equilibrium is also observed. The stability and direction of bifurcating periodic solution is discussed. Finally the analytical results are supported by numerical simulation.
, a change in stability behaviour of the interior equilibrium is also observed. The stability and direction of bifurcating periodic solution is discussed. Finally the analytical results are supported by numerical simulation.
Keywords: Biological Invasion, Equilibria, Stability, Hopf-Bifurcation, Predation Rate
Cite this paper: O. P. Misra, Pramod Kushwah, Chhatrapal Singh Sikarwar, "Effect of Exotic Species on a System of Native Prey-Predator Populations : A Model", American Journal of Computational and Applied Mathematics, Vol. 2 No. 6, 2012, pp. 290-299. doi: 10.5923/j.ajcam.20120206.07.
Article Outline
1. Introduction
- The prey predator relationship still continues to be one of the main themes in mathematical ecology due to its complex dynamic behavior. Many prey predator models have been studied considering different types of functional responses [1,2,3]. It is seen that the invasion or introduction of exotic species in general disrupt the trophic dynamics of native interacting prey-predator species systems.Introduced predators usually have a dramatic effect on native prey, usually the cause of native species extinction[4, 5, 6]. The harm caused by the introduced predators is broadly known and control programs are largely identified as the best way to restore ecosystems[7]. Many authors have studied effect of exotic predator on native prey species[8,9,10]. Dynamical consequences of predator interference in a tri-trophic model food chain is investigated by R K Naji et al[11]. Three-species food-chain model with Beddington DeAngelis type functional response has been studied by Wang and Zhao[12].Meng Fan et al.[9] investigated the dynamical interaction among prey (bird), mesopredator (rat), and superpredator (cat) and developed a prey-mesopredator-superpredator (i.e. bird-rat-cat) BRC model, where the predator’s functional response is derived based on classical Holling’s time budget arguments. They have explored possible control strategies to save or restore the bird by controlling or eliminating the rat or the cat when the bird is endangered. They do not show under what conditions all the three species (BRC) will coexist and global stability analysis of interior equilibrium point is also not carried out. In view of the above, the main purpose of this paper is to construct a general model to study the effect of exotic predator on a system consisting of a native prey population and a native predator population by considering Holling type two functional response with exotic predator interference for native predator population and Beddington type functional response for exotic predator population.
2. Basic Assumptions and Mathematical Model
- Let
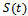 denotes the density of native prey population,
denotes the density of native prey population, 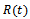 denotes the density of native predator population and
denotes the density of native predator population and 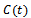 denotes the density of exotic predator population. We assume that r and k are growth rate and carrying capacity of native prey population respectively.
denotes the density of exotic predator population. We assume that r and k are growth rate and carrying capacity of native prey population respectively. 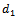 and
and 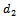 are death rate of native predator population and exotic predator population respectively. b is the interference due to exotic predator population.
are death rate of native predator population and exotic predator population respectively. b is the interference due to exotic predator population. 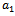 is the predation rate of native prey population by native predator population.
is the predation rate of native prey population by native predator population. 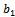 is the growth rate of native predator population due to predation of native prey population.
is the growth rate of native predator population due to predation of native prey population. 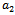 is the predation rate of native predator population by exotic predator population.
is the predation rate of native predator population by exotic predator population. 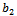 is the growth rate of exotic predator population due to predation of native predator population. h is the half saturation constant of native prey population. w is the wasting time to searching native predator by exotic predator.
is the growth rate of exotic predator population due to predation of native predator population. h is the half saturation constant of native prey population. w is the wasting time to searching native predator by exotic predator. 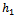 is the handling time to handle native predator by exotic predator. In view of above, the resultant system dynamics is governed by the following system of differential equations:Model 1 (With exotic species)
is the handling time to handle native predator by exotic predator. In view of above, the resultant system dynamics is governed by the following system of differential equations:Model 1 (With exotic species)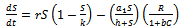 | (1) |
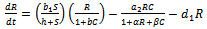 | (2) |
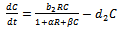 | (3) |
 and
and 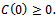 where
where 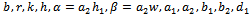 and
and 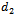 are positive constants.In the absence of exotic predator species the above system (1) – (3) is governed by the following system of differential equations:Model 2 ( Without exotic species)
are positive constants.In the absence of exotic predator species the above system (1) – (3) is governed by the following system of differential equations:Model 2 ( Without exotic species)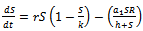 | (4) |
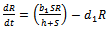 | (5) |
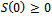 and
and 
3. Equillibria of the System
- In this section, we analyze the system of equation (4) – (5) under the initial conditions. We find all the possible equillibria of the system of equation (4) – (5). The system has three feasible equillibria, namely(i) Trivial equilibrium point
 (ii) Axial equilibrium point
(ii) Axial equilibrium point 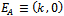 (iii) Positive interior equilibrium point
(iii) Positive interior equilibrium point 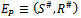 Where
Where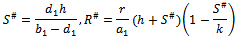 The positive equilibrium point
The positive equilibrium point 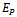 exist if
exist if 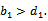 We now analyze the system of equation (1) – (3) under the initial conditions. The system has four feasible equilibria, namely(i)Trivial equilibrium point
We now analyze the system of equation (1) – (3) under the initial conditions. The system has four feasible equilibria, namely(i)Trivial equilibrium point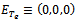 (ii)Axial equilibrium point
(ii)Axial equilibrium point 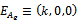 (iii)Boundary equilibrium point
(iii)Boundary equilibrium point 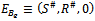 where
where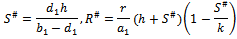 The boundary equilibrium point
The boundary equilibrium point 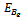 exist if
exist if 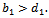 (iv)Positive interior equilibrium point
(iv)Positive interior equilibrium point 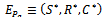 where
where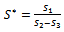 | (6) |
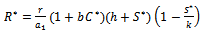 | (7) |
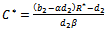 | (8) |
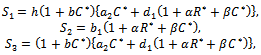 The Positive interior equilibrium point
The Positive interior equilibrium point 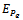 exist if
exist if 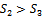 and
and 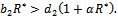 Now, we will study the existence of positive interior equilibrium point
Now, we will study the existence of positive interior equilibrium point 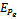 Put value of
Put value of 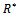 from equation (7) in equation (6) we get,
from equation (7) in equation (6) we get,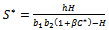 | (9) |
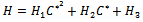
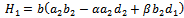
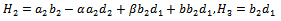 Putting value of
Putting value of 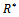 from equation (7) and putting value of
from equation (7) and putting value of 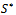 from equation (9) in equation (8) we get
from equation (9) in equation (8) we get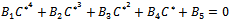 where
where 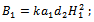
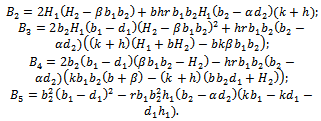 Therefore unique positive root
Therefore unique positive root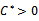 if
if 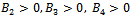 and
and 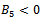
4. Dynamic Behaviour of the System
- The following results may be noted regarding the local stability of the equilibria of the model 2 given by (4)-(5).(1). Equilibrium point
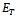 of the model is unstable in the absence of exotic species.(2). Equilibrium point
of the model is unstable in the absence of exotic species.(2). Equilibrium point 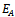 of the model is stable when there is no exotic species present in the system if
of the model is stable when there is no exotic species present in the system if 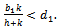 (3). Interior equilibrium point
(3). Interior equilibrium point 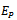 of the model is locally asymptotically stable when there is no exotic species present in the system if
of the model is locally asymptotically stable when there is no exotic species present in the system if 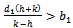 is satisfied.The following results may be noted regarding the local stability of the equilibria of the model 1 given by (1)-(4). (1). Equilibrium point
is satisfied.The following results may be noted regarding the local stability of the equilibria of the model 1 given by (1)-(4). (1). Equilibrium point 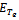 of the model is unstable in the presence of exotic species.(2). Equilibrium point
of the model is unstable in the presence of exotic species.(2). Equilibrium point 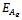 of the model is stable when exotic species is present in the system if
of the model is stable when exotic species is present in the system if 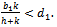 (3). Equilibrium point
(3). Equilibrium point 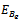 of the model is stable when exotic species is present in the system if
of the model is stable when exotic species is present in the system if 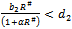 and
and  are satisfied.(4). For the sake of simplicity, the equilibrium points
are satisfied.(4). For the sake of simplicity, the equilibrium points 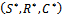 of the system (1)-(3) is shifted to new points
of the system (1)-(3) is shifted to new points 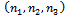 through transformations
through transformations 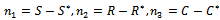 In term of the new variables, the dynamical system (1)-(3) can be written as in matrix form as
In term of the new variables, the dynamical system (1)-(3) can be written as in matrix form as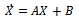 | (10) |
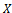 denotes the derivative with respect to time. Here
denotes the derivative with respect to time. Here 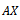 is the linear part of the system and
is the linear part of the system and 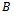 represents the nonlinear part. Moreover,
represents the nonlinear part. Moreover, 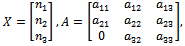 | (11) |
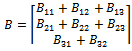 | (12) |
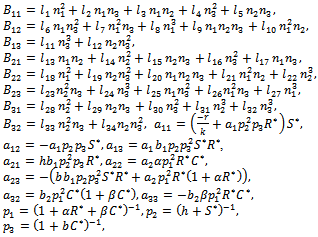
 The eigen values of the matrix
The eigen values of the matrix 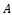 help to understand the stability of the system. The characteristic equation for the variational matrix
help to understand the stability of the system. The characteristic equation for the variational matrix 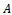 is given by
is given by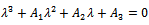 | (13) |
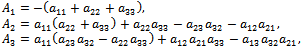 Using the Routh-Hurwitz criteria, we derive that the equilibrium point
Using the Routh-Hurwitz criteria, we derive that the equilibrium point  is locally asymptotically stable, if
is locally asymptotically stable, if 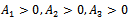 and
and 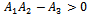 are being satisfied.Now, we are in a position to make an attempt to find out the condition under which the system undergoes Hopf-bifurcation[13]. For this purpose, we choose the parameter ‘
are being satisfied.Now, we are in a position to make an attempt to find out the condition under which the system undergoes Hopf-bifurcation[13]. For this purpose, we choose the parameter ‘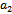 ’ as bifurcation parameter as it plays a crucial role to describe predation rate of native predator population by exotic predator population. We shall now apply the Liu’s criteria[14] to obtain the conditions for small amplitude periodic solution arising from Hopf-bifurcation. As the equilibrium population densities are function of ‘
’ as bifurcation parameter as it plays a crucial role to describe predation rate of native predator population by exotic predator population. We shall now apply the Liu’s criteria[14] to obtain the conditions for small amplitude periodic solution arising from Hopf-bifurcation. As the equilibrium population densities are function of ‘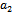 ’, the coefficient of the characteristic equation (13) is a function of parameter ‘
’, the coefficient of the characteristic equation (13) is a function of parameter ‘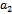 ’ and hence we can use the notation
’ and hence we can use the notation 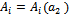 for
for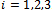 . Now noting that the quantities
. Now noting that the quantities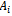 ’s are smooth function of parameter, ‘
’s are smooth function of parameter, ‘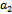 ’we first state for our case, the definition of a simple Hopf-bifurcation.If a crucial value
’we first state for our case, the definition of a simple Hopf-bifurcation.If a crucial value 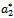 of parameter ‘
of parameter ‘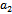 ’ is found such that (i) a simple pair of complex conjugate eigenvalues of characteristic equation (13) exist, say,
’ is found such that (i) a simple pair of complex conjugate eigenvalues of characteristic equation (13) exist, say, 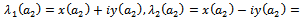
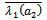 such that they becomes purely imaginary at
such that they becomes purely imaginary at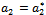 , i.e.
, i.e. 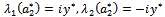 with
with 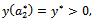 whereas the other eigen value remain real and negative; and the transversality condition (ii)
whereas the other eigen value remain real and negative; and the transversality condition (ii) 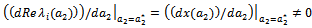 is satisfied, then at
is satisfied, then at  , we have a simple Hopf-bifurcation. Without knowing eigen value[14] proved that (referring the result to the current case): if
, we have a simple Hopf-bifurcation. Without knowing eigen value[14] proved that (referring the result to the current case): if 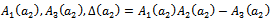 are smooth function of the parameter ‘
are smooth function of the parameter ‘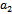 ’ in an open interval containing
’ in an open interval containing 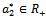 such that the following condition hold.
such that the following condition hold.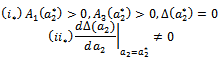 Then
Then 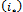 and
and 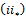 are equivalent to conditions
are equivalent to conditions 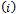 and
and 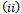 for the occurrence of a simple Hopf-bifurcation at
for the occurrence of a simple Hopf-bifurcation at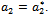 Hence we can propose the following theorem:Theorem 4.1 If a critical value
Hence we can propose the following theorem:Theorem 4.1 If a critical value 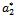 of parameter ‘
of parameter ‘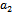 ’ is found such that
’ is found such that 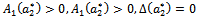 and further
and further 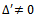 (where prime denotes differentiation with respect to
(where prime denotes differentiation with respect to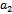 ) then system (1)-(3) undergoes Hopf-bifurcation around
) then system (1)-(3) undergoes Hopf-bifurcation around 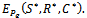 Next, we seek a transformation matrix
Next, we seek a transformation matrix 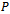 which reduces the matrix
which reduces the matrix 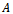 to the form
to the form 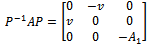 | (14) |
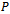 is given as
is given as | (15) |
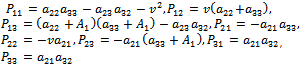 To achieve the normal form of (10), we make another change of variable, that is,
To achieve the normal form of (10), we make another change of variable, that is, 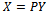 , where
, where 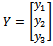 Through some algebraic manipulation, (10) takes the form
Through some algebraic manipulation, (10) takes the form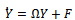 | (16) |
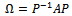 and
and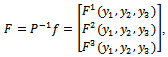 f is given by
f is given by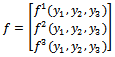 | (17) |
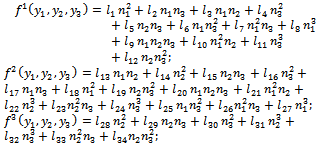 where,
where,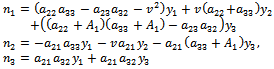 Equation (16) is the normal form of (10) from which the stability coefficient can be computed. In (10), on the right hand side the first term is linear and second one is nonlinear in
Equation (16) is the normal form of (10) from which the stability coefficient can be computed. In (10), on the right hand side the first term is linear and second one is nonlinear in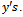 For evaluating the direction of bifurcating solution, we can evaluate the following quantities at
For evaluating the direction of bifurcating solution, we can evaluate the following quantities at 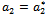 and origin
and origin 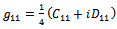 | (18) |
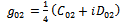 | (19) |
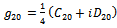 | (20) |
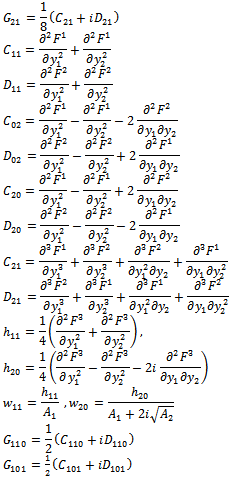 | (21) |
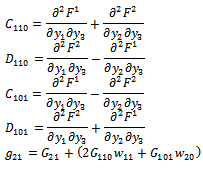 | (22) |
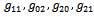 from (18),(19),(20), and (22), respectively. Thus, we can compute the following values:
from (18),(19),(20), and (22), respectively. Thus, we can compute the following values: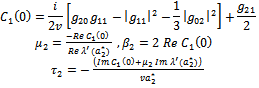 | (23) |
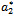 .Theorem 4.2: The parameter
.Theorem 4.2: The parameter  determine the direction of the Hopf-bifurcation[15] if
determine the direction of the Hopf-bifurcation[15] if 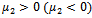 , then the Hopf-bifurcation is supercritical (subcritical) and the bifurcation periodic solutions exist for
, then the Hopf-bifurcation is supercritical (subcritical) and the bifurcation periodic solutions exist for 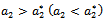 ;
; 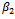 determine the stability of bifurcating periodic solution, the bifurcation periodic solutions are orbitally asymptotically stable (unstable) if
determine the stability of bifurcating periodic solution, the bifurcation periodic solutions are orbitally asymptotically stable (unstable) if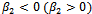 ;
; 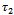 determine the period of the bifurcating periodic solution; the period increase (decrease) if
determine the period of the bifurcating periodic solution; the period increase (decrease) if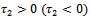 .
.5. Boundedness of the System
- Lemma 5.1 All the solutions of system (4)-(5) with the positive initial condition are uniformly bounded within the region
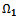 where
where 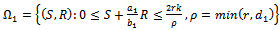 is a region of attraction.Proof. Proof is obvious.Lemma 5.2 All the solutions of system (1)-(3) with the positive initial condition are uniformly bounded within the region
is a region of attraction.Proof. Proof is obvious.Lemma 5.2 All the solutions of system (1)-(3) with the positive initial condition are uniformly bounded within the region 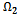 where
where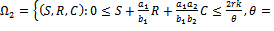
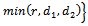 is a region of attraction.Proof. We assume that the right hand sides of the system (1)-(3) are smooth function of
is a region of attraction.Proof. We assume that the right hand sides of the system (1)-(3) are smooth function of 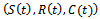 of
of 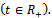 Let
Let 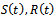 and
and 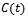 be any solution with positive initial condition
be any solution with positive initial condition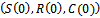 . From equation (1), we obtain
. From equation (1), we obtain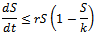 then by usual comparison theorem[16]
then by usual comparison theorem[16] 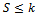 We consider a time dependent function
We consider a time dependent function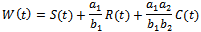 The time derivative of
The time derivative of 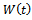 along the solution of the system (1)-(3) is
along the solution of the system (1)-(3) is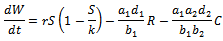 Since
Since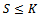 , the above expression reduces to
, the above expression reduces to 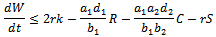 Taking
Taking 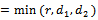 , we get
, we get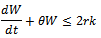 Applying comparison theorem[17] we obtain
Applying comparison theorem[17] we obtain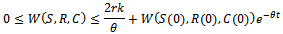 and for
and for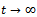 ,
,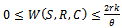 Therefore all the solutions of system (1)-(3) initiated at
Therefore all the solutions of system (1)-(3) initiated at 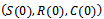 enter into the region
enter into the region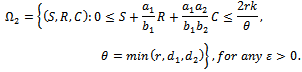 Thus all the solutions of system (1)-(3) are uniformly bounded at
Thus all the solutions of system (1)-(3) are uniformly bounded at 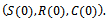 This completes the proof of the lemma.
This completes the proof of the lemma.6. Global Stability Analysis of the Interior Equilibrium Point
- Theorem 6.1: The positive interior equilibrium point
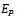 of the model 2 is globally asymptotically stable in absence of exotic predator species if
of the model 2 is globally asymptotically stable in absence of exotic predator species if 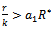 is satisfied.Proof: Proof is obvious.Theorem 6.2: If the following inequalities hold
is satisfied.Proof: Proof is obvious.Theorem 6.2: If the following inequalities hold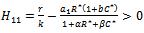 | (24) |
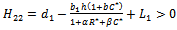 | (25) |
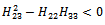 | (26) |
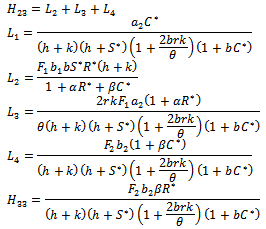
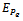 is globally asymptotically stable with respect to solutions initiating in the interior of the positive orthant. Proof: Consider the following positive definite function
is globally asymptotically stable with respect to solutions initiating in the interior of the positive orthant. Proof: Consider the following positive definite function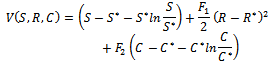 where
where 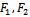 are positive constants to be chosen appropriately.Differentiating
are positive constants to be chosen appropriately.Differentiating  with respect to t, we get
with respect to t, we get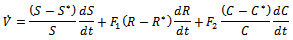 Substituting values of
Substituting values of 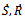 and
and 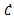 from the system of equations (1)-(3) in the above equation and after doing some algebraic manipulation, we get
from the system of equations (1)-(3) in the above equation and after doing some algebraic manipulation, we get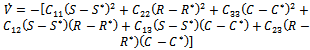 where
where 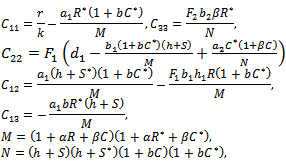 Then a sufficient conditions[18] for
Then a sufficient conditions[18] for 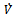 to be negative definite is that
to be negative definite is that 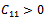 | (27) |
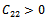 | (28) |
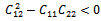 | (29) |
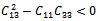 | (30) |
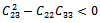 | (31) |
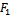 and
and 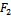 such a way
such a way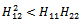 | (32) |
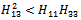 | (33) |
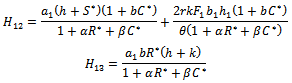 conditions (32) and (33) hold. However (32) implies (29) and (33) implies (30). Then above sufficient conditions reduce into the following inequalities.
conditions (32) and (33) hold. However (32) implies (29) and (33) implies (30). Then above sufficient conditions reduce into the following inequalities. | (34) |
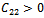 | (35) |
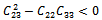 | (36) |
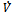 is negative definite and so
is negative definite and so 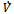 is a Liapunov function with respect to
is a Liapunov function with respect to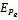 , proving the theorem.
, proving the theorem. 7. Simulation Analysis
- We have gained analytical understanding of possible dynamics of the native prey-predator, exotic predator model. We now perform some simulation work for the model 2 with set of parameters.
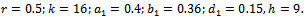 For this choice of parameters we get a unique co-existing equilibrium point
For this choice of parameters we get a unique co-existing equilibrium point 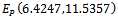 of Model 2 along with
of Model 2 along with 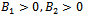 and hence
and hence 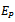 is locally asymptotically stable (see Figure 1(a), 1(b)). We now perform simulation work for the model 1 with set of parameters.
is locally asymptotically stable (see Figure 1(a), 1(b)). We now perform simulation work for the model 1 with set of parameters.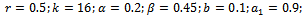
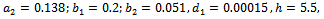
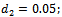 For this choice of parameters we get a unique co-existing equilibrium
For this choice of parameters we get a unique co-existing equilibrium 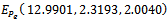 of Model 1 along with
of Model 1 along with 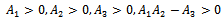 and hence
and hence 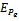 is locally asymptotically stable (see Figure 4(a), 4(b)). Now, we discuss the dynamical behaviour of the model 1 by varying the parameter
is locally asymptotically stable (see Figure 4(a), 4(b)). Now, we discuss the dynamical behaviour of the model 1 by varying the parameter 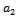 taking the above set of parametric values. For this, we find out the positive roots of the equation
taking the above set of parametric values. For this, we find out the positive roots of the equation 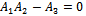 and we obtain three positive roots of this equation i.e.
and we obtain three positive roots of this equation i.e. 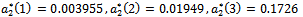 (See Figure 7(a), 7(b), 7(c)). At
(See Figure 7(a), 7(b), 7(c)). At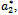 one pair of eigen values of the characteristic equation (13) are of the form
one pair of eigen values of the characteristic equation (13) are of the form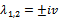 , where
, where 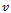 is a positive real number and hence the system (1)-(3) undergoes a Hopf-bifurcation at
is a positive real number and hence the system (1)-(3) undergoes a Hopf-bifurcation at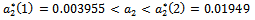 . For
. For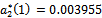 we get
we get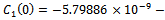
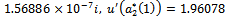 . From these values, it follows from (23) that
. From these values, it follows from (23) that 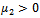 and
and 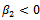 showing that the bifurcation takes place when
showing that the bifurcation takes place when 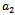 crosses
crosses 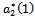 to the right
to the right 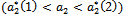 and the corresponding periodic orbits are orbitally asymptotically stable (See Figure 5(a) and 5(b) for
and the corresponding periodic orbits are orbitally asymptotically stable (See Figure 5(a) and 5(b) for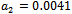 ). For
). For 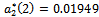 we get
we get 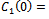
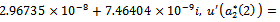
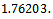 From these values, it follows from (23) that
From these values, it follows from (23) that 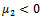 and
and 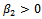 showing that the bifurcation takes when
showing that the bifurcation takes when 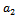 crosses
crosses 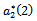 to the left
to the left 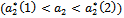 and the corresponding periodic orbits are orbitally asymptotically unstable. The system (1)-(3) undergoes a Hopf-bifurcation at
and the corresponding periodic orbits are orbitally asymptotically unstable. The system (1)-(3) undergoes a Hopf-bifurcation at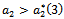 . For
. For 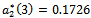 we get
we get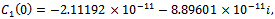
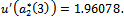 From these values, it follow from (23) that
From these values, it follow from (23) that 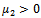 and
and 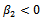 showing that the bifurcation takes when
showing that the bifurcation takes when 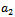 crosses
crosses 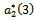 to the right
to the right 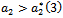 , and the corresponding periodic orbits are orbitally asymptotically stable (See Figure 6(a) and 6(b)
, and the corresponding periodic orbits are orbitally asymptotically stable (See Figure 6(a) and 6(b) 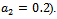
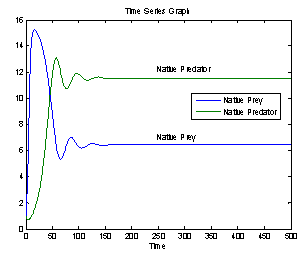 | Figure 1(a). Stable population distribution for native prey and native predator species |
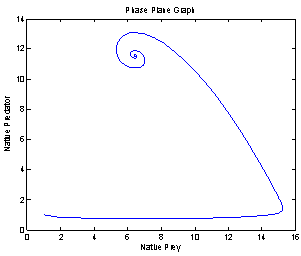 | Figure 1(b). Phase space graph between native prey and native predator species |
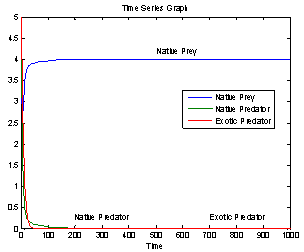 | Figure 2. Time series graph for native prey , native predator and exotic predator species |
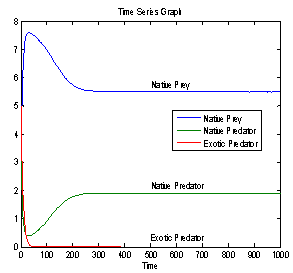 | Figure 3. Time series graph for native prey , native predator and exotic predator species |
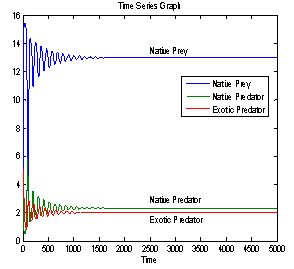 | Figure 4(a). Stable population distribution for native prey , native predator and exotic predator species |
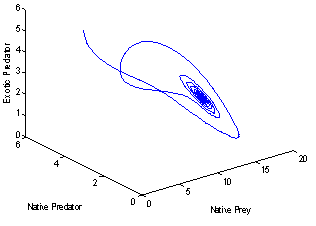 | Figure 4(b). Phase space graph for native prey , native predator and exotic predator species |
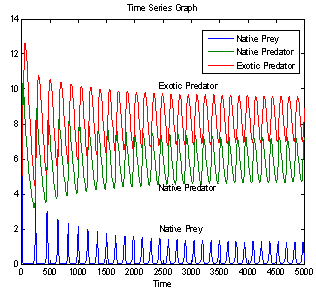 | Figure 5(a). Time series graph for native prey , native predator and exotic predator species at  |
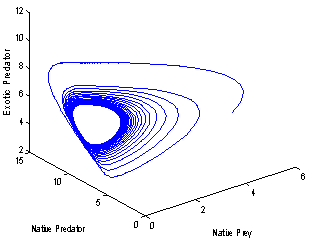 | Figure 5(b). Phase space graph for native prey , native predator and exotic predator species at  |
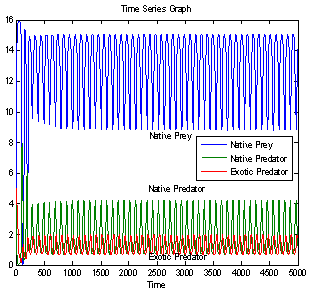 | Figure 6(a). Time series graph for native prey , native predator and exotic predator species at 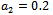 |
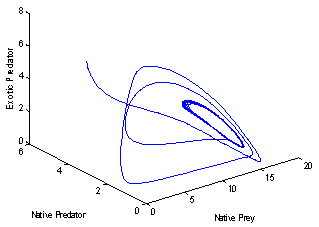 | Figure 6(b). Phase space graph for native prey , native predator and exotic predator species at 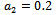 |
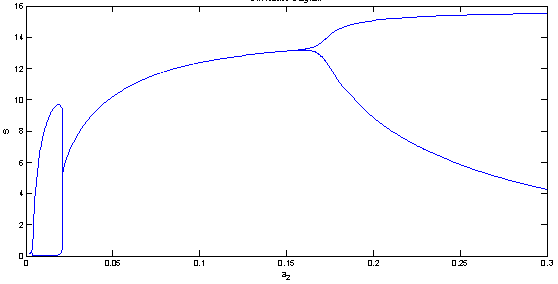 | Figure 8(a). Bifurcation diagram of the native prey species with respect to predation rate  |
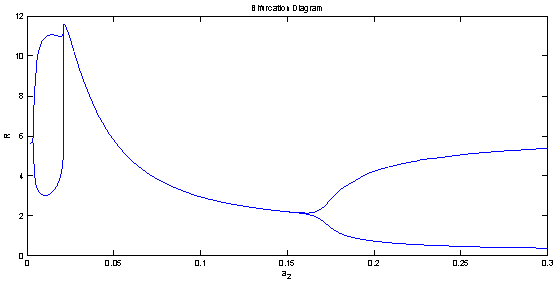 | Figure 8(b). Bifurcation diagram of the native predator species with respect to predation rate  |
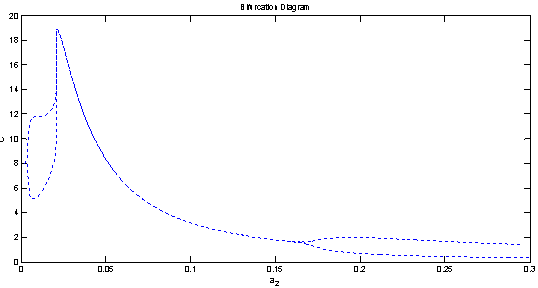 | Figure 8(c). Bifurcation diagram of the exotic predator species with respect to predation rate 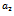 |
8. Conclusions
- In this paper, a mathematical model is proposed to study the effect of exotic predator population on a native prey-predator species system. The local stability analyses of all the feasible equilibria are carried out. We observed that if the axial equilibrium point
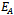 of model 2 is stable then interior equilibrium point
of model 2 is stable then interior equilibrium point 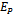 does not exist and if interior equilibrium point
does not exist and if interior equilibrium point 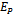 of model 2 exists then axial equilibrium point
of model 2 exists then axial equilibrium point 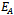 is unstable. From the stability of axial equilibrium point EAe [see figure 2], it may be concluded that native prey population will survive and native and exotic population may go to extinction. From the stability of boundary equilibrium point EBe [see figure 3], it is observed that the exotic predator population will not survive and consequently native prey-predator population will coexist. The global stability analysis of both the models 1 and 2 are carried out, and the possibility of Hopf- bifurcation of the interior equilibrium point is investigated. We observed that the positive interior equilibrium point
is unstable. From the stability of axial equilibrium point EAe [see figure 2], it may be concluded that native prey population will survive and native and exotic population may go to extinction. From the stability of boundary equilibrium point EBe [see figure 3], it is observed that the exotic predator population will not survive and consequently native prey-predator population will coexist. The global stability analysis of both the models 1 and 2 are carried out, and the possibility of Hopf- bifurcation of the interior equilibrium point is investigated. We observed that the positive interior equilibrium point 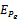 is stable for
is stable for 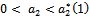 and
and 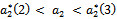 (see figure 8(a), 8(b), 8(c)). The switching in stability behaviour based on predation rate of exotic predator;
(see figure 8(a), 8(b), 8(c)). The switching in stability behaviour based on predation rate of exotic predator; 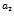 is also observed (see figure 8(a), 8(b), 8(c)). We also determine the stability and direction of periodic bifurcation from the positive equilibrium at the critical point. Finally we conclude that invasion of exotic predator is harmful to native prey-predator system. We also clear that exotic predator is harmful to native predator and helpful to native prey. The predation rate of exotic predator creates complex phenomena in the system. The present work may be extended by considering the migration of the population.
is also observed (see figure 8(a), 8(b), 8(c)). We also determine the stability and direction of periodic bifurcation from the positive equilibrium at the critical point. Finally we conclude that invasion of exotic predator is harmful to native prey-predator system. We also clear that exotic predator is harmful to native predator and helpful to native prey. The predation rate of exotic predator creates complex phenomena in the system. The present work may be extended by considering the migration of the population.  Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML