-
Paper Information
- Next Paper
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Computational and Applied Mathematics
p-ISSN: 2165-8935 e-ISSN: 2165-8943
2012; 2(6): 276-289
doi: 10.5923/j.ajcam.20120206.06
Modelling Effect of Toxic Metal on the Individual Plant Growth: A Two Compartment Model
O. P. Misra, Preety Kalra
School of Mathematics and Allied Sciences, Jiwaji University, Gwalior, 474011, M.P., India
Correspondence to: Preety Kalra, School of Mathematics and Allied Sciences, Jiwaji University, Gwalior, 474011, M.P., India.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
A two compartment mathematical model for the individual plant growth under the stress of toxic metal is studied. In the model it is assumed that the uptake of toxic metal adsorbed on the surface of soil by the plant is through root compartment thereby decreasing the root dry weight and shoot dry weight due to decrease in nutrient concentration in each compartment. In order to visualize the effect of toxic metal on plant growth, we have studied two models that is, model for plant growth with no toxic effect and model for plant growth with toxic effect. From the analysis of the models the criteria for plant growth with and without toxic effects are derived. The numerical simulation is done using Matlab to support the analytical results.
Keywords: Nutrient Concentration, Dry weight, Toxic metal, Model, Equilibria, Stability
Cite this paper: O. P. Misra, Preety Kalra, "Modelling Effect of Toxic Metal on the Individual Plant Growth: A Two Compartment Model", American Journal of Computational and Applied Mathematics, Vol. 2 No. 6, 2012, pp. 276-289. doi: 10.5923/j.ajcam.20120206.06.
Article Outline
1. Introduction
- Soil normally contains a low concentration of heavy metals such as copper (Cu) and zinc (Zn), which are the essential macronutrients for the optimum growth of the plants. Metals such as cadmium (Cd), arsenic (Ar), chromium (Cr), lead (Pb), nickel(Ni), mercury(Hg) and selenium (Se) toxic to plants are not usually found in agricultural soil[1]. Over the last few years, the level of heavy metals are increasing in the agricultural fields as a consequence of increasing environmental pollution from industrial, agricultural, energy and municipal wastes. A reduction in plant growth has been observed due to the presence of elevated levels of heavy metals like cadmium, arsenic, nickel, lead and mercury[2]. Cadmium (Cd) is among the most widespread heavy metals found in the surface soil layer which inhibits the uptake of nutrients by plants and as well as its growth[3]. The inhibition of plant growth can be caused by the phytotoxic effect of cadmium on different processes in plants, including respiration, photosynthesis, carbohydrate metabolism and water relation[4]. Cadmium (Cd) ia a toxic metal, causing phytotoxicity, and its uptake and accumulation in plants causes reduction in photosynthesis, diminishes water and nutrient uptake[5]. Heavy metals interfere with the uptake and distribution of essential mineral nutrients in a plant, causing deficiencies and nutrient imbalance[6]. The toxic metals in the soil system could result in the leaching of essential cation away from the rooted zone, decreasing plant nutrient uptake causing root damage[7]. Cadmium inhibits root and shoot growth and yield production, affects nutrient uptake and homeostasis. Cadmium is a highly toxic, metallic soil contaminant, which adversely affects the plant growth especially at early stage reducing the crop production[8]. The reduction of dry weight by
 toxicity could be the direct consequence of the inhibition of chlorophyll synthesis and photosynthesis[9]. Excessive amount of
toxicity could be the direct consequence of the inhibition of chlorophyll synthesis and photosynthesis[9]. Excessive amount of  may also cause decrease in uptake of nutrient elements, inhibition of various enzyme activities, induction of oxidative stress including alterations in the enzymes of the antioxidant defense system[10]. Aluminium (Al) interferes with the uptake, transport and utilization of essential nutrients including
may also cause decrease in uptake of nutrient elements, inhibition of various enzyme activities, induction of oxidative stress including alterations in the enzymes of the antioxidant defense system[10]. Aluminium (Al) interferes with the uptake, transport and utilization of essential nutrients including  ,
, 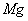 ,
, 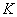 ,
, 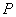 ,
, 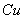 ,
, 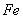 ,
, 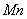 and
and 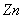 in plant system[11]. Metals inhibit the activities of several enzymes, seed germination and seedling growth[12-15]. Seed gemination inhibition by heavy metals has been reported by many researchers[16-18]. Agricultural research almost completely rely upon experimental and empirical works, combined with statistical analysis and very few mathematical modelling analysis has been carried out in this direction[3-4],[19-20]. Many of the models that are currently used by agronomists and foresters to predict harvests and schedule fertilization, irrigation and pesticides application are of empirical form. A major limitation in all these approaches is the unpredictability of the environmental inputs[21]. Thornley initiated the work related to the mathematical modelling of individual plant growth processes and mathematical models were applied to a wide variety of topics in plant physiology[22]. The majority of these focuses on processes that are modelled independently such as photosynthesis, fluid transport, respiration, transpiration and stomatal response and the general goal of the models was to predict the effect of a variety of environmental factors, including radiation input, humidity, wind, CO2 concentration and temperature on these process rates. The soil-nutrient-plant interaction represents a good example of a relationship that operates at individual, population, and ecosystem levels. Nutrients influence individual plant growth, which has subsequent effect on population growth dynamics which in turn influence production of standing crop. The models that have been developed to describe the growth of individual plants in crop has been classified by Benamin and Hardwick[23], according to the assumption that how resources are shared. A continuous-time model for the growth and reproduction of a perennial herb with discrete growing season is considered in[24] and optimal resource allocation in perennial plants has been determined and studied. In the paper[25], a transient three-dimensional model for soil water and solute transport with simultaneous root growth, root water and nutrient uptake is studied and discussed. In this paper, authors have presented a model to study the interactive relationships between changing soil-water and nutrient status and root activity. The authors in the paper[19] have studied the influence of acid deposition on forests by means of a mathematical model taking the state variables as forest dry weight, aluminium concentration in trees and soil, and proton concentration in soil. Referrence[3] have given a mathematical model to study the effect of cadmium (Cd) on nutrient uptake by crop such as Barley and have shown through their model that how the accumulation of Cd in plants inhibit its growth rate. Experimental and mathematical simulation to study the effects of toxic metal; cadmium on the plant growth promoting rhizobacteria and plant interaction have been carried out by[4]. Nitrogen dynamics in soil, its availability to the crop and the effects of nitrogen deficiency on crop performance were studied in the model given by the researchers[26]. A non-spatial, size- structured continuum model of plant growth, without focusing on a particular species, but with emphasis on a dense tree-dominated forest is considered and studied by[27] and in this paper a closed form solution for the equilibrium size density distribution is obtained along with the analytical conditions for communities persistence. Crops and vegetables grown on polluted soil accumulate heavy metals that cause decrease in their yield, and in order to study the uptake of heavy metals and its accumulation by crops, mathematical models can be used. In paper[20], a study has been conducted through mathematical model to understand the cadmium uptake by radish, carrot, spinach and cabbage. In this paper a dynamic macroscopic numerical model for heavy metal transport and its uptake by vegetables in the root zone is considered and analysed numerically. A very few mathematical models to study the effects of toxic metal on plant growth exist[3-4],[19-20].In view of the above, therefore in this paper, a two compartment mathematical model for the plant growth under the stress of toxic metal is proposed and analyzed. For the modelling purpose, the plant is divided into root and shoot compartments in which the state variables considered are nutrient concentration and dry weight. In the model it is assumed that the uptake of toxic metal adsorbed on the surface of soil by the plant is through root compartment thereby decreasing the root dry weight and shoot dry weight due to decrease in nutrient concentration in each compartment. In the model it is further assumed that the maximum root dry weight and shoot dry weight decrease due to the presence of toxic metal in root compartment. From the analytical and numerical analysis of the model the criteria for plant growth under the stress of toxic metal are derived.
in plant system[11]. Metals inhibit the activities of several enzymes, seed germination and seedling growth[12-15]. Seed gemination inhibition by heavy metals has been reported by many researchers[16-18]. Agricultural research almost completely rely upon experimental and empirical works, combined with statistical analysis and very few mathematical modelling analysis has been carried out in this direction[3-4],[19-20]. Many of the models that are currently used by agronomists and foresters to predict harvests and schedule fertilization, irrigation and pesticides application are of empirical form. A major limitation in all these approaches is the unpredictability of the environmental inputs[21]. Thornley initiated the work related to the mathematical modelling of individual plant growth processes and mathematical models were applied to a wide variety of topics in plant physiology[22]. The majority of these focuses on processes that are modelled independently such as photosynthesis, fluid transport, respiration, transpiration and stomatal response and the general goal of the models was to predict the effect of a variety of environmental factors, including radiation input, humidity, wind, CO2 concentration and temperature on these process rates. The soil-nutrient-plant interaction represents a good example of a relationship that operates at individual, population, and ecosystem levels. Nutrients influence individual plant growth, which has subsequent effect on population growth dynamics which in turn influence production of standing crop. The models that have been developed to describe the growth of individual plants in crop has been classified by Benamin and Hardwick[23], according to the assumption that how resources are shared. A continuous-time model for the growth and reproduction of a perennial herb with discrete growing season is considered in[24] and optimal resource allocation in perennial plants has been determined and studied. In the paper[25], a transient three-dimensional model for soil water and solute transport with simultaneous root growth, root water and nutrient uptake is studied and discussed. In this paper, authors have presented a model to study the interactive relationships between changing soil-water and nutrient status and root activity. The authors in the paper[19] have studied the influence of acid deposition on forests by means of a mathematical model taking the state variables as forest dry weight, aluminium concentration in trees and soil, and proton concentration in soil. Referrence[3] have given a mathematical model to study the effect of cadmium (Cd) on nutrient uptake by crop such as Barley and have shown through their model that how the accumulation of Cd in plants inhibit its growth rate. Experimental and mathematical simulation to study the effects of toxic metal; cadmium on the plant growth promoting rhizobacteria and plant interaction have been carried out by[4]. Nitrogen dynamics in soil, its availability to the crop and the effects of nitrogen deficiency on crop performance were studied in the model given by the researchers[26]. A non-spatial, size- structured continuum model of plant growth, without focusing on a particular species, but with emphasis on a dense tree-dominated forest is considered and studied by[27] and in this paper a closed form solution for the equilibrium size density distribution is obtained along with the analytical conditions for communities persistence. Crops and vegetables grown on polluted soil accumulate heavy metals that cause decrease in their yield, and in order to study the uptake of heavy metals and its accumulation by crops, mathematical models can be used. In paper[20], a study has been conducted through mathematical model to understand the cadmium uptake by radish, carrot, spinach and cabbage. In this paper a dynamic macroscopic numerical model for heavy metal transport and its uptake by vegetables in the root zone is considered and analysed numerically. A very few mathematical models to study the effects of toxic metal on plant growth exist[3-4],[19-20].In view of the above, therefore in this paper, a two compartment mathematical model for the plant growth under the stress of toxic metal is proposed and analyzed. For the modelling purpose, the plant is divided into root and shoot compartments in which the state variables considered are nutrient concentration and dry weight. In the model it is assumed that the uptake of toxic metal adsorbed on the surface of soil by the plant is through root compartment thereby decreasing the root dry weight and shoot dry weight due to decrease in nutrient concentration in each compartment. In the model it is further assumed that the maximum root dry weight and shoot dry weight decrease due to the presence of toxic metal in root compartment. From the analytical and numerical analysis of the model the criteria for plant growth under the stress of toxic metal are derived. 2. Mathematical Model
- Model 1 (Model with no toxic effect):In this model the plant growth dynamics is studied by assuming that the plant is divided into root and shoot (stem, leaf, flower) compartments in which the state variables associated with the each compartment are nutrient concentration and dry weight. Let
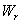 and
and 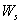 denote the root dry weight and shoot dry weight respectively.
denote the root dry weight and shoot dry weight respectively. 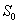 and
and 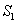 denote the nutrient concentration in root and shoot respectively. With these notations, the mathematical model of the plant growth dynamics is given by the following system of nonlinear differential equations:
denote the nutrient concentration in root and shoot respectively. With these notations, the mathematical model of the plant growth dynamics is given by the following system of nonlinear differential equations: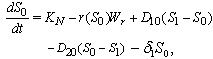 | (1) |
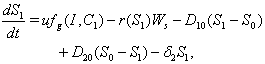 | (2) |
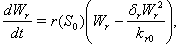 | (3) |
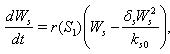 | (4) |
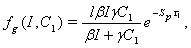 | (5) |
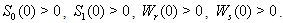 In the present analysis we assume the following forms for growth functions
In the present analysis we assume the following forms for growth functions 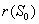 and
and 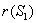 [22],[28] :
[22],[28] : 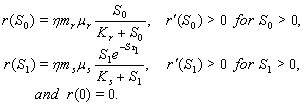 | (6) |
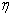 is the utilization coefficient.
is the utilization coefficient. 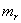 and
and 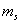 are the proportion of total dry weight allocated to root and shoot dry weight respectively.
are the proportion of total dry weight allocated to root and shoot dry weight respectively. 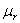 and
and 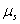 are the resource-saturated rates of resource uptake per unit of root and shoot dry weight respectively.
are the resource-saturated rates of resource uptake per unit of root and shoot dry weight respectively. 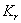 and
and 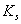 are half saturation constants.
are half saturation constants. 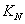 is the rate of supply of nutrient.
is the rate of supply of nutrient. 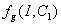 is the specific gross photosynthetic rate[22].
is the specific gross photosynthetic rate[22]. 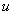 is the fraction of shoot in the form of leaf tissue.
is the fraction of shoot in the form of leaf tissue. 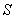 is senescence constant.
is senescence constant. 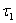 is the maximum age of shoot of plant.
is the maximum age of shoot of plant. 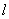 is the specific leaf area of whole plant.
is the specific leaf area of whole plant. 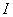 is the light flux density incident on the leaves in shoot compartment.
is the light flux density incident on the leaves in shoot compartment. 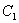 is the
is the 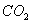 density in plant.
density in plant. 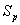 is the rate of senescence of the photosynthesis. β is the photochemical efficency. γ is the conductance to
is the rate of senescence of the photosynthesis. β is the photochemical efficency. γ is the conductance to 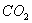 .
.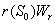 and
and 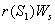 represent the use of nutrient by root and shoot respectively[26]. In plant growth, it is considered that during the initial stage, i.e., during the lag phase, the rate of plant growth is slow. Rate of growth then increases rapidly during the exponential phase. After some time the growth rate slowly decreases due to limitation of nutrient. This phase constitutes the stationary phase . The terms
represent the use of nutrient by root and shoot respectively[26]. In plant growth, it is considered that during the initial stage, i.e., during the lag phase, the rate of plant growth is slow. Rate of growth then increases rapidly during the exponential phase. After some time the growth rate slowly decreases due to limitation of nutrient. This phase constitutes the stationary phase . The terms 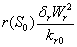 and
and 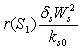 are taken to account for the diminishing growth phase and stationary phase in the plant growth dynamics. Where,
are taken to account for the diminishing growth phase and stationary phase in the plant growth dynamics. Where, 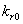 is the maximum root dry weight.
is the maximum root dry weight. 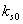 is the maximum shoot dry weight.
is the maximum shoot dry weight. 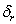 and
and 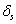 are nutrient limiting coefficients.
are nutrient limiting coefficients. 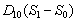 and
and 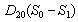 represent the flux of nutrient from shoot to root and root to shoot respectively. Where,
represent the flux of nutrient from shoot to root and root to shoot respectively. Where, 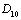 and
and 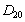 are transfer rates.
are transfer rates. 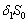 represents the loss of nutreint due to leaching.
represents the loss of nutreint due to leaching. 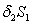 represent the loss of nutrient due shedding of leaves.
represent the loss of nutrient due shedding of leaves. 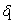 is leaching rate and
is leaching rate and 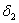 is natural decay rate of
is natural decay rate of 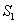 .Model 2 (Model with toxic effect):In this model, the effect of toxic metal on plant growth dynamics is considered. Here, we assume that the nutrient concentration and dry weight are adversely effected by toxic heavy metal. Let
.Model 2 (Model with toxic effect):In this model, the effect of toxic metal on plant growth dynamics is considered. Here, we assume that the nutrient concentration and dry weight are adversely effected by toxic heavy metal. Let 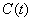 is the concentration of toxic metal in soil and
is the concentration of toxic metal in soil and 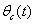 is the concentration of toxic metal adsorbed on the surface of soil. After incorporating the stress of toxic metal in the model 1 with the assumptions mentioned earlier in section 1, we get the following model 2:
is the concentration of toxic metal adsorbed on the surface of soil. After incorporating the stress of toxic metal in the model 1 with the assumptions mentioned earlier in section 1, we get the following model 2: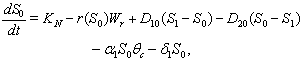 | (7) |
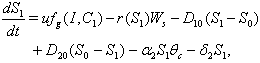 | (8) |
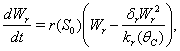 | (9) |
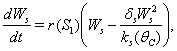 | (10) |
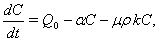 | (11) |
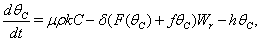 | (12) |
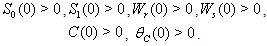 Here, we assume the following forms for
Here, we assume the following forms for 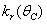 ,
, 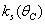 and uptake function
and uptake function 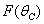 [25]:
[25]: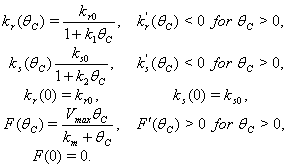 | (13) |
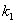 ,
, 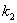 ,
, 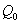 ,
, 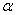 ,
, 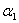 ,
, 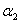 ,
, 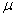 ,
, 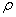 ,
, 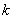 ,
, 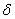 ,
, 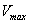 ,
, 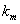 ,
, 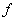 and
and 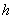 , which are described as follows:
, which are described as follows: 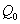 is the input rate of heavy metals.
is the input rate of heavy metals. 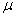 is the first order rate constant.
is the first order rate constant. 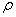 is the soil bulk density.
is the soil bulk density. 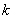 is the linear adsorption and absorption coefficient.
is the linear adsorption and absorption coefficient. 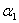 and
and 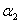 are decreasing rates of
are decreasing rates of 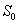 and
and 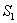 respectively due to
respectively due to 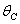 .
.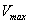 is the maximum uptake rate of
is the maximum uptake rate of 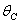 .
. 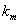 is the Michaelis-Menten constant.
is the Michaelis-Menten constant. 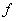 is the first order rate coefficient.
is the first order rate coefficient. 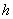 is the natural decay rate of
is the natural decay rate of 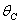 due to soil depletion on account of natural process.
due to soil depletion on account of natural process. 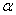 is natural decay rate of
is natural decay rate of 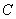 . Here, all the parameters
. Here, all the parameters 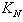 ,
, 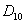 ,
, 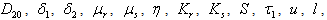
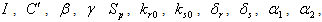
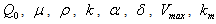 and
and 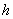 are taken to be positive constants.
are taken to be positive constants.3. Boundedness and Dynamical Behaviour
3.1. Analysis of Model 1
- Now, we show that the solutions of the model given by (1) to (4) are bounded in a positive orthant in
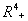 . The boundedness of solutions is given by the following lemma.Lemma 3.1: All the solutions of model will lie in the region
. The boundedness of solutions is given by the following lemma.Lemma 3.1: All the solutions of model will lie in the region 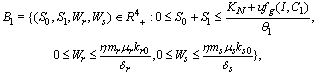 as
as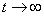 , for all positive initial values
, for all positive initial values 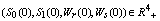 ,where
,where 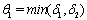 .Proof: By adding Eqs. (1) and (2), we get,
.Proof: By adding Eqs. (1) and (2), we get, 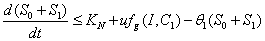 where,
where,  and then by the usual comparison theorem we get as
and then by the usual comparison theorem we get as 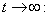
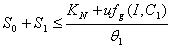 From Eq. (3), we get,
From Eq. (3), we get, 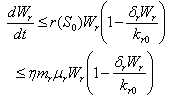 if
if 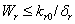 and then by the usual comparison theorem we get as
and then by the usual comparison theorem we get as 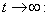
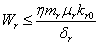 Similarly from Eq. (4), we get,
Similarly from Eq. (4), we get, 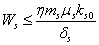 This complete the proof of lemma.Now we show the existence of the interior equilibrium
This complete the proof of lemma.Now we show the existence of the interior equilibrium 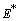 of Model 1. The system of equations (1) - (4) has one feasible equilibria
of Model 1. The system of equations (1) - (4) has one feasible equilibria 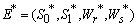 . The equilibrium
. The equilibrium 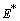 of the system is obtained by solving the following equations,
of the system is obtained by solving the following equations, 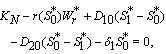 | (14) |
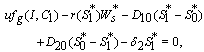 | (15) |
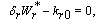 | (16) |
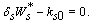 | (17) |
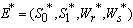 , where,
, where, 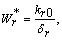 | (18) |
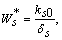 | (19) |
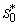 and
and 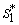 can be obtained by solving the following pair of equations:
can be obtained by solving the following pair of equations: 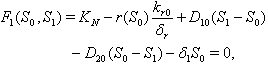 | (20) |
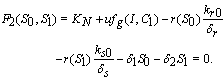 | (21) |
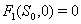 implies
implies 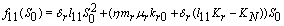
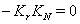 ,2.
,2. 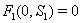 implies
implies 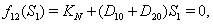 3.
3. 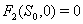 implies
implies 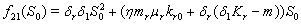
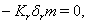 4.
4. 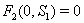 implies
implies 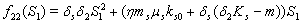
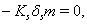 where,
where, 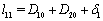 and
and 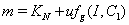 .The two Eqs. (20) and (21) intersect each other in the positive phase plane satisfying
.The two Eqs. (20) and (21) intersect each other in the positive phase plane satisfying 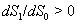 for Eq. (20) and
for Eq. (20) and 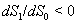 for Eq. (21), showing the existence of the unique interior equilibrium
for Eq. (21), showing the existence of the unique interior equilibrium 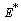 .From Eq. (15) as
.From Eq. (15) as 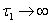 :
: 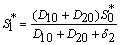 | (22) |
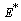 of the model given by (1)-(4) and for this local and global stability analysis have been carried out subsequently.The characteristic equation associated with the variational matrix about equilibrium
of the model given by (1)-(4) and for this local and global stability analysis have been carried out subsequently.The characteristic equation associated with the variational matrix about equilibrium 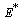 is given by
is given by 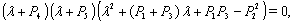 | (23) |
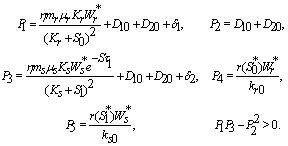 From the nature of the roots of the characteristic equation (23) we derive that the equilibrium point
From the nature of the roots of the characteristic equation (23) we derive that the equilibrium point 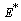 is always locally asymptotically stable.Now, we discuss the global stability of the interior equilibrium point
is always locally asymptotically stable.Now, we discuss the global stability of the interior equilibrium point 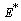 of the system (1)-(4). The non-linear stability of the interior positive equilibrium is determined by the following theorem.Therorem 3.2: In addition to assumptions (6), let
of the system (1)-(4). The non-linear stability of the interior positive equilibrium is determined by the following theorem.Therorem 3.2: In addition to assumptions (6), let 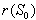 and
and 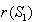 , satisfy in
, satisfy in 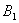
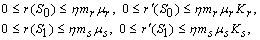 | (24) |
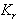 and
and 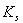 less than 1. Then if the following inequalities hold
less than 1. Then if the following inequalities hold 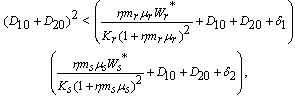 | (25) |
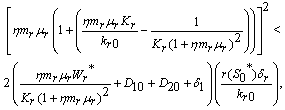 | (26) |
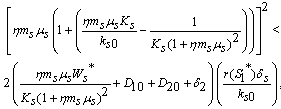 | (27) |
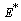 is globally asymptotically stable with respect to solutions initiating in the interior of the positive orthant. Proof: Since
is globally asymptotically stable with respect to solutions initiating in the interior of the positive orthant. Proof: Since 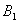 is an attracting region, and does not contain any invariant sets on the part of its boundary which intersect in the interior of
is an attracting region, and does not contain any invariant sets on the part of its boundary which intersect in the interior of 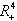 , we restrict our attention to the interior of
, we restrict our attention to the interior of 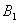 . We consider a positive definite function about
. We consider a positive definite function about 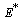
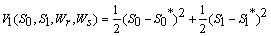
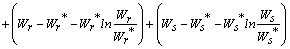 Then the derivatives along solutions,
Then the derivatives along solutions, 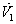 is given by
is given by 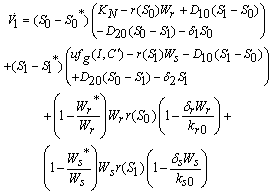 After some algebraic manipulations, this can be written as
After some algebraic manipulations, this can be written as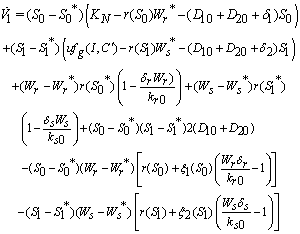 Where,
Where,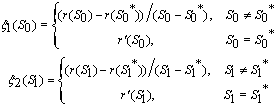 We note from (24) and the mean value theorem, that
We note from (24) and the mean value theorem, that 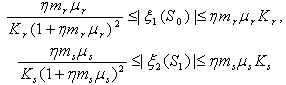 We know that
We know that 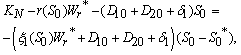
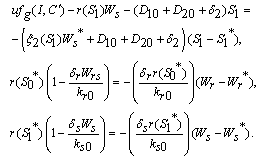 Hence
Hence  can be written as the sum of three quadratic forms,
can be written as the sum of three quadratic forms,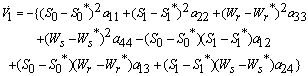 Where,
Where, 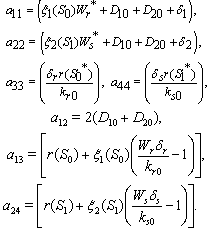 By Sylvester’s criteria we find that
By Sylvester’s criteria we find that 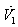 is negative definite if
is negative definite if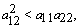 | (28) |
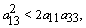 | (29) |
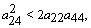 | (30) |
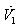 is negative definite and so
is negative definite and so 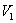 is a Liapunov function with respect to
is a Liapunov function with respect to 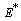 , whose domain contains
, whose domain contains 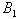 , proving the theorem.The above theorem shows, that provided inequalities (25) to (27) hold, the system settles down to a steady state solution.
, proving the theorem.The above theorem shows, that provided inequalities (25) to (27) hold, the system settles down to a steady state solution.3.2. Analysis of Model 2
- Now, in the following we show that the solutions of model given by (7) to (12) are bounded in a positive orthant in
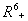 . The boundedness of solutions is given by the following lemma.Lemma 3.3: All the solutions of model will lie in the region
. The boundedness of solutions is given by the following lemma.Lemma 3.3: All the solutions of model will lie in the region 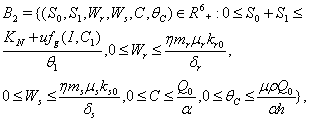 as
as 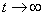 , for all positive initial values
, for all positive initial values 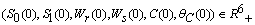 , where
, where 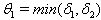 . Proof: By adding Eqs. (7) and (8), we get,
. Proof: By adding Eqs. (7) and (8), we get, 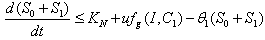 where,
where, 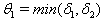 and then by the usual comparison theorem we get as
and then by the usual comparison theorem we get as 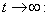
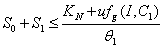 From Eq. (9), we get,
From Eq. (9), we get, 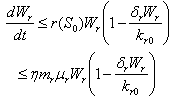 if
if 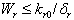 and then by the usual comparison theorem we get as
and then by the usual comparison theorem we get as 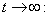
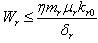 Similarly from Eq. (10), we get,
Similarly from Eq. (10), we get, 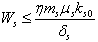 From Eq. (11), we get,
From Eq. (11), we get, 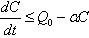 Then by the usual comparison theorem we get as
Then by the usual comparison theorem we get as 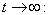
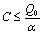 From Eq. (12), we get,
From Eq. (12), we get, 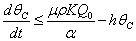 Then by the usual comparison theorem we get as
Then by the usual comparison theorem we get as 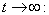
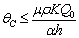 This complete the proof of lemma.Now, we find the interior equilibrium
This complete the proof of lemma.Now, we find the interior equilibrium 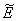 of Model 2. The system of equations (7) - (12) has one feasible equilibria
of Model 2. The system of equations (7) - (12) has one feasible equilibria 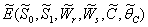 . The equilibrium
. The equilibrium 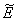 of the system is obtained by solving the following equations,
of the system is obtained by solving the following equations, 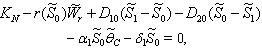 | (31) |
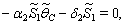 | (32) |
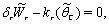 | (33) |
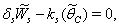 | (34) |
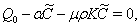 | (35) |
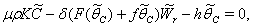 | (36) |
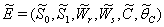 , where,
, where, 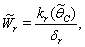 | (37) |
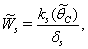 | (38) |
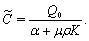 | (39) |
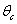 increases.The
increases.The 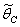 is given by the positive root of the equation
is given by the positive root of the equation 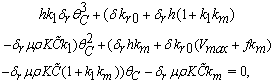 | (40) |
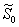 and
and 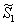 can be obtained by solving the following pair of equations:
can be obtained by solving the following pair of equations: 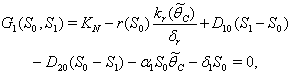 | (41) |
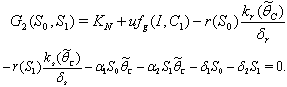 | (42) |
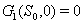 implies
implies 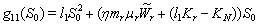
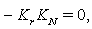 2.
2. 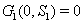 implies
implies 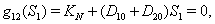 3.
3. 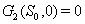 implies
implies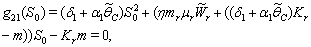 4.
4. 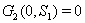 implies
implies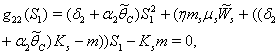 where,
where, 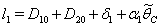 and
and 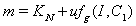 .The two Eqs. (41) and (42) intersect each other in the positive phase plane satisfying
.The two Eqs. (41) and (42) intersect each other in the positive phase plane satisfying 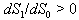 for Eq. (41) and
for Eq. (41) and 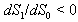 for Eq. (42), showing the existence of the unique interior equilibrium
for Eq. (42), showing the existence of the unique interior equilibrium 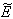 .From Eq. (32) as
.From Eq. (32) as 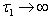 :
: 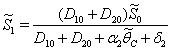 | (43) |
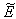 of the model given by (7)-(12) and for this local and global stability analysis have been carried out subsequently.The characteristic equation associated with the variational matrix about equilibrium
of the model given by (7)-(12) and for this local and global stability analysis have been carried out subsequently.The characteristic equation associated with the variational matrix about equilibrium 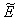 is given by
is given by 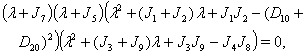 | (44) |
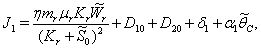
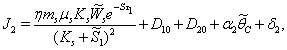
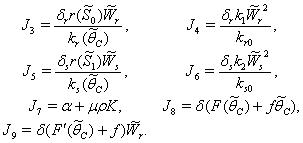 From the nature of the roots of the characteristic equation (44) we derive that the equilibrium point
From the nature of the roots of the characteristic equation (44) we derive that the equilibrium point 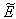 is locally stable if
is locally stable if 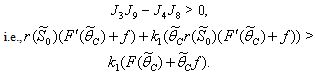 | (45) |
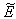 of the system (7)-(12). The non-linear stability of the interior positive equilibrium state is determined by the following theorem.Therorem 3.4: In addition to assumptions (6) and (13), let
of the system (7)-(12). The non-linear stability of the interior positive equilibrium state is determined by the following theorem.Therorem 3.4: In addition to assumptions (6) and (13), let 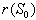 ,
, 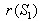 ,
, 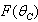 ,
, 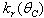 and
and 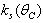 satisfy in
satisfy in 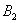
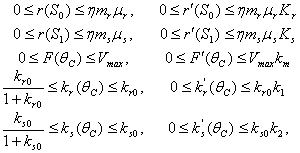 | (46) |
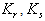 and
and 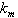 less than 1. Then if the following inequalities hold
less than 1. Then if the following inequalities hold 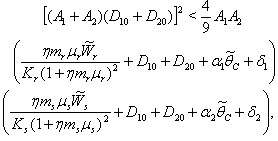 | (47) |
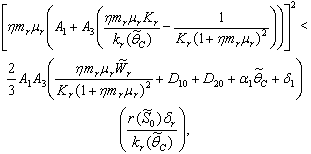 | (48) |
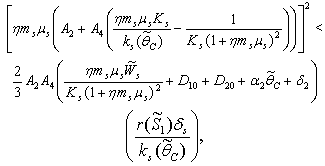 | (49) |
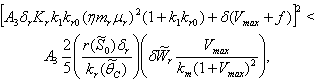 | (50) |
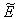 is globally asymptotically stable with respect to solutions intiating in the interior of the positive orthant. Proof: Since
is globally asymptotically stable with respect to solutions intiating in the interior of the positive orthant. Proof: Since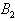 is an atttracting region, and does not contain any invariant sets on the part of its boundary which intersect in the interior of
is an atttracting region, and does not contain any invariant sets on the part of its boundary which intersect in the interior of 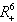 , we restrict our attention to the interior of
, we restrict our attention to the interior of 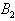 .We consider a positive definite function about
.We consider a positive definite function about 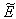
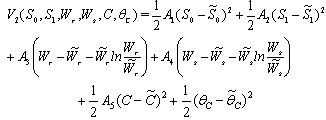 where,
where, 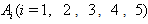 are arbitrary positive constants. Then the derivatives along solutions, is given by After some algebraic manipulations, this can be written as
are arbitrary positive constants. Then the derivatives along solutions, is given by After some algebraic manipulations, this can be written as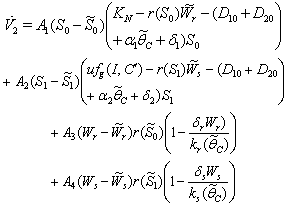
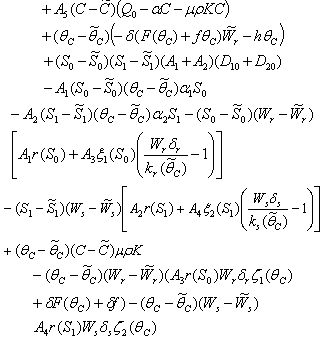 Where
Where We note from (46) and the mean value theorem, that
We note from (46) and the mean value theorem, that 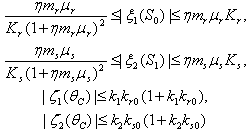 and
and 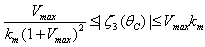 .We know that
.We know that 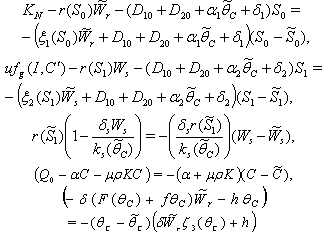 Hence
Hence 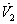 can be written as the sum of three quadratic forms
can be written as the sum of three quadratic forms 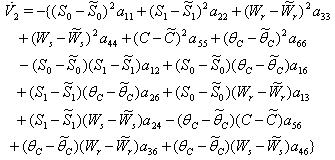 where
where 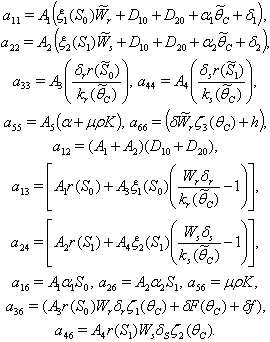 By Sylvester’s criteria we find that
By Sylvester’s criteria we find that 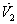 is negative definite if
is negative definite if 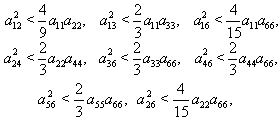 | (51) |
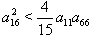 ,
, 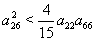 ,
, 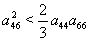 and
and 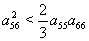 are satisfied due to arbitrary choice of
are satisfied due to arbitrary choice of 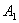 ,
, 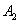 ,
, 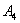 and
and 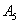 respectively, and above conditions reduces to the following conditions:
respectively, and above conditions reduces to the following conditions: 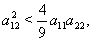 | (52) |
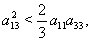 | (53) |
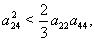 | (54) |
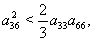 | (55) |
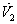 is negative definite and so
is negative definite and so 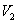 is a Liapunov function with respect to
is a Liapunov function with respect to 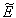 , whose domain contains
, whose domain contains 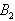 , proving the theorem.The above theorem shows, that provided inequalities (47) to (50) hold, the system settles down to a steady state solution.
, proving the theorem.The above theorem shows, that provided inequalities (47) to (50) hold, the system settles down to a steady state solution.4. Numerical Example
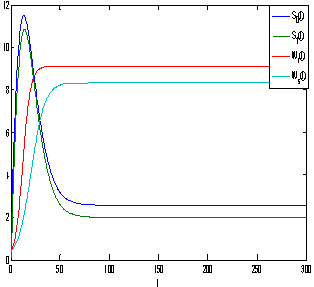
- For the model 1, consider the following values of parameters-
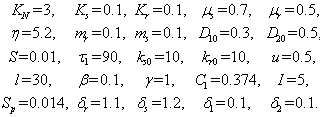 For the above set of parametric values, we obtain the following values of interior equilibrium point
For the above set of parametric values, we obtain the following values of interior equilibrium point 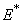 -
-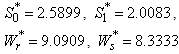 which is asymptotically stable (see Figure 1).Further, to illustrate the global stability of interior equilibrium
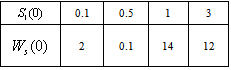
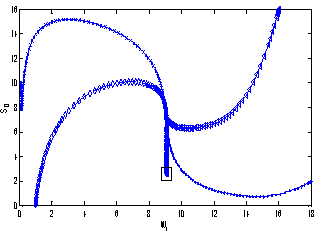
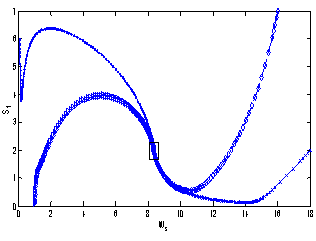
which is asymptotically stable (see Figure 1).Further, to illustrate the global stability of interior equilibrium 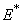 of model 1 graphically, numerical simulation is performed for different initial conditions (see Table 1 and 2) and results are shown in Figures 2 and 3 for
of model 1 graphically, numerical simulation is performed for different initial conditions (see Table 1 and 2) and results are shown in Figures 2 and 3 for 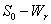 phase plane and
phase plane and 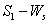 phase plane respectively. All the trajectories are starting from different initial conditions and reach to interior equilibrium
phase plane respectively. All the trajectories are starting from different initial conditions and reach to interior equilibrium 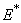 .
. | Figure 1. Trajectories of the model 1 with respect to time (with no toxic effect) showing the stability behaviour |
|
|
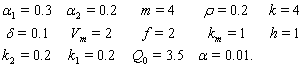 we obtain the following values of interior equilibrium point
we obtain the following values of interior equilibrium point 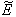 as
as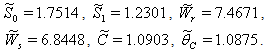 For the set of parametric values considered, the stability conditions given in Eq. (45) and Eqs. (47)-(50) are satisfied. Hence,
For the set of parametric values considered, the stability conditions given in Eq. (45) and Eqs. (47)-(50) are satisfied. Hence, 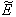 is asymptotically stable (see Figure 4).
is asymptotically stable (see Figure 4).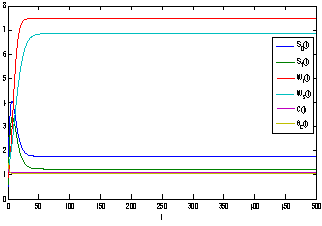 | Figure 4. Trajectories of the model 2 with respect to time (with toxic effect) showing the stability behaviour |
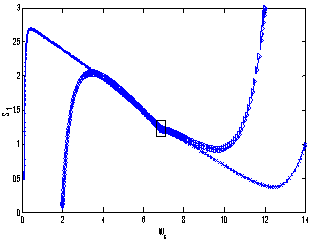
 of model 2 graphically, numerical simulation is performed for different initial conditions (see Table 3 and 4) and results are shown in Figures 5 and 6 for
of model 2 graphically, numerical simulation is performed for different initial conditions (see Table 3 and 4) and results are shown in Figures 5 and 6 for 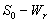 phase plane and
phase plane and 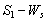 phase plane respectively. All the trajectories are starting from different initial conditions and reach to interior equilibrium
phase plane respectively. All the trajectories are starting from different initial conditions and reach to interior equilibrium 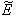
|
|
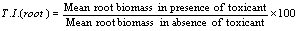

5. Conclusions
- Equilibrium
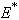 of model 1 is shown to be asymptotically stable (see Fig. 1). The equilibria
of model 1 is shown to be asymptotically stable (see Fig. 1). The equilibria  of model 2 is shown to be asymptotically stable (see Fig. 4). From Figures 7(a) and 7(b), it may be noted that the equilibrium levels of nutrient concentrations in each compartment with no toxic effect are more than that of the equilibrium levels of nutrient concentrations in respective compartments when toxic effect is considered.
of model 2 is shown to be asymptotically stable (see Fig. 4). From Figures 7(a) and 7(b), it may be noted that the equilibrium levels of nutrient concentrations in each compartment with no toxic effect are more than that of the equilibrium levels of nutrient concentrations in respective compartments when toxic effect is considered. 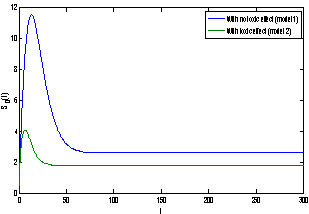 | Figure 7(a). Graph between nutrient concentration in root S0 and time t for model 1(with no toxic effect) and for model 2(with toxic effect) |
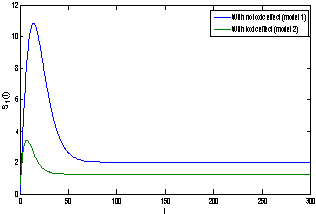 | Figure 7(b). Graph between nutrient concentration in shoot S1 and time t for model 1(with no toxic effect) and for model 2(with toxic effect) |
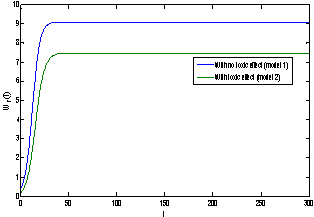 | Figure 8(a). Graph between root dry weight Wr and time t for model 1 (with no toxic effect) and for model 2(with toxic effect) |
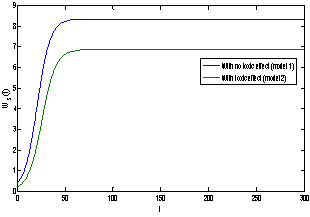 | Figure 8(b). Graph between shoot dry weight Ws and time t for model 1(with no toxic effect) and for model 2(with toxic effect) |
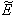 and tolerance indices (Table 5), it is concluded that the root dry weight and shoot dry weight decrease as the input rate of toxic metal
and tolerance indices (Table 5), it is concluded that the root dry weight and shoot dry weight decrease as the input rate of toxic metal 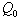 increases till
increases till 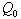 is less than or equal to
is less than or equal to 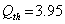 and upto this value the stability criteria is also preserved. Further, in case if
and upto this value the stability criteria is also preserved. Further, in case if 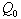 increases from its threshold value
increases from its threshold value 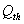 then the stability condition given by Eq. (45) is voilated and equilibrium
then the stability condition given by Eq. (45) is voilated and equilibrium 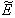 loses its stability. From the expressions (37) and (38) it may be noted that the root dry weight and shoot dry weight will decrease and may tend to zero with increasing
loses its stability. From the expressions (37) and (38) it may be noted that the root dry weight and shoot dry weight will decrease and may tend to zero with increasing 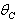 . From Eqs. (22) and (43), it is concluded that for large
. From Eqs. (22) and (43), it is concluded that for large 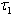 , the nutrient concentration in shoot with toxic effect is less than that of nutrient concentration in shoot when no toxic effect is considered. The Figures 9(a) and 9(b) represent the dynamical behaviour of the of root dry weight and shoot dry weight with respect to
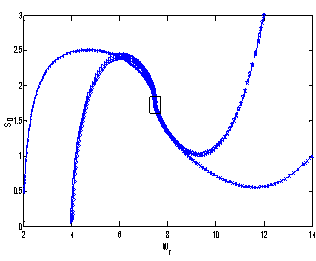
, the nutrient concentration in shoot with toxic effect is less than that of nutrient concentration in shoot when no toxic effect is considered. The Figures 9(a) and 9(b) represent the dynamical behaviour of the of root dry weight and shoot dry weight with respect to 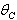 . From these figures it is observed that the toxicity of the metal will adversely effect the plant growth in its early stages resulting in loss of crop productivity[8],[29].
. From these figures it is observed that the toxicity of the metal will adversely effect the plant growth in its early stages resulting in loss of crop productivity[8],[29].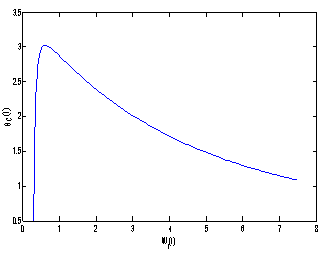 | Figure 9(a). Phase Plane Graph of root dry weight Wr and θC for model 2 |
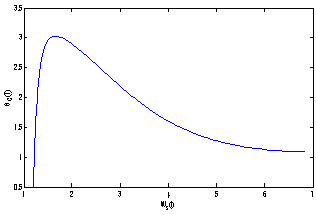 | Figure 9(b). Phase Plane Graph of shoot dry weight Wr and θC for model 2 |
References
| [1] | R. Tucker, D.H. Hardy, C.E. Stokes, Heavy Metals in North Carolina Soils, Occurance and Significance, N.C. Department of Agriculture and Consumer Services, Agronomics division, Raleigh, 2003. |
| [2] | R.H. Merry, K.G. Tiller, A.M. Alston, The Effects of Contamination of Soil with Copper, lead, Mercury and Arsenic on the Growth and Composition of Plants. Effects of Season, Genotype, Soil Temperature and Fertilizers, Plant Soil, Vol. 91, 115-128, 1986. |
| [3] | A. Brune, K. J. Dietz, A Comparative Analysis of Element Composition of Roots and Leaves of Barley Seedlings Grown in the Presence of Toxic Cadmium, Molybdenum, Nickel and zinc Concentration, J. Plant. Nutr, Vol. 18, 853-868, 1985. |
| [4] | V. N. Pishchik, N. I. Vorobyev, I. I. Chernyaeva, S. V. Timofeea, A. P. Kozhemyakov, Y. V. Alexeev, S. M. Lukin, Experimental and Mathematical Simulation of Plant Growth Promoting Rhizobacteria and Plant Interaction under Cadmium Stress, Plant and Soil, Vol. 243, 173-186, 2002. |
| [5] | L.S.D. Toppi, R. Gabbrielli, Response to Cadmium in hHgher Plants, Environ. Exp. Bot., Vol. 41, No. 2, 105-130, 1999. |
| [6] | S. Trivedi, L. Erdei, Effects of Cadmium and lead on the Aaccumulation of Ca2+and K+ and on the Influx and Ttranslocation of K+ Status, Physiol. Plant, Vol. 84, 94-100, 1992. |
| [7] | Misra, O. P., Sinha P., Rathore, S. K. S., 2008, Effect of Polluted Soil on the Growth Dynamics of Plant-Herbivour System: A Mathematical Model, Proc. Nat. Acad. Sci. India Sect, Vol. A 78, Pt.II. |
| [8] | S. Faizan, S. Kuusar, R. Perveen, Varietal Difference for Cadmium-induced Seedling Mortality, Foliar Toxicity Symptoms. Plant Growth, Proline and Nitrate Reductase Activity in Chickpea(Cicer Arietinum L), Biology and Medicine, Vol. 3, 196-206, 2011. |
| [9] | K. Padmaja, D.D.K. Prasad, A.R.K. Prasad, Inhibition of Chlorophyll synthesis in Phaseolus Vulgrais Seedlings by Cadmium Acetate Photosynthetica, Vol. 24, 399-405, 1990. |
| [10] | L.M. Sandalio, H.C. Dalurzo, M. Gomez, M. C. Romero-Puertas, L.A. Del Rio, Cadmium-induced Changes in the Growth and Oxidative Metabolism of Pea Plants. Journal of Experimental Botony, Vol. 52, 2115-2126, 2001. |
| [11] | R.T. Guo, G.P. Zhang, W.Y. Lu, H.P. Wu, , F.B. Wu, J.X. Chen, J.X. Zhou, Effect of Al on dry matter accumulation and Al and nutrients in barleys differing in Al tolerance, Plant Nutr. Fert. Sci., Vol. 9, No. 3, 324-330 2003. |
| [12] | S. Burzynski, K. Mereck, Effect of Pb and Cd on Enzymes of Nitrate Assimilation in Cucumber Seedling, Acta Physiology Plants, Vol. 12, 105-110, 1990. |
| [13] | L.I.U. Hailing, L.I. Qing, Y. Ping, Effects of Cadmium on Seed Germination, Seddling Growth and Oxidase Eenzyme in Crops, Chinese Journal of Environmental Science, Vol. 12, 29-31, 1991. |
| [14] | M.Z. Iqbal, D. A. Siddiqui, Effects of Lead Toxicity on Seed Germination and Seedling Growth of Some Tree Species, Pakistan Journal of Scientific and Industrial Research, Vol. 35, 139-141, 1992. |
| [15] | D.N. Singh, Srivastava, Effects of Cadmium on Seed Germination and Seedling Growth of Zea Mays, Biol. Sci., Vol. 61, 245-247, 1991. |
| [16] | Brown, M.T., Wilkins, D.A., 1986, The Effect of Zinc on Germination, Survival and Growth of Betula (Series A), Vol. 41, 53-61. |
| [17] | Morzeck, J.R.E., Funicelli, N.A., 1982, Effect of Zinc and Lead on Geermination of Spartina Alterniflora Loisel., Seeds at Various Salinities, Env. Exp. Bot. , Vol. 22, 23-32. |
| [18] | Safiq, M., Iqbal, M.Z., 2005, The Toxicity Effects of Heavy Metals on Germination and Seedling Growth of Cassia Siamea Lamark, Journal of New Seeds, Vol. 7, 95-105. |
| [19] | Leo, G.D, Furia, L.D., Gatto, M., 1993, The Interaction Between Soil Acidity and Forest Dynamics: A Simple Model Exhibiting Catastrophic Behavior, Theoretical Population Biology, Vol. 43, 31-51. |
| [20] | Verma, P., Georage, K. V., Singh, H. V., Singh, R. N., 2007, Modeling Cadmium Accumulation in Radish, Carrot, Spinch and Cabbage, Applied Mathematical Modelling, Vol. 31, 1652-1661. |
| [21] | L. J. Gross, Mathematical Modelling in Plant Biology: Implications of Physiological Approaches for Resource Management, Third Autumn Course on Mathematical Ecology, (International Center for Theoretical Physics, Trieste, Italy), 1990. |
| [22] | J.H.M. Thornley, Mathematical Models in Plant Physiology, Academic Press, NY, 1976. |
| [23] | L. R. Benjamin, R. C. Hardwick, Sources of Variation and Measures of Variability in Even-Aged Stands of Plants, Ann. Bot., Vol. 58, 757-778, 1986. |
| [24] | A. Pugliese, Optimal Resource Allocation in Perennial Plants: A Continuous-Time model, Theoretical Population Biology, Vol. 34, No. 3, 1988. |
| [25] | F. Somma, J.W. Hopmans, V. Clausnitzer, Transient Three-Dimensionl Modelling of Soil Water and Solut Transport with Simultaneous root Growth, Root Water and Nutrient Uptake, Plant and soil, Vol. 202, 281-293, 1998. |
| [26] | Ittersum, M. K. V., Leffelaar, P.A., Keulen, H. V., Kropff, M. J., Bastiaans, L., Goudriaan, J., 2002, Developments in Modelling Crop Growth, Cropping Systems and Production Systems in the Wageningen School, NJAS 50 . |
| [27] | Dercole, F., Niklas, K., Rand, R., 2005, Self-Thinning and Community Persistance in a Simple Size-Structure Dynamical Model of Plant Growth, J. Math. Biol, Vol. 51, 333-354. |
| [28] | DeAngelis, D. L., Gross, L.J., 1992, Individual Based Models and Approaches in Ecology : Populations, Communities and Ecosystems, Chapman and Hall, New York, London. |
| [29] | Kabir, M., Zafar Iqbal, M., Shafiq, M., Farooqi, Z.R., 2008, Reduction in Germination and Seedling Growth of Thespesia Populena L., Caused by Lead and Cadmium Treatments, Pak. J. Bit., Vol. 40, 2419-2426. |
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML and
and  of model 1
of model 1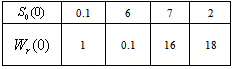
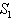 and
and 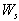 of model 1
of model 1