Arun Kumar Gupta1, Pragati Sharma2
1Department of Mathematics, M.S. College, Saharanpur, U.P., India
2Department of Mathematics, H.C.T.M., Kaithal, Haryana, India
Correspondence to: Arun Kumar Gupta, Department of Mathematics, M.S. College, Saharanpur, U.P., India.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
The goal of present investigation is to study the effect of thermal gradient on the vibrations of non-homogeneous trapezoidal plate whose thickness varies parabolically and density varies linearly. Effect of other plate parameters such as non-homogeneity constant, taper constant and aspect ratios have also been studied. C-S-C-S boundary condition with two term deflection is taken into consideration. Rayleigh-Ritz method is used to find the solution of the problem. Results are calculated with great accuracy and presented in tabular form. Comparison of the results with published data has also shown.
Keywords:
Vibration, Trapezoidal Plate, Thermal Gradient, Non-Homogeneity, Parabolically Varying Thickness
Cite this paper:
Arun Kumar Gupta, Pragati Sharma, "Study of Thermally Induced Vibration of Non-Homogeneous Trapezoidal Plate with Varying Thickness and Density", American Journal of Computational and Applied Mathematics, Vol. 2 No. 6, 2012, pp. 265-275. doi: 10.5923/j.ajcam.20120206.05.
1. Introduction
Thermal effect on vibration of non-homogenous plates are of great interest in the field of engineering such as for better designing of gas turbines, jet engine, space craft and nuclear power projects. Such structures are exposed to high intensity heat fluxes and thus material properties undergo significant changes, in particular the thermal effect on the modules of elasticity of the material can not be taken as negligible. Plates of variable thickness are frequently used in order to economize the plate material or to lighten the plates, especially when it is used in the wings of high-speed and high performance aircrafts. The study of vibration of plates has acquired great importance in the field of research, engineering and space technology. In the engineering we cannot move without considering the effect of vibration because almost machines and engineering structuresexperiences vibrations. Structures of plates have wide applications in ships, bridges etc. In the aeronautical field, analysis of thermally induced vibrations in non-homogeneous plates of variable thickness has a great interest due to their utility in aircraft wings.Many analyses show that plate vibrations are based on non-homogeneity of materials. Non-homogeneity can be natural or artificial. Non-homogeneous materials such as plywood, delta wood, fibre-reinforced plastic etc, are used in engineering design and technology to strengthen the construction. Study of the effect of vibration cannot be restricted only in the field of science but, our day to day life is also affected by it. Vibration of plates of various shapes, homogeneous or non-homogeneous, orthotropic or isotropic, with or without variation in thickness, have been studied by various authors, with or without considering the effect of temperature.A large number of researchers have reported about the vibration analysis of different types of plates. Some of them are mentioned here.Sharma et al.[1] studied the free transverse vibrations of non-homogeneous circular plates of linearly varying thickness. Gupta et al.[2] worked on the vibrations of non-homogeneous rectangular plate of variable thickness in both directions with thermal gradient effect. Gutierrez and Laura[3] calculated the fundamental frequency of vibrating rectangular, non-homogeneous plates. Gupta and Kumar[4] studied the effect of thermal gradient on free vibration of non-homogeneous visco-elastic rectangular plate of parabolically varying thickness.Gupta et al.[5] observed the transverse vibration of non-homogeneous orthotropic visco-elastic circular plate of varying parabolic thickness. Lal et al [6] studied the transverse vibrations of non-homogeneous rectangular plates of uniform thickness using boundary characteristic orthogonal polynomials. Gupta et al.[7] observed the effect of non-homogeneity on the free vibrations of orthotropic visco-elastic rectangular plate of parabolic varying thickness. Gupta and Kumar[8] studied the thermal effect on vibration of non-homogenous visco-elastic rectangular plate of linear varying thickness. Gupta et al.[9] worked on the vibration of visco-elastic orthotropic parallelogram plate with parabolically thickness variation. El-Sayad and Ghazy[10] studied the Rayleigh-Ritz method for free vibration of midline trapezoidal plates. Gupta and Kumar[11] did the free vibration analysis of non-homogeneous visco-elastic circular plate with varying thickness subjected to thermal gradient. Lal and Dhanpati[12] worked on the transverse vibrations of non-homogeneous orthotropic rectangular plates of variable thickness. Gupta et al.[13] did the vibration analysis of non-homogeneous circular plate of nonlinear thickness variation by differential quadrature method. Chakraverty et al.[14] noticed the effect of non-homogeneity on natural frequencies of vibration of elliptic plates. Chen et al[15] studied on free vibration of non-homogeneous transversely isotropic magneto-electro elastic plates. Gupta et al | Figure 1. Use of plates |
[16] observed the effect of non-homogeneity on vibration of orthotropic visco-elastic rectangular plate of linearly varying thickness. Gupta and Sharma[17] observed the effect of thermal gradient on transverse vibration of non-homogeneous orthotropic trapezoidal plate of parabolically varying thickness. Chen et al[18] studied the free vibration of cantilevered symmetrically laminated thick trapezoidal plates. Bambill et al.[19] studied the transverse vibrations of rectangular, trapezoidal and triangular orthotropic, cantilever plates. Gupta and Sharma[20] observed the thermally induced vibration of orthotropic trapezoidal plate of linearly varying thickness. Gurses et al.[21] analysed the shear deformable laminated composite trapezoidal plates. Kitipornchai et al.[22] discussed a global approach for vibration of thick trapezoidal plates. Gupta and Sharma[23] studied the thermal gradient effect on frequencies of a trapezoidal plate of linearly varying thickness. Gupta and Sharma[24] studied the thermal effect on vibration of non-homogeneous trapezoidal plate of linearly varying thickness. The authors have so far not come across any paper dealing with parabolically varying thickness and linearly varying density. In the present work the effect of non-homogeneity, taper constant, thermal gradient and aspect ratios has been studied. The frequencies for the first two modes of vibration are obtained for C-S-C-S non-homogeneous trapezoidal plate by Rayleigh-Ritz method. The authenticity and accuracy of numerical results of the present work has been verified with the authors published paper[25]. Results are presented in tabular form. Comparison of results has also been presented.
2. Theoretical Formulation
2.1. Geometry of the Plate
The plate under consideration is shown in figure 2 which is thin, symmetric and non-homogeneous trapezoidal plate. Here h0 is the maximum plate thickness occurring at the left edge and 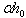 is the minimum plate thickness occurring at the right edge.
is the minimum plate thickness occurring at the right edge.
2.2. Thickness and Density
The thickness of the plate is parabolic in x direction and is of the form 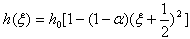 | (1) |
where h0 is thickness along the edge 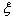 = x/a= -1/2. Non-homogeneity of plate arises due to variation in density which is linear in x direction and is of the form
= x/a= -1/2. Non-homogeneity of plate arises due to variation in density which is linear in x direction and is of the form 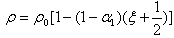 | (2) |
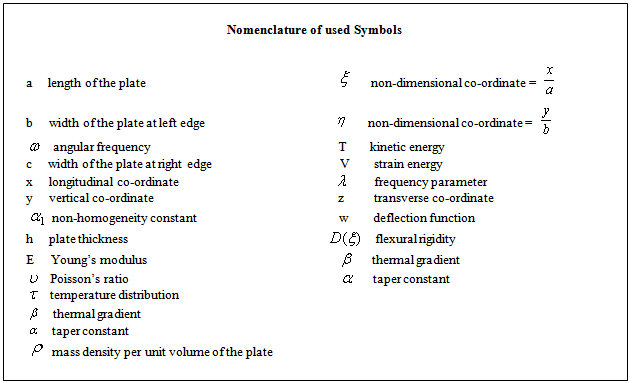
It is assumed that the plate considered here is subjected to a steady one-dimensional temperature distribution along the length i.e. in the x direction,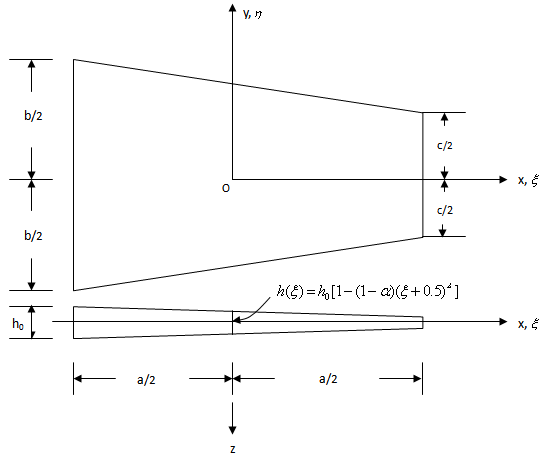 | Figure 2. Geometry of trapezoidal plate with variable thickness |
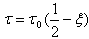 | (3) |
where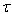 denotes the temperature excess above the reference temperature at a distance
denotes the temperature excess above the reference temperature at a distance 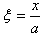 and
and 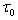 denotes the temperature excess above the reference temperature at the end
denotes the temperature excess above the reference temperature at the end 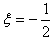 . For most of the elastic materials, modulus of elasticity is described as
. For most of the elastic materials, modulus of elasticity is described as 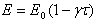 | (4) |
where E0 is the value of Young’s modulus along the reference temperature i.e. at 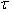 = 0 and
= 0 and 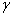 is the slope of the variation of E with
is the slope of the variation of E with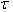 . On substituting value of
. On substituting value of 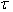 from equation (3) into (4)
from equation (3) into (4)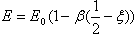 | (5) |
where 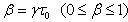 .
.
2.3. Equation of Motion
The governing differential equation for kinetic energy T and strain energy V is given by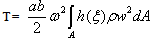 | (6) |
and 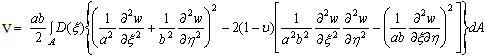 | (7) |
in which 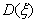 is the flexural rigidity of the plate, which is given by
is the flexural rigidity of the plate, which is given by 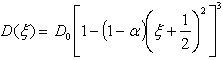 | (8) |
Also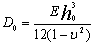 | (9) |
is the flexural rigidity of the plate at the side 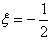 , A is the area of the plate and
, A is the area of the plate and 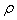 is the mass density per unit area of the plate.Using equation (9) and (5) in (8) flexural rigidity is given by
is the mass density per unit area of the plate.Using equation (9) and (5) in (8) flexural rigidity is given by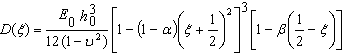 | (10) |
Using equation (10) in (7) & (1), (2) in (6)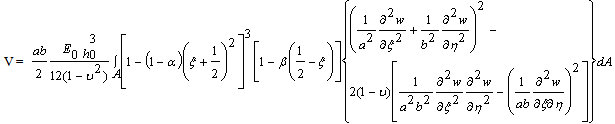 | (11) |
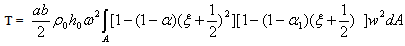 | (12) |
2.4. Deflection Function and Boundary Condition
A two term deflection function is taken as 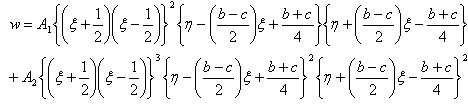 | (13) |
where A1 and A2 are constants to be evaluated. Eq. (13) satisfy boundary conditions and provide a good estimation to the frequency. Clamped-Simply supported-Clamped-Simply supported plate is taken into consideration as shown in figure.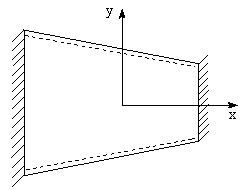 | Figure 3. C-S-C-S boundary condition of a trapezoidal plate |
Also for the plate considered here boundaries are defined by four straight lines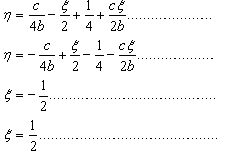 | (14) |
3. Method of Solution
Rayleigh-Ritz technique is used to find the solution of the problem. According to it maximum kinetic energy must be equal to maximum strain energy, so it is necessary for the problem under consideration that 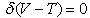 | (15) |
Using equation (14) in (11) and (12) 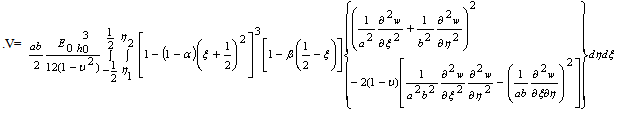 | (16) |
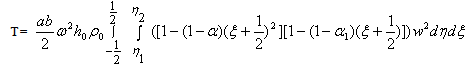 | (17) |
Now (15) becomes 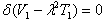 | (18) |
where  | (19) |
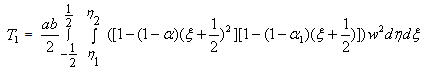 | (20) |
and 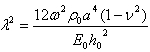 is a frequency parameter.Equation (18) involves the unknown A1 and A2 arising due to the substitution of
is a frequency parameter.Equation (18) involves the unknown A1 and A2 arising due to the substitution of 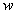 from eq (13). These two constants are to be determined from eq. (18), as follows
from eq (13). These two constants are to be determined from eq. (18), as follows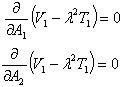 | (21) |
On simplifying (21), One gets 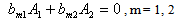 | (22) |
where 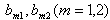 involve parametric constant and the frequency parameter.For a non-zero solution, it is desired that co-efficient of eq. (22) must be zero. So one gets the frequency equation as
involve parametric constant and the frequency parameter.For a non-zero solution, it is desired that co-efficient of eq. (22) must be zero. So one gets the frequency equation as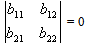 | (23) |
From eq. (23), one can obtain a quadratic equation in 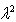 from which the two values can found which constitutes first and second mode of vibration.
from which the two values can found which constitutes first and second mode of vibration.
4. Results and Discussion
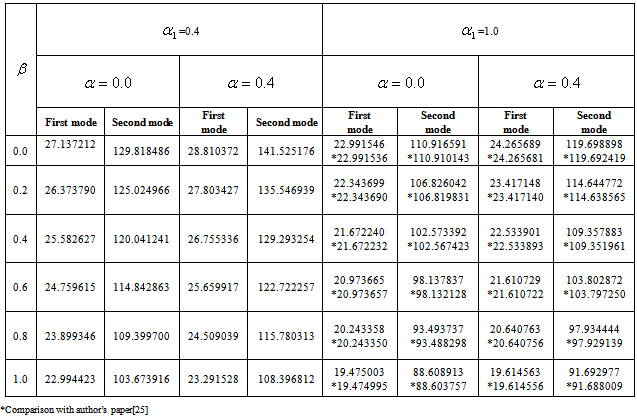
Frequencies for the first two modes of vibrations are computed for non-homogeneous trapezoidal plate whose thickness varies parabolically and density varies linearly. Different values of non-homogeneity constant (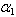 ), taper constant (
), taper constant (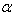 ), thermal gradient (
), thermal gradient (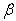 ) and aspect ratios (a/b, c/b) has been considered. All results are presented in tabular form.Table 1 and 2: These tables shows the effect of taper constant
) and aspect ratios (a/b, c/b) has been considered. All results are presented in tabular form.Table 1 and 2: These tables shows the effect of taper constant 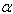 (0.0 to 1.0) on the frequency parameter
(0.0 to 1.0) on the frequency parameter 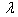 for
for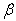 = 0.0, 0.4, = 0.4, 1.0, a/b = 1.0 and c/b = 0.5, 1.0.Table 3 and 4: These tables shows the behaviour of the frequency parameter
= 0.0, 0.4, = 0.4, 1.0, a/b = 1.0 and c/b = 0.5, 1.0.Table 3 and 4: These tables shows the behaviour of the frequency parameter 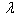 with thermal gradient
with thermal gradient 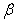 ( 0.0 to 1.0), for
( 0.0 to 1.0), for 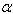 = 0.0, 0.4,
= 0.0, 0.4, 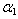 = 0.4, 1.0, a/b = 1.0 and c/b = 0.5, 1.0.Table 5, 6, 7 and 8: These tables show the effects of the frequency parameter
= 0.4, 1.0, a/b = 1.0 and c/b = 0.5, 1.0.Table 5, 6, 7 and 8: These tables show the effects of the frequency parameter 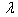 with aspect ratio c/b for different combinations of
with aspect ratio c/b for different combinations of 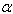 and
and 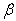 as follows.(i)
as follows.(i) 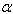 = 0.0,
= 0.0, 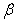 = 0.0(ii)
= 0.0(ii) 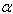 = 0.0,
= 0.0, 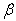 = 0.4(iii)
= 0.4(iii) 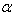 = 0.4,
= 0.4, 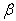 = 0.0(iv)
= 0.0(iv) 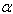 = 0.4,
= 0.4, 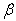 = 0.4.Non-homogeneity constant
= 0.4.Non-homogeneity constant 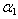 varies from 0.0 to 0.4, aspect ratio a/b varies from 0 .75 to 1.0 and aspect ratio c/b varies from 0.25 to 1.0.Table 9 and 10: In these tables effect of non-homogeneity constant (0.0 to 1.0) on frequency parameter has been shown. Four combinations of
varies from 0.0 to 0.4, aspect ratio a/b varies from 0 .75 to 1.0 and aspect ratio c/b varies from 0.25 to 1.0.Table 9 and 10: In these tables effect of non-homogeneity constant (0.0 to 1.0) on frequency parameter has been shown. Four combinations of 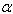 and
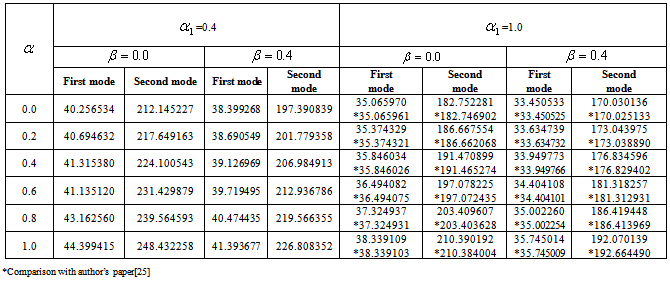
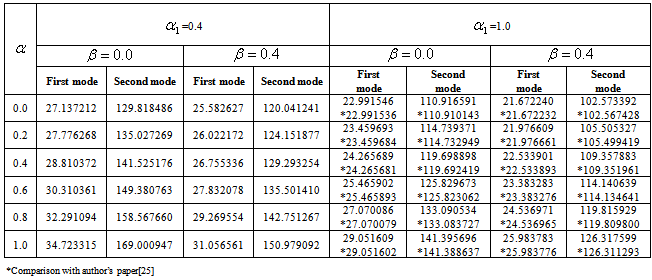
and 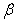 (as in table 5 to 8), two values of aspect ratio c/b (0.5, 1.0) and one value of aspect ratio a/b (1.0) has been taken. In table 1 and 2 it is observed that the frequency parameter
(as in table 5 to 8), two values of aspect ratio c/b (0.5, 1.0) and one value of aspect ratio a/b (1.0) has been taken. In table 1 and 2 it is observed that the frequency parameter 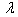 increases with increasing values of taper constant
increases with increasing values of taper constant 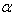 for both the modes of vibration. The rate of increase as well as the value of frequency parameter
for both the modes of vibration. The rate of increase as well as the value of frequency parameter 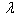 is higher in second mode in comparison to the first mode. Further on comparing the results of table 1 and 2 it is found that on increasing the value of aspect ratio c/b from 0.5 to 1.0, frequency parameter decreases for both the modes of vibration.In table 3 and 4 it is seen that frequency parameter
is higher in second mode in comparison to the first mode. Further on comparing the results of table 1 and 2 it is found that on increasing the value of aspect ratio c/b from 0.5 to 1.0, frequency parameter decreases for both the modes of vibration.In table 3 and 4 it is seen that frequency parameter 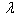 decreases with increasing values of thermal gradient
decreases with increasing values of thermal gradient 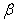 whatever be the values of other plate parameters. The rate of decrease as well as the value of frequency parameter
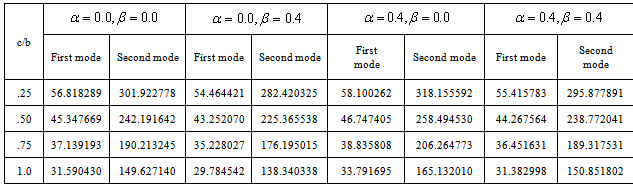
whatever be the values of other plate parameters. The rate of decrease as well as the value of frequency parameter 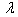 is higher in second mode in comparison to the first mode. Also on increasing aspect ratio c/b from 0.5 to 1.0, frequency parameter decreases for both the modes of vibration.It is noticed from table 5, 6, 7 and 8 that the frequency parameter
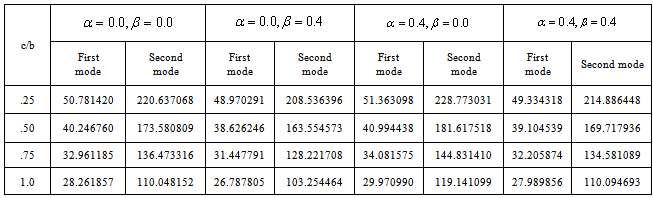
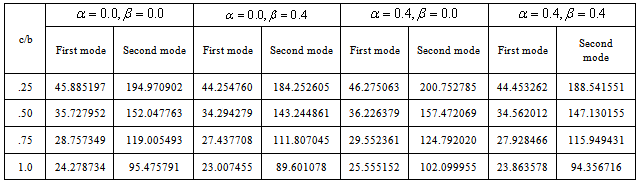
is higher in second mode in comparison to the first mode. Also on increasing aspect ratio c/b from 0.5 to 1.0, frequency parameter decreases for both the modes of vibration.It is noticed from table 5, 6, 7 and 8 that the frequency parameter 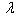 decreases with increasing values of aspect ratio c/b. Further if we compare table 5 and 6 (a/b = 0.75) it is found that the frequency parameter decreases with increase in non-homogeneity constant
decreases with increasing values of aspect ratio c/b. Further if we compare table 5 and 6 (a/b = 0.75) it is found that the frequency parameter decreases with increase in non-homogeneity constant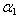 i.e. from 0.0 to 0.4. Similar pattern is observed on comparing table 7 and 8 (a/b = 1.0).Now if we compare table 5 and 7 in which aspect ratio a/b increased from 0.75 to 1.0 and non-homogeneity constant is 0.0. It is observed that frequency parameter increases for both the mode of vibration. Similar pattern is observed on comparing table 6 and 8 in which non-homogeneity constant is 0.4. Table 9 and 10 clearly shows that frequency parameter
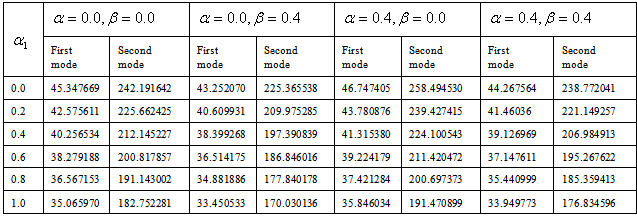
i.e. from 0.0 to 0.4. Similar pattern is observed on comparing table 7 and 8 (a/b = 1.0).Now if we compare table 5 and 7 in which aspect ratio a/b increased from 0.75 to 1.0 and non-homogeneity constant is 0.0. It is observed that frequency parameter increases for both the mode of vibration. Similar pattern is observed on comparing table 6 and 8 in which non-homogeneity constant is 0.4. Table 9 and 10 clearly shows that frequency parameter 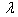 decreases with increasing value of non-homogeneity constant
decreases with increasing value of non-homogeneity constant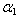 . Also when aspect ratio c/b increased from 0.5 to 1.0, frequency parameter decreases for both the mode of vibration
. Also when aspect ratio c/b increased from 0.5 to 1.0, frequency parameter decreases for both the mode of vibrationTable 1. Frequency parameter (
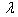 ) for a trapezoidal plate for different values of taper constant ( ) for a trapezoidal plate for different values of taper constant (
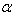 ), thermal gradient ( ), thermal gradient (
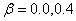 ), non-homogeneity constant ( ), non-homogeneity constant (
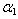 = 0.4, 1.0) and aspect ratios (a/b = 1.0), (c/b = 0.5) = 0.4, 1.0) and aspect ratios (a/b = 1.0), (c/b = 0.5)
 |
| |
|
Table 2. Frequency parameter (
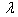 ) for a trapezoidal plate for different values of taper constant ( ) for a trapezoidal plate for different values of taper constant (
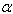 ), thermal gradient ( ), thermal gradient (
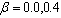 ), non-homogeneity constant ( ), non-homogeneity constant (
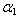 = 0.4, 1.0) and aspect ratios (a/b = 1.0), (c/b = 1.0) = 0.4, 1.0) and aspect ratios (a/b = 1.0), (c/b = 1.0)
 |
| |
|
Table 3. Frequency parameter (
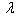 ) for a trapezoidal plate for different values of thermal gradient ) for a trapezoidal plate for different values of thermal gradient
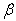 , taper constant ( , taper constant (
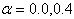 ), non-homogeneity constant ( ), non-homogeneity constant (
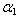 = 0.4, 1.0) and aspect ratios (a/b = 1.0), (c/b = 0.5) = 0.4, 1.0) and aspect ratios (a/b = 1.0), (c/b = 0.5)
 |
| |
|
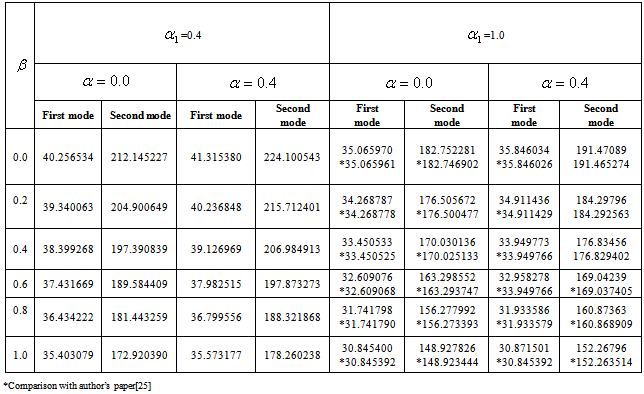
Table 4. Frequency parameter (
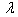 ) for a trapezoidal plate for different values of thermal gradient ) for a trapezoidal plate for different values of thermal gradient
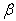 , taper constant ( , taper constant (
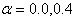 ), non-homogeneity constant ( ), non-homogeneity constant (
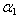 = 0.4, 1.0) and aspect ratios (a/b = 1.0), (c/b = 1.0) = 0.4, 1.0) and aspect ratios (a/b = 1.0), (c/b = 1.0)
 |
| |
|
Table 5. Frequency parameter (
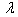 ) for a trapezoidal plate for different combinations of thermal gradient ( ) for a trapezoidal plate for different combinations of thermal gradient (
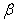 ), taper constant ( ), taper constant (
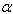 ) and fixed value of non-homogeneity constant ( ) and fixed value of non-homogeneity constant (
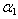 = 0.0) & aspect ratio (a/b = 0.75) = 0.0) & aspect ratio (a/b = 0.75)
 |
| |
|
Table 6. Frequency parameter (
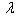 ) for a trapezoidal plate for different combinations of thermal gradient ( ) for a trapezoidal plate for different combinations of thermal gradient (
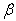 ), taper constant ( ), taper constant (
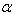 ) and fixed value of non-homogeneity constant ( ) and fixed value of non-homogeneity constant (
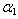 = 0.4) and aspect ratio (a/b = 0.75) = 0.4) and aspect ratio (a/b = 0.75)
 |
| |
|
Table 7. Frequency parameter (
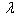 ) for a trapezoidal plate for different combinations of thermal gradient ( ) for a trapezoidal plate for different combinations of thermal gradient (
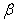 ), taper constant ( ), taper constant (
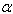 ) and fixed value of non-homogeneity constant ( ) and fixed value of non-homogeneity constant (
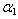 = 0.0) and aspect ratio (a/b = 1.0) = 0.0) and aspect ratio (a/b = 1.0)
 |
| |
|
Table 8. Frequency parameter (
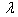 ) for a trapezoidal plate for different combinations of thermal gradient ( ) for a trapezoidal plate for different combinations of thermal gradient (
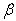 ), taper constant ( ), taper constant (
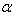 ) and fixed value of non-homogeneity constant ( ) and fixed value of non-homogeneity constant (
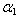 = 0.4) and aspect ratio (a/b = 1.0) = 0.4) and aspect ratio (a/b = 1.0)
 |
| |
|
Table 9. Frequency parameter (
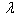 ) for a trapezoidal plate for different value of non-homogeneity constant with different combinations of thermal gradient ( ) for a trapezoidal plate for different value of non-homogeneity constant with different combinations of thermal gradient (
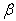 ) and taper constant ( ) and taper constant (
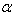 ) and aspect ratios (a/b = 1.0), (c/b = 0.5) ) and aspect ratios (a/b = 1.0), (c/b = 0.5)
 |
| |
|
Table 10. Frequency parameter (
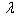 ) for a trapezoidal plate for different value of non-homogeneity constant with different combinations of thermal gradient ( ) for a trapezoidal plate for different value of non-homogeneity constant with different combinations of thermal gradient (
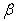 ) and taper constant ( ) and taper constant (
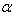 ) and aspect ratios (a/b = 1.0), (c/b = 1.0) ) and aspect ratios (a/b = 1.0), (c/b = 1.0)
 |
| |
|
5. Confirmation of Results
The accuracy of the present computations is compared with the published results[25] for C-S-C-Snon-homogeneous trapezoidal plate with non-homogeneity constant 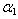 = 1.0, aspect ratio a/b = 1.0, c/b = 0.5, 1.0 and thermal gradient
= 1.0, aspect ratio a/b = 1.0, c/b = 0.5, 1.0 and thermal gradient  = 0.0 to 1.0 and taper constant
= 0.0 to 1.0 and taper constant 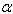 = 0.0 to 1.0. Table 1, 2, 3 and 4 shows a comparison of the values of frequency parameter obtained in the present problem and published paper of the authors[25]. A very close agreement is seen between the present results and of the published paper in which homogeneous plate with parabolically varying thickness (density is constant) has been considered.
= 0.0 to 1.0. Table 1, 2, 3 and 4 shows a comparison of the values of frequency parameter obtained in the present problem and published paper of the authors[25]. A very close agreement is seen between the present results and of the published paper in which homogeneous plate with parabolically varying thickness (density is constant) has been considered.
6. Conclusions
The main purpose of the present work is to study the effect of thermal gradient on the frequencies of C-S-C-S non-homogeneous trapezoidal plate with other plate parameters as taper constant, non-homogeneity constant and aspect ratios. Thickness of the plate varies parabolically and density varies linearly. Rayleigh-Ritz technique is used to find frequencies for first two modes of vibration. Study shows that frequency parameters increases with increasing value of taper constant and aspect ratio a/b whereas it decreases with increasing value of non-homogeneity constant, thermal gradient and aspect ratio c/b.
References
| [1] | Sharma S, Lal R, Neelam. Free transverse vibrations of non-homogeneous circular plates of linearly varying thickness. Journal of International Academy of Physical Sciences 2011; 15: 187-200. |
| [2] | Gupta AK, Panwar V, Vats RP. Vibrations of non-homogeneous rectangular plate of variable thickness in both directions with thermal gradient effect. Int. J. of Appl. Math and Mech. 2010; 6:19-37. |
| [3] | Gutierrez RH, Laura PAA. Fundamental frequency of vibrating rectangular, non-homogeneous plates. Applied Acoustics 1985; 18: 171-180. |
| [4] | Gupta AK, Kumar L. Effect of thermal gradient on free vibration of non-homogeneous visco-elastic rectangular plate of parabolically varying thickness. Acta Technica CSAV 2009; 54: 359-374. |
| [5] | Gupta AK, Agarwal N, Kaur H. Transverse vibration of non-homogeneous orthotropic visco-elastic circular plate of varying parabolic thickness. Mathematical Methods in the Applied Sciences 2011; 34: 2065-2076. |
| [6] | Lal R, Kumar Y, Gupta US. Transverse vibrations of non-homogeneous rectangular plates of uniform thickness using boundary characteristic orthogonal polynomials. Int. J. Applied Mathematics and Mechanics 2010; 6: 93-109. |
| [7] | Gupta AK, Agarwal N, Gupta DV, Kumar S, Sharma P. Effect of non-homogeneity on the free vibrations of orthotropic visco-elastic rectangular plate of parabolic varying thick-ness. Adv. Studies Theor. Phys. 2010; 4: 467-486. |
| [8] | Gupta AK, Kumar L. Thermal effect on vibration of non-homogenous visco-elastic rectang-ular plate of linear varying thickness. Meccanica 2008; 43: 47-54. |
| [9] | Gupta AK, Kumar A, Gupta DV. Vibration of visco-elastic orthotropic parallelogram plate with parabolically thickness variation. Annals of Faculty Engineering, Hunedoara, International Journal of Engineering 2012; 10: 61-70. |
| [10] | El-Sayad MA, Ghazy SSA. Rayleigh-Ritz method for free vibration of midline trapezoidal plates. Canadian Journal on Science and Engineering Mathematics 2012; 3: 159-166. |
| [11] | Gupta AK, Kumar L. Free vibration analysis of non-homogeneous visco-elastic circular plate with varying thickness subjected to thermal gradient. Acta Technica CSAV 2011; 56: 217-232. |
| [12] | Lal R, Dhanpati. Transverse vibrations of non-homogeneous orthotropic rectangular plates of variable thickness. J. Sound and Vibration 2007; 306: 203-214. |
| [13] | Gupta US, Lal R, Sharma S. Vibration analysis of non-homogeneous circular plate of nonlinear thickness variation by differential quadrature method. J. Sound and Vibration 2006; 298: 892-906. |
| [14] | Chakraverty S, Jindal R, Agarwal VK. Effect of non-homogeneity on natural frequencies of vibration of elliptic plates. Meccanica 2007; 42: 585-599. |
| [15] | Chen WQ, Lee KY, Ding HJ. On free vibration of non-homogeneous transversely isotropicmagneto-electroelastic plates. J. Sound and Vibration 2005; 279: 237-251. |
| [16] | Gupta AK, Agarwal N, Gupta DV, Kumar M. Study the non-homogeneity effect on vibration of orthotropic visco-elastic rectangular plate of linearly varying thickness. Int. Review of Pure and Applied Mathematics 2010; 6: 235-248. |
| [17] | Gupta AK, Sharma S. Study the effect of thermal gradient on transverse vibration of non-homogeneous orthotropic trapezoidal plate of parabolically varying thickness. Applied Mathematics 2011; 2: 1-10. |
| [18] | Chen CC, Kitipornchai S, Lim CW, Liew KM. Free vibration of cantilevered symmetrically laminated thick trapezoidal plates. Int. J. Mechanical Sciences 1999; 41: 685-702. |
| [19] | Bambill DV, Laura PAA, Rossi RE. Transverse vibrations of rectangular, trapezoidal and triangular orthotropic, cantilever plates. J. Sound and Vibration 1998; 210: 286-290. |
| [20] | Gupta AK, Sharma S. Thermally induced vibration of orthotropic trapezoidal plate of linearly varying thickness. J. Vibration and Control 2011; 17: 1591-1598. |
| [21] | Gurses M, Civalek O, Ersoy H. Analysis of shear deformable laminated composite trape-zoidal plates. Materials and Design 2009; 30: 3030-3035. |
| [22] | Kitipornchai S, Xiang Y, Liew KM, Lim MK. A global approach for vibration of thick trapezoidal plates. Computers and Structures 1994; 53: 83-92. |
| [23] | Gupta AK, Sharma P. Study the thermal gradient effect on frequencies of a trapezoidal plate of linearly varying thickness. Applied Mathematics 2010; 1: 356-364. |
| [24] | Gupta AK, Sharma P. Thermal effect on vibration of non-homogeneous trapezoidal plate of linearly varying thickness. Int. J. of Applied Mathematics and Mechanics 2011; 7: 1-17. |
| [25] | Gupta AK, Sharma P. Effect of linear thermal gradient on vibrations of trapezoidal plates whose thickness varies parabolically. J. Vibration and Control 2012; 18: 395-403. |


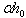 is the minimum plate thickness occurring at the right edge.
is the minimum plate thickness occurring at the right edge.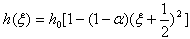
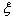 = x/a= -1/2. Non-homogeneity of plate arises due to variation in density which is linear in x direction and is of the form
= x/a= -1/2. Non-homogeneity of plate arises due to variation in density which is linear in x direction and is of the form 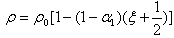


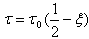
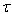 denotes the temperature excess above the reference temperature at a distance
denotes the temperature excess above the reference temperature at a distance 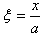 and
and 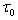 denotes the temperature excess above the reference temperature at the end
denotes the temperature excess above the reference temperature at the end 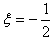 . For most of the elastic materials, modulus of elasticity is described as
. For most of the elastic materials, modulus of elasticity is described as 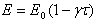
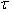 = 0 and
= 0 and 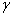 is the slope of the variation of E with
is the slope of the variation of E with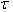 . On substituting value of
. On substituting value of 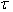 from equation (3) into (4)
from equation (3) into (4)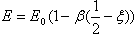
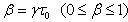 .
.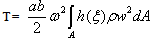
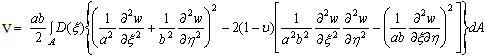
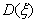 is the flexural rigidity of the plate, which is given by
is the flexural rigidity of the plate, which is given by 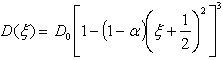
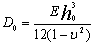
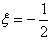 , A is the area of the plate and
, A is the area of the plate and  is the mass density per unit area of the plate.Using equation (9) and (5) in (8) flexural rigidity is given by
is the mass density per unit area of the plate.Using equation (9) and (5) in (8) flexural rigidity is given by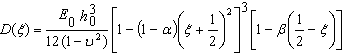
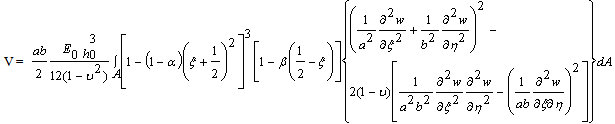
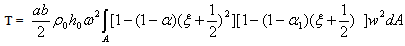
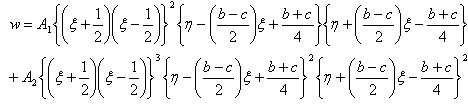

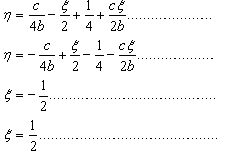
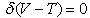
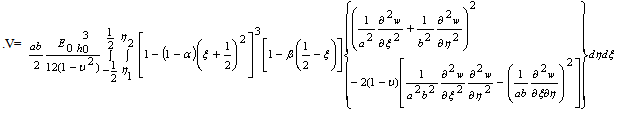
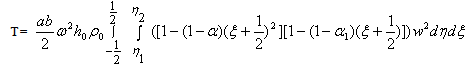
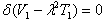

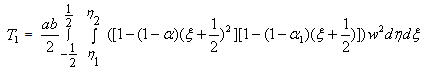
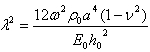 is a frequency parameter.Equation (18) involves the unknown A1 and A2 arising due to the substitution of
is a frequency parameter.Equation (18) involves the unknown A1 and A2 arising due to the substitution of 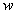 from eq (13). These two constants are to be determined from eq. (18), as follows
from eq (13). These two constants are to be determined from eq. (18), as follows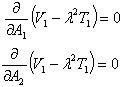
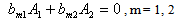
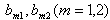 involve parametric constant and the frequency parameter.For a non-zero solution, it is desired that co-efficient of eq. (22) must be zero. So one gets the frequency equation as
involve parametric constant and the frequency parameter.For a non-zero solution, it is desired that co-efficient of eq. (22) must be zero. So one gets the frequency equation as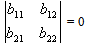
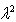 from which the two values can found which constitutes first and second mode of vibration.
from which the two values can found which constitutes first and second mode of vibration.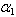 ), taper constant (
), taper constant (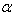 ), thermal gradient (
), thermal gradient (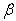 ) and aspect ratios (a/b, c/b) has been considered. All results are presented in tabular form.Table 1 and 2: These tables shows the effect of taper constant
) and aspect ratios (a/b, c/b) has been considered. All results are presented in tabular form.Table 1 and 2: These tables shows the effect of taper constant 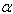 (0.0 to 1.0) on the frequency parameter
(0.0 to 1.0) on the frequency parameter 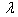 for
for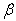 = 0.0, 0.4, = 0.4, 1.0, a/b = 1.0 and c/b = 0.5, 1.0.Table 3 and 4: These tables shows the behaviour of the frequency parameter
= 0.0, 0.4, = 0.4, 1.0, a/b = 1.0 and c/b = 0.5, 1.0.Table 3 and 4: These tables shows the behaviour of the frequency parameter 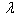 with thermal gradient
with thermal gradient 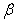 ( 0.0 to 1.0), for
( 0.0 to 1.0), for 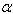 = 0.0, 0.4,
= 0.0, 0.4, 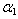 = 0.4, 1.0, a/b = 1.0 and c/b = 0.5, 1.0.Table 5, 6, 7 and 8: These tables show the effects of the frequency parameter
= 0.4, 1.0, a/b = 1.0 and c/b = 0.5, 1.0.Table 5, 6, 7 and 8: These tables show the effects of the frequency parameter 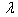 with aspect ratio c/b for different combinations of
with aspect ratio c/b for different combinations of 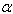 and
and 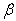 as follows.(i)
as follows.(i) 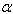 = 0.0,
= 0.0, 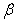 = 0.0(ii)
= 0.0(ii) 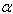 = 0.0,
= 0.0, 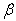 = 0.4(iii)
= 0.4(iii) 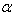 = 0.4,
= 0.4, 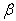 = 0.0(iv)
= 0.0(iv) 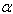 = 0.4,
= 0.4, 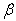 = 0.4.Non-homogeneity constant
= 0.4.Non-homogeneity constant 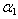 varies from 0.0 to 0.4, aspect ratio a/b varies from 0 .75 to 1.0 and aspect ratio c/b varies from 0.25 to 1.0.Table 9 and 10: In these tables effect of non-homogeneity constant (0.0 to 1.0) on frequency parameter has been shown. Four combinations of
varies from 0.0 to 0.4, aspect ratio a/b varies from 0 .75 to 1.0 and aspect ratio c/b varies from 0.25 to 1.0.Table 9 and 10: In these tables effect of non-homogeneity constant (0.0 to 1.0) on frequency parameter has been shown. Four combinations of 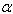 and
and 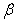 (as in table 5 to 8), two values of aspect ratio c/b (0.5, 1.0) and one value of aspect ratio a/b (1.0) has been taken. In table 1 and 2 it is observed that the frequency parameter
(as in table 5 to 8), two values of aspect ratio c/b (0.5, 1.0) and one value of aspect ratio a/b (1.0) has been taken. In table 1 and 2 it is observed that the frequency parameter 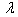 increases with increasing values of taper constant
increases with increasing values of taper constant 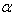 for both the modes of vibration. The rate of increase as well as the value of frequency parameter
for both the modes of vibration. The rate of increase as well as the value of frequency parameter 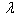 is higher in second mode in comparison to the first mode. Further on comparing the results of table 1 and 2 it is found that on increasing the value of aspect ratio c/b from 0.5 to 1.0, frequency parameter decreases for both the modes of vibration.In table 3 and 4 it is seen that frequency parameter
is higher in second mode in comparison to the first mode. Further on comparing the results of table 1 and 2 it is found that on increasing the value of aspect ratio c/b from 0.5 to 1.0, frequency parameter decreases for both the modes of vibration.In table 3 and 4 it is seen that frequency parameter 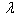 decreases with increasing values of thermal gradient
decreases with increasing values of thermal gradient 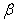 whatever be the values of other plate parameters. The rate of decrease as well as the value of frequency parameter
whatever be the values of other plate parameters. The rate of decrease as well as the value of frequency parameter 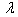 is higher in second mode in comparison to the first mode. Also on increasing aspect ratio c/b from 0.5 to 1.0, frequency parameter decreases for both the modes of vibration.It is noticed from table 5, 6, 7 and 8 that the frequency parameter
is higher in second mode in comparison to the first mode. Also on increasing aspect ratio c/b from 0.5 to 1.0, frequency parameter decreases for both the modes of vibration.It is noticed from table 5, 6, 7 and 8 that the frequency parameter 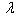 decreases with increasing values of aspect ratio c/b. Further if we compare table 5 and 6 (a/b = 0.75) it is found that the frequency parameter decreases with increase in non-homogeneity constant
decreases with increasing values of aspect ratio c/b. Further if we compare table 5 and 6 (a/b = 0.75) it is found that the frequency parameter decreases with increase in non-homogeneity constant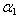 i.e. from 0.0 to 0.4. Similar pattern is observed on comparing table 7 and 8 (a/b = 1.0).Now if we compare table 5 and 7 in which aspect ratio a/b increased from 0.75 to 1.0 and non-homogeneity constant is 0.0. It is observed that frequency parameter increases for both the mode of vibration. Similar pattern is observed on comparing table 6 and 8 in which non-homogeneity constant is 0.4. Table 9 and 10 clearly shows that frequency parameter
i.e. from 0.0 to 0.4. Similar pattern is observed on comparing table 7 and 8 (a/b = 1.0).Now if we compare table 5 and 7 in which aspect ratio a/b increased from 0.75 to 1.0 and non-homogeneity constant is 0.0. It is observed that frequency parameter increases for both the mode of vibration. Similar pattern is observed on comparing table 6 and 8 in which non-homogeneity constant is 0.4. Table 9 and 10 clearly shows that frequency parameter 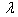 decreases with increasing value of non-homogeneity constant
decreases with increasing value of non-homogeneity constant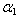 . Also when aspect ratio c/b increased from 0.5 to 1.0, frequency parameter decreases for both the mode of vibration
. Also when aspect ratio c/b increased from 0.5 to 1.0, frequency parameter decreases for both the mode of vibration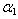 = 1.0, aspect ratio a/b = 1.0, c/b = 0.5, 1.0 and thermal gradient
= 1.0, aspect ratio a/b = 1.0, c/b = 0.5, 1.0 and thermal gradient 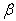 = 0.0 to 1.0 and taper constant
= 0.0 to 1.0 and taper constant 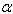 = 0.0 to 1.0. Table 1, 2, 3 and 4 shows a comparison of the values of frequency parameter obtained in the present problem and published paper of the authors[25]. A very close agreement is seen between the present results and of the published paper in which homogeneous plate with parabolically varying thickness (density is constant) has been considered.
= 0.0 to 1.0. Table 1, 2, 3 and 4 shows a comparison of the values of frequency parameter obtained in the present problem and published paper of the authors[25]. A very close agreement is seen between the present results and of the published paper in which homogeneous plate with parabolically varying thickness (density is constant) has been considered.  Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML ) for a trapezoidal plate for different values of taper constant (
) for a trapezoidal plate for different values of taper constant (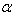 ), thermal gradient (
), thermal gradient (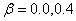 ), non-homogeneity constant (
), non-homogeneity constant (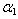 = 0.4, 1.0) and aspect ratios (a/b = 1.0), (c/b = 0.5)
= 0.4, 1.0) and aspect ratios (a/b = 1.0), (c/b = 0.5) 
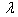 ) for a trapezoidal plate for different values of taper constant (
) for a trapezoidal plate for different values of taper constant (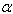 ), thermal gradient (
), thermal gradient (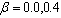 ), non-homogeneity constant (
), non-homogeneity constant (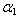 = 0.4, 1.0) and aspect ratios (a/b = 1.0), (c/b = 1.0)
= 0.4, 1.0) and aspect ratios (a/b = 1.0), (c/b = 1.0) 
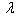 ) for a trapezoidal plate for different values of thermal gradient
) for a trapezoidal plate for different values of thermal gradient 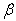 , taper constant (
, taper constant (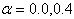 ), non-homogeneity constant (
), non-homogeneity constant (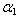 = 0.4, 1.0) and aspect ratios (a/b = 1.0), (c/b = 0.5)
= 0.4, 1.0) and aspect ratios (a/b = 1.0), (c/b = 0.5) 
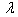 ) for a trapezoidal plate for different values of thermal gradient
) for a trapezoidal plate for different values of thermal gradient 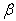 , taper constant (
, taper constant (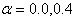 ), non-homogeneity constant (
), non-homogeneity constant (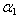 = 0.4, 1.0) and aspect ratios (a/b = 1.0), (c/b = 1.0)
= 0.4, 1.0) and aspect ratios (a/b = 1.0), (c/b = 1.0) 
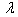 ) for a trapezoidal plate for different combinations of thermal gradient (
) for a trapezoidal plate for different combinations of thermal gradient (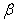 ), taper constant (
), taper constant (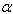 ) and fixed value of non-homogeneity constant (
) and fixed value of non-homogeneity constant (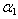 = 0.0) & aspect ratio (a/b = 0.75)
= 0.0) & aspect ratio (a/b = 0.75) 
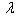 ) for a trapezoidal plate for different combinations of thermal gradient (
) for a trapezoidal plate for different combinations of thermal gradient (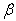 ), taper constant (
), taper constant (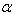 ) and fixed value of non-homogeneity constant (
) and fixed value of non-homogeneity constant (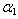 = 0.4) and aspect ratio (a/b = 0.75)
= 0.4) and aspect ratio (a/b = 0.75) 
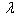 ) for a trapezoidal plate for different combinations of thermal gradient (
) for a trapezoidal plate for different combinations of thermal gradient (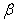 ), taper constant (
), taper constant (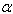 ) and fixed value of non-homogeneity constant (
) and fixed value of non-homogeneity constant (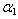 = 0.0) and aspect ratio (a/b = 1.0)
= 0.0) and aspect ratio (a/b = 1.0) 
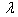 ) for a trapezoidal plate for different combinations of thermal gradient (
) for a trapezoidal plate for different combinations of thermal gradient (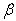 ), taper constant (
), taper constant (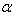 ) and fixed value of non-homogeneity constant (
) and fixed value of non-homogeneity constant (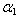 = 0.4) and aspect ratio (a/b = 1.0)
= 0.4) and aspect ratio (a/b = 1.0) 
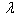 ) for a trapezoidal plate for different value of non-homogeneity constant with different combinations of thermal gradient (
) for a trapezoidal plate for different value of non-homogeneity constant with different combinations of thermal gradient (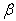 ) and taper constant (
) and taper constant (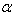 ) and aspect ratios (a/b = 1.0), (c/b = 0.5)
) and aspect ratios (a/b = 1.0), (c/b = 0.5) 
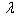 ) for a trapezoidal plate for different value of non-homogeneity constant with different combinations of thermal gradient (
) for a trapezoidal plate for different value of non-homogeneity constant with different combinations of thermal gradient (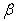 ) and taper constant (
) and taper constant (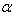 ) and aspect ratios (a/b = 1.0), (c/b = 1.0)
) and aspect ratios (a/b = 1.0), (c/b = 1.0) 