1. Introduction

Chaos is a phenomena observed in certain nonlinear dynamical systems. It is observed in a wide variety of systems such as Chua's circuit[1] in electronics, Belousov-Zhabotinsky reaction[2, 3] in chemistry, economics and finance[4-6], Rayleigh-Benard convection[7] in fluid dynamics, population dynamics[8], physiology[9, 10], pharmacodynamics[11] and meteorology[12].

E. N. Lorenz was the first to observe chaos in nonlinear system of differential equations. Lorenz system[12] represents convective motion of fluid which is cooled from above and warmed from below[13]. Few important examples of chaotic systems include Rossler system[14], Chen system[15], Liu system[16] and Lu system[17].

Chaotic trajectories are very sensitive to initial conditions i.e. the trajectories starting nearby could have completely different future. Though there is unpredictability, it is possible to make the behaviour of two (or many) nearby starting trajectories identical after some time period. This process is done by applying a suitable control and is termed as a synchronization. Examples of synchronization are abundant in nature. For the detailed discussion on this topic, readers are referred to[18-20]. Synchronization of chaotic systems have applications in secure communication[21]. Due to unpredictability, the crypto-systems based on chaotic synchronization are difficult to decode. The review on this topic is available in[22].

In this article we show that the two-scroll attractor in Bhalekar-Gejji system is formed from two one-scroll attractors. We have used a control parameter in third equation of the proposed system to study the forming procedure of the attractor.

2. Bhalekar-Gejji System

A new chaotic system[23] proposed by Bhalekar and Daftardar-Gejji is given by the system of three ordinary differential equations.

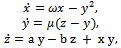(2.1)

Where , a, b are constant parameters. System (2.1) shows a chaotic behaviour for =-2.667, =10, a=27.3, b=1 as shown in Fig. 1.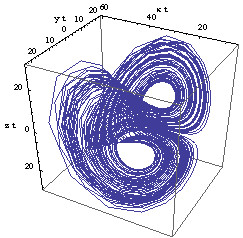

Figure 1. Chaotic phase portrait of (2.1)

Equilibrium points of the system (2.1) are given by the solutions of

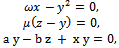(2.2)

In Table 1, equilibrium points and corresponding eigenvalues of the Jacobian matrix

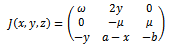are listed for the parameter values 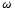=-2.667, 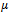=10, a=27.3, b=1.

Table 1. Equilibrium points and corresponding eigenvalues

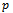An equilibrium point of the system (2.1) is called a saddle point if the Jacobian matrix at 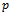has at least one eigenvalue with negative real part (stable) and one eigenvalue with non-negative real part (unstable). A saddle point is said to have index one (/two) if there is exactly one (/two) unstable eigenvalue/s. It is established in the literature[24-27] that, scrolls are generated only around the saddle points of index two. Saddle points of index one are responsible only for connecting scrolls.

3. Forming Mechanism of Attractor

In order to study the compound structure of the new attractor, we add a constant gain to the third equation.

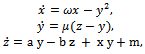(3.1)

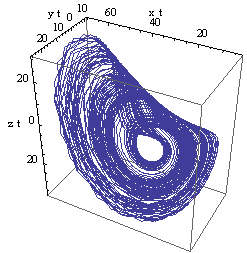Figure 2(a). Left attractor m=18.5

We get one-scroll right-attractor for m=18.5 (cf. Fig. 2(a)) whereas m=-18.5 gives the mirror image of the right-attractor i.e. the left-attractor as shown in Fig. 2(b). Thus, the new attractor is a compound structure obtained by merging together two simple one-scroll attractors.

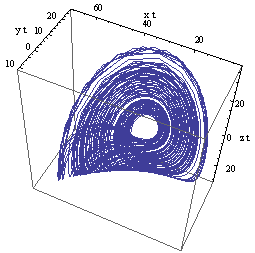Figure 2(b). Right attractor m=-18.5

Now we study the behavior of the controlled system (3.1) for different values of parameter m.

• |m|<3.2

The system is chaotic and shows double-scroll complete attractor.

• |m|<4.8

The system shows limit cycles for this range. In Fig. 3(a), the limit cycle is shown for m=3.2.

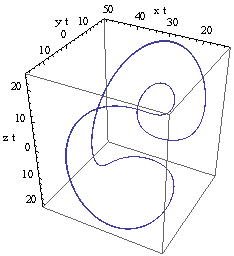Figure 3(a). Limit cycle for m=3.2

• |m|<11

The system again shows complete attractor.

• 11.1≤|m|<11.4

The periodic window is observed in this range.

• 11.4≤|m|<18.5

A partial attractor (cf. Fig. 3(b), m=14) is observed for these parameter values.

• 18.5≤|m|<18.7

Now, the system shows one-scroll (left or right) attractors.

• 18.7≤|m|<19.5

Periodic limit cycles are observed in this range of parameter.

• 19.5≤|m|<22.1

One-scroll attractors are observed in this range.

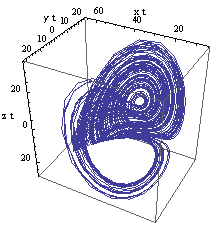Figure 3(b). Partial attractor m=14

4. Conclusions

In this article, the forming mechanism of Bhalekar-Gejji chaotic system is discussed. It is observed that the two-scroll attractor in the Bhalekar-Gejji system is formed from two one-scroll attractors. For this study, we have introduced a control parameter m in the third equation of the system. The complete double-scroll attractor observed for |m|<3.2 is transformed to a partial attractor in the range 11.4≤|m|<18.5. Limit-cycles are also observed for certain values of parameter m.