| [1] | Aki. K, and Richards. P.G : Quantitative Seismology: Theory and Methods; W.H. Freeman, San Francisco, California, 1980. |
| [2] | Ben-Menahem. A, Gillon. A : Crustal deformation by earthquakes and explosions. Bulletin of the seismological society of America.vol-60,no-1,pp193-323 215, 1971. |
| [3] | Blake.T.R, Dienes. J.K (1976) On viscosity and the inelastic nature of waves in geological media, B.S.S.A Vol-66,no-2, pp-453-465, 1976. |
| [4] | Chinnery. M.A : The deformation of the ground arround surface faults; Bull.Seis.Soc. Am,51,355-372, 1961. |
| [5] | Chinnery.M.A : The strength of the Earth's crust under horizontal shear stress; Jour.Geophysical.Res.69.2085-2089, 1964. |
| [6] | Chinnery. M.A : The vertical displacements associated with transcurrent faulting; J.Geophys.Res.70,4627-4632, 1965. |
| [7] | Chinnery.M.A and Dushan. B. Jovanovich: Effect of the earth's layering on earthquake displacement field; Bull. Seis.Soc. Am, 62, 1629-1646, 1972. |
| [8] | Cohen : Post seismic viscoelastic surface deformations and stress, 1, Theoretical considerations, Displacements and strains calculations, J.Geophys.Res. 85, No. B6, 3131-3150, 1980a. |
| [9] | Chift. P, Lin. J, Barcktiausen. U: Marine and Petroleum Geology 19,951-970, 2002. |
| [10] | Fuis. S.G, Scheirer S.D, Langenheim. E.V, Kohler. D.M : A new perspective on the geometry of the San Andreas fault of south California and iots, relationship to lithospheric structure, B.S.S.A vol-102,pp236-1251, 2012. |
| [11] | Freaund. L.B, Barnett. D.M : A two-dimensional analysis of surface deformation due to dip-slip faulting, B.S.S.A, vol-66, No-3, pp-667-675, 1976. |
| [12] | Ghosh, Mukhopadhyay. A and Sen. S: On two interacting creeping vertical surface-breaking strike-slip faults in a two-layered model of lithosphere. Physics of the Earth and planetary interior.70, 119-129, 1992. |
| [13] | Ghosh. U. and Sen. S : Stress accumulation near buried fault in lithosphere-asthenosphere system; International Journal of computing,Oct,2011,vol-I,Issue 4,pp786-795, 2011. |
| [14] | Karato. Shun-Ichiro : Rheology of the Earth's mantle: A historical review Gondwana Research-Vol.18-issue-1,pp 17-45, 2010. |
| [15] | Maruyama. T. : Statical elastic dislocations in an infinite and semi-infinite medium; Bull. Earthquake. Res. Inst., Tokyo Univ., 42, 289-368, 1964. |
| [16] | Maruyama. T. : On two dimensional dislocations in an infinite and semi-infinite medium; Bull. Earthquake Res. Inst. Tokyo Univ.,44,(part 3).p.811-871, 1966. |
| [17] | Matsu'ura. M, Sato. R : Static deformation due to fault spreading over several layers in multi-layered medium part-II-Strain and tilt; Journal of the Phys. of the Earth, vol-23,no-1,12-33, 1975. |
| [18] | Mukhopadhyay. A et al : On stress accumulation near finite rectangular fault,Indian journal of Meteorology, Hydrology and Geophysics (Mausam), vol-30, pp-347-352, 1979a. |
| [19] | Mukhopadhyay. A et al : On stress accumulation and fault slip in lithosphere, Indian journal of Meteorology, Hydrology and Geophysics (Mausam), vol-30, pp-353-358, 1979b. |
| [20] | Mukhopadhyay.A,Sen.S and Paul. B. P: On stress accumulation in a viscoelastic lithosphere containing a continuously slipping fault; Bull. Soc. Earthquake Technology,vol-17,No-1, pp-1-10, 1980,a. |
| [21] | Mukhopadhyay. A, Sen. S, and Paul. B.P : On stress accumulation near a continuously slipping fault in a two layered model of lithosphere; Bull. Soc. Earthquake Technology, vol-17, No-4,p-29-38, 1980a. |
| [22] | Matsu'ura. M, Sato. R : Static deformation due to fault spreading over several layers in multi-layered medium part-I-Strain and tilt; jour. of the phys. of the Earth, vol. 23,no-1,12-33, 1975. |
| [23] | Mansinha. L, Smylie. D.E : The Displacement fields of inclined faults; Bulletin of the seismological society of America, vol. 61, no 5, 1433-1440. 1971. |
| [24] | Nur. A, Mavko. G : Post-seismic viscoelastic rebound,Science,183,204-206, 1974. |
| [25] | Oglesby. D.D : The Dynamics of Strike-slip Step-overs with linking Dip-slip faults, B.S.S.A,vol-95, No.-5, PP-1604-1622, 2005. |
| [26] | Okada. Y : Internal deformation due to shear and tensile faults in a half-space, B.S.S.A. vol-82, No.2. pp.1018-1040, 1992. |
| [27] | Press. F : Displacements, Strains and Tilts at teleseismic Distances, Journal of Geophysical Research, vol 70, no-10, 1965. |
| [28] | Rani. S and Singh. S.J : Static deformation of a uniform half space due to a long dip-slip fault. Geophy. J. Int. vol. 109, pp 469-476, 1992. |
| [29] | Rundle. J.B: Viscoelastic crustal deformation by finite quasi-static sources, Journal of the Geophysical Research, vol-83, no-B12, pp-5937-5945, 1978. |
| [30] | Rudnicki. J.W, WU. M : Mechanics of dip-slip faulting in an elastic half-space, Journal of the Geophysical Research, vol-100, no-B11, PP-22, 173-22, 186, 1995. |
| [31] | Rybicki. K. : The elastic residual field of a very long strike slip fault in the presence of a discontinuity; Bull. Seis. Soc. Am. vol.61,79-92, 1971. |
| [32] | Sato. R. : Stress drop of finite fault; J. Phys Earth, 20, 397-407, 1972. |
| [33] | Sato. R, Yamashita. T. : Static deformations in an obliquely layered medium Part-ii dip-slip fault, Journal of the phys. of the Earth 23,113-125, 1975. |
| [34] | Savage. J.C : Displacement field for an edge dislocation in layered half space, Journal of Geophysical Research vol-103, no-B2 pp 2439-2446, 1998. |
| [35] | Savage. J.C and Hastie. L.M : Surface deformation associated with dip-slip faulting: J.G.R71,NO:20 4897-4904, 1966. |
| [36] | Segal. P. : Earthquake and volcano deformation : Princeton University Press, 2010. |
| [37] | Steketee. J.A. : On Volterra's dislocations in a semi- infinite medium; Can. J. Phys. 36. 192-205, 1958,a. |
| [38] | Steketee. J.A. : Some geophysical applications of the theory of dislocations, Can.J.Phys.36.1168-1198, 1958,b. |
| [39] | Spence. D.A and Turcotte. D.L : An elastostatic deformation of a uniform half space due to a long dip-slip fault.Geophy.j.Int.Vol.109, PP-469-476, 1976. |
| [40] | Sen. S, Sarker. S and Mukhopadhyay. A : A Creeping and surface breaking long strike -slip fault inclined to the vertical in a viscoelastic half space, Mausam, 44, 4, 365-4, 372, 1993. |
| [41] | Singh. S.J, Rosenman. M : Quasi static deformation of a viscoelastic half-space by a displacement dislocation, Phys. of the Earth and planetary interiors, 8, 87-101, 1974. |
| [42] | Singh. S.J, Punia. M, Kumari. G : Deformation of a layered half-space due to a very long dip-slip fault. Proc. Indian Natn. Sci.Acad.63A,NO-3,PP-225-240, 1997. |
| [43] | Tomar. S.K, Dhiman : 2D-Deformation analysis of a half-space due to a very long dip-slip fault at finite depth-Indian Acad. Sci.(Earth. Planet, Sci.)112, no-4, pp-587-596, 2003. |
| [44] | Yu-Ting-To, Rundle. J.B, Fernandez. J: Deformation produced by a rectangular dipping fault in a viscoelastic gravitational layered Earth model part-ii: strike-slip fault-strgrv and strgrh fortran programs, Computers and Geo Sciences vol=22,no-7, pp-751-764, 1996. |
| [45] | Zhang. C, Oglesby. D.D, Xu. G: Earthquake nucleation on dip-slip faults with depth-dependent frictional properties, Journal of Geophysical Research, vol-111, no-10, B07303, 2006. |

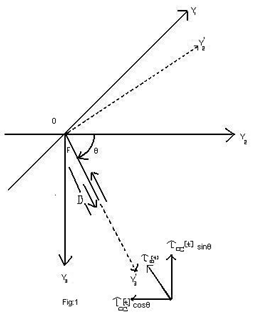

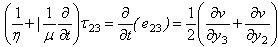

 is the effective rigidity of the material.The stresses satisfy the following equations: (assuming quasistatic deformation for which the inertia terms are neglected).
is the effective rigidity of the material.The stresses satisfy the following equations: (assuming quasistatic deformation for which the inertia terms are neglected).

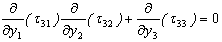
 as
as 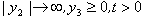


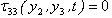
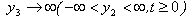
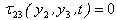
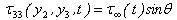
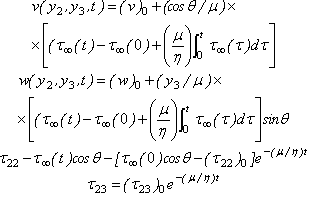
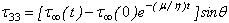
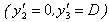 If g(x′3) be the creep function, it should satisfy the above conditions.
If g(x′3) be the creep function, it should satisfy the above conditions.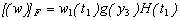 Where, H (t1) is the Heaviside function and[(w)]F = the discontinuity of w across F given by:
Where, H (t1) is the Heaviside function and[(w)]F = the discontinuity of w across F given by: We solve the resulting boundary value problem by modified Green’s function method following[16],[31] and correspondence principle (As shown in the Appendix 2) and get the solution for displacements, stresses and strain as
We solve the resulting boundary value problem by modified Green’s function method following[16],[31] and correspondence principle (As shown in the Appendix 2) and get the solution for displacements, stresses and strain as  Where,
Where,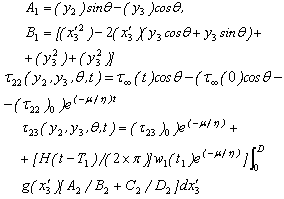 Where,
Where,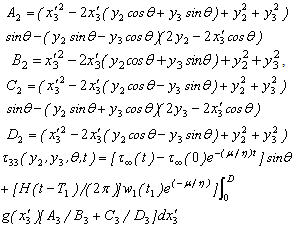 Where,
Where,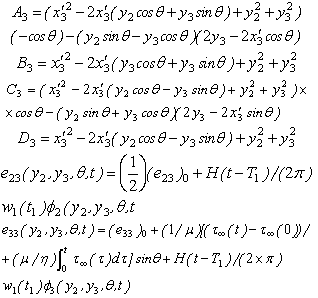 Where,
Where,  are given in Appendix 2. (B)
are given in Appendix 2. (B)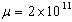 Dynes/cm2
Dynes/cm2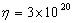 PoiseD = Depth of the fault = 10 km.,[nothing that the depth of all major earthquake faults are in between 10-15 km].
PoiseD = Depth of the fault = 10 km.,[nothing that the depth of all major earthquake faults are in between 10-15 km].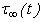 = constant =
= constant = 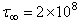 dynes/cm2 (200 bars),[post seismic observations reveal that in most of the cases, stress released in major earthquake are of the order of 200 bars or less, in extreme cases, it may be 400 bars.]
dynes/cm2 (200 bars),[post seismic observations reveal that in most of the cases, stress released in major earthquake are of the order of 200 bars or less, in extreme cases, it may be 400 bars.] Dyne/cm2 (50 bars)and
Dyne/cm2 (50 bars)and 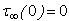 We take the creep function
We take the creep function 
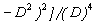 , with W = 1 cm/year, satisfying the conditions stated in
, with W = 1 cm/year, satisfying the conditions stated in  .We now compute the following quantities:
.We now compute the following quantities: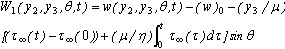

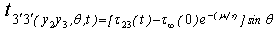
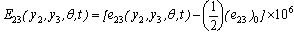

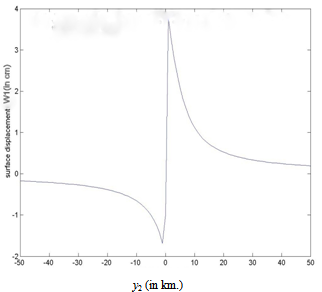
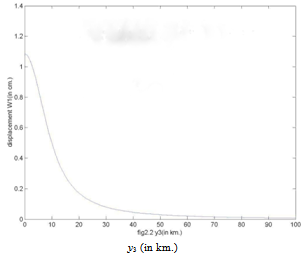
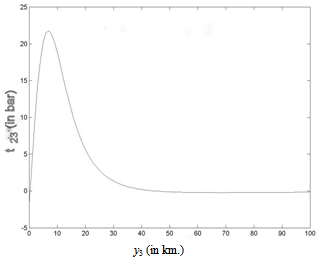
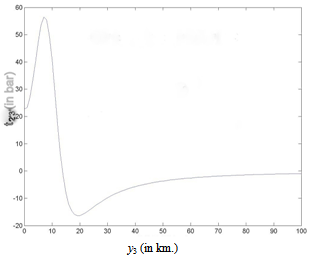
 due to the movement across the fault for different dip angle θ and at different time after the fault movement. We take t=1 year. In Figure 2 the graph shows the nature of surface displacement W1 against y2, the distance from the strike of the fault with θ=45 (in deg). It is observed that the displacement are in opposite directions across the strike of the fault. Their magnitudes gradually decrease and tend to zero as we move away from the fault. This is quite expected as the effect of the fault movement gradually die out with distance. The sudden changes of W1 near y2 = 0 is due to the dip-slip motion along the fault. This is in good conformity with the results shown in[36]. Figure 3 shows the variation of W1 with depth y3 along the vertical through a point y2 = 5 km for a vertical fault with θ=90(in deg). It shows that W1 decreases sharply upto a depth of about 15 km and thereafter diminishes to zero at a slower rate, and becomes significantly small for y3 > 100km.(B) Variation with depth of the main driving stress t2′3′ in the dip-slip direction due to the movement across F.Figures (4) – (7) show the variation of t2′3′ with depth y3 for various θ and some specific values of y2.In Figure 4, it is found that for a vertical dip-slip fault θ=90 (in degree) and at a point very near to the fault y2=1 km, t2′3′ undergoes a change (in one year) by an amount < 0.5 bar, due to the creeping movement across F. Initially there is a very small region of stress release just below the free surface (0<y3<1 km). Thereafter, the stress-accumulation region start, a maximum accumulation occurs at a depth of about 2 km below the free surface. This additional stress falls off quickly and becomes negligibly small at a depth of 20-25 km.In case of the same vertical dip slip fault but a little bit away from the fault, (y2=5 km), the characteristic of the nature of stress accumulation and release is the similar but of magnitude of much lower order (0:04bar). Figure 6 shows the variation of main driving stress component t2′3′ with the depth for y2 = 5 km, t = 1 year due to the creep movement across the fault at a dip angle θ=60(degree). The graph shows that there is a negligibly small region (<0.1 km) of stress release and then it accumulates upto a depth > 9 km and attains its maximum value 22.5 bar (approx.) for t=1 year and then decreases to 0 at a depth about 100 km.
due to the movement across the fault for different dip angle θ and at different time after the fault movement. We take t=1 year. In Figure 2 the graph shows the nature of surface displacement W1 against y2, the distance from the strike of the fault with θ=45 (in deg). It is observed that the displacement are in opposite directions across the strike of the fault. Their magnitudes gradually decrease and tend to zero as we move away from the fault. This is quite expected as the effect of the fault movement gradually die out with distance. The sudden changes of W1 near y2 = 0 is due to the dip-slip motion along the fault. This is in good conformity with the results shown in[36]. Figure 3 shows the variation of W1 with depth y3 along the vertical through a point y2 = 5 km for a vertical fault with θ=90(in deg). It shows that W1 decreases sharply upto a depth of about 15 km and thereafter diminishes to zero at a slower rate, and becomes significantly small for y3 > 100km.(B) Variation with depth of the main driving stress t2′3′ in the dip-slip direction due to the movement across F.Figures (4) – (7) show the variation of t2′3′ with depth y3 for various θ and some specific values of y2.In Figure 4, it is found that for a vertical dip-slip fault θ=90 (in degree) and at a point very near to the fault y2=1 km, t2′3′ undergoes a change (in one year) by an amount < 0.5 bar, due to the creeping movement across F. Initially there is a very small region of stress release just below the free surface (0<y3<1 km). Thereafter, the stress-accumulation region start, a maximum accumulation occurs at a depth of about 2 km below the free surface. This additional stress falls off quickly and becomes negligibly small at a depth of 20-25 km.In case of the same vertical dip slip fault but a little bit away from the fault, (y2=5 km), the characteristic of the nature of stress accumulation and release is the similar but of magnitude of much lower order (0:04bar). Figure 6 shows the variation of main driving stress component t2′3′ with the depth for y2 = 5 km, t = 1 year due to the creep movement across the fault at a dip angle θ=60(degree). The graph shows that there is a negligibly small region (<0.1 km) of stress release and then it accumulates upto a depth > 9 km and attains its maximum value 22.5 bar (approx.) for t=1 year and then decreases to 0 at a depth about 100 km. 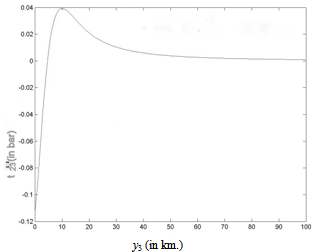
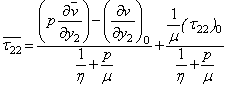
 , Laplace trans-formation variable) and similar other equations. Also the stress equations of motions in Laplace transform domain as:
, Laplace trans-formation variable) and similar other equations. Also the stress equations of motions in Laplace transform domain as: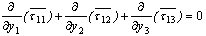
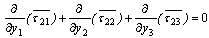
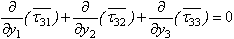


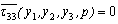
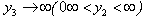
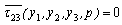
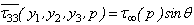
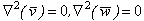
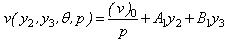

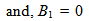
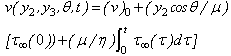
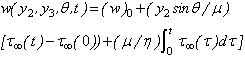
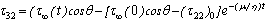
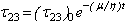


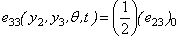
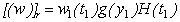


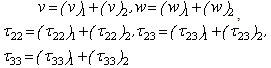
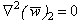
 is the Laplace transformation of (w)2, with the modified boundary condition,
is the Laplace transformation of (w)2, with the modified boundary condition,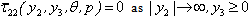

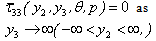


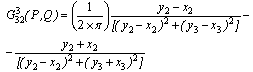
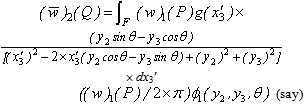
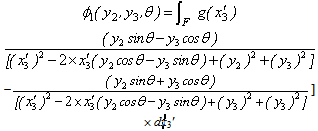
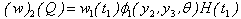 Where, H (t1) is the Heaviside step function, which gives the displacement at any points Q(y2,y3).We also have,
Where, H (t1) is the Heaviside step function, which gives the displacement at any points Q(y2,y3).We also have, where,
where, 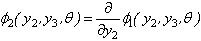
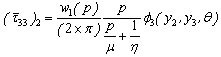 where,
where, 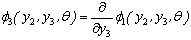
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML