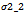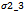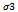-
Paper Information
- Next Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Computational and Applied Mathematics
p-ISSN: 2165-8935 e-ISSN: 2165-8943
2012; 2(6): 241-248
doi: 10.5923/j.ajcam.20120206.01
The Arithmetic Mean Solver in Lagged Diffusivity Method for Nonlinear Diffusion Equations
Emanuele Galligani
Department of Mathematics "G. Vitali", University of Modena and Reggio Emilia, Via Campi 213/b, I-41125, Modena, Italy
Correspondence to: Emanuele Galligani, Department of Mathematics "G. Vitali", University of Modena and Reggio Emilia, Via Campi 213/b, I-41125, Modena, Italy.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
This paper deals with the solution of nonlinear system arising from finite difference discretization of nonlinear diffusion convection equations by the lagged diffusivity functional iteration method combined with different inner iterative solvers. The analysis of the whole procedure with the splitting methods of the Arithmetic Mean (AM) and of the Alternating Group Explicit (AGE) has been developed. A comparison in terms of number of iterations has been done with the BiCG-STAB algorithm. Some numerical experiments have been carried out and they seem to show the effectiveness of the lagged diffusivity procedure with the Arithmetic Mean method as inner solver.
Keywords: Lagged Diffusivity, Arithmetic Mean Method, Nonlinear Finite Difference Systems
Cite this paper: Emanuele Galligani, "The Arithmetic Mean Solver in Lagged Diffusivity Method for Nonlinear Diffusion Equations", American Journal of Computational and Applied Mathematics, Vol. 2 No. 6, 2012, pp. 241-248. doi: 10.5923/j.ajcam.20120206.01.
Article Outline
1. Introduction
- We consider a nonlinear diffusion convection equation where the diffusion coefficient, denoted by σ, depends on the solution.When we use a finite difference discretization, this elliptic equation supplemented by a suitable boundary condition, can be transcribed into a nonlinear system of algebraic equations.We wish to compute a solution of this system of nonlinear equations with a common iterative procedure in which the nonlinear term, corresponding to the discretization of the diffusivity σ, may be evaluated at the previous iteration (see[22]). In literature, this approach of nonlinearity lagging in the diffusivity term is denoted as Lagged Diffusivity Fixed Point Iteration or Lagged Diffusivity Functional Iteration.In Section 2, a model problem described by a nonlinear diffusion convection equation subject to homogeneous Dirichlet boundary conditions is presented and a finite difference discretization is described. Then, the lagged diffusivity procedure for the solution of this nonlinear difference system is stated.Since, a purpose here is to re-examine the lagged diffusivity procedure for solving the system of nonlinear difference equations of elliptic type in the context of Parallel Computing, the linear difference system that arises at each iteration of the lagged diffusivity procedure is solved with the iterative splitting methods of the Arithmetic Mean introduced in[20-21] and of the Alternating Group Explicit (AGE) introduced by Evans (see[1-3]).Thus, the outer iterates of the lagged diffusivity procedure are the approximate solutions of the linear systems computed with an inner iterative solver; a criterion for acceptability of these approximate solutions is given. A stopping rule for the lagged diffusivity procedure is also given.Section 3 is devoted to remind the Arithmetic Mean method and AGE method for the solution of linear systems with block tridiagonal coefficient matrix.In Section 4, the convergence of the lagged diffusivity iteration method is analysed under mild and reasonable assumptions imposed on the diffusivity σ using well known standard techniques (see[16]).In Section 5, numerical experiments show the behaviour of the inner-outer iterations of the procedure. In this section a comparison of the lagged diffusivity iteration method with different iterative solvers is also presented. The Arithmetic Mean and the AGE methods are compared, in terms of number of iterations, with BiCG-STAB method (see[23]).
2. The Lagged Diffusivity Functional Iteration Method
- Consider the model problem described by the nonlinear diffusion convection equation
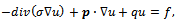 | (1) |
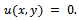 | (2) |
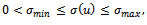 uniformly in u; in addition, q(x,y) ≥ qmin ≥ 0;(iii) for fixed (x,y)∈R, the function σ(u) satisfies Lipschitz condition in u with constant Γ (uniformly in x, y), Γ > 0.The nonlinearity introduced by the u-dependence of the coefficient σ(u) requires that, in general, the solution of equation (1) is approximated by numerical methods.We superimpose on R∪∂R a grid of points Rh∪∂Rh; the set of the internal points Rh of the grid are the mesh points
uniformly in u; in addition, q(x,y) ≥ qmin ≥ 0;(iii) for fixed (x,y)∈R, the function σ(u) satisfies Lipschitz condition in u with constant Γ (uniformly in x, y), Γ > 0.The nonlinearity introduced by the u-dependence of the coefficient σ(u) requires that, in general, the solution of equation (1) is approximated by numerical methods.We superimpose on R∪∂R a grid of points Rh∪∂Rh; the set of the internal points Rh of the grid are the mesh points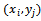 , for i = 1, ..., N and j = 1, ..., M, with uniform mesh size h along x and y directions respectively, i.e.
, for i = 1, ..., N and j = 1, ..., M, with uniform mesh size h along x and y directions respectively, i.e. 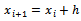 and
and 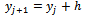 for i = 0, ..., N, j = 0, ..., M.Thus, at the mesh points of R∪∂R,
for i = 0, ..., N, j = 0, ..., M.Thus, at the mesh points of R∪∂R, 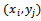 for i = 0, ..., N+1, j = 0, ..., M+1, the solution
for i = 0, ..., N+1, j = 0, ..., M+1, the solution 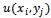 is approximated by a grid function
is approximated by a grid function 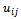 defined on Rh∪∂Rh and satisfying the boundary condition (2) on ∂Rh.In order to approximate partial derivatives in (1) we shall make use of difference quotients of grid functions. The forward, backward and centered difference quotients with respect to x and to y of the grid function
defined on Rh∪∂Rh and satisfying the boundary condition (2) on ∂Rh.In order to approximate partial derivatives in (1) we shall make use of difference quotients of grid functions. The forward, backward and centered difference quotients with respect to x and to y of the grid function 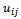 at the mesh point
at the mesh point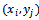 , are, respectively:
, are, respectively: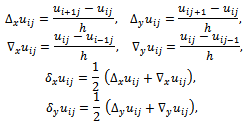 while the centered second difference quotient with respect to x and to y can be written
while the centered second difference quotient with respect to x and to y can be written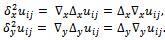 This notation was introduced by Courant et al. in[4].Providing a discretization error O(h2), the finite difference approximation of (1) in
This notation was introduced by Courant et al. in[4].Providing a discretization error O(h2), the finite difference approximation of (1) in 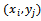 , i = 1, ..., N, j = 1, ..., M, is given by
, i = 1, ..., N, j = 1, ..., M, is given by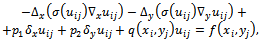 | (3) |
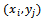 , (i.e., l=(j-1)•N+i with j = 1, ..., M, and i = 1, ..., N), we can write the vector u of components
, (i.e., l=(j-1)•N+i with j = 1, ..., M, and i = 1, ..., N), we can write the vector u of components 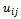 and the difference equations (3) as the nonlinear system
and the difference equations (3) as the nonlinear system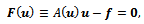 | (4) |
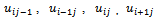 respectively, are
respectively, are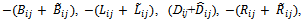 , and
, and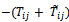 , where
, where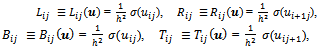 | (5) |
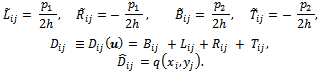 | (6) |
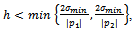 | (7) |
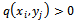 ) or irreducibly (when
) or irreducibly (when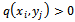 ) diagonally dominant ([24, p. 23]) and has positive diagonal elements,
) diagonally dominant ([24, p. 23]) and has positive diagonal elements, 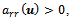 r = 1, ..., n, and nonpositive off diagonal elements
r = 1, ..., n, and nonpositive off diagonal elements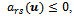
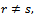 with r,s = 1, ..., n; therefore A(u) is an
with r,s = 1, ..., n; therefore A(u) is an 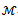 -matrix ([24, p. 91] or[18, p. 110]).In the case of diffusion equation
-matrix ([24, p. 91] or[18, p. 110]).In the case of diffusion equation 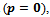 , the matrix A(u) is also symmetric; then it is a symmetric and positive definite matrix ([24, p. 91]).The vector f in (4) has components
, the matrix A(u) is also symmetric; then it is a symmetric and positive definite matrix ([24, p. 91]).The vector f in (4) has components 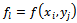 for i = 1, ..., N, j = 1, ..., M and l = (j-1) • N+i.We remark that while the grid function
for i = 1, ..., N, j = 1, ..., M and l = (j-1) • N+i.We remark that while the grid function 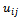 is defined on the whole mesh region Rh∪∂Rh, the vector
is defined on the whole mesh region Rh∪∂Rh, the vector 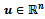 represents the grid function
represents the grid function 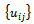 defined only on the interior mesh points Rh.Here, we suppose that a solution
defined only on the interior mesh points Rh.Here, we suppose that a solution 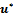 of the system (4) exists in
of the system (4) exists in 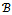 (see Section 4).For solving the nonlinear system (4) the easiest and maybe the most common method is to lag the nonlinear term in (4) generating an iterative procedure denoted as Lagged Diffusivity Functional Iteration.With this iterative procedure the nonlinear system (4) can be solved via a sequence of systems of linear equations.Specifically, given a sequence of positive numbers
(see Section 4).For solving the nonlinear system (4) the easiest and maybe the most common method is to lag the nonlinear term in (4) generating an iterative procedure denoted as Lagged Diffusivity Functional Iteration.With this iterative procedure the nonlinear system (4) can be solved via a sequence of systems of linear equations.Specifically, given a sequence of positive numbers 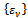 such that
such that  as
as 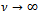 and an initial estimate
and an initial estimate 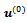 of the solution
of the solution 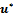 of the system (4), we generate a sequence of iterates
of the system (4), we generate a sequence of iterates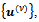
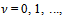 with the following rule for the transition from a current iteration
with the following rule for the transition from a current iteration 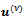 to the new iterate
to the new iterate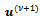 :● Find an approximate solution
:● Find an approximate solution 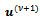 of the linear system
of the linear system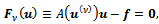 | (8) |
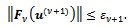 | (9) |
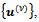 and by an inner iterative solver of the linear system (8). This solver must be particularly well suited for implementation on parallel computers.The termination criterion for the outer iteration is provided by the following stopping rule
and by an inner iterative solver of the linear system (8). This solver must be particularly well suited for implementation on parallel computers.The termination criterion for the outer iteration is provided by the following stopping rule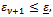 | (10) |
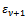 decreases as
decreases as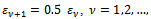 , with
, with 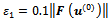 and
and 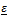 is a prespecified threshold.
is a prespecified threshold.3. Iterative Parallel Solution of the Linear Systems
- In this section, we remind the block form of the Alternating Group Explicit (AGE) and of the Arithmetic Mean methods for the solution of the linear system
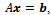 | (11) |
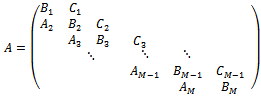 | (12) |
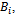 i = 1, ..., M, is a nonsingular NN matrix and the blocks
i = 1, ..., M, is a nonsingular NN matrix and the blocks 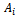 and
and 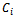 (i = 1, ..., M;
(i = 1, ..., M; 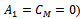 are square matrices of order N (n = N M).The AGE method consists in considering the following splitting of the matrix A
are square matrices of order N (n = N M).The AGE method consists in considering the following splitting of the matrix A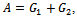 where
where 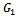 and
and 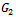 are the following matrices
are the following matrices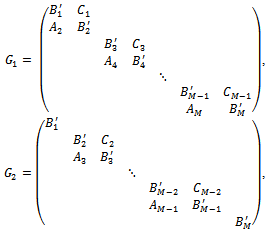 with
with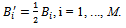 Thus, starting from a vector
Thus, starting from a vector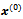 , the AGE method generates a sequence of iterates
, the AGE method generates a sequence of iterates 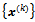 as follows; for
as follows; for 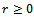 and k = 0, 1, ..., until convergence:
and k = 0, 1, ..., until convergence: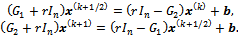 | (13) |
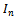 is the identity matrix of order n. The AGE method is convergent when the matrices
is the identity matrix of order n. The AGE method is convergent when the matrices 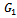 and
and 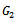 are symmetric and positive definite with
are symmetric and positive definite with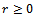 . In this case it is proved that the optimal choice for r is
. In this case it is proved that the optimal choice for r is 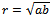 where
where and
and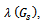 , s = 1, 2, are the eigenvalues of the matrix
, s = 1, 2, are the eigenvalues of the matrix 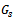 (see, e.g.[1]).Furthermore, if the matrix A is irreducibly (or strictly) diagonally dominant with positive diagonal elements,
(see, e.g.[1]).Furthermore, if the matrix A is irreducibly (or strictly) diagonally dominant with positive diagonal elements, 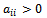 , and nonpositive off diagonal elements
, and nonpositive off diagonal elements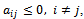 , and
, and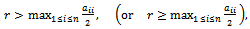 | (14) |
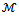 -matrix. Set
-matrix. Set 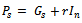 and
and 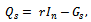 s = 1, 2. The choice of r in (14) yields that the matrices
s = 1, 2. The choice of r in (14) yields that the matrices 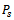 are strictly (or irreducibly) diagonally dominant and have positive diagonal elements and nonpositive off diagonal elements, then
are strictly (or irreducibly) diagonally dominant and have positive diagonal elements and nonpositive off diagonal elements, then 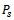 are
are 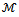 -matrices with
-matrices with 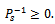 From the hypotheses on the matrix A, the matrices
From the hypotheses on the matrix A, the matrices 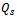 are nonnegative
are nonnegative 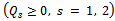 Thus, the iteration matrix T of the AGE method is
Thus, the iteration matrix T of the AGE method is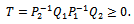 Set
Set 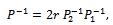 | (15) |
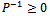 (P is an
(P is an 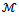 -matrix) and
-matrix) and 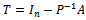 holds. Indeed, set
holds. Indeed, set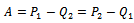 , a multiplicative splitting method can be written
, a multiplicative splitting method can be written Then,
Then,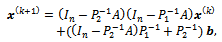 can be seen as a splitting method
can be seen as a splitting method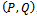 , i.e.,
, i.e., 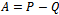 , by setting
, by setting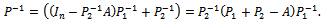 Since
Since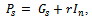 , s = 1, 2, and
, s = 1, 2, and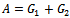 , then we have the expression (15) for
, then we have the expression (15) for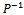 .Now, the proof runs as that of the Regular Splitting Theorem in[18, p. 119].The Arithmetic Mean method uses the following two splittings of the matrix A
.Now, the proof runs as that of the Regular Splitting Theorem in[18, p. 119].The Arithmetic Mean method uses the following two splittings of the matrix A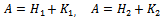 ,where
,where 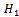 and
and 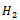 are the following matrices
are the following matrices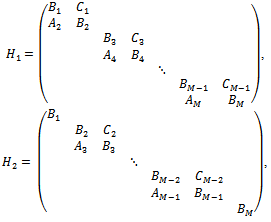 and
and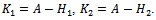 We suppose M even. If M is odd, we can proceed in a similar way.Thus, starting from a vector
We suppose M even. If M is odd, we can proceed in a similar way.Thus, starting from a vector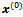 , the method of the Arithmetic Mean generates a sequence of iterates
, the method of the Arithmetic Mean generates a sequence of iterates 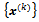 as follows; for
as follows; for 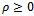 and k = 0, 1, ..., until convergence:
and k = 0, 1, ..., until convergence: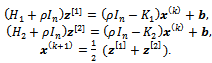 | (16) |
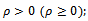 ● positive definite but not symmetric with
● positive definite but not symmetric with  where
where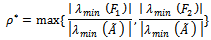 Here
Here 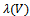 denotes an eigenvalue of a matrix V and
denotes an eigenvalue of a matrix V and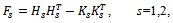 and
and 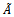 is the symmetric positive definite matrix
is the symmetric positive definite matrix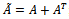 ;● symmetric positive definite with
;● symmetric positive definite with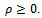 At each iteration k of the AGE method, we have to solve M /2 linear systems of order 2N, i = 1, 3, 5, ..., M -1,
At each iteration k of the AGE method, we have to solve M /2 linear systems of order 2N, i = 1, 3, 5, ..., M -1,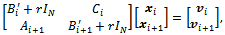 | (17) |
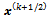 . The solution of (17) can be seen as a block partitioned vector
. The solution of (17) can be seen as a block partitioned vector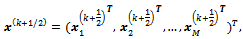 where each block has N components.Here
where each block has N components.Here 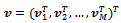 is the right hand side (r.h.s.) of the first equation of (13).These M / 2 systems can be solved simultaneously (in parallel).Then, in order to obtain the new iterate
is the right hand side (r.h.s.) of the first equation of (13).These M / 2 systems can be solved simultaneously (in parallel).Then, in order to obtain the new iterate 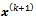 of the AGE method, we have to solve, in parallel, M / 2-1 systems as (17) with i = 2,4, 6, ..., M -2 and two linear systems of order N
of the AGE method, we have to solve, in parallel, M / 2-1 systems as (17) with i = 2,4, 6, ..., M -2 and two linear systems of order N 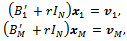 that can be solved in parallel, as well. The AGE method has an intrinsic parallelism.In the case of the additive splitting method of the Arithmetic Mean, at each iteration k we have to solve M-1 linear systems of order 2N, i = 1, 2, 3, ..., M -1,
that can be solved in parallel, as well. The AGE method has an intrinsic parallelism.In the case of the additive splitting method of the Arithmetic Mean, at each iteration k we have to solve M-1 linear systems of order 2N, i = 1, 2, 3, ..., M -1, 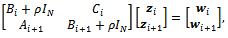 | (18) |
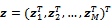 and
and 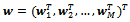 indicate the vector
indicate the vector 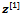 (for i = 1, 3, 5, ..., M -1) and the corresponding r.h.s. of the first equation of (16) or the vector
(for i = 1, 3, 5, ..., M -1) and the corresponding r.h.s. of the first equation of (16) or the vector 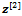 (for i = 2, 4, 6, ..., M -2) and the corresponding r.h.s. of the second equation of (16).Furthermore, we have to solve two linear systems of order N
(for i = 2, 4, 6, ..., M -2) and the corresponding r.h.s. of the second equation of (16).Furthermore, we have to solve two linear systems of order N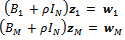 where
where 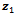 and
and 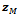 indicate the first and the last block of the vector
indicate the first and the last block of the vector 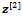 and
and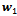 ,
, 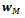 the corresponding r.h.s. of the second equation of (16).These systems can be solved in parallel. The Arithmetic Mean method introduces also an explicit parallelism in order to increase the degree of multiprogramming, that is the number of processes that can be executed simultaneously ([13, p. 87]).When the system (11) arises from the finite difference discretization of the problem (1)-(2), the diagonal blocks of A in (12) are tridiagonal while the sub and superdiagonal blocks are diagonal.Thus, the systems (17) and (18) can be solved directly as in[9, 8] or iteratively, generating a two-stage iterative method as in[12]. A direct solution of these systems can be performed by cyclic reduction solvers ([17, p. 125],[15]) combined with an approximate Schur complement method ([17, p.123, p. 217]) or with block Gaussian elimination.
the corresponding r.h.s. of the second equation of (16).These systems can be solved in parallel. The Arithmetic Mean method introduces also an explicit parallelism in order to increase the degree of multiprogramming, that is the number of processes that can be executed simultaneously ([13, p. 87]).When the system (11) arises from the finite difference discretization of the problem (1)-(2), the diagonal blocks of A in (12) are tridiagonal while the sub and superdiagonal blocks are diagonal.Thus, the systems (17) and (18) can be solved directly as in[9, 8] or iteratively, generating a two-stage iterative method as in[12]. A direct solution of these systems can be performed by cyclic reduction solvers ([17, p. 125],[15]) combined with an approximate Schur complement method ([17, p.123, p. 217]) or with block Gaussian elimination.4. Analysis of the Convergence of the Lagged Diffusivity Functional Iteration Method
- In this section, we prove the convergence of the sequence
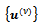 generated by the lagged diffusivity iteration method for the solution of the system (4) under the smoothness assumptions (i)-(iii).We define
generated by the lagged diffusivity iteration method for the solution of the system (4) under the smoothness assumptions (i)-(iii).We define 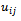 and
and 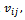 i = 0, ..., N +1 and j = 0, ..., M +1, the grid functions defined on Rh∪∂Rh and satisfying the Dirichlet boundary condition on ∂Rh. For grid functions
i = 0, ..., N +1 and j = 0, ..., M +1, the grid functions defined on Rh∪∂Rh and satisfying the Dirichlet boundary condition on ∂Rh. For grid functions 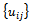 and
and 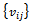 of this type, the discrete
of this type, the discrete 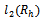 inner product and norm are defined by the formulas
inner product and norm are defined by the formulas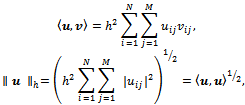 respectively.We say that the grid functions
respectively.We say that the grid functions 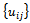 defined on Rh∪∂Rh and vanishing on ∂Rh satisfy Property A if they are uniformly bounded and have uniformly bounded backward difference quotients
defined on Rh∪∂Rh and vanishing on ∂Rh satisfy Property A if they are uniformly bounded and have uniformly bounded backward difference quotients 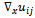 and
and 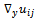 at each mesh point
at each mesh point 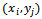 of Rh∪∂Rh. The set of all grid functions which satisfy Property A is denoted by
of Rh∪∂Rh. The set of all grid functions which satisfy Property A is denoted by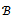 . Thus,
. Thus, 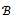 is the set of all grid functions
is the set of all grid functions 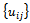 for which there exist two positive constants
for which there exist two positive constants 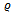 and such that
and such that 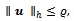 | (19) |
 | (20) |
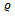 is independent of h; also
is independent of h; also 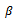 is independent of h but it depends on
is independent of h but it depends on 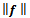 .(see[16]).We assume that the system (4),
.(see[16]).We assume that the system (4), 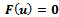 , where
, where , has at least one solution
, has at least one solution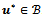 .Suppose that the system (4) arises from the discretization of problem (1)-(2) subject to the conditions (i)-(iii) with
.Suppose that the system (4) arises from the discretization of problem (1)-(2) subject to the conditions (i)-(iii) with 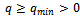 and
and 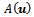 being an irreducible nonsingular
being an irreducible nonsingular 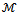 -matrix. If
-matrix. If 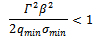 for any
for any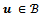 , then the mapping
, then the mapping 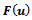 is uniformly monotone in
is uniformly monotone in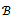 . (See[16],[5] for a proof of this result and e.g.,[19, p. 141] for the definition of uniform monotonicity). The iterate
. (See[16],[5] for a proof of this result and e.g.,[19, p. 141] for the definition of uniform monotonicity). The iterate 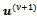 of the lagged diffusivity functional iteration method satisfies the system (8) with the acceptability criterion (9), that is
of the lagged diffusivity functional iteration method satisfies the system (8) with the acceptability criterion (9), that is 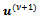 is the solution of the linear diffusion convection equation whose diffusivity depends on the previous iterate
is the solution of the linear diffusion convection equation whose diffusivity depends on the previous iterate 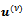 with inhomogeneous term
with inhomogeneous term 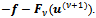 We assume that all the iterates
We assume that all the iterates 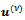 satisfy Property A. Thus in particular, by inequality (20), the backward difference quotients of each grid function are bounded and they depend on the inhomogeneous term; then, we have that there exist two constants
satisfy Property A. Thus in particular, by inequality (20), the backward difference quotients of each grid function are bounded and they depend on the inhomogeneous term; then, we have that there exist two constants 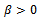 and
and 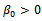 such that
such that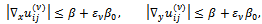 | (21) |
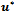 be a solution of the nonlinear system (4) with
be a solution of the nonlinear system (4) with 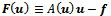 arising from the finite difference discretization of problem (1)-(2) subject to the conditions (i)-(iii) with
arising from the finite difference discretization of problem (1)-(2) subject to the conditions (i)-(iii) with 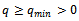 and
and 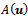 being an irreducible nonsingular
being an irreducible nonsingular 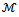 -matrix. Assume that the mapping
-matrix. Assume that the mapping 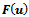 is uniformly monotone in
is uniformly monotone in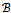 .Suppose that
.Suppose that 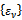 is a sequence of positive numbers such that
is a sequence of positive numbers such that 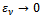 as
as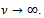 Let
Let 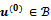 be arbitrary and let
be arbitrary and let 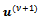 be the solution of
be the solution of 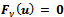 satisfying the condition (9) with
satisfying the condition (9) with 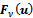 as in (8).If all the vectors
as in (8).If all the vectors 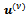 belong to
belong to 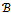 and satisfy Property A with (21) instead of (20), then the sequence
and satisfy Property A with (21) instead of (20), then the sequence 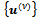 converges to
converges to 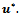 Proof. The proof runs as that in[6, Theor. 1] or in[5, Theor. 1, p. 33]. A more general result on the convergence of the lagged diffusivity functional iteration method can be obtained by defining the mapping u=G(u) where
Proof. The proof runs as that in[6, Theor. 1] or in[5, Theor. 1, p. 33]. A more general result on the convergence of the lagged diffusivity functional iteration method can be obtained by defining the mapping u=G(u) where 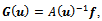 for all
for all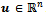 . A solution of the system (4) is a fixed point of the mapping
. A solution of the system (4) is a fixed point of the mapping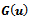 . Since the smoothness condition (iii) on
. Since the smoothness condition (iii) on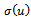 , we can have that the matrix A(u) satisfies the Lipschitz-continuity condition for every bounded subset
, we can have that the matrix A(u) satisfies the Lipschitz-continuity condition for every bounded subset 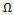 of
of 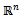 with a Lipschitz constant
with a Lipschitz constant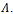 Then we can write,
Then we can write,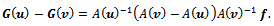 Thus, we have for
Thus, we have for 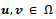
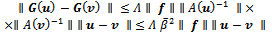 where
where 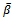 is a bound for
is a bound for 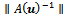 for any
for any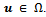 . Here,
. Here,  indicates an arbitrary vector and matrix norm. The last inequality assures that the mapping
indicates an arbitrary vector and matrix norm. The last inequality assures that the mapping 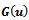 satisfies a Lipschitz condition on a bounded subset
satisfies a Lipschitz condition on a bounded subset 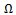 of
of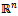 .
.5. Numerical Experiments
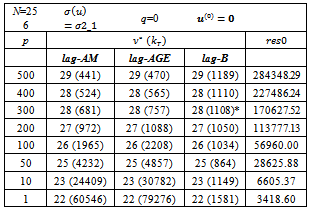
- In this section, we consider a numerical experimentation of the lagged diffusivity functional iteration method for the solution of the nonlinear system (4) generated by the finite difference discretization above described, of the elliptic problem (1)-(2). Indeed, we have to solve the system
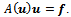 In these experiments, the vector solution
In these experiments, the vector solution 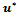 is prefixed and it is composed by the values of the prescribed function
is prefixed and it is composed by the values of the prescribed function 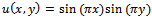 defined on the square
defined on the square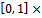
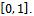 The chosen functions for
The chosen functions for 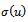 are
are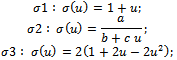 where, in the case of
where, in the case of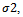 we have
we have 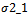 for a=3, b=2, c=1;
for a=3, b=2, c=1; 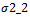 for a=1.5, b=0.1, c=0.9 and
for a=1.5, b=0.1, c=0.9 and 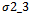 for a=1, b=0.01, c=0.99.The vector
for a=1, b=0.01, c=0.99.The vector 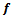 is computed as
is computed as 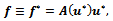 where the matrix
where the matrix 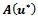 of order n, has elements as in (5) and (6) with N=M and
of order n, has elements as in (5) and (6) with N=M and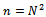 . In all the experiments we have N=256 and
. In all the experiments we have N=256 and 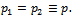 At each iteration
At each iteration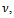
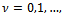 of the lagged diffusivity procedure, we have to solve the linear system of order n
of the lagged diffusivity procedure, we have to solve the linear system of order n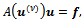 with the splitting method of the Arithmetic Mean or of the Alternating Group Explicit described in a previous section (see e.g.[9],[10] for an evaluation of the block form of the Arithmetic Mean method on different parallel architectures and[7] for a description of the Fortran code implementing the method). These methods are compared with BiCG-STAB method implemented as in[14, p. 50].We call
with the splitting method of the Arithmetic Mean or of the Alternating Group Explicit described in a previous section (see e.g.[9],[10] for an evaluation of the block form of the Arithmetic Mean method on different parallel architectures and[7] for a description of the Fortran code implementing the method). These methods are compared with BiCG-STAB method implemented as in[14, p. 50].We call 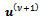 the new iteration of the lagged diffusivity procedure, computed with
the new iteration of the lagged diffusivity procedure, computed with 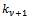 iterations of the inner solver such that the inner residual
iterations of the inner solver such that the inner residual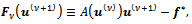 satisfies the condition (9)
satisfies the condition (9)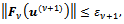 with
with 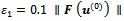 and
and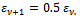 | (22) |
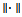 indicates the Euclidean norm. The vector
indicates the Euclidean norm. The vector 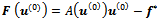 is the initial outer residual and its Euclidean norm is called
is the initial outer residual and its Euclidean norm is called 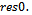 The initial vector
The initial vector 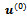 is taken as the null vector
is taken as the null vector 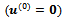 or as the vector e whose all the components are equal to 1
or as the vector e whose all the components are equal to 1 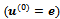 .The lagged diffusivity procedure has been implemented in a Fortran code with machine precision
.The lagged diffusivity procedure has been implemented in a Fortran code with machine precision 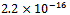 and stops when (10) holds, i.e., for
and stops when (10) holds, i.e., for 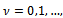
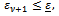 with
with 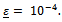 We call
We call 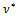 the iteration of the lagged diffusivity procedure for which condition (10) is satisfied. That is, the iterate
the iteration of the lagged diffusivity procedure for which condition (10) is satisfied. That is, the iterate 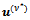 satisfies
satisfies 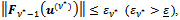 (and we have
(and we have 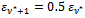 and
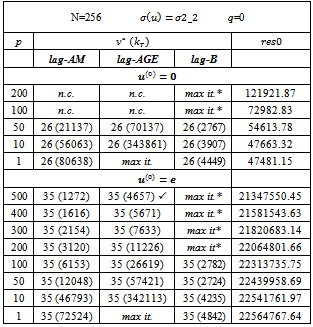
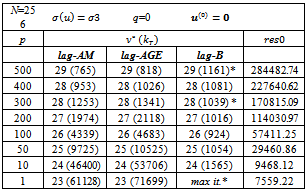
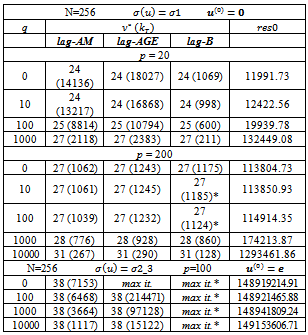
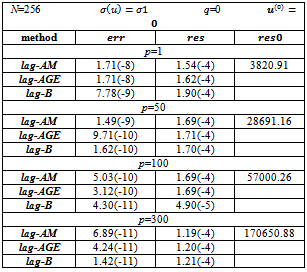
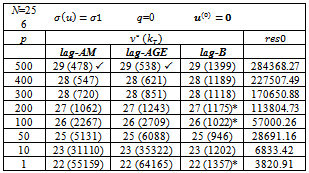
and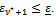 In the tables, we report the number of iterations
In the tables, we report the number of iterations 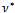 and, in brackets, the total number of iterations of the inner solver
and, in brackets, the total number of iterations of the inner solver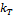 , i.e.,
, i.e.,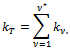 In the tables, we also report the discrete
In the tables, we also report the discrete 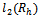 norm of the error,
norm of the error, 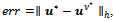 the Euclidean norm of the outer residual
the Euclidean norm of the outer residual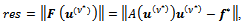 and
and 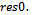 The symbol * close to the value of res indicates that the behaviour of the norm of the outer residual
The symbol * close to the value of res indicates that the behaviour of the norm of the outer residual  is not monotone decreasing.The writing max it. indicates that at a certain iteration v, the maximum number of iterations of the inner solver has been reached. The maximum number of inner iterations is set equal to 20000.The writing n.c. indicates that at a certain iteration v, the condition (7) is not satisfied.The symbol " ü " close to the number of inner and outer iterations denotes that at a certain iteration v , the condition (7) is not satisfied and, in these cases, the lagged diffusivity iteration method generates the iteration by performing a prefixed number (equal to 20) of iterations of the inner iterative solver.The writing 1.71(-8) indicates
is not monotone decreasing.The writing max it. indicates that at a certain iteration v, the maximum number of iterations of the inner solver has been reached. The maximum number of inner iterations is set equal to 20000.The writing n.c. indicates that at a certain iteration v, the condition (7) is not satisfied.The symbol " ü " close to the number of inner and outer iterations denotes that at a certain iteration v , the condition (7) is not satisfied and, in these cases, the lagged diffusivity iteration method generates the iteration by performing a prefixed number (equal to 20) of iterations of the inner iterative solver.The writing 1.71(-8) indicates 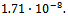 In the tables, we indicate with lag-AM, lag-AGE and lag-B, the lagged diffusivity functional iteration method with the Arithmetic Mean, the Alternating Group Explicit and the BiCG-STAB method, respectively, as inner solver.Furthermore, we observe that, since
In the tables, we indicate with lag-AM, lag-AGE and lag-B, the lagged diffusivity functional iteration method with the Arithmetic Mean, the Alternating Group Explicit and the BiCG-STAB method, respectively, as inner solver.Furthermore, we observe that, since 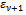 decreases, for v increasing, as (22) and the lagged diffusivity functional iteration method stops at the iteration
decreases, for v increasing, as (22) and the lagged diffusivity functional iteration method stops at the iteration 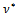 when the criterion for
when the criterion for 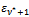 in (10) is satisfied, we have
in (10) is satisfied, we have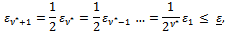 where we set
where we set 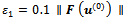 Then,
Then,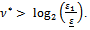 Indeed, in the experiments we obtain
Indeed, in the experiments we obtain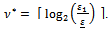
|
|
|
|
|
|
|
6. Conclusions
- From the numerical experiments the following conclusions can be drawn:● the outer residual res has the same order of
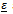 and the error err in the discrete
and the error err in the discrete 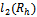 norm has, in worst cases, order
norm has, in worst cases, order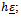 ● the AM method gives better results when the ratio between the maximum value of
● the AM method gives better results when the ratio between the maximum value of 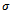 and the smallest component of
and the smallest component of 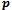 is small, that is the coefficient matrix of the linear system is strongly asymmetric (see[20]) or the deviation from asymmetry is decreasing. We define as the deviation from asymmetry of a matrix the difference between the Frobenius norms of the symmetric and nonsymmetric parts of the matrix. Furthermore, we can observe the same behaviour of the AGE method with the one of the AM method, respect to the deviation from asymmetry of the coefficient matrix that occurs at each step of the lagged diffusivity procedure;● the lagged diffusivity functional iteration method combined with the AM or the AGE method breaks down when the coefficient matrix, at a certain iteration v , is not an
is small, that is the coefficient matrix of the linear system is strongly asymmetric (see[20]) or the deviation from asymmetry is decreasing. We define as the deviation from asymmetry of a matrix the difference between the Frobenius norms of the symmetric and nonsymmetric parts of the matrix. Furthermore, we can observe the same behaviour of the AGE method with the one of the AM method, respect to the deviation from asymmetry of the coefficient matrix that occurs at each step of the lagged diffusivity procedure;● the lagged diffusivity functional iteration method combined with the AM or the AGE method breaks down when the coefficient matrix, at a certain iteration v , is not an 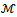 -matrix (n.c.). In some cases, the AGE inner solver, requires a large number of inner iterations especially for nearly symmetric matrices;● the behaviour of the residual res when we use AM or AGE method as inner solver, is always monotone, except in one case where the lagged diffusivity procedure breaks down (the coefficient matrix is not an
-matrix (n.c.). In some cases, the AGE inner solver, requires a large number of inner iterations especially for nearly symmetric matrices;● the behaviour of the residual res when we use AM or AGE method as inner solver, is always monotone, except in one case where the lagged diffusivity procedure breaks down (the coefficient matrix is not an 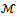 -matrix) but it has been possible to force the convergence by running a few number of iterations of the inner iterative solver. The nonmonotonicity of the residual happens at these "forced" iterations. This technique of forcing convergence is successful when condition (7) is "almost satisfied". ● the lagged diffusivity functional iteration method combined with the BiCG-STAB method, when it does not break down, requires a number of inner iterations that is not large and seems to be independent from the deviation from asymmetry of the coefficient matrix. We observe that the failure of the lagged diffusivity procedure with the BiCG-STAB method, in most cases, happens when the decreasing of the residual res is not monotone;● the behaviour of the lagged diffusivity procedure with AM or AGE method as iterative solver depends on the choice of the initial vector. The choice
-matrix) but it has been possible to force the convergence by running a few number of iterations of the inner iterative solver. The nonmonotonicity of the residual happens at these "forced" iterations. This technique of forcing convergence is successful when condition (7) is "almost satisfied". ● the lagged diffusivity functional iteration method combined with the BiCG-STAB method, when it does not break down, requires a number of inner iterations that is not large and seems to be independent from the deviation from asymmetry of the coefficient matrix. We observe that the failure of the lagged diffusivity procedure with the BiCG-STAB method, in most cases, happens when the decreasing of the residual res is not monotone;● the behaviour of the lagged diffusivity procedure with AM or AGE method as iterative solver depends on the choice of the initial vector. The choice 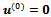 in the cases
in the cases 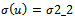 or
or 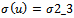 yields to negative values for
yields to negative values for 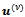 for a certain v (tipically
for a certain v (tipically 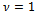 or
or 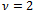 ) so that condition (7) is not satisfied; that is the initial iterate is too close to a region where a sufficient condition for determining the iterates of the outer procedure is not satisfied. Then, the control on condition (7) is a detection to start from another initial vector.
) so that condition (7) is not satisfied; that is the initial iterate is too close to a region where a sufficient condition for determining the iterates of the outer procedure is not satisfied. Then, the control on condition (7) is a detection to start from another initial vector. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML
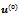 for
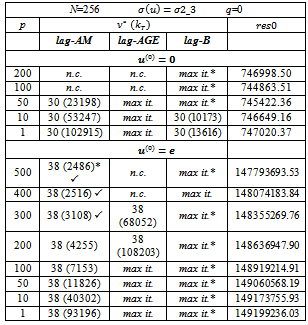
for