M.O Olayiwola 1, F.O Akinpelu 2, A.W Gbolagade 1
1Department of Mathematical & Physical Sciences, College of Science Engineering & Technology, Osun State University, Osogbo, Nigeria
2Department of Pure & Applied Mathematics,Faculty of Pure & Applied Sciences, Ladoke Akintola University of Technology, Ogbomoso, Nigeria
Correspondence to: M.O Olayiwola , Department of Mathematical & Physical Sciences, College of Science Engineering & Technology, Osun State University, Osogbo, Nigeria.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
In this paper, a Modified Variational Iteration Method (MVIM) for the solution of a differential equation of Bratu-type is presented. The method converges to the exact solution after an iteration. This shows that the method is efficient for this class of initial and boundary value problems.
Keywords:
Modified Variational Iteration Method, Lagrange Multiplier, Taylor’s Series, Bratu-type Differential Equation
Cite this paper:
M.O Olayiwola , F.O Akinpelu , A.W Gbolagade , "Modified Variational Iteration Method for the Solution of a Class of Differential Equations", American Journal of Computational and Applied Mathematics , Vol. 2 No. 5, 2012, pp. 228-231. doi: 10.5923/j.ajcam.20120205.05.
1. Introduction
Differential equations as a subject are a deductive science and a branch of Mathematics which have strong roots in physical problems such as Physics and Engineering. This subject also derives much of its power and beauty from the variety of its applicationsThis equations play a crucial role in applied mathematics and physics. The results of solving such equations can guide authors to know the described process deeply. But it is difficult to obtain the exact solution for some of these problems. In recent decades, there has been great development in the numerical methods for the solution of ordinary and partial linear and nonlinear differential equations. Bratu-type differential equation is an initial and boundary value problem in one-dimensional planar coordinate. It is used to model a combustion problem in a slab such as fuel ignition of the thermal combustion theory and in the Chandrasekhar model of the expansion of the universe[11]. It also used to simulate a thermal reaction process in a rigid material where the process depends on the balance between chemically generated heat and heat transfer by conduction.The Bratu-type is of the form: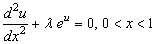 | (1) |
The exact solution is 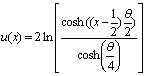 | (2) |
Where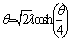 | (3) |
The equation has zero, one or two solution when 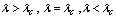 respectively. The
respectively. The 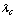 is the critical value which satisfies
is the critical value which satisfies 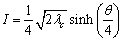 | (4) |
It has been shown that 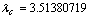 see[1,11,12]Several authors have presented various numerical approach to the solution of Bratu-type differential equations[1,2,6,11,12]. The variational iteration method was proposed by J.H He[4-5]. In this paper a Modivied Variational Iteration Method proposed by Olayiwola M O[7-9] is presented for the solution of Bratu-type differential equation. MVIM is the combination of VIM and the Taylor’s polynomial.
see[1,11,12]Several authors have presented various numerical approach to the solution of Bratu-type differential equations[1,2,6,11,12]. The variational iteration method was proposed by J.H He[4-5]. In this paper a Modivied Variational Iteration Method proposed by Olayiwola M O[7-9] is presented for the solution of Bratu-type differential equation. MVIM is the combination of VIM and the Taylor’s polynomial.
2. Variational Iteration Method
To illustrate the basic concept of the VIM, we consider the following general nonlinear partial differential equation.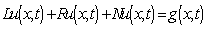 | (5) |
where L is a linear time derivative operator, R is a linear operator which has partial derivative with respect to x, N is a nonlinear operator and g is an inhomogeneous term. According to VIM, we can construct a correct fractional as follows: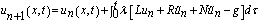 | (6) |
where 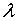 is a Lagrange multiplier which can be identified optimally via variational iteration method. The subscript n denote the nth approximation,
is a Lagrange multiplier which can be identified optimally via variational iteration method. The subscript n denote the nth approximation, 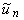 is considered as a restricted variation i.e,
is considered as a restricted variation i.e, 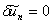 . The successive approximation
. The successive approximation 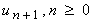 of the solution
of the solution 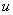 will be readily obtained upon using the determined Lagrange multiplier and any selective function
will be readily obtained upon using the determined Lagrange multiplier and any selective function 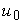 , consequently, the solution is given by:
, consequently, the solution is given by: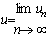 | (7) |
In Modified Variational Iteration Method, equation (6.0) becomes: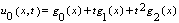 | (8) |
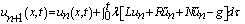 | (9) |
where 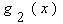 can be found by substituting for
can be found by substituting for 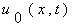 in (5.0) when
in (5.0) when 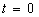 .
.
3. Stationary Conditions
The simplest problem of the calculus of variation is to determine a function: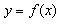 | (10) |
for which the value of a given functional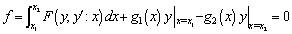 | (11) |
is a minimum or maximum.The extremum condition (stationary condition) of the functional (11) requires that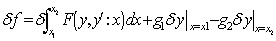 | (12) |
For arbitrary 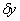 , we have
, we have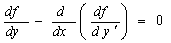 | (13) |
and the boundary conditions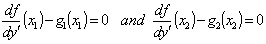 | (14) |
4. Derivation of 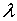
Consider (9) of the form:Making (15) stationary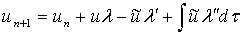 | (16) |
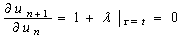 | (17) |
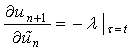 | (18) |
Solving (17-18), we have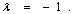 | (19) |
Consider equation (9) of the form: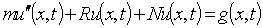 | (20) |
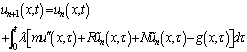 | (21) |
Making (21) stationary, we have: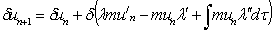 | (22) |
This yields the following stationary condition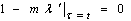 | (23) |
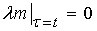 | (24) |
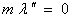 | (25) |
Solving (23-25), we have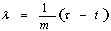 | (26) |
Equation (21) becomes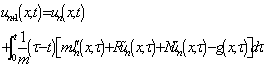 | (27) |
5. Convergence of the MVIM
Let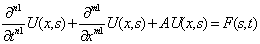 | (28) |
Theorem 1: Let 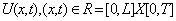 be the exact solution of (9) and
be the exact solution of (9) and  be the solution of the sequence
be the solution of the sequence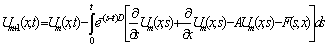 With
With 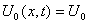 If
If 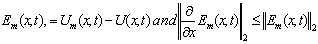 then the functional sequence
then the functional sequence 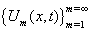 converges to
converges to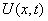 [10].Theorem 2: Taylor’s Theorem:A polynomial is a function of the form:
[10].Theorem 2: Taylor’s Theorem:A polynomial is a function of the form: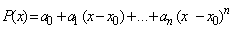 Where
Where 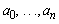 and
and 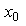 are constants. The polynomial is said to be written in powers of
are constants. The polynomial is said to be written in powers of 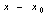 , and is of degree
, and is of degree 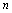 if
if 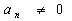 Lemma 1: If
Lemma 1: If 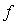 is differentiable at
is differentiable at 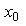 , then
, then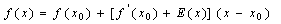 where
where 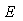 is defined on a neighborhood of
is defined on a neighborhood of 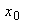 and
and 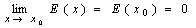 Theorem 3: If
Theorem 3: If 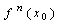 exists for some integer
exists for some integer 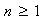 and
and 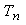 is the
is the 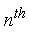 Taylor polynomial of
Taylor polynomial of 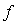 about
about 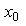 ,then the limit exists.Since Taylor’s series converges and VIM converges, then MVIM converges.
,then the limit exists.Since Taylor’s series converges and VIM converges, then MVIM converges.
6. Application of MVIM
We present a more stable and reliable method for the solution of the form: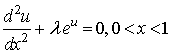 | (29) |
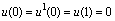 Where
Where 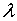 can take any value.Applying (8.0 - 9.0) in ( 10.0) we have
can take any value.Applying (8.0 - 9.0) in ( 10.0) we have 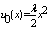 | (30) |
Using Maple to implement MVIM, we obtained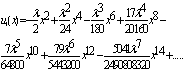 | (31) |
Test Case 1: Vahidi and Hasanzade[2] considered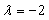 . The problem becomes:
. The problem becomes: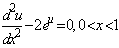 | (32) |
Vahidi and Hasanzade[2]. (11.0) becomes: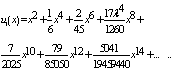 | (33) |
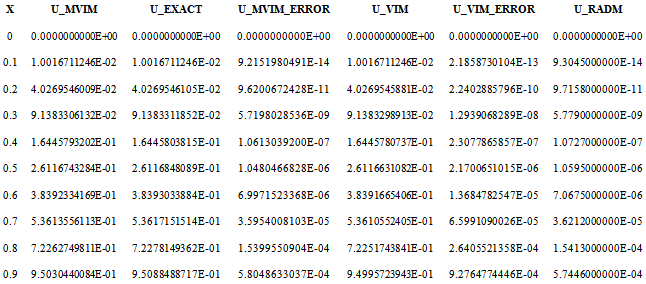
Table 1. Error comparison of the methods
 |
| |
|
The table above shows the comparison of result obtained by Vahidi[2]  , Noor and Mohyud-Din[6]
, Noor and Mohyud-Din[6] 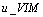 and
and 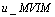 .with the exact solution
.with the exact solution 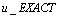 Test Case 2:Noor and Mohyud-Din[6], considerd:
Test Case 2:Noor and Mohyud-Din[6], considerd: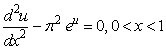 | (34) |
where 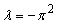 This gives:
This gives: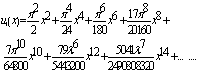 | (35) |
Test Case 3:Noor and Mohyud-Din[6], considerd: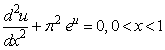 | (36) |
where 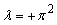 This gives:
This gives: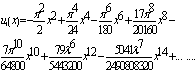 | (37) |
The exact solutions for (13.0, 15.0, 17.0) are: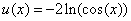 | (38) |
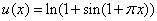 | (39) |
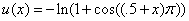 | (40) |
7. Conclusions
In this study, we have shown that the modified variational iteration method can be successfully applied for finding the solution of a class of differential eqution.The above table is the comparison of the error results of MVIM result after two iteration, the Noor[6] after six iteration and Vahid[2] after five iteration.The method does not involved the introduction of any set of algebraic equations that will be solved for another set of variables. The other two cases also converges to the exact solution.The result shows that the MVIM is a novel approach to the solution of Bratu-type differential equations.
ACKNOWLEDGEMENTS
Dr. M.O Olayiwola is highly grateful to the Tertiary Education Trust Funds-Education Trust Funds through Osun State University, Osogbo, Nigeria for the provision of grants for this research and also to Prof. Dr. Ji-Huan He, Soochow University China for his assistance in various forms.
References
| [1] | A.M Wazwaz, “Adomian decomposition method for a reliable treatment of the bratu-type equations”, App Maths Comput, vol.166 , pp652-663,2005. |
| [2] | A.R Vahidi , M Hasanzade, “ Restarted Adomians Decomposition method for the Bratu-type problem”, Applied mathematical Sciences, vol. 6, no. 10, pp479-486, 2012 |
| [3] | F. O Akinpelu, M.O. Olayiwola, “ On the Numerical Solution of Viscously Damped Bernoulli Beam with Moving Loads”,Advances in Differential Equations and Control Process, vol. 8. no. 2, pp 111-125,2011. |
| [4] | Ji-Huan He, “ Variational Iteration method: a kind of non-linear analytical technique: Some examples”, Int. Journal of Non-linear mechanics, vol. 3494 ,pp699-708, 1999 |
| [5] | He. J.H ,”Variational iteration method for autonomous ordinary differential system” App. Maths and Computation, vol.114, pp115-123, 2000. |
| [6] | M.A Noor , S.T Mohyud-Din,”Variational iteration method for solving initial and Boundary value problems of bratu-type”, Application and Applied mathematics. Vol. 3 no.1 , pp89-99, 2008. |
| [7] | M.O. Olayiwola, A .W. Gbolagade , A .O .Adesanya ,”An Efficient Algorithm for Solving the Telegraph Equation”, Journal of the Nigerian Association of Mathematical Physics, vol. 16, pp 199-204, 2010. |
| [8] | M.O. Olayiwola, A .W. Gbolagade and A .O .Adesanya (2010)- Solving Variable Coefficient Fourth-Order Parabolic Equation by Modified initial guess Variational Iteration Method (Journal of the Nigerian Association of Mathematical Physics Vol. 16, 2010,Pp 205-210) |
| [9] | M.O. Olayiwola, A .W. Gbolagade , F. O Akinpelu “ An Efficient Algorithm for Solving the Nonlinear PDE”, International Journal of Scientific and Engineering Research, vol. 2. issue 10, pp 1-10, 2011. |
| [10] | M.Tatari M,and M Delighan. ”On the convergence of He’s Variational iteration method” Journal of computational and applied Mathematics 207 (1) 121-128,2007. |
| [11] | R. Buckmire, “ Investigation of nonstandard Mickens-type finite difference scheme for singular boundary value problems in cylindrical or spherical coordinates”, Numerical methods for partial differential equations 19(3) pp380-398, 2003. |
| [12] | S.A Khuri,” A new approach to Bratu’s problem”, Applied mathematics and Computation , vol. 147, pp131-136, 2004. |
| [13] | U.M Aschar, R. Matheij , R.D Russell “Numerical solution of boundary value problems for ordinary differential equations”, SIAM, Philadelphia. P.A, 1995. |

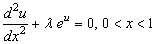
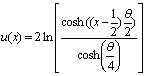
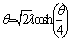
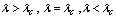 respectively. The
respectively. The 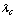 is the critical value which satisfies
is the critical value which satisfies 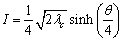
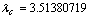 see[1,11,12]Several authors have presented various numerical approach to the solution of Bratu-type differential equations[1,2,6,11,12]. The variational iteration method was proposed by J.H He[4-5]. In this paper a Modivied Variational Iteration Method proposed by Olayiwola M O[7-9] is presented for the solution of Bratu-type differential equation. MVIM is the combination of VIM and the Taylor’s polynomial.
see[1,11,12]Several authors have presented various numerical approach to the solution of Bratu-type differential equations[1,2,6,11,12]. The variational iteration method was proposed by J.H He[4-5]. In this paper a Modivied Variational Iteration Method proposed by Olayiwola M O[7-9] is presented for the solution of Bratu-type differential equation. MVIM is the combination of VIM and the Taylor’s polynomial.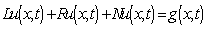
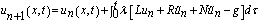
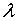 is a Lagrange multiplier which can be identified optimally via variational iteration method. The subscript n denote the nth approximation,
is a Lagrange multiplier which can be identified optimally via variational iteration method. The subscript n denote the nth approximation, 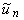 is considered as a restricted variation i.e,
is considered as a restricted variation i.e, 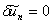 . The successive approximation
. The successive approximation 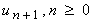 of the solution
of the solution 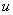 will be readily obtained upon using the determined Lagrange multiplier and any selective function
will be readily obtained upon using the determined Lagrange multiplier and any selective function 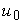 , consequently, the solution is given by:
, consequently, the solution is given by: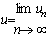
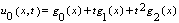
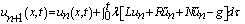
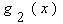 can be found by substituting for
can be found by substituting for 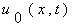 in (5.0) when
in (5.0) when 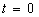 .
.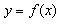
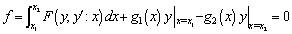
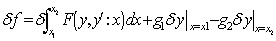
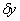 , we have
, we have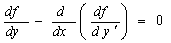
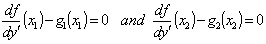
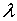
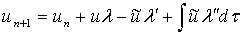
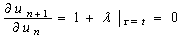
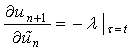
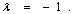
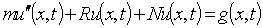
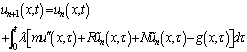
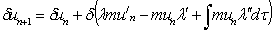
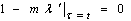
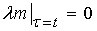
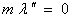
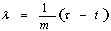
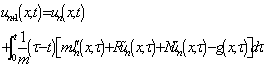
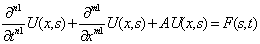
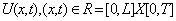 be the exact solution of (9) and
be the exact solution of (9) and 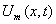 be the solution of the sequence
be the solution of the sequence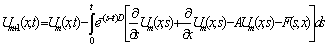 With
With 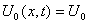 If
If 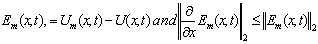 then the functional sequence
then the functional sequence 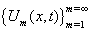 converges to
converges to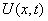 [10].Theorem 2: Taylor’s Theorem:A polynomial is a function of the form:
[10].Theorem 2: Taylor’s Theorem:A polynomial is a function of the form: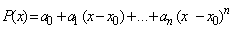 Where
Where 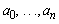 and
and 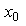 are constants. The polynomial is said to be written in powers of
are constants. The polynomial is said to be written in powers of 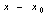 , and is of degree
, and is of degree 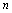 if
if 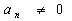 Lemma 1: If
Lemma 1: If 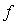 is differentiable at
is differentiable at 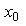 , then
, then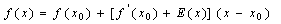 where
where 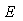 is defined on a neighborhood of
is defined on a neighborhood of 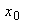 and
and 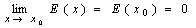 Theorem 3: If
Theorem 3: If 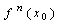 exists for some integer
exists for some integer 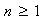 and
and 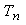 is the
is the 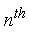 Taylor polynomial of
Taylor polynomial of 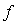 about
about 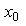 ,then the limit exists.Since Taylor’s series converges and VIM converges, then MVIM converges.
,then the limit exists.Since Taylor’s series converges and VIM converges, then MVIM converges.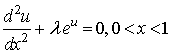
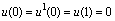 Where
Where 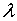 can take any value.Applying (8.0 - 9.0) in ( 10.0) we have
can take any value.Applying (8.0 - 9.0) in ( 10.0) we have 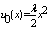
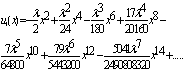
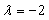 . The problem becomes:
. The problem becomes: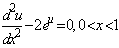
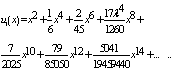
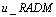 , Noor and Mohyud-Din[6]
, Noor and Mohyud-Din[6] 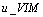 and
and 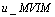 .with the exact solution
.with the exact solution 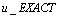 Test Case 2:Noor and Mohyud-Din[6], considerd:
Test Case 2:Noor and Mohyud-Din[6], considerd: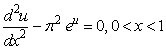
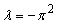 This gives:
This gives: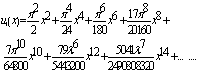
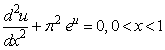
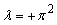 This gives:
This gives: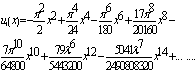
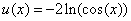
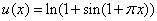
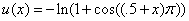
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML