| [1] | Y. Kuramoto, Chemical oscillations, waves and turbulence, Springer, Berlin, 1984. |
| [2] | G. Sivashinsky, On flame propagation under conditions of stoichiometry, SIAM Journal of Applied Mathematics, Vol.39, pp. 67-82, 1980. |
| [3] | G. I. Sivashinsky, Instabilities, pattern formation and turbulence in flames, Annual Review of Fluid Mechanics, Vol. 15, pp. 179-183, 1983. |
| [4] | G. I. Sivashinsky, D. M. Michelson, On irregular wary flow of a liquid film down a vertical plane, Progress of Theory Physics, Phys (Progress Lett.), Vol.63, pp. 2112-2114, 1980. |
| [5] | G. P. Agrawal, Nonlinear fiber Optics, 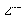 edition. Academic Press Inc. San Diego, 1995. edition. Academic Press Inc. San Diego, 1995. |
| [6] | J. H. B. Nijhof, N. J. Doran, W. Forysiak, F. M. Knox, Stable Soliton-like propagation in dispersion managed systems with net anomalous, zero and normal dispersion, Electronics Letters, Vol. 33, pp.1726-1727. |
| [7] | V. E. Zakharov, S. Wabnitz. Optical Solitons: Theoretical challenges and industrial perspectives: Springer- Verlag, 1998. |
| [8] | A. M. Wazwaz, the tanh method: Exact solutions of the sine-Gordon and the sinh-Gordon equations, Applied Mathematics and Computation Vol. 167, pp. 1196-1210, 2005. |
| [9] | A. M. Wazwaz, Partial differential equations: Methods and applications, Balkema, the Netherlands, 2002 |
| [10] | A. M. Wazwaz, Compactons dispersive structures for variants of the 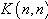 and the KP equations, Chaos Solitons, &Fractals, Vol.13, pp. 321-330, 2002. and the KP equations, Chaos Solitons, &Fractals, Vol.13, pp. 321-330, 2002. |
| [11] | A. M. Wazwaz, Exact specific solutions with solitary patterns for the nonlinear dispersive 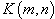 equations, Chaos, Solitons &Fractals, Vol.13, pp.161-170, 2001. equations, Chaos, Solitons &Fractals, Vol.13, pp.161-170, 2001. |
| [12] | A. M. Wazwaz, The tanh method for traveling wave solutions of nonlinear equations, Applied Mathematics and Computation, Vol. 133, pp. 213-227, 2002. |
| [13] | A. M. Wazwaz, A study of nonlinear dispersive equations with solitary wave solutions having compact support, Mathematics and Computers in Simulation, Vol.56, pp. 269-276, 2001. |
| [14] | H. Stendel , D. J. Kaup, Inverse scattering method applied to degenerate two-photon propagation in the law excitation limit, Journal of Physics A: Mathematical and Theoretical, Vol.33, pp. 1445-1457, 2000. |
| [15] | R. A. Fisher, W. K. Bischel, The role of linear dispersion in plane-wave self phase modulation, Journal of Applied Physics Letters, Vol. 23, pp. 661-663, 1973. |
| [16] | D. J. Kaup, T. I. Lakoba, Variational method: How it can generate false instabilities, Journal of Mathematical Physics, Vol.37, pp. 3442-3462, 1996. |
| [17] | D. J. Kaup, T. I. Lakoba, The squared eigenfunctions of the massive Thirring model in laboratory coordinates, Journal of Mathematical Physics, Vol. 37, pp. 308-323, 1996. |
| [18] | Qi Wang, Chen Yong, Hongqinq Zhang, A new jacobi elliptic function rational expansion method and its application to (1+1)-dimensional dispersive long wave equation, Chaos, Solitons & Fractals, Vol. 23, pp. 477-483, 2005. |
| [19] | He Ji Huan, Some asymptotic method for strongly nonlinear equations, International Journal of modern physics B, Vol. 20, pp. 1141-1199, 2006. |
| [20] | J. R. Bogning, T. C. Kofane, Analytical solutions of the discrete nonlinear Schrödinger equation in arrays of optical fibers Chaos, Solitons & Fractals, Vol. 28, pp. 148-153, 2006. |
| [21] | D. J. Kaup, T. I. Lakoba , Y. Matsuno, Perturbation theory for the Benjamin-Ono equation, Inverse Problems Vol.15, pp. 215-240, 1999. |
| [22] | E. Fan, extended tanh-function method and its applications to nonlinear equations, Physics Letters A, Vol. 277, pp. 212-218, 2000. |
| [23] | E. Fan, Y. C. Hon, Applications of extended tanh method to “special” types of nonlinear equations, Applied Mathematics and Computation, Vol. 141, pp. 351-358, 2003. |
| [24] | A. M. Wazwaz, the tanh-coth and the sine-cosine methods for kinks, solitons, and periodic solutions for the pochhammer-chree equations, Applied Mathematics and Computation, Vol.195, pp. 24-33, 2008. |
| [25] | E. Fan, C. H. Zhang, A note on the homogeneous balance method, physics Letters A, Vol. 246, pp. 403-406, 1998. |
| [26] | E. Fan, Two new applications of the homogeneous balance method, physics Letters A, Vol. 265, pp. 353-357, 2000. |
| [27] | J. H. He, X. H. Wu, Exp-function method for nonlinear wave equations, Chaos ,solitons &Fractals , Vol.30, pp. 700-708, 2006. |
| [28] | J. H. He, M. A. Abdou, New periodic solutions for nonlinear evolution equations using Exp-function method, Chaos, solitons & Fractal Vol. 34, pp. 1421-1429, 2007. |
| [29] | Xi-jun deng, periodic and solitary wave solutions in quadratic nonlinear media, Chinese Journal of Physics, Vol. 46, pp. 511-516, 2008. |
| [30] | W. Malfiet, the tanh method I: Exact solutions of nonlinear evolution and wave equations, American Journal of Physics, Vol. 4, pp. 650-654, 1992. |
| [31] | A. M. Wazwaz, compactons and solitary patterns structures for variants of the KdV and the KP equations, Applied Mathematics and Computation, Vol. 139, pp. 37-54, 2006. |
| [32] | L. Ji, C. X. Ping, Y. L. Jun, Soliton and periodic traveling wave solutions for quadratic nonlinear media, Chinese Physics Letters, Vol. 23, pp.147-150, 2006. |
| [33] | Clovis T Djeumen Tchaho, Jean R Bogning , Timoleon C Kofane, Construction of the analytical solitary wave solutions of modified Kuramoto-Sivashinsky equation by the method of identification of coefficients of the hyperbolic functions, Far East Journal of Dynamical Systems, Vol. 14, pp. 17-34, 2010. |
| [34] | Clovis T Djeumen Tchaho, Jean R Bogning , Timoleon C Kofane, Multi-Soliton solutions of the modified Kuramoto-Sivashinsky’s equation by the BDK method, Far East Journal of Dynamical Systems, Vol. 15, pp. 15(2), pp.83-98, 20011. |
| [35] | Jean R Bogning, Clovis T Djeumen Tchaho and Timoléon C Kofané. Construction of the soliton solutions of the Ginzburg- Landau equations by the Bogning-Djeumen Tchaho-Kofané method, Physica Scripta, Vol. 85, pp. 025013-025018, 2012. |
| [36] | Jean R Bogning, Clovis T Djeumen Tchaho, Timoléon C Kofane, Generalization of the Bogning- Djeumen Tchaho-Kofane Method for the construction of the solitary waves and the survey of the instabilities, Far East Journal of Dynamical Systems 2012 ( submitted) |

 . The essential thing is not to obtain of NPDEs, but to propose possible solutions. It is in this light that many resolution techniques have been proposed
. The essential thing is not to obtain of NPDEs, but to propose possible solutions. It is in this light that many resolution techniques have been proposed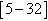 . In our recent works we proposed a new method of construction of solutions of NPDEs named the method of identification of coefficients of hyperbolic functions or Bogning-Djeumen Tchaho-Kofané method (BDKm)
. In our recent works we proposed a new method of construction of solutions of NPDEs named the method of identification of coefficients of hyperbolic functions or Bogning-Djeumen Tchaho-Kofané method (BDKm) 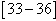 . In this work, we use the BDKm to construct the soliton solutions formed by combining solutions of type kink and pulse according to the degree of dominion of the parameter. It is necessary to say that here we are enlivened by the desire to construct a type of solitary wave solution that is the combination of several shapes of solitary waves. If we can already confess that on the mathematical plan it is possible, on the other hand we cannot already say explicitly what such a solution can represent in the practice or in the physics in general. While we think that in the case where the broadcast of such a signal would be possible in practice, it would be a solitary wave that will be able to change shape according to the characteristic properties of the propagation medium or merely of the met obstacle. To reach our goal, we needed a differential equation where cohabits the scattering and the non linearity. For this reason we chose a differential equation presenting a very strong non linearity. Thus, the construction of this multiform solution is supported by Kuramoto-Sivashinsky’s equation. This method has been chosen due to the fact that it is more adapted for the construction or amelioration of soliton solution in NPDEs.This work is organized as follows:In section 2, we are going to present the BDK method and in section 3 construct or propose a solution which is closer to the form envisaged. In section 4 we will polish up our work.
. In this work, we use the BDKm to construct the soliton solutions formed by combining solutions of type kink and pulse according to the degree of dominion of the parameter. It is necessary to say that here we are enlivened by the desire to construct a type of solitary wave solution that is the combination of several shapes of solitary waves. If we can already confess that on the mathematical plan it is possible, on the other hand we cannot already say explicitly what such a solution can represent in the practice or in the physics in general. While we think that in the case where the broadcast of such a signal would be possible in practice, it would be a solitary wave that will be able to change shape according to the characteristic properties of the propagation medium or merely of the met obstacle. To reach our goal, we needed a differential equation where cohabits the scattering and the non linearity. For this reason we chose a differential equation presenting a very strong non linearity. Thus, the construction of this multiform solution is supported by Kuramoto-Sivashinsky’s equation. This method has been chosen due to the fact that it is more adapted for the construction or amelioration of soliton solution in NPDEs.This work is organized as follows:In section 2, we are going to present the BDK method and in section 3 construct or propose a solution which is closer to the form envisaged. In section 4 we will polish up our work.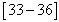
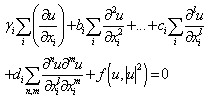
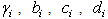 , are constants,
, are constants, 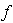 a linear function of
a linear function of 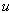 and
and 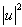 and
and 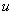 the variable to determine. Knowing that majority of soliton solutions have their analytic forms constituted by functions
the variable to determine. Knowing that majority of soliton solutions have their analytic forms constituted by functions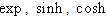 ,
, 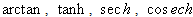 …, we have imagined the form of solutions capable of bringing together the different functions seen above. Among all general forms of solutions which have come across our minds, the most adapted is
…, we have imagined the form of solutions capable of bringing together the different functions seen above. Among all general forms of solutions which have come across our minds, the most adapted is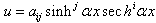
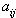 are constants to determine,
are constants to determine, 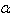 considered as known constant, i and j are natural integers. Why have we chosen solution (Eq.(2))? Simply because it covers effectively the majority of soliton solutions that we come across depending on the variation of integers i and j. The methodic principle is based on determining the constants
considered as known constant, i and j are natural integers. Why have we chosen solution (Eq.(2))? Simply because it covers effectively the majority of soliton solutions that we come across depending on the variation of integers i and j. The methodic principle is based on determining the constants 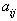 . If we propose the construction of solutions of Eq.(1) in the form
. If we propose the construction of solutions of Eq.(1) in the form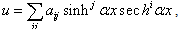
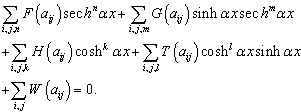
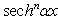 ,
, 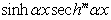 ,
, 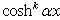 and
and 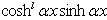 are considered as a sort of simple elements of Eq.(4). We wish simply to mention the fact that on introducing Eq.(3) in Eq.(1) we obtain hyperbolic functions which are not directly simple elements obtained in Eq.(4). To come back to the form Eq.(4), it is necessary to use adequate transformations
are considered as a sort of simple elements of Eq.(4). We wish simply to mention the fact that on introducing Eq.(3) in Eq.(1) we obtain hyperbolic functions which are not directly simple elements obtained in Eq.(4). To come back to the form Eq.(4), it is necessary to use adequate transformations  .On identifying the different coefficients of simple elements of Eq.(4) to zero, we obtain a range of equations in
.On identifying the different coefficients of simple elements of Eq.(4) to zero, we obtain a range of equations in  to determine. In all these equations those which have exact values and those which have values more or less closes to exact values respect a certain order of priority ( high value of n and m ). It is convenient to mention here that the choice of the solution to be made is fundamental. When the choice is not appropriate, the results will be contradictory.In the lines that follow we will go beyond the classical ways of calculation as seen in our previous works
to determine. In all these equations those which have exact values and those which have values more or less closes to exact values respect a certain order of priority ( high value of n and m ). It is convenient to mention here that the choice of the solution to be made is fundamental. When the choice is not appropriate, the results will be contradictory.In the lines that follow we will go beyond the classical ways of calculation as seen in our previous works  , construction of modulated soliton solution by the parameter
, construction of modulated soliton solution by the parameter 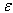 .
.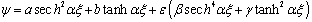 The modified Kuramoto-Sivashinsky’s equation is given by [33]
The modified Kuramoto-Sivashinsky’s equation is given by [33]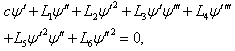
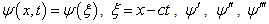 , and
, and 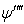 represent respectively the first derivative, the second derivative, the third derivative and the fourth derivative of
represent respectively the first derivative, the second derivative, the third derivative and the fourth derivative of 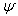 with respect to
with respect to 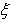 ,
, 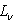 with
with 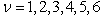 are the constants, the group velocity.The solutions of the shape
are the constants, the group velocity.The solutions of the shape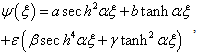
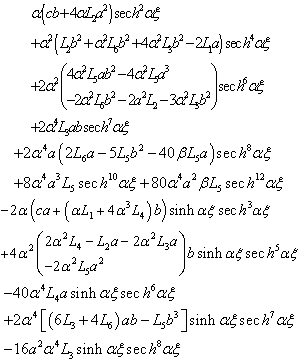

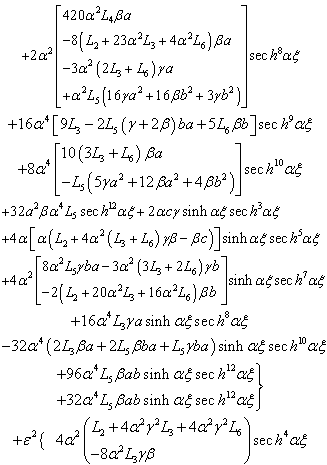

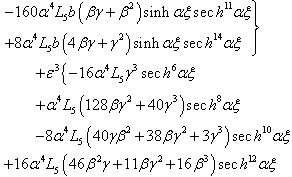
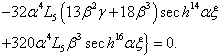
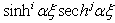 where
where 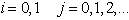 and according to the powers of
and according to the powers of 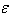 which is infinitely small, we getTerm in
which is infinitely small, we getTerm in 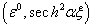 ,
,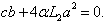
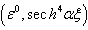 ,
,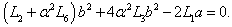
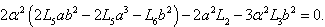
 ,
,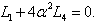
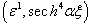 ,
,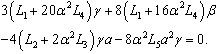
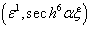 ,Term in
,Term in 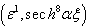 ,
,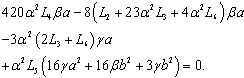
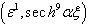 ,
,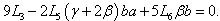
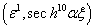 ,
,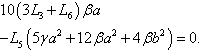
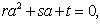
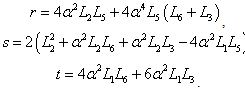 The resolution of Eq.(17) requires a discussion around the parameters r , s and t.For
The resolution of Eq.(17) requires a discussion around the parameters r , s and t.For 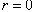 i.e.
i.e. 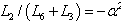 , Eq.(17) becomes an equation of second order and admits the solution
, Eq.(17) becomes an equation of second order and admits the solution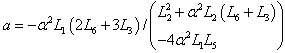
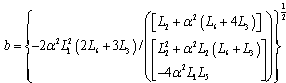
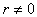 i.e.
i.e. 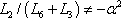 , Eq.(17) is of second order in a. The resolution of Eq.(17) in these conditions gives:For
, Eq.(17) is of second order in a. The resolution of Eq.(17) in these conditions gives:For 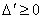 , we obtain the solution
, we obtain the solution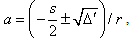
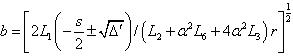
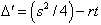 .- For
.- For 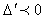 , we obtain the following roots
, we obtain the following roots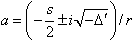
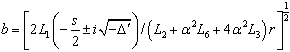
 and
and 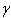 as functions of a and b
as functions of a and b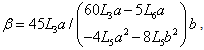
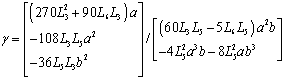
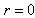 , i.e.
, i.e. 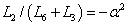 , the first family is given by
, the first family is given by 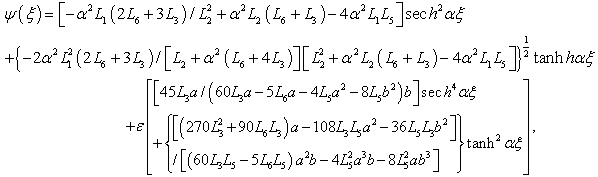
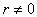 , i.e.
, i.e. 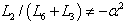 , we obtain the last two families of solutions
, we obtain the last two families of solutions 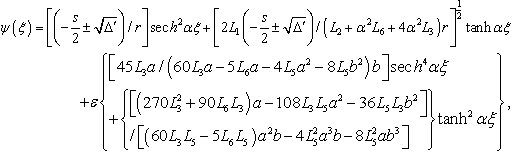
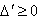 , a and bgiven by Eq.(22) and Eq.(23). We also have
, a and bgiven by Eq.(22) and Eq.(23). We also have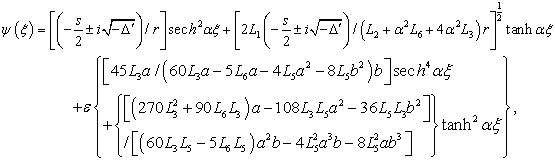
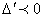 , a and bare given by Eq.(22) and Eq.(23).To better understand the notion of dominant and less dominant parts of wave
, a and bare given by Eq.(22) and Eq.(23).To better understand the notion of dominant and less dominant parts of wave 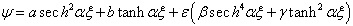 , we are engaged in the representation of the two main parts that constitute
, we are engaged in the representation of the two main parts that constitute 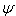 . If we state that
. If we state that 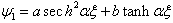 and
and 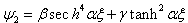 , the wave becomes
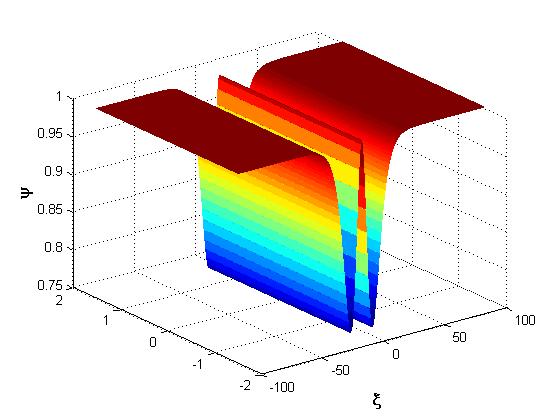
, the wave becomes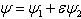 . Figure 1 shows the representation of
. Figure 1 shows the representation of 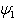 , which is the profile of a soliton wave of a kink type. Figure 2 and Figure 3 show the representation of
, which is the profile of a soliton wave of a kink type. Figure 2 and Figure 3 show the representation of 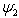 for a few values of
for a few values of 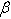 and
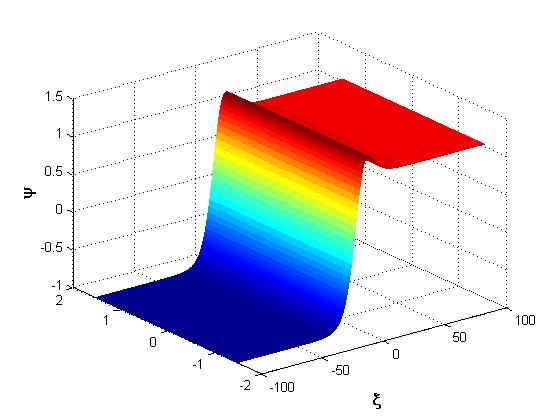
and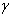 . The two profiles obtained in Figure 2 and Figure 3 are soliton waves of pulse nature. Figure 4 gives the representation of solution in general
. The two profiles obtained in Figure 2 and Figure 3 are soliton waves of pulse nature. Figure 4 gives the representation of solution in general 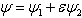 for
for 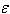 very small (). The profile obtained is that of a kink. We simply realize that
very small (). The profile obtained is that of a kink. We simply realize that 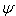 can take the form of a kink or the form of a pulse depending on the value of
can take the form of a kink or the form of a pulse depending on the value of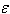 . As regard our research work, we have chosen for our dominant part
. As regard our research work, we have chosen for our dominant part 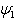 . The practical interpretation that we can give to this solution is that of a soliton wave solution which changes its form with respect to the environment in which it happens to be or to the obstacle to overcome in its medium of propagation. In the example considered hereafter the soliton
. The practical interpretation that we can give to this solution is that of a soliton wave solution which changes its form with respect to the environment in which it happens to be or to the obstacle to overcome in its medium of propagation. In the example considered hereafter the soliton 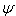 can lose its kink or pulse form depending on the conditions under which it is subjected.
can lose its kink or pulse form depending on the conditions under which it is subjected.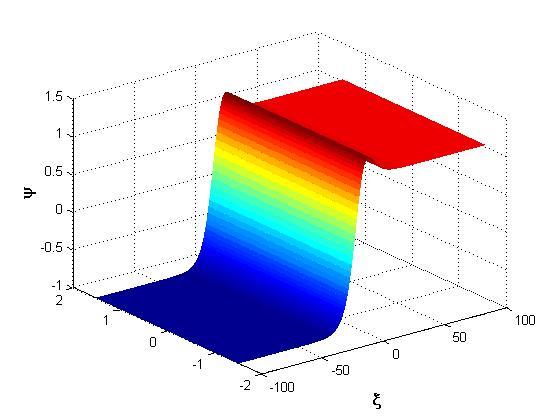
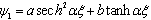 , for
, for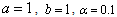
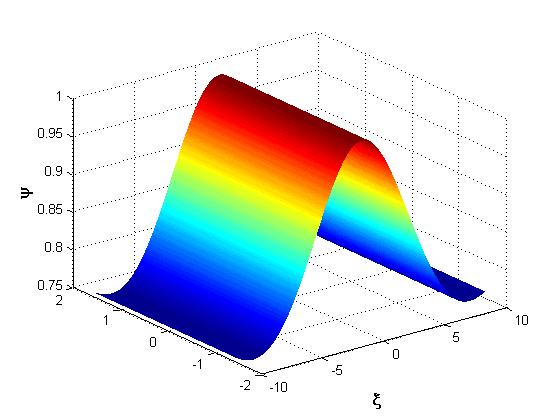
 , for
, for and and in the case where
and and in the case where
 , for
, for ,
,  ,
, 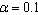 and in the case where
and in the case where 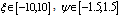
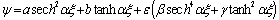 ,
, 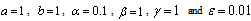
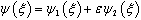 , where
, where 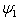 and
and 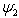 are solitary waves. Through the BDK innovative method mentioned above, we want to prove that it is possible to make up modulated soliton solutions of the form
are solitary waves. Through the BDK innovative method mentioned above, we want to prove that it is possible to make up modulated soliton solutions of the form 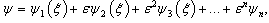 where
where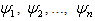 represent solitary waves. This form that we are putting forward as regard all calculations and analysis undertaken up to date, helps us to confirm our satisfaction as regard the usage of the BDK method in making up modulated soliton solution of Kuramoto-Sivashinsky’s equation.On the whole, projecting our reasoning rays beyond its limit, multi-soliton put into evidence experimentally will be an object of attraction for all scientists.
represent solitary waves. This form that we are putting forward as regard all calculations and analysis undertaken up to date, helps us to confirm our satisfaction as regard the usage of the BDK method in making up modulated soliton solution of Kuramoto-Sivashinsky’s equation.On the whole, projecting our reasoning rays beyond its limit, multi-soliton put into evidence experimentally will be an object of attraction for all scientists. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML edition. Academic Press Inc. San Diego, 1995.
edition. Academic Press Inc. San Diego, 1995. and the KP equations, Chaos Solitons, &Fractals, Vol.13, pp. 321-330, 2002.
and the KP equations, Chaos Solitons, &Fractals, Vol.13, pp. 321-330, 2002.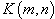 equations, Chaos, Solitons &Fractals, Vol.13, pp.161-170, 2001.
equations, Chaos, Solitons &Fractals, Vol.13, pp.161-170, 2001.