-
Paper Information
- Next Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Computational and Applied Mathematics
p-ISSN: 2165-8935 e-ISSN: 2165-8943
2012; 2(5): 197-205
doi: 10.5923/j.ajcam.20120205.01
Effect of Intermediate Toxic Product on the Survival of a Resource Dependent Species: A Modeling Study
1Department of Mathematics, H. B. Technological Institute, Kanpur, 208002, India
2Department of Mathematics, P.S. Institute of Technology, Bhauti, Kanpur, 208020, India
Correspondence to: Ram Naresh , Department of Mathematics, H. B. Technological Institute, Kanpur, 208002, India.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
A nonlinear model is proposed and analysed to study the effect of intermediate toxic product on the survival of a resource dependent species in a polluted environment. It is assumed that when resource biomass uptakes pollutants/toxicants, a liquid (sap) present in the body of biomass reacts with such toxicants and as such intermediate toxic product is formed. This toxic substance then affects the biomass and the species dependent on it. The analysis of the model shows that with increase in the cumulative emission rate of toxicants in the atmosphere, the densities of resource biomass and the species dependent on it decrease and attain their lowest equilibrium. If the rate of emission of toxicants is large enough, the resource biomass may become extinct under certain conditions and the species dependent on it may not survive. The model analysis also suggests that if the formation of intermediate toxic product is restricted by way of controlling the emission of toxicants in the environment, the resulting growth of resource biomass would lead to survival of species dependent on it.
Keywords: Resource Biomass, Resource Dependent Species, Intermediate Toxic Product, Stability, Numerical Simulation
Cite this paper: Ram Naresh , Shyam Sundar , "Effect of Intermediate Toxic Product on the Survival of a Resource Dependent Species: A Modeling Study", American Journal of Computational and Applied Mathematics , Vol. 2 No. 5, 2012, pp. 197-205. doi: 10.5923/j.ajcam.20120205.01.
Article Outline
1. Introduction
- Various kinds of pollutants/toxicants discharged into the environment very often affect the resources and the species dependent on them[1-14]. In particular, Freedman and Shukla[1] studied the effect of a toxicant on single species and predator-prey systems. They have assumed that the intrinsic growth rate of species decreases with increase in uptaken concentration of toxicant whereas its carrying capacity decreases with the environmental concentration of toxicant. The effect of toxicants on a two species competitive system was studied by Chattopadhyaya[2]. Samanta and Matti[3] studied the effect of toxicant on a single species by considering the three cases of toxicant emission i.e. instantaneous spill, constant emission and rapidly fluctuating random emission of toxicant into the environment. It was shown that the toxicant concentration emittedinstantaneously would not be sufficient to kill the population whereas the constant emission makes the population to settle down to steady state. In the third case (rapidly fluctuating random emission), the stability (local) of the system would depend on the washout rate of toxicant from the environment.In recent years, some mathematical models have also been proposed to study the existence and survival of resourcedependent species living in a polluted environment [15-21]. Dubey and Hussain[15] proposed models for the survival of two competing species dependent on a resource in an industrial environment. They assumed competing species to be partially dependent, wholly dependent or predating on the resource biomass. They concluded that an appropriate level of resource biomass can be maintained to ensure the survival of species if suitable efforts to conserve the resource biomass and to control the undesired label of industrialization pressure are made. Shukla et al.[16] studied a model for survival of resource dependent population to see the effect of toxicant emitted from external sources as well as formed by its precursors. They have shown that the densities of resource and the population decrease as the cumulative emission rate of environmental toxicant increases.It is pointed out here that in the above studies, the effect of toxicant on resource biomass and species dependent on it is considered but without incorporating the process of formation of intermediate toxic product. However, in real situations the intrinsic growth of resource biomass is, very often affected by intermediate toxic product which is formed inside the resource biomass due to some metabolic reactions. This resource biomass affected by the intermediate toxic product then affects the species dependent on it. In this direction, Naresh et al.[22] presented a mathematical model to study the effect of intermediate toxic product formed by uptake of a toxicant on plant biomass. They have shown that, as the rate of emission of toxicant increases, the equilibrium label of plant biomass decreases. Since the toxicants emitted into the atmosphere are uptaken by the resource biomass, an intermediate toxic product is formed which then affects the growth of resource biomass and the species dependent on it. Hence, in the present investigation, our main purpose is to study the effect of intermediate toxic product on the survival of resource dependent species. Thus, we propose a nonlinear mathematical model to see the effect of intermediate toxic product on the resource biomass and on the survival of species dependent on it[22].The paper is organized as follows, in Section 2 we present the mathematical model. The equilibrium analysis is carried out in Section 3 and in Section 4, the stability analysis of the model is presented. In Section 5, we present the numerical simulations of the model and conclusions are provided in Section 6.
2. Mathematical Model
- The following assumptions have been made in the modeling process,1. The densities of resource and species dependent on it are governed by logistic models.2. The growth rate of resource biomass decreases with increase in the concentration of intermediate toxic product.3. The growth rate of resource dependent species increases with increase in the density of resource biomass.4. The carrying capacities of resource biomass as well as that of species dependent on it decrease with environmental concentration of toxicants.Let
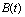 be the resource biomass density, affected by toxicants emitted at a constant rate
be the resource biomass density, affected by toxicants emitted at a constant rate 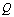 in the environment. It is assumed that, when the amount of toxicants uptaken by resource biomass interacts with the bio fluid (sap) present inside the biomass, an intermediate toxic product is formed which affects the growth of resource biomass. Let
in the environment. It is assumed that, when the amount of toxicants uptaken by resource biomass interacts with the bio fluid (sap) present inside the biomass, an intermediate toxic product is formed which affects the growth of resource biomass. Let 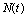 be the density of resource dependent species, its growth rate
be the density of resource dependent species, its growth rate 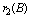 is enhanced by the resource biomass density. Let
is enhanced by the resource biomass density. Let 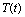 be the cumulative concentration of toxicants in the environment with natural depletion rate
be the cumulative concentration of toxicants in the environment with natural depletion rate 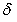 and
and 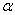 is the depletion rate coefficient of toxicants due to uptake by resource biomass. The environmental concentration of toxicants affect the carrying capacities
is the depletion rate coefficient of toxicants due to uptake by resource biomass. The environmental concentration of toxicants affect the carrying capacities 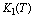 and
and 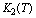 of the resource biomass and the resource dependent species respectively. It is assumed that the uptake of the toxicants by the resource biomass is directly proportional to the density of resource biomass and the concentration of toxicants. Let
of the resource biomass and the resource dependent species respectively. It is assumed that the uptake of the toxicants by the resource biomass is directly proportional to the density of resource biomass and the concentration of toxicants. Let 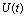 be the concentration of toxicants uptaken by the resource biomass with
be the concentration of toxicants uptaken by the resource biomass with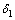 as natural depletion rate coefficient and
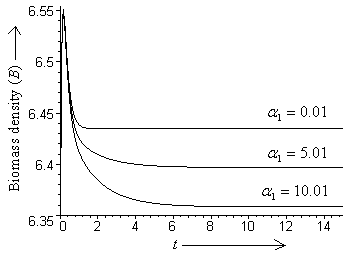
as natural depletion rate coefficient and 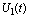 be the concentration of intermediate toxic product formed with a rate α1 and
be the concentration of intermediate toxic product formed with a rate α1 and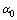 as its natural depletion rate coefficient.Keeping in view of the above assumptions and considerations, the system dynamics is assumed to be governed by the following nonlinear ordinary differential equations,
as its natural depletion rate coefficient.Keeping in view of the above assumptions and considerations, the system dynamics is assumed to be governed by the following nonlinear ordinary differential equations,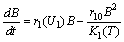 | (1) |
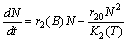 | (2) |
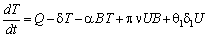 | (3) |
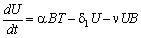 | (4) |
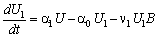 | (5) |
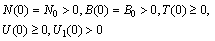 The uptaken concentration of toxicants and the concentration of intermediate toxic product are also assumed to be depleted by an amount
The uptaken concentration of toxicants and the concentration of intermediate toxic product are also assumed to be depleted by an amount 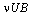 and
and 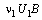 respectively due to falling of biomass on the ground. A fraction of the depleted amount
respectively due to falling of biomass on the ground. A fraction of the depleted amount 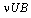
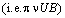 may also re-enter the environment, thus increasing the growth of toxicants. The constants
may also re-enter the environment, thus increasing the growth of toxicants. The constants 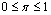 and
and 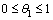 are reversible rate coefficients. All the constants are assumed to be non- negative.In the model, the function
are reversible rate coefficients. All the constants are assumed to be non- negative.In the model, the function 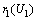 denotes the intrinsic growth rate of resource biomass which decreases as the concentration of intermediate toxic product
denotes the intrinsic growth rate of resource biomass which decreases as the concentration of intermediate toxic product 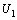 increases and hence, we assume that,
increases and hence, we assume that,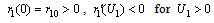 The function
The function 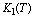 denotes the carrying capacity of resource biomass which decreases as the concentration of toxicant
denotes the carrying capacity of resource biomass which decreases as the concentration of toxicant 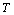 increases and hence,
increases and hence,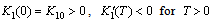 The function
The function 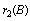 denotes the intrinsic growth rate of resource dependent species which increases as the resource biomass density
denotes the intrinsic growth rate of resource dependent species which increases as the resource biomass density 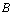 increases and hence,
increases and hence,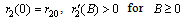 The function
The function 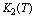 denotes the carrying capacity of resource biomass which decreases as the concentration of toxicant
denotes the carrying capacity of resource biomass which decreases as the concentration of toxicant 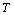 increases and hence,
increases and hence,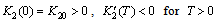
3. Equilibrium Analysis
- The model (1) – (5) has the following four equilibria namely,1.
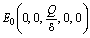 2.
2. 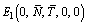 , where
, where 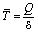 and
and 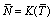 3.
3. 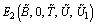 4.
4. 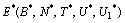 The existence of
The existence of 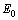 and
and 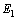 is obvious.
is obvious.3.1. Existence and Uniqueness of 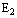
- The positive solution of variables in equilibrium
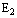 is given by the following equations which are obtained by putting the right hand sides of model equations (1) - (5) to zero
is given by the following equations which are obtained by putting the right hand sides of model equations (1) - (5) to zero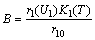 | (6) |
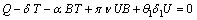 | (7) |
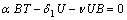 | (8) |
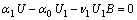 | (9) |
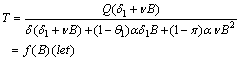 | (10) |
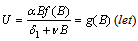 | (11) |
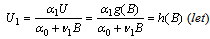 | (12) |
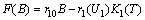 which gives
which gives 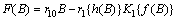 | (13) |
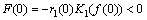 | (14) |
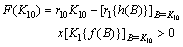 | (15) |
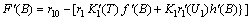 | (16) |
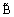 of
of 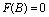 in
in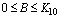 . The root will be unique, provided,
. The root will be unique, provided,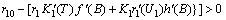 where,
where,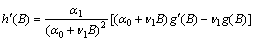
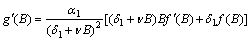
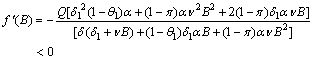 Knowing the value of
Knowing the value of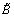 , the values of
, the values of 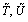 and
and 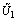 can be found from eqs. (10), (11) and (12) respectively.
can be found from eqs. (10), (11) and (12) respectively.3.2. Existence and Uniqueness of 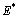
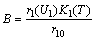 | (17) |
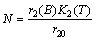 | (18) |
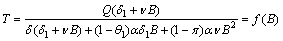 | (19) |
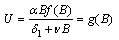 | (20) |
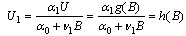 | (21) |
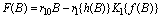 From this, it can be seen that
From this, it can be seen that 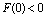 and
and 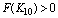 showing the existence of a root
showing the existence of a root 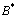 of
of 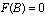 in
in 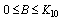 and the root will be unique, provided,
and the root will be unique, provided, 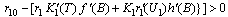 Knowing the value of
Knowing the value of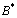 , we can find the values of
, we can find the values of 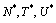 and
and 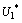 from eqs. (18), (19), (20) and (21) respectively.In the following we analyse the stability behavior of above equilibria.
from eqs. (18), (19), (20) and (21) respectively.In the following we analyse the stability behavior of above equilibria.4. Stability Analysis
- In this section, we describe stability analysis of different equilibria.Theorem 1(i) Equilibria
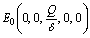 ,
, 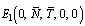 and
and 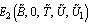 are unstable.(ii) If the following inequalities hold,
are unstable.(ii) If the following inequalities hold,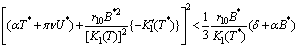 | (22) |
 | (23) |
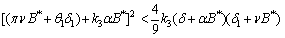 | (24) |
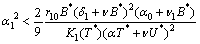 | (25) |
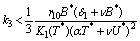 then
then 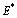 is locally asymptotically stable (See Appendix-A for proof).To establish the nonlinear asymptotic stability of
is locally asymptotically stable (See Appendix-A for proof).To establish the nonlinear asymptotic stability of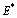 , we need the bounds of different variables. For this we propose the following region of attraction, stated without proof Freedman and So[23].Lemma 1 The set
, we need the bounds of different variables. For this we propose the following region of attraction, stated without proof Freedman and So[23].Lemma 1 The set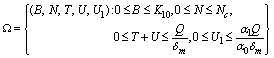 attracts all solutions initiating in the interior of non-negative octant, where
attracts all solutions initiating in the interior of non-negative octant, where 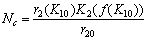 and
and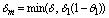 .Theorem 2.Let
.Theorem 2.Let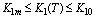 ,
,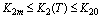 ,
, 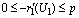 ,
, 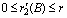 ,
,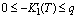 ,
,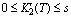 ,
, 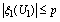 ,
, 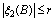 ,
, 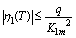 ,
, 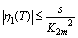 satisfying in
satisfying in  for some constants
for some constants 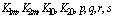 , then if the following inequalities hold in
, then if the following inequalities hold in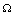 ,
,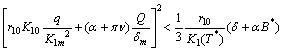 | (26) |
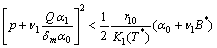 | (27) |
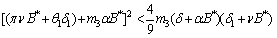 | (28) |
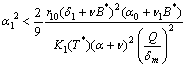 | (29) |
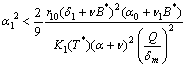
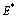 is nonlinearly asymptotically stable with respect to all solutions initiating in the interior of the first octant. (See Appendix-B for proof)1. If
is nonlinearly asymptotically stable with respect to all solutions initiating in the interior of the first octant. (See Appendix-B for proof)1. If 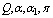 and
and 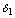 are very small, then the possibility of satisfying conditions (22) – (29) is more plausible showing that these parameters have destabilizing effect on the system.2. If
are very small, then the possibility of satisfying conditions (22) – (29) is more plausible showing that these parameters have destabilizing effect on the system.2. If 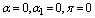 and
and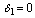 , then the conditions (24), (25), (28) and (29) are satisfied automatically.The above analysis imply that as the rate of introduction of toxicants in the environment increases, then under certain conditions the densities of resource biomass and resource dependent species decrease and settle down to their respective equilibrium levels. It is pointed here that the magnitude of equilibrium of species would mainly depend upon the resource biomass density affected by intermediate toxic product formed inside the biomass due to some metabolic changes. The density of resource biomass decreases as cumulative concentration of toxicants in the environment increases and it may even tend to zero for very high concentration of toxicants and then the species dependent on it may not survive.
, then the conditions (24), (25), (28) and (29) are satisfied automatically.The above analysis imply that as the rate of introduction of toxicants in the environment increases, then under certain conditions the densities of resource biomass and resource dependent species decrease and settle down to their respective equilibrium levels. It is pointed here that the magnitude of equilibrium of species would mainly depend upon the resource biomass density affected by intermediate toxic product formed inside the biomass due to some metabolic changes. The density of resource biomass decreases as cumulative concentration of toxicants in the environment increases and it may even tend to zero for very high concentration of toxicants and then the species dependent on it may not survive.5. Numerical Simulations
- In this section, we analyse the model (1) – (5) numerically with the help of MAPLE 7.0 to study the behaviour of the system for different values of parameters. For this we assume that,
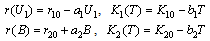 Now we consider the following set of parameter values,
Now we consider the following set of parameter values,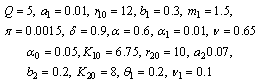 Equilibrium values of different variable in
Equilibrium values of different variable in  are obtained as,
are obtained as,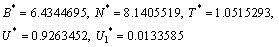 Eigen values of the matrix corresponding to
Eigen values of the matrix corresponding to 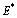 are given by,
are given by,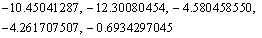 Since all the eigen values corresponding to
Since all the eigen values corresponding to 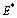 are negative and therefore
are negative and therefore 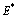 is locally asymptotically stable.The nonlinear asymptotic stability behaviour of
is locally asymptotically stable.The nonlinear asymptotic stability behaviour of 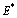 in
in 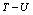 and
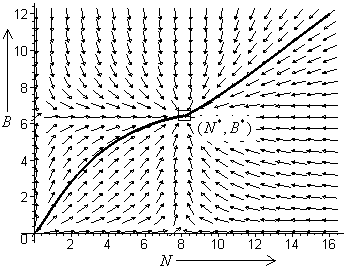
and 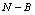 plane is shown in the figure 1 and figure 2 respectively. In these figures, it is shown that the trajectories started at any point in the region approaches the equilibrium point
plane is shown in the figure 1 and figure 2 respectively. In these figures, it is shown that the trajectories started at any point in the region approaches the equilibrium point 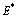 showing that the equilibrium is nonlinearly asymptotically stable. In figures 3, 4, 5, the variation of the densities of biomass (B), resource dependent species
showing that the equilibrium is nonlinearly asymptotically stable. In figures 3, 4, 5, the variation of the densities of biomass (B), resource dependent species 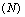 and the concentration of intermediate toxic product
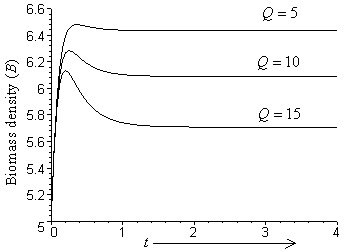
and the concentration of intermediate toxic product 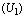 is shown with time at different values of rate of emission of toxicants in the environment i.e. at
is shown with time at different values of rate of emission of toxicants in the environment i.e. at 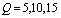 respectively. From these figures, it is observed that the densities of biomass and species dependent on it decrease as the rate of introduction of toxicants increases and settle down to their respective equilibrium levels, while the concentration of intermediate toxic product increases. In figures 6 and 7, the variation of the densities of biomass (B) and resource dependent species
respectively. From these figures, it is observed that the densities of biomass and species dependent on it decrease as the rate of introduction of toxicants increases and settle down to their respective equilibrium levels, while the concentration of intermediate toxic product increases. In figures 6 and 7, the variation of the densities of biomass (B) and resource dependent species 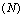 is shown with time at different values of rate of formation of intermediate toxic product
is shown with time at different values of rate of formation of intermediate toxic product 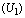 i.e. at
i.e. at 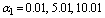 respectively. From these figures, it can be seen that the densities of biomass and species dependent on it decrease as the rate of formation of intermediate toxic product increases and settle down to their respective equilibrium levels. In figure 8, it is shown that if the growth of resource biomass increases, the density of species dependent on it also increases.
respectively. From these figures, it can be seen that the densities of biomass and species dependent on it decrease as the rate of formation of intermediate toxic product increases and settle down to their respective equilibrium levels. In figure 8, it is shown that if the growth of resource biomass increases, the density of species dependent on it also increases.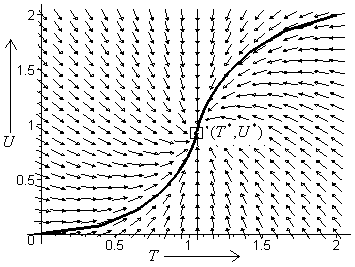 | Figure 1. Nonlinear stability in  plane plane |
 | Figure 2. Nonlinear stability in  plane plane |
 | Figure 3. Variation of biomass density B with time  for different values of for different values of 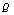 |
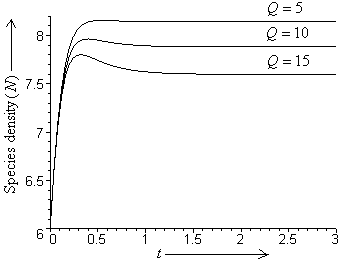 | Figure 4. Variation of density of resource dependent species 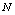 with time with time 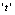 for different values of for different values of 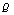 |
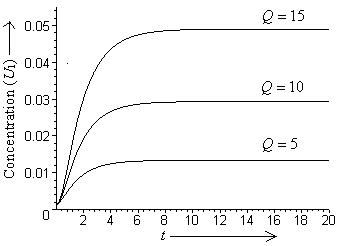 | Figure 5. Variation of concentration of intermediate toxic product 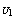 with time with time 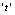 for different values of for different values of 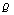 |
 | Figure 6. Variation of biomass density with time with time  for different values of for different values of 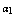 |
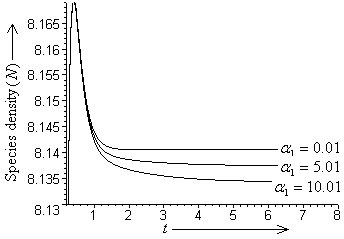 | Figure 7. Variation of density of resource dependent species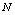 with time with time 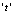 for different values of for different values of 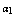 |
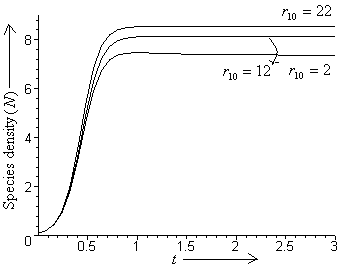 | Figure 8. Variation of density of resource dependent species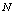 with time with time 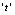 for different values of for different values of 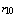 |
6. Conclusions
- In this paper, we have proposed a nonlinear mathematical model to study the effect of intermediate toxic product on the survival of a resource dependent species living in a polluted environment. It is assumed that the growth of resource biomass is affected by the intermediate toxic product formed inside the resource biomass due to some metabolic reactions when toxicants present in the environment are uptaken by resource biomass. This affected resource biomass by the intermediate toxic product then affects the resource dependent species. The model is analysed using stability theory of differential equations and computer simulations. It is shown that densities of resource biomass and species dependent on it decrease as the rate of introduction of toxicants increases in the environment and settle down to their respective equilibrium levels while the concentration of intermediate toxic product increases. Further, as the rate of formation of intermediate toxic product increases, the densities of resource biomass and the species dependent on it also decrease and their magnitudes are less than their respective densities when they are not affected by toxicant. If the rate of emission of toxicants in the environment is large enough, then under certain conditions the resource biomass may become extinct due to increased level of intermediate toxic product affecting the growth of biomass and as such the species dependent on it may not survive. It is also observed that the density of species dependent on resource biomass increases if the growth of resource biomass increases. Thus, if the formation of intermediate toxic product is restricted by way of controlling the emission of toxicants in the environment, the resulting growth of resource biomass would lead to survival of species dependent on it.
APPENDIX-A
- Proof of the Theorem 1.(i) The variational matrix corresponding to
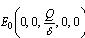 is given by,
is given by, It can be seen that the two eigen values
It can be seen that the two eigen values  of
of  are positive, therefore
are positive, therefore 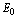 is a saddle point.The variational matrix corresponding to
is a saddle point.The variational matrix corresponding to 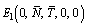 is given by,
is given by,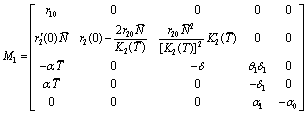 From which we note that
From which we note that 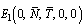 is a saddle point.Similarly, it can also be checked that equilibrium point
is a saddle point.Similarly, it can also be checked that equilibrium point 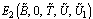 is unstable in
is unstable in  - direction.(ii) Consider the following positive definite function about
- direction.(ii) Consider the following positive definite function about 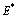 ,
,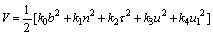 | (A1) |
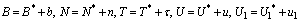 Differentiating (A1) with respect to
Differentiating (A1) with respect to 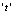 we get
we get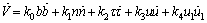 | (A2) |
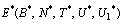 in (A2), we have,
in (A2), we have,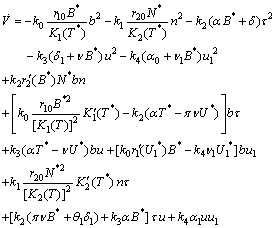 Now
Now 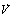 will be negative definite, if the following inequalities are satisfied,
will be negative definite, if the following inequalities are satisfied,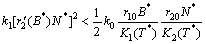 | (A3) |
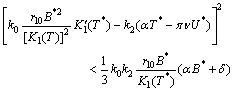 | (A4) |
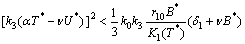 | (A5) |
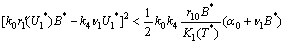 | (A6) |
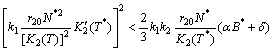 | (A7) |
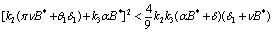 | (A8) |
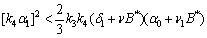 | (A9) |
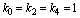 ,
,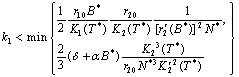
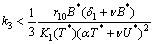
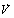 will be negative definite provided the conditions (22) – (25) are satisfied, showing that
will be negative definite provided the conditions (22) – (25) are satisfied, showing that 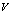 is a Liapunov function and hence
is a Liapunov function and hence 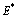 is locally asymptotically stable.
is locally asymptotically stable.APPENDIX-B
- Proof of the Theorem 2.Consider the following positive definite function about
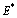
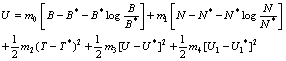 | (B1) |
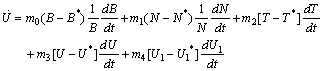
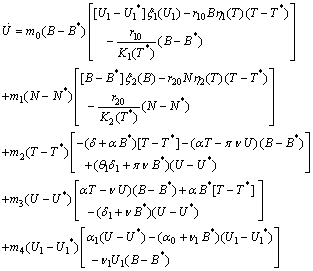 Where
Where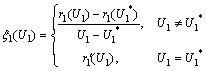
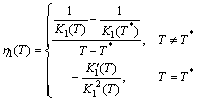
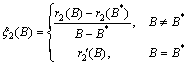
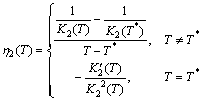
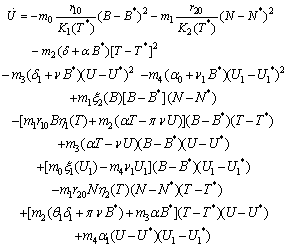 Now
Now 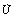 will be negative definite under the following sufficient conditions,
will be negative definite under the following sufficient conditions,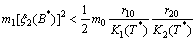 | (B2) |
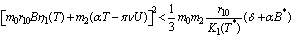 | (B3) |
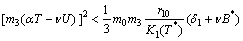 | (B4) |
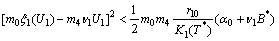 | (B5) |
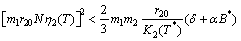 | (B6) |
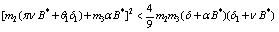 | (B7) |
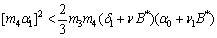 | (B8) |
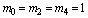 ,
,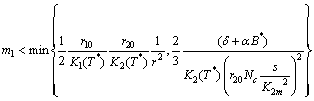
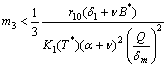
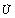 will be negative definite provided the conditions (26) – (29) are satisfied and hence the theorem.
will be negative definite provided the conditions (26) – (29) are satisfied and hence the theorem. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML