1. Introduction

Elements of any engineering structure independent of its purpose must be strong, rigid and light with the least consumption of material. So one of the basic problems of design is a study of stress − strain state in machine elements or structure elements of a given type and development, on the basis of carried out investigations, of new, more rational constructive forms.

In this connection, optimal design of spatial prismatic elements of a structure of arbitrary section of different buildings and study of their strength properties present actual tasks and demand an application of modern methods of design, which allow to account real conditions of operation, configuration of a given element with consideration of material properties.

Elements of a structure in a number of cases demand maximal weight decrease due to material consumption, caused by technology of fabrication (cavities, inclusions and depressions). These elements of a structure with geometrical features may present prismatic bodies with different configuration of section, which are described by the system of differential equations in partial derivatives of complex type. To solve them approximation methods of Bubnov − Galerkin or Ritz or Vlasov − Kantorovich type with boundary conditions are used. In their realization, one not always manages to build the system of coordinate functions, so to do it the method of R − functions[1, 14 −21] or finite elements method[2] or differential schemes[3] are used. In this paper the method of R − functions is used. The essence of this method consists in building of special coordinate succession of functions, which allows to satisfy boundary conditions at practically arbitrary geometry of domain[4].

2. Task Definition

To prove an algorithm of the procedure of R − function, we consider the problem of constraint torsion of prismatic bodies of arbitrary section in Cartesian system of coordinates (x, y, z). We will assume that one of sections (z=0) is fixed (u=v=w=0), and to another section (z=c) torsion moment is applied (М). Lateral sides are free from loads. If the body has cavities, its surface is also taken as free. An equation of balance for this body has the form:

(1)

(2)

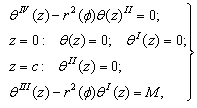
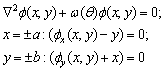
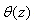where − is a torsion angle; 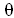^I − relative angle of twisting; φ(x,y) − torsion function; r²(φ)=(I_p+2I_d+I_k)/iφφ; M=M_кр/ Iφφ;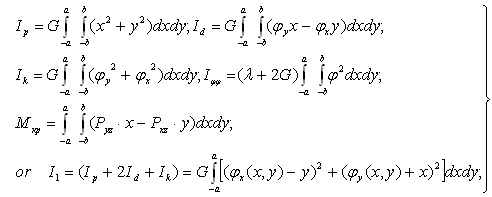

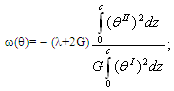
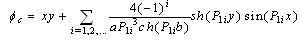
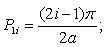(3)

(4)

G=Е/(2(1+μ)); λ=μE/((1−2μ)(1+μ)); P_yz, P_xz – are given loads, μ – Poisson coefficient; Е – elasticity modulus.

3. Solution Algorithm

Coefficients (3) correspond to a case when the section of a given body is solid and rectangular.

An algorithm of integration of equations with boundary conditions (1) and (2) corresponds to[5 −13]:

In the first step it is assumed that ω(θ) in (2) equals to zero and is solved by:

(5)

where

In the second step r²(φ) is calculated and is solved by (1):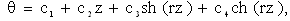

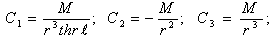
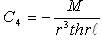(6)

where .

Then ω(θ) is calculated and is solved by (2):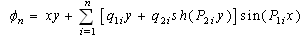

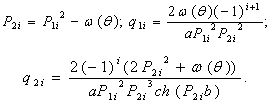(7)

where

Then the condition 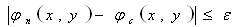is checked in a given points х and у. If the condition is satisfied, the components of displacement are calculated: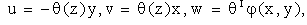

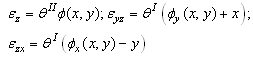
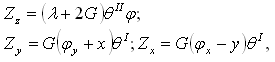
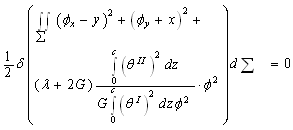
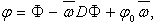
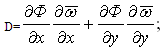
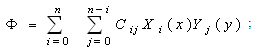
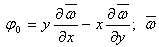(8)

strains

; (9)

stresses

(10)

If the conditions are not satisfied, the steps are repeated beginning from the second one.

If the section of a given body is of complex configuration or has cavities or depressions, the procedure of R − function by Bubnov − Galerkin method is used. To build the function φ(х, у) for described algorithm, the following functional is used:

(11)

Now we will consider for comparison the results of procedure of R - function in design of prismatic body of solid section under following conditions:

The problem was solved analytically (a.s.) and using the procedure of R − function (R s.) with solution structure

(12)

where

(13)

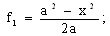
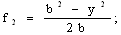
=f₁⊥₀f₂ − boundary form; 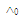− conjunction.

C_ij − are unknown coefficients to be defined; X_i(x), Y_j(y) − full system of basic polynomes (order ones, trigonometric, Chebyshev’s or other).

4. Experiment in Numbers

Results of design of torsion function and components of tensors of stresses are shown in Tables 1 and 2 for different section of body and for different values of х and у respectively.

In Tables 1 and 2 in each block the first line corresponds to zero solution in (5) and in R − function, and the following lines – to approximations.

As seen from the tables, in the third and fourth approximations the values of torsion function coincide by two signs; and in arbitrary on х and у by three signs in meaning figures. When the solution φ is built analytically for rectangular solid section with procedure R − function, they coincide up to the third sign of meaning figures. With decrease of the area of section of the body, its coincidence and convergence become better. So in approximation of the section to quadrate it is advisory to increase the number of terms in solutions. Table 2 shows the values of components of stresses and good agreement and convergence.

Now consider design of the body with rectangular cavity with the same values (а₁=a/10; b₁=b/10), the surfaces of cavities are free from loads. The structure of solution has the form (12), and forms of boundaries of section of a given body are determined by the following way:

, ,

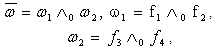where

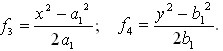In this case the following boundary conditions are added to (2):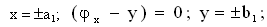

.

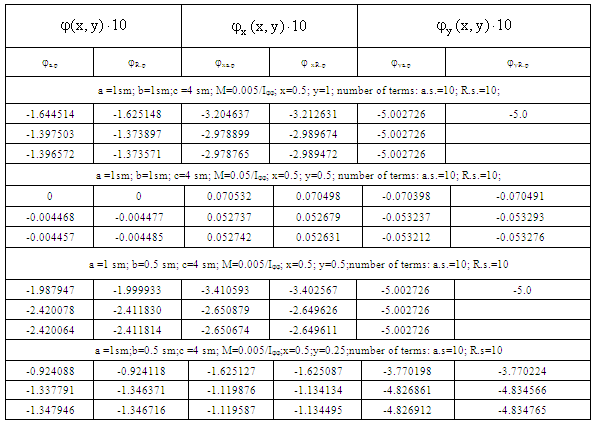
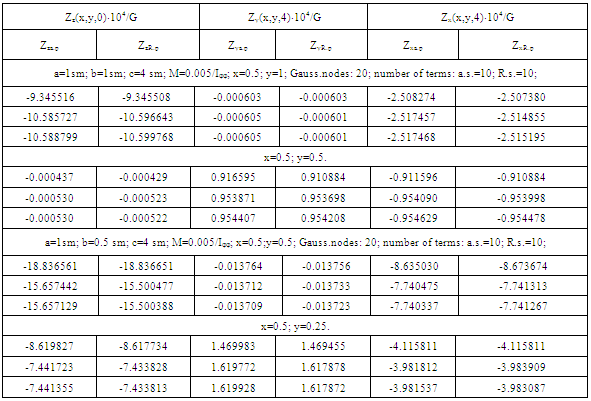
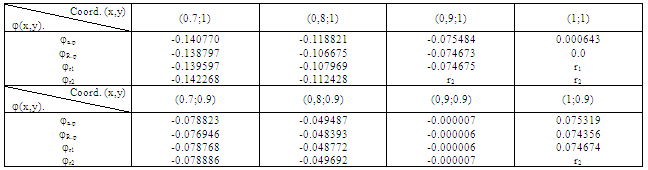
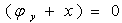Here numeric convergence of torsion function and its derivatives are studied; results are given in Table 3 for different number of terms in (13), where good agreement and convergence are observed for different sections of prismatic body with rectangular cavity.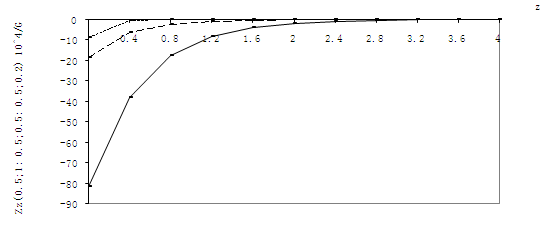

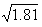Table 1. Results of torsion function and its derivatives in different points

Table 2. Results of components of tensors of stresses in different points

Table 3. Results of torsion function and its derivatives in different points

Decrease of the area of section and occurrence of cavity improve convergence of results, because the number of nodes and systems of coordinate functions are increasing.

With an increase of the length of body and decrease of the section of body the values of tangential stresses at z=с are increasing up to reaching the size of large side of section and then they transfer to parallel state to z axis. On the basis of results we may assume that procedure of R-function may be substantially applied in design of prismatic bodies with complex configuration of section.

Results show that the physics of the process in these prismatic bodies of rectangular section with rectangular cavity is correctly expressed. Because of the small value of cavity there is no great difference between the change of section in values of stresses for solid bodies and prismatic bodies with cavity. The change of curves (Z_z, Z_y,Z_x) along the length of body may be observed in Figures (1−3).

Table 4. Results of components of tensors of stresses in different points

Figure 1. The change of component Zz of stresses in different points

Figure 2. The change of component Zy of stresses in different points

In Figures 1, 2, 3 dotted, broken and solid lines correspond to the following dimensions of section: а=1sm, b=1sm; а=1sm, b=0.5sm; а=1sm, b=0.2sm. Curves are given for one and the same coordinate’s х and у, and external load. All curves qualitatively coincide with curves of design of prismatic body of solid section. The least value for normal stress is obtained for quadratic section, the greatest value – for narrow rectangular section; an increase of the length of body does not lead to sharp rise of stress values, step − by −step they increase up to the size of large side of section, then they tend to approximate to “z” − axis (Fig.1.) in normal stresses, and in tangential stresses are parallel to “z” − axis (Fig. 2,3).

Now consider the effect of angle points of quadratic section and quadratic cavity on numeric convergence of procedure of R − function.

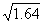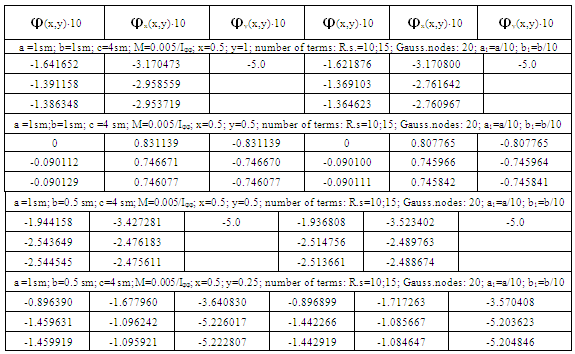
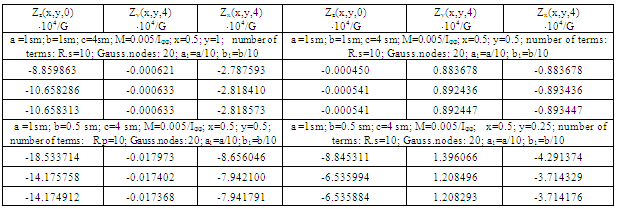
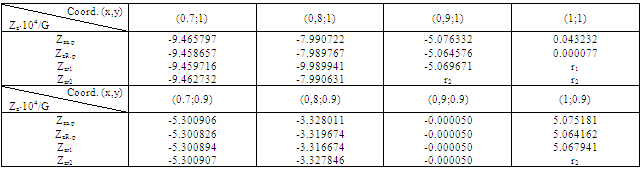
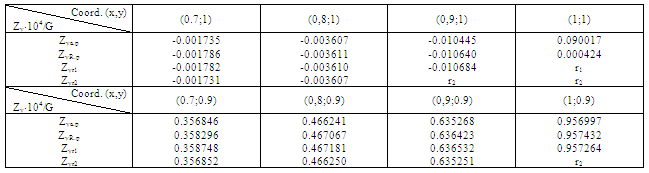
Consider prismatic body of solid quadratic section with rounded angles with the following values of radiuses r₁=0.1 (); r₂=0.2 (). In this case an equation of boundary will have the following form: 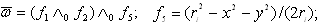i=1,2,3. Results of design are given in Table 5.

As seen from the Table near the angle the values of torsion function coincide in one figure, so results obtained earlier are correct. If the radius is less and the number of terms in the structure of solution of R − function is greater, the results will be better.

The values of components of tensor of stresses are given below (Tables 6, 7, 8):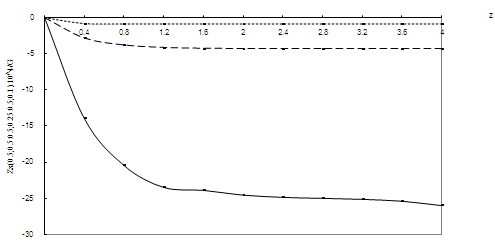

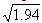Figure 3. The change of component Zx of stresses in different points

Table 5. Results of torsion function in different points

Table 6. Results of component of tensor of stresses Zz in different points

Table 7. Results of component of tensor of stresses Zx in different points

Table 8. Results of component of tensor of stresses Zy in different points

Table 9. Results of stresses Zz•in different points and radiuses

In these tables the coincidence of one or two figures is observed. Further consider the problems for prismatic body of quadratic section with rectangular quadratic cavity, where rounded character of internal and external angles are considered with radiuses r1=0.03≈(); r2=0.05≈(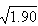); r3=0.1≈(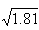); r4=0.2≈(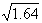); r1⁽²⁾=0.003≈(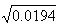); r2⁽²⁾=0.005≈(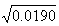); r3⁽²⁾=0.001≈()

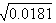In this case an equation of boundary is determined by the following way: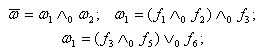

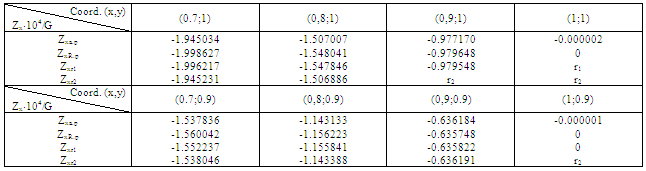
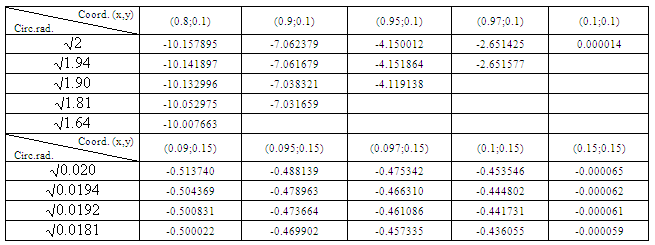
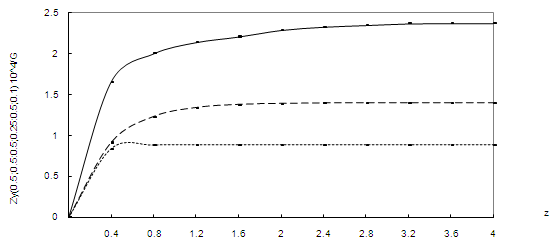
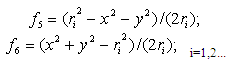To study the effect of external and internal angle points on the behavior of stress state of prismatic bodies with arbitrary forms of cavity the body with rounded angles with different radiuses of external and internal quadrate was considered. Results of study of stresses Z_z•10⁴/G are given in Table 9 with initial data obtained earlier.

As seen from the Table rounded character of external angle effects less than rounded character of internal angle, that is cavity.

5. Conclusions

Therefore, on the base of above given calculations, we can assert, that the R − function procedures can be used for calculations of prismatic bodies of any section with any cavity configuration.

So we may state that worked out algorithm on the basis of the method of successive approximations and R-functions may be applied to the solution of practical problems of constraint torsion in prismatic domains of arbitrary section with different forms of cavities or inclusions, as well as side depressions; here methodology permits to use different hypothesis to determine the angle of torsion.

The paper presents the results of computational experiment and investigations, connected with design of practically necessary elements of structure of the type of prismatic bodies of arbitrary section with different form of cavity.