-
Paper Information
- Next Paper
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Computational and Applied Mathematics
2012; 2(4): 166-173
doi: 10.5923/j.ajcam.20120204.05
Generalised Differential Quadrature Method in the Study of Free Vibration Analysis of Monoclinic Rectangular Plates
Prag Singhal , Garima Bindal
Department of Applied Sciences and Humanities, ABES Engineering College, Ghaziabad
Correspondence to: Prag Singhal , Department of Applied Sciences and Humanities, ABES Engineering College, Ghaziabad.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Vibration characteristics of monoclinic rectangular plate of exponentially varying thickness resting on elastic foundation have been studied on the basis of classical plate theory. Following Lévy approach i.e. two parallel edges (y = 0 and b) are assumed to be simply-supported while the other two edges (x = 0 and a) may have either of three combinations C-C, C-S or C-F, where C, S and F stand for clamped, simply supported and free edge, respectively. Assuming the transverse displacement w to vary as sin (pπy/b), the partial differential equation which governs the motion of equation is reduced to an ordinary differential equation in x with variable coefficients. The resulting ordinary differential equation has been solved by Generalised Differential Quadrature Method (GDQM) for all the boundary conditions considered here. The effect of various plate parameters has been studied on the natural frequencies for the first three modes of vibration. Convergence studies have been carried out for four decimal exactitude. Mode shapes for all the three plates have been presented. The efficiency of generalized differential quadrature method for the natural frequencies of vibration of monoclinic rectangular plates has been examined.
Keywords: GDQM, Monoclinic Material, Vibrations, Winkler Foundation
Article Outline
1. Introduction
- Free vibration analysis of plate structure is one of the main vital tasks for an engineer to accomplish in the engineering design. Such type of free vibration problems are generally described by a linear partial differential equation associated with a set of related boundary conditions, whose closed form solution is not possible. As a result, the various numerical methods such as the finite difference method[1], Galerkin’s method[2],Rayleigh-Ritz method[3],quintic splines method[4], finite-element method[5], Chebyshev collocation method[6], and Differential quadrature method[7-10] have been employed to study the vibrational characteristics of plates of various geometries.Differential quadrature method (DQM) is a collocation scheme and was first introduced by Bellman et al.[11]. Malik and Civan[12] have presented comprehensive results showing that the DQM stands out in numerical accuracy as well as computational efficiency over the finite difference and finite element methods. The application of DQM covers almost all the areas of structural and vibration analysis of shells, beams and plates etc. The DQM is used to determine the weighting coefficients for the first order derivative approximation, in which the derivative of a function with respect to a spatial variable at a given discrete point can be expressed as a weighted linear sum of the function values at all the discrete points in the computational domain. Bellman et al.[13] proposed two methods to compute the weighting coefficients. In the first method, weighting coefficients are determined by solving a system of algebraic equations, in which the coordinate of the grid points to be chosen arbitrary. But, in this method, it is very difficult to obtain the weighting coefficients for a large number of grid points as it results to an ill-conditioned matrix since the corresponding differential matrix becomes increasingly large [14]. In the second method, the weighting coefficients are determined by a simple algebraic formula and the grid points are chosen as the roots of shifted Legendre polynomial. Shu et al.[15] proposed the generalized differential quadrature (GDQ) method in which Lagrange interpolation polynomial is used as the basis function. An algebraic expression is presented to compute the weighting coefficients of the first order derivative approximation and the recurrence formula is used to compute the weighting coefficients for higher order derivatives without restriction on the choice of the grid points.The advantages of the GDQ method included no restriction on the number of grid points used for the approximation and the weighted coefficients are determined using simple recurrence relation instead of solving a set of linear algebraic equations as in other version of differential quadrature method. A more in depth analysis of the merits of the GDQ method can be found in Du. et al.[16]. Recently, the GDQ method has been applied to solve fluid dynamics and buckling of composite structure problems [17,18].The plates of variable thickness have significantly greater efficiency for vibration as compared to the plates of uniform thickness and also provide the advantage of reduction in weight and size. Notable contribution made thereafter dealing with rectangular plates with uniform / non-uniform thickness with various boundary conditions are given in the refs. [19-23].The analysis of structures on elastic foundations is of considerable interest and widely used in several engineering fields, such as foundation, pavement and railroad, pipeline and some aero-space structures applications. The different foundation models (Vlasov, Winkler and Pasternak etc.) have been proposed in the literature [24] to approximate the foundation characteristics. Numerous studies dealing with Winkler foundation are available in the literature and are reported in the refs. [25, 26].The free vibration analysis of homogeneous monoclinic rectangular plates with exponentially varying thickness resting on Winkler foundation has been solved by Generalized Differential Quadrature method (GDQM). Frequencies and mode shapes for different boundary conditions (C-C, C-S and C-F) for the first three modes of vibration are computed. The present work and the results may be an orientation to the future research work.
2. Mathematical Formulation
- Consider a rectangular monoclinic plate of length a, breadth b, thickness h, density ρ and resting on a Winkler-type foundation with foundation modulus kf referred to rectangular Cartesian co-ordinates system. The differential equation governing the free transverse vibration of monoclinic rectangular plate is given by
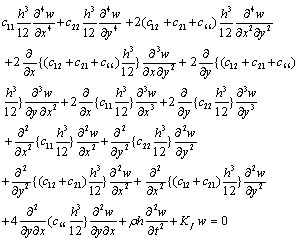 | (1) |
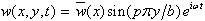 | (2) |
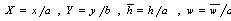 The equation (1) reduces to
The equation (1) reduces to 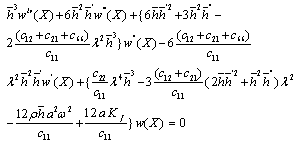 | (3) |
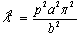 and primes denote the differentiation w.r.t. ‘X’.We assume that the thickness and density of the plate are varying exponentially along the X-direction and are given by
and primes denote the differentiation w.r.t. ‘X’.We assume that the thickness and density of the plate are varying exponentially along the X-direction and are given by 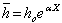 and
and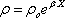 , where
, where 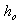 and
and 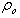 are the thickness and density of the plate respectively at the end X=0, α and β are the taper and density parameters respectively.With these notations, equation (3) reduces to
are the thickness and density of the plate respectively at the end X=0, α and β are the taper and density parameters respectively.With these notations, equation (3) reduces to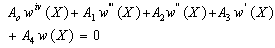 | (4) |
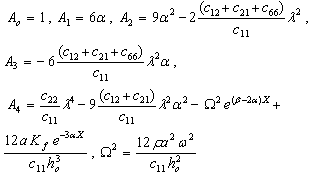 The solution of equation (4) together with the boundary conditions at the edges X = 0 and X = 1 gives rise to a two-point boundary value problem with variable coefficients whose closed form solution is not possible. An approximate solution is obtained by employing generalised differential quadrature method.
The solution of equation (4) together with the boundary conditions at the edges X = 0 and X = 1 gives rise to a two-point boundary value problem with variable coefficients whose closed form solution is not possible. An approximate solution is obtained by employing generalised differential quadrature method.3. Method of solution: Generalised Differential Quadrature Method
- The GDQ approximates a partial derivative of a function with respect to a variable at any discrete point as a weighted sum of the function values at all the discrete points chosen in the overall domain of that variable and approximates continuous function with a higher-order polynomial in the overall variable domain. The nth order derivative of W(X) w.r.t. X can be expressed discretely at the point Xi as
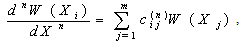 | (5) |
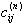 are the weighting coefficients associated with the nth order derivative of W(X) w. r. t. X at discrete point Xi. In the generalized differential quadrature (GDQ) method [16, 17], the global Lagrange interpolation polynomial is used as the test function
are the weighting coefficients associated with the nth order derivative of W(X) w. r. t. X at discrete point Xi. In the generalized differential quadrature (GDQ) method [16, 17], the global Lagrange interpolation polynomial is used as the test function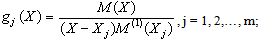 | (6) |
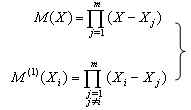 | (7) |
 is the first derivative of M(X). Thus, the weighting coefficients
is the first derivative of M(X). Thus, the weighting coefficients 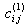 (i, j = 1, 2,…, m) can be obtained analytically from the differentiation of equation (6) to obtain
(i, j = 1, 2,…, m) can be obtained analytically from the differentiation of equation (6) to obtain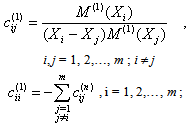 | (8) |
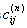 .
.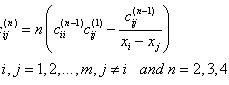 | (9) |
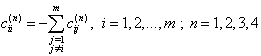 | (10) |
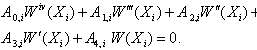 | (11) |
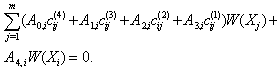 | (12) |
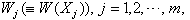 which can be written in the matrix form as
which can be written in the matrix form as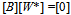 | (13) |
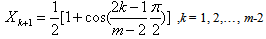 | (14) |
4. Boundary Conditions and Frequency Equations
- The three different combinations of boundary conditions namely, C-C, C-S and C-F have been considered here, where C, S, F stand for clamped, simply supported and free edge, respectively and first symbol denotes the condition at the edge X=0 and second symbol at the edge X=1.By satisfying the relations
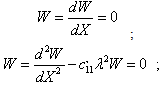 and
and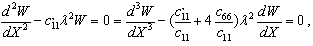 where
where 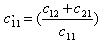 for clamped, simply supported and free edge conditions, respectively, a set of four homogeneous equations in terms of unknown Wj are obtained. These equations together with field equation (13) give a complete set of m homogeneous equations in m unknowns. For C-C plate this set of equations can be written as
for clamped, simply supported and free edge conditions, respectively, a set of four homogeneous equations in terms of unknown Wj are obtained. These equations together with field equation (13) give a complete set of m homogeneous equations in m unknowns. For C-C plate this set of equations can be written as 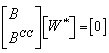 | (15) |
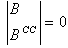 | (16) |
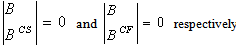 | (17,18) |
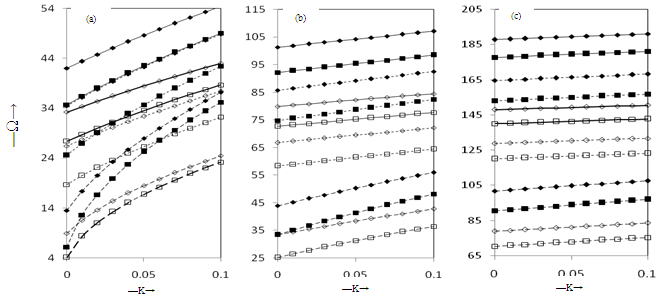
5. Numerical Results and Discussion
- The frequency equations (16-18) have been solved numerically to compute the values of the frequency parameter Ω for various values of plate parameters. The effect of foundation parameter, density parameter, taper parameter and aspect ratio on frequency parameter Ω has been analysed for C-C, C-S and C-F plates vibrating in first three modes of vibration. The elastic constants for the plate material (rock gypsum)[Haussuhl] are taken as
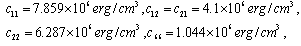 given by Haussuhl,1965 (rock gypsum) as monoclinic material. This is obtained by taking p = 1 and thickness
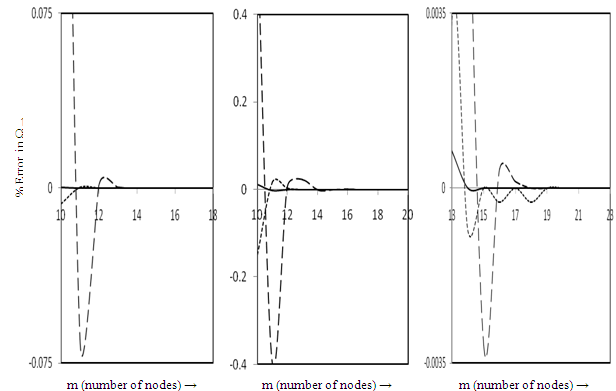
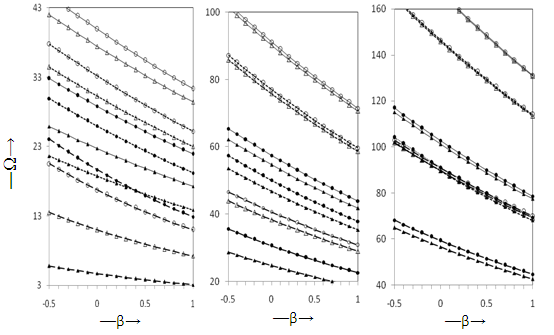
given by Haussuhl,1965 (rock gypsum) as monoclinic material. This is obtained by taking p = 1 and thickness 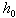 = 0.1 at the edge X = 0. To choose the appropriate number of collocation points m, convergence studies have been carried out for various sets of parameters for all the three plates. Convergence graphs are shown in the figures 1(a-c) for a/b = 1.0, K = 0.02, α = 0.5 and β = 0.5 for C-C, C-S and C-F plates respectively. For these data the maximum deviation were observed. In all the computations, m = 20 has been fixed for all the boundary conditions in the first three modes since further increase in m does not improve the results even in the fourth place of decimal.The behaviour of frequency parameter Ω with density parameter β for the first mode of vibration for C-C, C-S and C-F plates for two different values of foundation parameter K = 0.0, 0.02, taper parameter α = -0.5, 0.5 and aspect ratio a/b = 1 is shown in figure 2(a). It is found that the frequency parameter Ω decreases with increasing values of density parameter β keeping other plate parameters fixed. The rate of decrease in frequency parameter Ω with β increases with the increase in the values of foundation parameter K and taper parameter α. This rate of decrease is higher in the order C-C > C-S > C-F plates. A similar behavior is observed for the second and third modes of vibration as shown in figures 2(b) and 2(c). The rate of decrease in Ω with β is higher in third mode as compared to second and first modes for all the plates.
= 0.1 at the edge X = 0. To choose the appropriate number of collocation points m, convergence studies have been carried out for various sets of parameters for all the three plates. Convergence graphs are shown in the figures 1(a-c) for a/b = 1.0, K = 0.02, α = 0.5 and β = 0.5 for C-C, C-S and C-F plates respectively. For these data the maximum deviation were observed. In all the computations, m = 20 has been fixed for all the boundary conditions in the first three modes since further increase in m does not improve the results even in the fourth place of decimal.The behaviour of frequency parameter Ω with density parameter β for the first mode of vibration for C-C, C-S and C-F plates for two different values of foundation parameter K = 0.0, 0.02, taper parameter α = -0.5, 0.5 and aspect ratio a/b = 1 is shown in figure 2(a). It is found that the frequency parameter Ω decreases with increasing values of density parameter β keeping other plate parameters fixed. The rate of decrease in frequency parameter Ω with β increases with the increase in the values of foundation parameter K and taper parameter α. This rate of decrease is higher in the order C-C > C-S > C-F plates. A similar behavior is observed for the second and third modes of vibration as shown in figures 2(b) and 2(c). The rate of decrease in Ω with β is higher in third mode as compared to second and first modes for all the plates.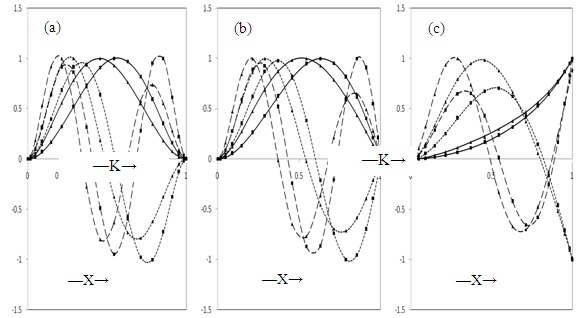 | Figure 6. Normal displacements: (a) C-C plate, (b) C-S plate, (c) C-C plate, for a/b = 1.0, β = 0.5, K = 0.02, , first mode; -------- , second mode; – – – –, third mode; ■, α = -0.5; ▲, α = 0.5 |
6. Conclusions
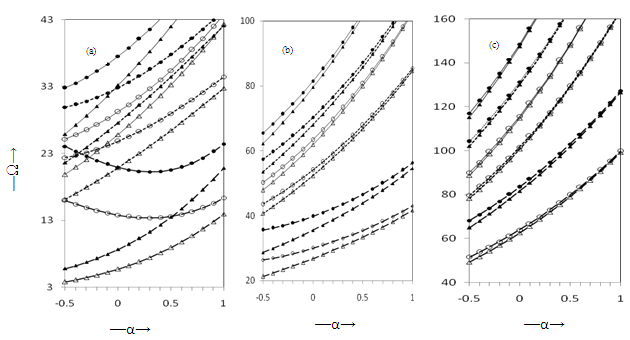
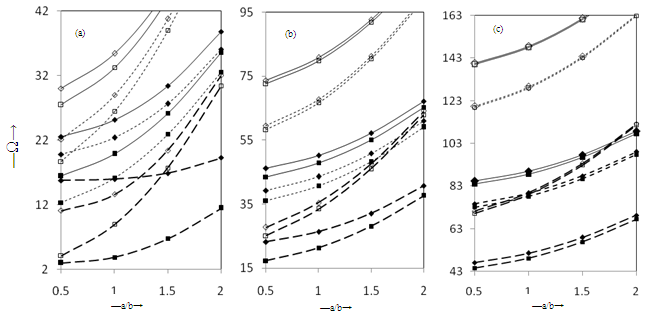
- The effects of Winkler foundation on natural frequencies of rectangular plates composed by a monoclinic material with exponentially varying thickness have been studied on the basis of classical plate theory. It is observed that frequency parameter Ω increases with the increase in foundation parameter K and aspect ratio a/b while decreases with the increasing value of density parameter β keeping all other plate parameters fixed for all the three boundary conditions. However, the behaviour with taper parameter α is not monotonous. The implementation of the GDQ method is relatively easier and the efforts needed for solving the problem with GDQM is also relatively less in comparison to the other numerical methods. The limitations of the proposed method are that the accuracy does not meet in case of complicated geometries.The present study is of great significance to design engineers in obtaining the desired frequency by a proper choice of one or more parameters considered here.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML