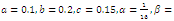-
Paper Information
- Next Paper
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Computational and Applied Mathematics
2012; 2(4): 159-165
doi: 10.5923/j.ajcam.20120204.04
The Existence of at most Twenty Seven Nonnegative Equilibrium Points in a Class of 3-D Competitive Cubic Systems
Helmar Nunes Moreira
Department of Mathematics, University of Brasília, Brasília-DF, CEP70910-900, Brazil
Correspondence to: Helmar Nunes Moreira , Department of Mathematics, University of Brasília, Brasília-DF, CEP70910-900, Brazil.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
This paper presents the stability analysis of equilibrium points of a model involving competition between three species subject to a strong Allee effect which occurs at low population density. By using the software of MAPLE 10, we prove that, under certain conditions, the model has at most twenty seven nonnegative equilibrium points and, via Lyapunov function, we derive criteria for the asymptotical stability of the unique positive equilibrium point.
Keywords: Allee Effect, Competition Model Of Three Species, Lyapunov Theorem
Article Outline
1. Introduction
- The Allee model of growth has been widely and successfully used as a simple, yet adequate descriptor of the dynamics of small populations or critical depensation model[1], and many theoretical studies (e.g.[2],[3]) have been achieved. The Allee effect refers to reduced fitness or decline in population growth at low population densities. In population models, the Allee effect is often modeled as a threshold, below which there is population extinction.In the present paper, we consider the Allee effect within the context of the symmetric model of three competing species. We wish to point out that an model of two competing species with Allee effect was proposed and studied in[2-4], and some papers dealing with experiments, simulations, or combinations of these competitive systems among others are described in[5-6]. In Section 2, we introduce the symmetric model of three competing species subject to the Allee effects. The main analytical results on stability analysis of the equilibrium points, are presented in Section 3. Section 4 is devoted to a discussion, in the context of numerical simulation, of the analytical results obtained in this paper. Concluding remarks on the paper are made at the end.
2. A three-species Competitive System Subject to the Allee Effects
- In the three-species Lotka-Volterra competition models (e.g.[7-11]), it is possible for one- or two species extinction, or global stability of a positive three-species equilibrium, periodic solutions or a stable heteroclinic orbit (e.g.[12-14]). Here, we shall propose a new three-competitive model that specifically predicts Allee growth of speciesx,y, and z, respectively. Keeping this in mind, the model is described as follows:
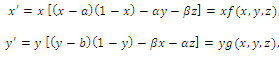 | (2.1) |
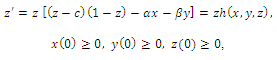 ,where
,where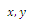 and z are the population densities,
and z are the population densities, 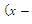
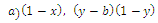 and
and 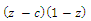 are the quadratic intrinsic growth rates at intermediate densities,
are the quadratic intrinsic growth rates at intermediate densities, 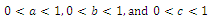 are the lower threshold of the population densities
are the lower threshold of the population densities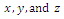 , respectively,
, respectively, 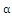 and
and 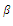 are the coefficients of interspecies competition, and (‘=
are the coefficients of interspecies competition, and (‘=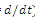 . Throughout this paper we assume that
. Throughout this paper we assume that 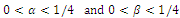 .In our model we consider that the intrinsic growth rates are quadratic and we prove that, under certain conditions, system (2.1) has at most twenty seven nonnegative equilibria. By using the software of MAPLE 10, a numerical example is provided to illustrate the behavior of the system (2.1) for a biologically reasonable range of parameters with only one asymptotically stable equilibrium point and seven unstable equilibrium points in
.In our model we consider that the intrinsic growth rates are quadratic and we prove that, under certain conditions, system (2.1) has at most twenty seven nonnegative equilibria. By using the software of MAPLE 10, a numerical example is provided to illustrate the behavior of the system (2.1) for a biologically reasonable range of parameters with only one asymptotically stable equilibrium point and seven unstable equilibrium points in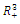 . We believe that this is the first time that the three-species competition system (2.1) has been formulated and analyzed in the literature.
. We believe that this is the first time that the three-species competition system (2.1) has been formulated and analyzed in the literature.2.1. Boundedness of the Solutions
- Consider the system (2.1). Obviously the functions
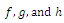 are continuous and Lipschitzian with respect to all independent variables on
are continuous and Lipschitzian with respect to all independent variables on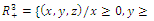
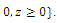 . Therefore, a solution of the system (2.1) with nonnegative initial conditions exists and is unique. The basic existence and uniqueness theorem for differential equations ensures thatLemma 2.1. The positive cone Int
. Therefore, a solution of the system (2.1) with nonnegative initial conditions exists and is unique. The basic existence and uniqueness theorem for differential equations ensures thatLemma 2.1. The positive cone Int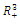 is invariant for system (2.1).Lemma 2.2. The solutions
is invariant for system (2.1).Lemma 2.2. The solutions 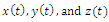 of system (2.1) with positive initial conditions are bounded for all
of system (2.1) with positive initial conditions are bounded for all 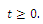 Proof. Since
Proof. Since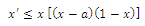 , then
, then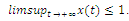 . Here, we consider the case of strong Allee effect :
. Here, we consider the case of strong Allee effect :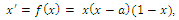 ),where
),where 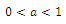 is the survival threshold. There are three equilibrium points
is the survival threshold. There are three equilibrium points 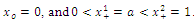 . The relative extrema of the function
. The relative extrema of the function 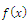 are
are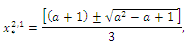 which give the points of inflection of the graph of
which give the points of inflection of the graph of 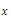 versus t. The solutions are increasing and concave down when
versus t. The solutions are increasing and concave down when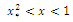 ; increasing and concave up when
; increasing and concave up when 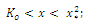 decreasing and concave down when
decreasing and concave down when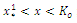 ; decreasing and concave up when
; decreasing and concave up when 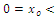
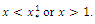 .We conclude that
.We conclude that 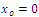 and
and 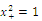 are sinks; and
are sinks; and 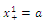 is a source. Then if the initial population size is below a , the population
is a source. Then if the initial population size is below a , the population 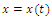 will die out.Similarly to
will die out.Similarly to 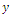 and z , respectively.
and z , respectively.3. Existence and Stability of Equilibrium Points
- Computations of the boundary equilibria and the analysis of the existence of positive equilibrium points and their stability for system (2.1), provide the information needed to determine the coexistence or extinction of species. To do so, we compute the Jacobian matrix
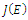 of (2.1). The signs of the real parts of the eigenvalues of
of (2.1). The signs of the real parts of the eigenvalues of 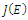 evaluated at a given equilibrium point
evaluated at a given equilibrium point 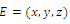 determine its stability. Here
determine its stability. Here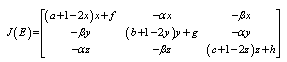 | (3.1) |
 e are as in (2.1),
e are as in (2.1), 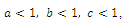 ,
, 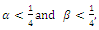 and all the parameters are positive. System (2.1) has at most twenty seven non-negative equilibria:
and all the parameters are positive. System (2.1) has at most twenty seven non-negative equilibria: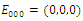 , with eigenvalues
, with eigenvalues 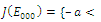
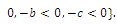 Thus,
Thus, 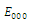 is locally asymptotically stable;
is locally asymptotically stable;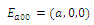 , with eigenvalues
, with eigenvalues 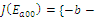
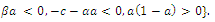 .This implies that
.This implies that 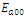 is unstable;
is unstable;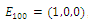 , where eigenvalues
, where eigenvalues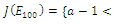
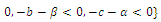 . Thus,
. Thus, 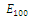 is locally asymptotically stable;
is locally asymptotically stable;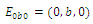 , where eigenvalues
, where eigenvalues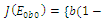
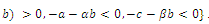 . This implies that
. This implies that 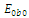 is unstable;
is unstable;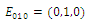 , with eigenvalues
, with eigenvalues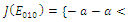
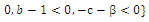 . Thus,
. Thus, 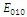 is locally asymptotically stable;
is locally asymptotically stable;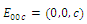 , where eigenvalues
, where eigenvalues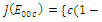
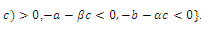 ,. This implies that
,. This implies that 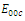 is unstable;
is unstable;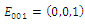 with eigenvalues
with eigenvalues 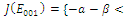
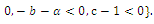 Thus
Thus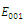 is locally asymptotically stable;Now we establish criteria for the existence and stability of the equilibrium
is locally asymptotically stable;Now we establish criteria for the existence and stability of the equilibrium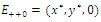 . For this case, one of the three competitors goes to extinction depending on the initial values and the coexistence of three competing species described by (2.1) is not possible. Thus the exclusion principle holds[10]. When system (2.1) is restricted to
. For this case, one of the three competitors goes to extinction depending on the initial values and the coexistence of three competing species described by (2.1) is not possible. Thus the exclusion principle holds[10]. When system (2.1) is restricted to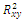 , we obtain the following subsystem:
, we obtain the following subsystem: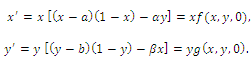 | (3.2) |
 occurring in the
occurring in the 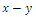 plane exists if and only if the algebraic system
plane exists if and only if the algebraic system 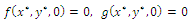 has a positive solution. A routine computation yields
has a positive solution. A routine computation yields 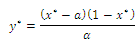 and
and 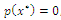 where
where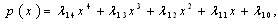 | (3.3) |
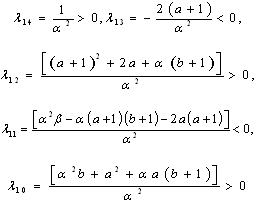 Using the rule of signs of Descartes it follows: (a) There are four sign changes in
Using the rule of signs of Descartes it follows: (a) There are four sign changes in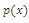 , so there are 4, 2 or 0 positive roots; (b) There are no sign changes at
, so there are 4, 2 or 0 positive roots; (b) There are no sign changes at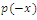 , so there are no negative roots. Hence, at most four positive equilibrium points are possible in the
, so there are no negative roots. Hence, at most four positive equilibrium points are possible in the 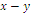 plane[15].Under certain conditions on the parameters we have the following geometric interpretation (see Fig.3.1):Proposition 3.1. Let
plane[15].Under certain conditions on the parameters we have the following geometric interpretation (see Fig.3.1):Proposition 3.1. Let 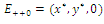 denote an interior equilibrium in the
denote an interior equilibrium in the 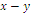 plane. Then
plane. Then 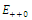 is the intersection of ellipses
is the intersection of ellipses 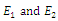 defined by
defined by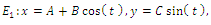 | (3.4) |
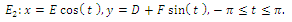 where
where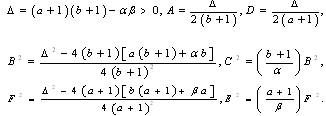 Proposition 3.2. Consider the system (2.1). Suppose that there are four interior equilibria
Proposition 3.2. Consider the system (2.1). Suppose that there are four interior equilibria 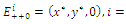
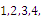 in the
in the 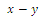 plane; that is,
plane; that is, 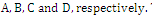 Then only one equilibrium c of coexisting populations is locally stable and its basin of attraction is bounded by the stable separatrices of the saddle B s and D , both coming from the unstable node A.
Then only one equilibrium c of coexisting populations is locally stable and its basin of attraction is bounded by the stable separatrices of the saddle B s and D , both coming from the unstable node A.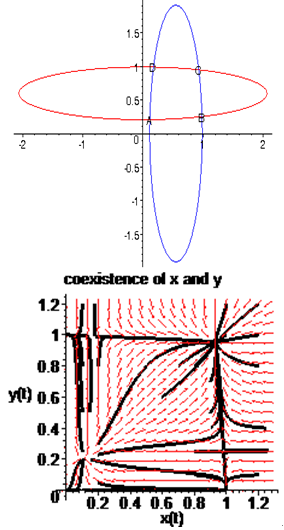 | Figure 3.1. Intersection between two ellipses . The equilibrium points are: . The equilibrium points are:  is an unstable node; is an unstable node; 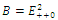 is a saddle point; is a saddle point; 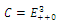 is locally asymptotically stable; is locally asymptotically stable; 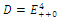 is a saddle point. Here is a saddle point. Here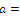 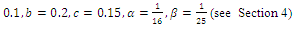 |
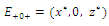 and
and 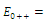
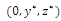 are obtained from (2.1).
are obtained from (2.1).3.1. Existence, Stability and Linearization of Positive Equilibrium Points
- Let
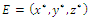 denote an interior equilibrium point of
denote an interior equilibrium point of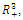 , if it exists. It follows from direct substitution and algebraic manipulation:Proposition 3.3. System (2.1) has at most eight equilibrium points in the interior of
, if it exists. It follows from direct substitution and algebraic manipulation:Proposition 3.3. System (2.1) has at most eight equilibrium points in the interior of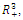 . Their equilibrium values
. Their equilibrium values 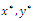 and
and 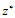 are given by
are given by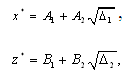 and
and 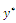 is a positive root of
is a positive root of 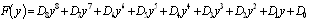 | (3.5) |
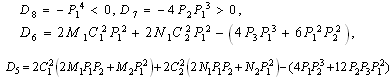 ,
,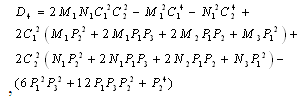
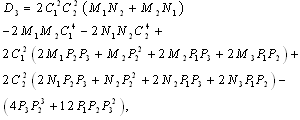
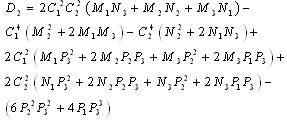
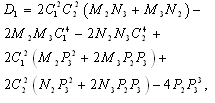
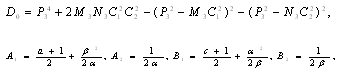
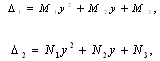
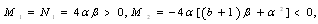
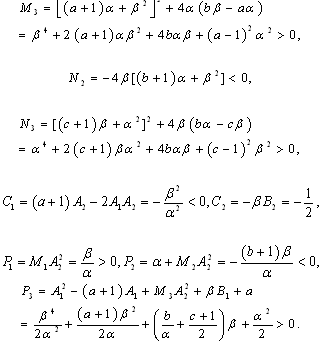 Corollary 3.1. Suppose that
Corollary 3.1. Suppose that 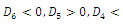
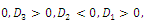 and
and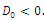 Then
Then 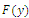 has 8, 6, 4, 2 or 0 positive roots.Corollary 3.2. Suppose
has 8, 6, 4, 2 or 0 positive roots.Corollary 3.2. Suppose 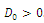 Then
Then 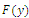 has at least one positive root.Proof. Clearly,
has at least one positive root.Proof. Clearly, 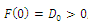 and
and 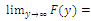
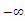 Hence, there exists a
Hence, there exists a 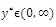 so that
so that 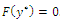 This completes the proof. Remark 3.1 Using the software MAPLE, we obtain the following numerical examples:(i)
This completes the proof. Remark 3.1 Using the software MAPLE, we obtain the following numerical examples:(i) 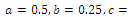
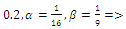 none positive equilibrium; (ii)
none positive equilibrium; (ii) 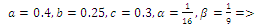 two positive equilibriums with eigenvalues (-,+,+),(+,+,+); (iii)
two positive equilibriums with eigenvalues (-,+,+),(+,+,+); (iii) 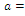
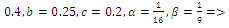 two positive equilibriums with eigenvalues (-,+,+),(+,α
two positive equilibriums with eigenvalues (-,+,+),(+,α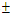 iβ), α
iβ), α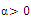 ; (iv)
; (iv) 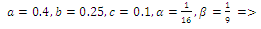 four positive equilibriums with eigenvalues (+,+,+),(+,-,+),(-,-,+),(-,+,+).It is always informative to draw the set of positive equilibrium points of the system (2.1) in
four positive equilibriums with eigenvalues (+,+,+),(+,-,+),(-,-,+),(-,+,+).It is always informative to draw the set of positive equilibrium points of the system (2.1) in 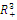 Here the set is defined by the intersection of the surfaces:
Here the set is defined by the intersection of the surfaces: 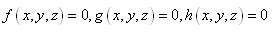 | (3.6) |
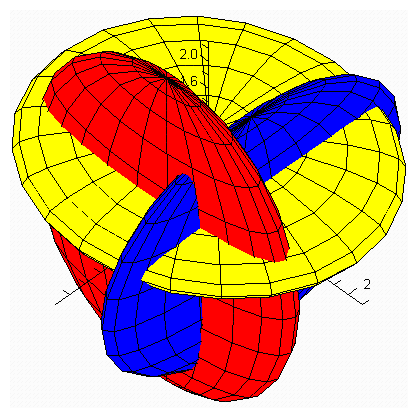 | Figure 3.2. Intersection between ellipsoids 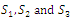 There are 8 equilibrium points in There are 8 equilibrium points in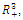 . Here . Here 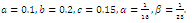 |
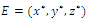 denote the interior equilibrium of the system (2.1), if it exists. Then E is the intersection of three ellipsoids
denote the interior equilibrium of the system (2.1), if it exists. Then E is the intersection of three ellipsoids 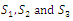 :
: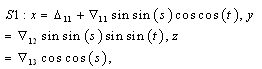
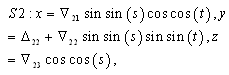
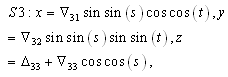
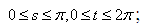 ;
;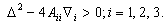 | (3.7) |
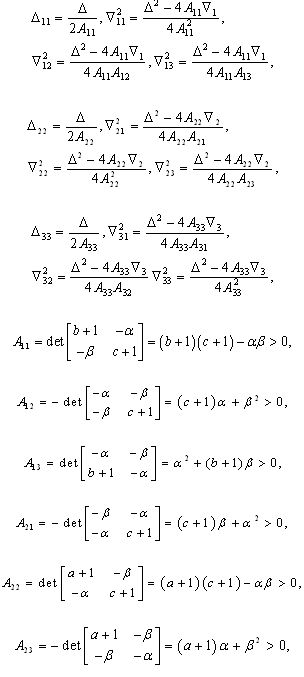
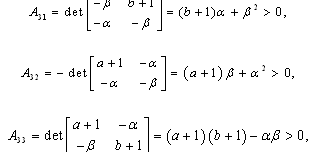
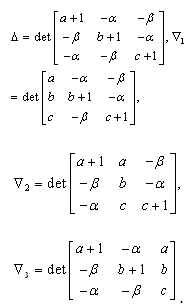 .To determine the stability of a positive equilibrium point of (2.1), we will use the direct method of Lyapunov:
.To determine the stability of a positive equilibrium point of (2.1), we will use the direct method of Lyapunov:3.2. Direct Method of Lyapunov
- Next let us consider the local stability of a positive equilibrium pointє
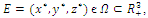 , where
, where 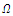 is a neighborhood of
is a neighborhood of 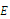 to be determined. Based on the “direct method” of Lyapunov, we construct a continuous function
to be determined. Based on the “direct method” of Lyapunov, we construct a continuous function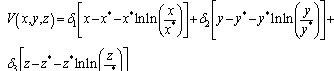 | (3.8) |
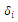 (i=1,2,3) are positive constant numbers which are yet unspecified, satisfying the following properties:
(i=1,2,3) are positive constant numbers which are yet unspecified, satisfying the following properties: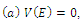 ,(b)
,(b) 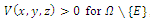 , that is, the equilibrium point E is an isolated minimum of
, that is, the equilibrium point E is an isolated minimum of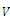 . In fact,
. In fact,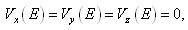
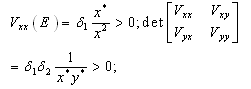
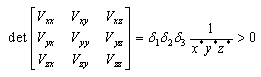 where the partial derivatives are calculated at
where the partial derivatives are calculated at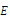 . (c) The function
. (c) The function 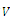 is continuously differentiable on the neighborhood
is continuously differentiable on the neighborhood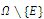 , and, on this set,
, and, on this set, 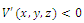 . Here,
. Here,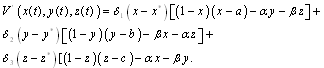 Since,
Since, 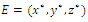 is a positive equilibrium point of system (2.1),
is a positive equilibrium point of system (2.1), 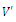 satisfies
satisfies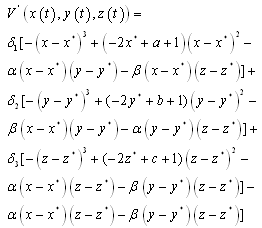 | (3.9) |
 is an isolated maximum of
is an isolated maximum of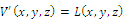 , then (c) follows easily, that is:(c1) We note that E is a critical point of the function
, then (c) follows easily, that is:(c1) We note that E is a critical point of the function 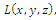 that is
that is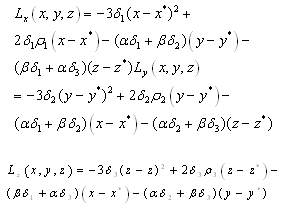 implies
implies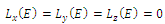 . (c2) The equilibrium point E is a maximum point of
. (c2) The equilibrium point E is a maximum point of 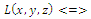
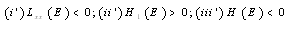 | (3.10) |
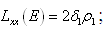
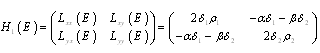 ;
;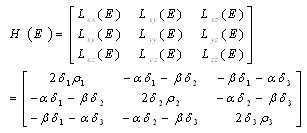 Letting
Letting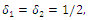 we can rewrite (3.10) as
we can rewrite (3.10) as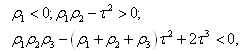
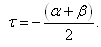 | (3.11) |
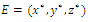 is a isolated maximum of
is a isolated maximum of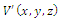 , i.e., there is a neighborhood
, i.e., there is a neighborhood 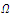 of
of 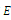 such that
such that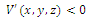 , on this set . The pertinent result, which we prove, is the following (see Fig.3.3):.Proposition 3.5. Consider the Lyapunov function (3.8) defined in the neighborhood
, on this set . The pertinent result, which we prove, is the following (see Fig.3.3):.Proposition 3.5. Consider the Lyapunov function (3.8) defined in the neighborhood 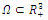 of a positive equilibrium point E of the competitive system (2.1). If (3.11) occurs, then
of a positive equilibrium point E of the competitive system (2.1). If (3.11) occurs, then 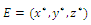 is locally asymptotically stable .
is locally asymptotically stable .4. Numerical example
- By using the software of MAPLE 10, a numerical example has been provided to illustrate the behavior of the system (2.1) for a biologically reasonable range of parameters. Choosing the following set of values for the parameters in (2.1):
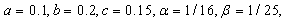 we find that the inequalities given by (3.11) hold for a unique positive equilibrium point and we observe that there are 27 equilibrium points given by
we find that the inequalities given by (3.11) hold for a unique positive equilibrium point and we observe that there are 27 equilibrium points given by
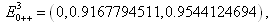 ,
,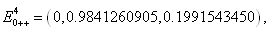
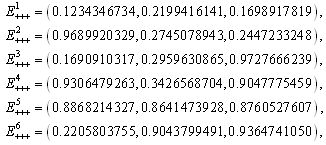
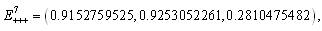
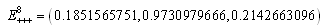 The
The  of the positive equilibrium points
of the positive equilibrium points 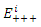 (i=1…8) are roots of (3.5), that is
(i=1…8) are roots of (3.5), that is , where
, where In the equilibrium point
In the equilibrium point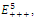 , the characteristic equation (4.11) of
, the characteristic equation (4.11) of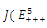 ) reduces to
) reduces to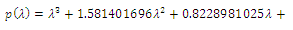
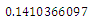 , with roots
, with roots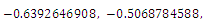
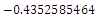 . This implies that
. This implies that 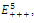 is a locally asymptotically stable equilibrium point. Here, we observe that the equilibrium points
is a locally asymptotically stable equilibrium point. Here, we observe that the equilibrium points 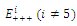 are unstable.In the absence of a competitor, we have: (a)
are unstable.In the absence of a competitor, we have: (a) 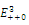 is a locally asymptotically stable equilibrium point, with eigenvalues -0.7346114284, -0.6340454548 and -0.2460382656. The equilibrium points
is a locally asymptotically stable equilibrium point, with eigenvalues -0.7346114284, -0.6340454548 and -0.2460382656. The equilibrium points 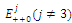 are unstable. (b)
are unstable. (b)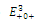 is a locally asymptotically stable equilibrium point, with eigenvalues -0.7933441170, -0.6268358235, -0.2959390916. The equilibrium points
is a locally asymptotically stable equilibrium point, with eigenvalues -0.7933441170, -0.6268358235, -0.2959390916. The equilibrium points 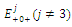 are unstable. (c)
are unstable. (c)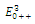 is a locally asymptotically stable equilibrium point, with eigenvalues -0.7381379376, -0.5669278285, -0.1954752145. The equilibrium points
is a locally asymptotically stable equilibrium point, with eigenvalues -0.7381379376, -0.5669278285, -0.1954752145. The equilibrium points 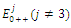 are unstable.In the absence of two competitors, we have: (d)
are unstable.In the absence of two competitors, we have: (d) 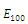 is a locally asymptotically stable equilibrium point, with eigenvalues
is a locally asymptotically stable equilibrium point, with eigenvalues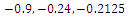 . The equilibrium
. The equilibrium 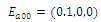 is unstable. (e)
is unstable. (e) 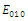 is a locally asymptotically stable equilibrium point, with eigenvalues
is a locally asymptotically stable equilibrium point, with eigenvalues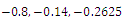 . The equilibrium
. The equilibrium 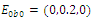 is unstable. (f)
is unstable. (f) 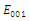 is a locally asymptotically stable equilibrium point, with eigenvalues
is a locally asymptotically stable equilibrium point, with eigenvalues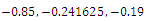 . The equilibrium
. The equilibrium 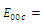
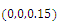 is unstable.Clearly
is unstable.Clearly 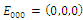 is a locally asymptotically stable equilibrium point, with eigenvalues -0.1, -0.2, -0.15, respectively. The
is a locally asymptotically stable equilibrium point, with eigenvalues -0.1, -0.2, -0.15, respectively. The 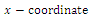 of the equilibrium points
of the equilibrium points 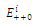 (i=1…4) are roots of (3.3)
(i=1…4) are roots of (3.3) 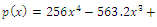
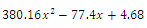 . Intersection between two ellipses:
. Intersection between two ellipses: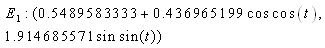
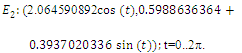 The
The  of the equilibrium points.
of the equilibrium points. 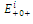 (i=1…4) are roots of
(i=1…4) are roots of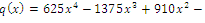
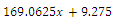 . Intersection between two ellipses:
. Intersection between two ellipses: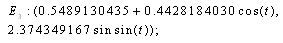
 The equilibrium points are:
The equilibrium points are: 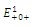 is an unstable node;
is an unstable node; 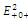 is a saddle point;
is a saddle point; 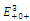 is locally asymptotically stable;
is locally asymptotically stable; 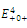 is a saddle point.The
is a saddle point.The 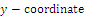 of the equilibrium points
of the equilibrium points 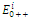 (i=1…4) are roots of the polynomial
(i=1…4) are roots of the polynomial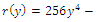
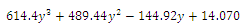 :. Intersection between two ellipses:
:. Intersection between two ellipses: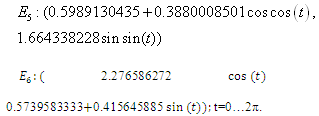 The equilibrium points are:
The equilibrium points are: 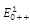 is an unstable node;
is an unstable node; 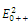 is a saddle point;
is a saddle point; 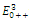 is locally asymptotically stable;
is locally asymptotically stable; 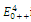 is a saddle point.
is a saddle point.5. Concluding Remarks
- In this paper, a mathematical model of competition between three populations with lower threshold sizes has been proposed and investigated. The main focus was to analyze the question of existence and stability of nonnegative equilibria. Our results show that there exist at most twenty-seven equilibrium points for the system under consideration and, by using the software of MAPLE 10, a numerical example has been provided to illustrate the behavior of the system (2.1) for a biologically reasonable range of parameters with only one positive equilibrium asymptotically stable and 7 positive unstable equilibrium points.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML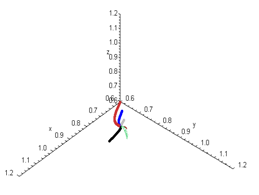
 population evolution in the state space for system
population evolution in the state space for system . The initial conditions are (0,0,0),(0.9,0.9,0.9),(0.8,0.8,0.8),(0.7,0.7,0.7),(0.6,0.6,0.6),(1.0,0.9,0.9).The equilibrium point
. The initial conditions are (0,0,0),(0.9,0.9,0.9),(0.8,0.8,0.8),(0.7,0.7,0.7),(0.6,0.6,0.6),(1.0,0.9,0.9).The equilibrium point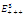 is locally asymptotically stable. Here
is locally asymptotically stable. Here 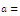
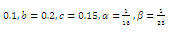
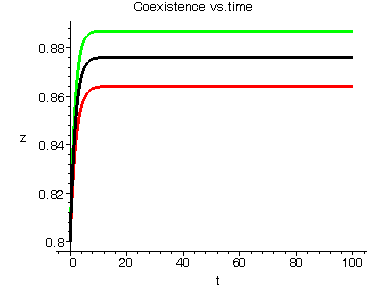
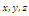 population changes with respect to time for system (2.1). Each trajectory starts at a point (0.8,0.8,0.8) near the equilibrium
population changes with respect to time for system (2.1). Each trajectory starts at a point (0.8,0.8,0.8) near the equilibrium 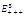 locally asymptotically stable: green-x , red-y, black-z. Here
locally asymptotically stable: green-x , red-y, black-z. Here