Rajan Arora, Sanjay Yadav
Indian Institute of Technology, Roorkee, Saharanpur Campus, Saharanpur U.P., 247001, India
Correspondence to: Sanjay Yadav, Indian Institute of Technology, Roorkee, Saharanpur Campus, Saharanpur U.P., 247001, India.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
The (G`/G)-expansion method is used for determining the exact traveling wave solutions of the Burgers-KdV and generalization of Huxley equations. The obtained solutions are compared with the solutions found by Wazwaz[18]. The (G`/G)-method is very powerful and easy tool for solving non-linear partial differential equations
Keywords:
(G`/G)-expansion method, Burgers KDV equation, generalization of Huxley equation, traveling wave solutions, exact solution
1. Introduction
Nonlinear equations in mathematical physics appear in various areas, such as fluid dynamics, plasma physics, optical fibers, solid state physics and other applications. A variety of powerful methods have been used to study the nonlinear equations such as the homotopy perturbation method[1], the variational iteration method[2], Hirotas bilinear methods[3], the sine-cosine function method[4-5], Jacobi elliptic method[6], the standard tanh and extended tanh methods[7-11], the exp-function method[12-13], the inverse scattering method[14] and so on. One of the most powerful and direct methods for constructing solutions of non-linear equations is the (G`/G)-expansion method[15- 17]. This method was first introduced by Wang et al.[15] and it has been widely used for finding various exact solutions of non-linear partial differential equations. The computer symbolic systems such as Maple and Mathematica allow us to perform complicated and tedious calculations The parameter 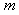 plays an important role in the (G`/G)- expansion method; it should be a positive integer to derive a closed form analytic solution. However, for non-integer values of
plays an important role in the (G`/G)- expansion method; it should be a positive integer to derive a closed form analytic solution. However, for non-integer values of 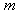 , we usually apply a transformation formula to overcome this difficulty.
, we usually apply a transformation formula to overcome this difficulty. 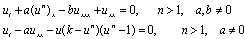 | (1) |
2 Analysis of the (G`/G)-expansion method
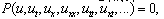 | (2) |
and so on for the other derivatives. Thus PDE (2) reduces to an ordinary differential equation (ODE)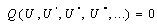 | (3) |
where the primes denote the derivative with respect to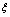 . Equation (3) is then integrated as long as all the terms contain derivatives, where integration constants are considered to be zero.Now, we assume that the solution of the ODE (3) can be expressed by a polynomial in (G`/G) as follows:
. Equation (3) is then integrated as long as all the terms contain derivatives, where integration constants are considered to be zero.Now, we assume that the solution of the ODE (3) can be expressed by a polynomial in (G`/G) as follows: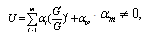 | (4) |
where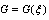 satisfies the second order linear ODE in the form
satisfies the second order linear ODE in the form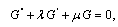 | (5) |
where 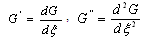 , and
, and  ,
, 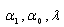 and
and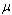 are real constants which are to be determined. Using (4) and (5), we obtain
are real constants which are to be determined. Using (4) and (5), we obtain 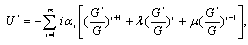 | (6) |
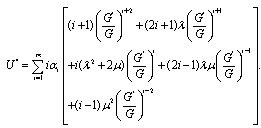 | (7) |
Using the general solution of (5), we have for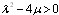
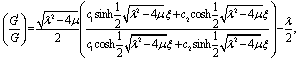 | (8) |
for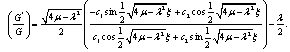 | (9) |
Also for 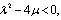
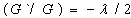 To determine U explicitly, we take the following four steps:Step 1. Determine the integer
To determine U explicitly, we take the following four steps:Step 1. Determine the integer 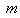 by substituting (4) along with (5) into (3), and balancing the highest order nonlinear term(s) and the highest order partial derivative.Step 3. Solve the system of algebraic equations obtained in step 2 for
by substituting (4) along with (5) into (3), and balancing the highest order nonlinear term(s) and the highest order partial derivative.Step 3. Solve the system of algebraic equations obtained in step 2 for 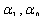 and
and 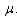 by use of Mathematica.Step 4. By substituting the results obtained in the above steps, we can obtain exact traveling wave solutions of (2).
by use of Mathematica.Step 4. By substituting the results obtained in the above steps, we can obtain exact traveling wave solutions of (2).
3. Applications
In this section, we apply the (G`/G)-expansion method to construct the traveling wave solution of Burgers-KdV and generalization of Huxley equations.
3.1. The Burgers-Kdv equation
The Burgers-Kdv equation is given by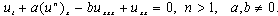 | (10) |
Using the transformation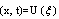 , where
, where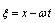 , the PDE is reduced to an ODE
, the PDE is reduced to an ODE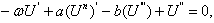 | (11) |
where the primes denote the derivative with respect to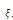 . Integrating once with respect to
. Integrating once with respect to 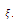 and taking constant of integration to be zero, (11) reduces to
and taking constant of integration to be zero, (11) reduces to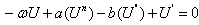 | (12) |
Balancing 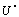 and
and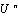 ,
,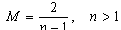 | (13) |
Using the transformation 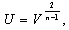 | (14) |
equation (12) converts to 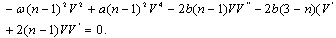 | (15) |
Now balancing 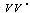 with
with 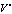 i.e.
i.e. 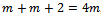 , we obtain
, we obtain 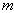 =1. Therefore, we assume the solution of (15) in the form
=1. Therefore, we assume the solution of (15) in the form 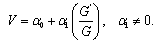 | (16) |
Using (6), (7) and (16), we obtain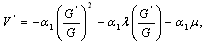 | (17) |
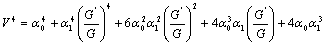 | (18) |
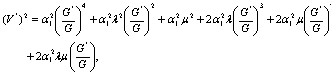 | (19) |
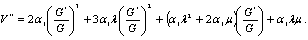 | (20) |
Now using (16)-(20) in (15) and equating the coefficients of 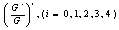 to zero, we obtain a system of algebraic equations in
to zero, we obtain a system of algebraic equations in 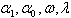 and
and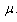 as follows:
as follows: 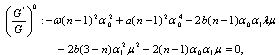 | (21) |
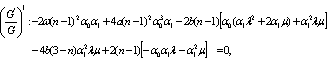 | (22) |
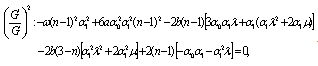 | (23) |
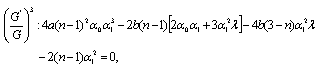 | (24) |
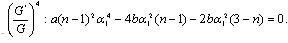 | (25) |
Solving the system of equations (21)-(25) by using MATHEMATICA, we obtain the following two sets of solutions for 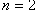 Set1:
Set1: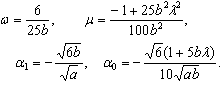 Set2:
Set2: 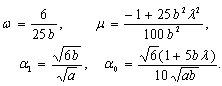 Hence, for Set 1:
Hence, for Set 1: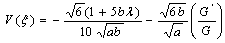 | (26) |
Now, using 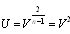
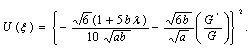 | (27) |
When 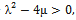 we obtain hyperbolic function solution of the Burgers-KdV equation (10) as
we obtain hyperbolic function solution of the Burgers-KdV equation (10) as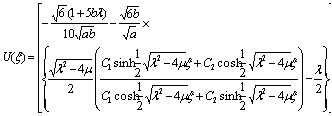 | (28) |
when 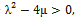 0, we obtain the trigonometric function solution of the Burgers-KdV equation (10) as
0, we obtain the trigonometric function solution of the Burgers-KdV equation (10) as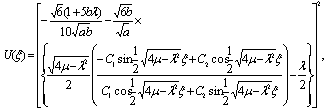 | (29) |
and when 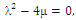
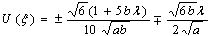 (30)If we set
(30)If we set 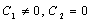 in (28), we obtain
in (28), we obtain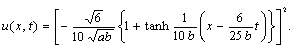 | (31) |
If we set 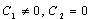 in (28), we obtain
in (28), we obtain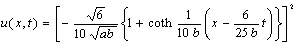 | (32) |
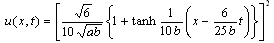 | (33) |
for  and
and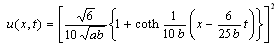 | (34) |
for 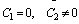
3.2. Generalization of Huxley equation
Consider a generalization of the Huxley equation 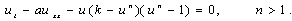 | (35) |
Proceeding as earlier, equation (35) is converted to the ODE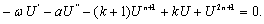 | (36) |
Now, balancing 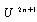 and
and 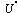 we find
we find 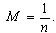 Using the transformation
Using the transformation 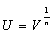 in (36), we obtain
in (36), we obtain 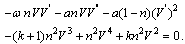 | (37) |
Now again balancing 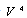 with
with 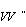 i.e.
i.e. 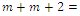
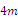 we obtain
we obtain 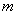 =1. Therefore,
=1. Therefore, 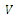 assumes the same form as in (16). Now, putting the different values of
assumes the same form as in (16). Now, putting the different values of 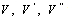 etc. from (16)-(20) in (37) and setting the coefficients of
etc. from (16)-(20) in (37) and setting the coefficients of 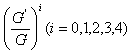 to zero we obtain a system of algebraic equations in
to zero we obtain a system of algebraic equations in 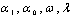 and
and 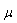 as follows:
as follows: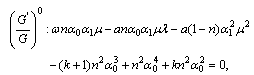 | (38) |
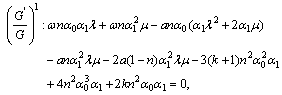 | (39) |
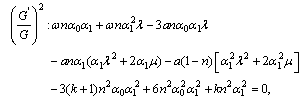 | (40) |
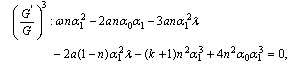 | (41) |
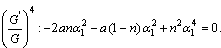 | (42) |
Fixing 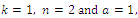 and then solving the system of equations (38)-(42) by MATHEMATICA, we obtain two sets of solutions:Set 1:
and then solving the system of equations (38)-(42) by MATHEMATICA, we obtain two sets of solutions:Set 1: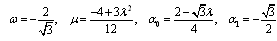 Set 2:
Set 2: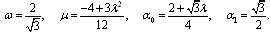 Therefore, the solution of the generalization of the Huxley equation (35) corresponding to Set 1 using
Therefore, the solution of the generalization of the Huxley equation (35) corresponding to Set 1 using 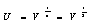
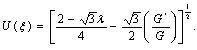 | (43) |
When 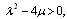
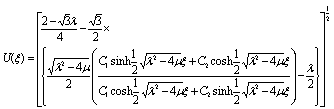 | (44) |
when 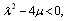
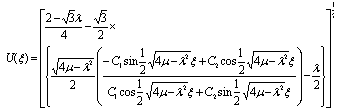 | (45) |
and when 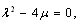
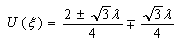 | (46) |
If we set 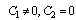 in (44), we obtain
in (44), we obtain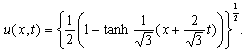 | (47) |
If we set 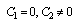 in (44), we obtain
in (44), we obtain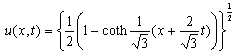 | (48) |
Similarly for Set 2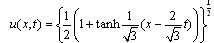 | (49) |
for 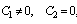 and
and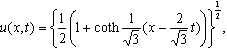 | (50) |
for 
4. Conclusions
(G`/G)-expansion method is used to obtain the exact solutions of the Burgers-KdV and generalization of Huxley equations. The solution method is very simple and effective. The solutions are expressed in the form of hyperbolic functions and the trigonometric functions. It is shown that this method is a good tool for handling non-linear partial differential equations. The solutions are compared with the solutions obtained by Wazwaz[18], and it is found that the solutions obtained are exactly same as determined by Wazwaz[18].
References
| [1] | He, J.H.: Application of Homotopy Perturbation Method to Nonlinear Wave Equations. Chaos, Solitons and Fractals 26, 695-700 (2005) |
| [2] | He, J.H., Wu, X.H.: Construction of Solitary Solution and Compaction-Like Solution by Variational Iteration Method. Chaos Solitons and Fractals 29, 108-113 (2006) |
| [3] | Hirota, R.: Exact Solution of the Kdv Equation for Multiple Collisions of Solitons. Physical Review Letters 27, 1192-1194 (1971) |
| [4] | Borhanifar, A., Jafari, H., Karimi, S.A.: New solitary wave solutions for the bad Boussinesq and good Boussinesq equations, Numer. Methods for Partial Differential Equations 25, 1231–1237 (2009) |
| [5] | Borhanifar, A., Jafari, H., Karimi, S.A.: New solitons and periodic solutions for the Kadomtsev–Petviashvili equation. Nonlinear Sci. Appl. 4, 224–229. (2008) |
| [6] | Liu, G. T., Fan, T. Y.: New applications of developed Jacobi elliptic function expansion methods. Phys. Lett. A 345, 161–166 (2005) |
| [7] | Wazwaz, A.M.: Exact solutions to the double sinh-Gordan equation by tanh method and a variable separated ode method. Compt. Math. Appl. 501685-1696 (2005) |
| [8] | Malfliet, W., Hereman, W.: The tanh method: exact solutions of nonlinear evolution and wave equations. Phys. Scr. 54, 563–568 (1996) |
| [9] | Wang, M.L.: Exact solution for a compound KdV-Burgers equations. Phys. Lett. A 213, 279–287 (1996) |
| [10] | Malfliet, W.: Solitary wave solutions of nonlinear wave equations. Am. J. Phy. 60, 650–658 (1992) |
| [11] | Malfliet, W., Hereman, W.: The tanh method: II. Perturbation technique for conservative systems. Phys Scr. 54, 569–575 (1996) |
| [12] | Zhou, X.W., Wen, Y.X., He J.H.: Exp-function method to solve the nonlinear dispersive k(m, n) equations, Int. J. Nonlinear Sci. Numer. Simul. 9, 301–306 (2008) |
| [13] | Liu, G.T, Fan, T.Y.: New applications of developed Jacobi elliptic function expansion methods. Phys. Lett. A 345, 161–166 (2005) |
| [14] | Ablowitz, M.J., Segur, H.: Solitons and Inverse Scattering Transform. SIAM, Philadelphia (1981) |
| [15] | Wang, M.L., Li, X. Zhang, J.: The (G’/G)-expansion method and traveling wave solutions of nonlinear evolution equations in mathematical physics. Phys. Lett. A 372 417–423 (2008) |
| [16] | Aslan, İ.: Exact and explicit solutions to some nonlinear evolution equations by utilizing the (G’/G)-expansion method. Appl. Math. Comput. 215, 857–863 (2009) |
| [17] | Bekir, A.: Application of the (G’/G)-expansion method for nonlinear evolution equations. Phys. Lett. A 372, 3400–3406 (2008) |
| [18] | Wazwaz, A.M.: Travelling wave solutions of generalized forms of Burgers, Burgers-KDV and Burgers-Huxley equations. Appl. Math. Comput 169, 639-656 (2005) |
 plays an important role in the (G`/G)- expansion method; it should be a positive integer to derive a closed form analytic solution. However, for non-integer values of
plays an important role in the (G`/G)- expansion method; it should be a positive integer to derive a closed form analytic solution. However, for non-integer values of 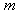 , we usually apply a transformation formula to overcome this difficulty.
, we usually apply a transformation formula to overcome this difficulty. 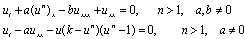
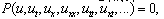
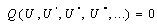
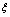 . Equation (3) is then integrated as long as all the terms contain derivatives, where integration constants are considered to be zero.Now, we assume that the solution of the ODE (3) can be expressed by a polynomial in (G`/G) as follows:
. Equation (3) is then integrated as long as all the terms contain derivatives, where integration constants are considered to be zero.Now, we assume that the solution of the ODE (3) can be expressed by a polynomial in (G`/G) as follows: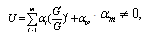
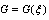 satisfies the second order linear ODE in the form
satisfies the second order linear ODE in the form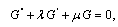
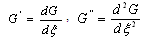 , and
, and 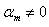 ,
, 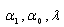 and
and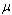 are real constants which are to be determined. Using (4) and (5), we obtain
are real constants which are to be determined. Using (4) and (5), we obtain 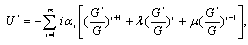
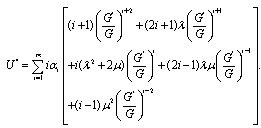
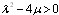
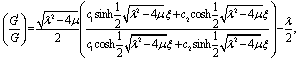
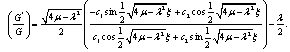
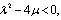
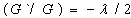 To determine U explicitly, we take the following four steps:Step 1. Determine the integer
To determine U explicitly, we take the following four steps:Step 1. Determine the integer 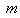 by substituting (4) along with (5) into (3), and balancing the highest order nonlinear term(s) and the highest order partial derivative.Step 3. Solve the system of algebraic equations obtained in step 2 for
by substituting (4) along with (5) into (3), and balancing the highest order nonlinear term(s) and the highest order partial derivative.Step 3. Solve the system of algebraic equations obtained in step 2 for 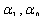 and
and 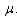 by use of Mathematica.Step 4. By substituting the results obtained in the above steps, we can obtain exact traveling wave solutions of (2).
by use of Mathematica.Step 4. By substituting the results obtained in the above steps, we can obtain exact traveling wave solutions of (2).
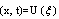 , where
, where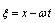 , the PDE is reduced to an ODE
, the PDE is reduced to an ODE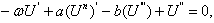
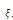 . Integrating once with respect to
. Integrating once with respect to 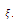 and taking constant of integration to be zero, (11) reduces to
and taking constant of integration to be zero, (11) reduces to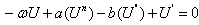
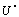 and
and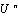 ,
,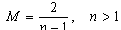
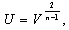
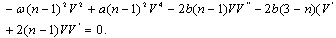
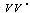 with
with 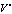 i.e.
i.e. 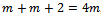 , we obtain
, we obtain 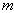 =1. Therefore, we assume the solution of (15) in the form
=1. Therefore, we assume the solution of (15) in the form 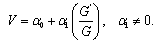
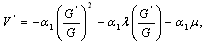
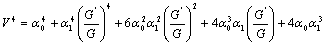
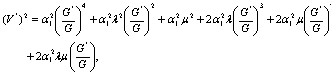
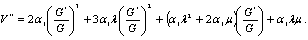
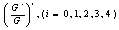 to zero, we obtain a system of algebraic equations in
to zero, we obtain a system of algebraic equations in 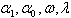 and
and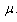 as follows:
as follows: 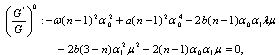
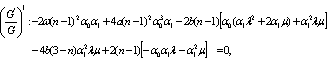
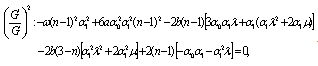
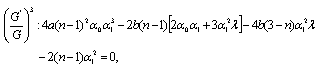
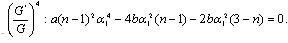
 Set1:
Set1: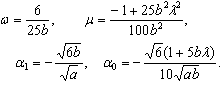 Set2:
Set2: 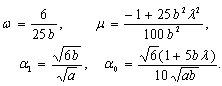 Hence, for Set 1:
Hence, for Set 1: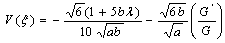
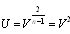
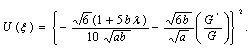
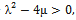 we obtain hyperbolic function solution of the Burgers-KdV equation (10) as
we obtain hyperbolic function solution of the Burgers-KdV equation (10) as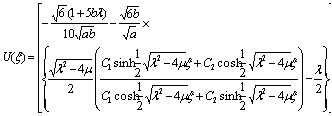
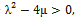 0, we obtain the trigonometric function solution of the Burgers-KdV equation (10) as
0, we obtain the trigonometric function solution of the Burgers-KdV equation (10) as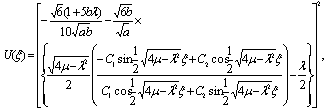
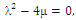
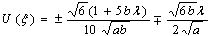 (30)If we set
(30)If we set 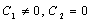 in (28), we obtain
in (28), we obtain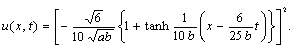
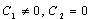 in (28), we obtain
in (28), we obtain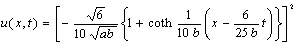
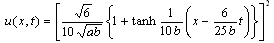
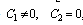 and
and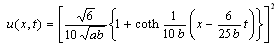
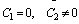
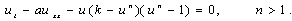
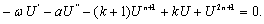
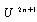 and
and 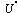 we find
we find 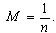 Using the transformation
Using the transformation 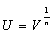 in (36), we obtain
in (36), we obtain 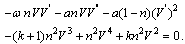
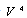 with
with 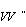 i.e.
i.e. 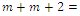
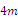 we obtain
we obtain 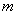 =1. Therefore,
=1. Therefore, 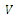 assumes the same form as in (16). Now, putting the different values of
assumes the same form as in (16). Now, putting the different values of 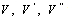 etc. from (16)-(20) in (37) and setting the coefficients of
etc. from (16)-(20) in (37) and setting the coefficients of 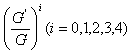 to zero we obtain a system of algebraic equations in
to zero we obtain a system of algebraic equations in 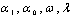 and
and 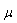 as follows:
as follows: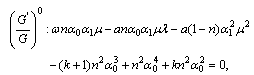
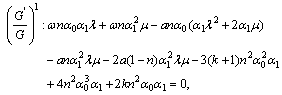
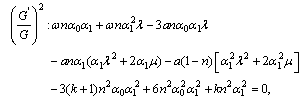
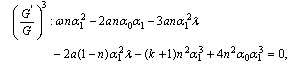
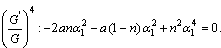
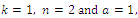 and then solving the system of equations (38)-(42) by MATHEMATICA, we obtain two sets of solutions:Set 1:
and then solving the system of equations (38)-(42) by MATHEMATICA, we obtain two sets of solutions:Set 1: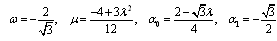 Set 2:
Set 2: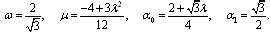 Therefore, the solution of the generalization of the Huxley equation (35) corresponding to Set 1 using
Therefore, the solution of the generalization of the Huxley equation (35) corresponding to Set 1 using 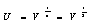
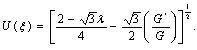
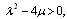
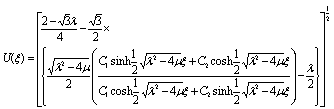
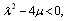
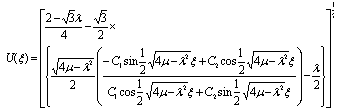
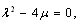
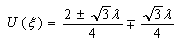
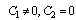 in (44), we obtain
in (44), we obtain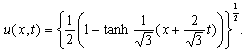
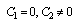 in (44), we obtain
in (44), we obtain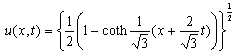
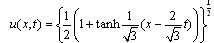
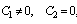 and
and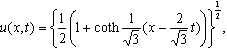
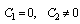
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML