| [1] | Appell, J.M., Kalitvin,A.S.andZabrejko, P.P., Partial integral operators and integro-differential equations,M.Dekkar, New York(2000). |
| [2] | Bahuguna, D. and Dabas, J., Existence and uniqueness of a solution to a PIDE by the method of lines, Electronic Journal of Qualatative Theory of Differential Equations, 4(2008)1-12. |
| [3] | Pachapatte, B.G., On some new integral and integro-differntial inequalities in two independent variables and their applications, Journal of Differential Equations, 33(1979)249-272. |
| [4] | Yanik, E.G. and Fairweather, G., Finite element methods for parabolic and hyperbolic partial integro-differential equations, Nonlinear Analysis: Theory, Method and Applications, 12(1988)785-809. |
| [5] | Dehghan, M. and Shakeri, F., Solution of parabolic integro-differential equations arising in heat conduction in materials with memory via He’s variational iteration technique, International Journal For Numerical Methods In Biomedical Engineering, 26(2010)705-715. |
| [6] | Dehghan, M., Solution of a partial integro-differential equation arising from viscoelasticity, International Journal of Computational Mathematics,83(2006)123-129. |
| [7] | Pao, C.V., Solution of a nonlinear integro-differential system arising in Nuclear reactor dynamics, Journal Of Mathematical Analysis And Application, 48(1974)470-492. |
| [8] | Pachapatte, B.G., On a nonlinear diffusion system arising in reactor dynamics, Journal Of Mathematical Analysis And Applications, 94(1983)501-508. |
| [9] | Sachs, E.W. and Strauss, A.K., Efficient solution of a partial integro-differential equation in finance, Applied Numerical Mathematics, 58(2008)1687-1703. |
| [10] | Abeergel, F. and Tachet, R., A nonlinear partial integro-differential equation from mathematical finance, AIMS Journal, 10(2010)10-20. |
| [11] | Hepperger, P., Hedging electricity swaptions using partial integro-differential equations, Stochastic Processes And Their Applications, 122(2012)600-622. |
| [12] | Zadeh, K.S., An integro-partial differential equation for modeling biofluids flow in fractured biomaterials, Journal Of Theoretical Biology, 273(2011)72-79. |
| [13] | Debnath, L. and Bhatt, D., Integral transforms and their applications, CRC Press (2007). |
| [14] | Rehman, M., Integral equations and their applications,WIT Press(2007). |
| [15] | Schiff, J.L., The Laplace transform theory and applications, Springer, New York (1999). |
| [16] | Xiang, Tan-yong, Guo,Jia-qi, A Laplace transform and Green function method for calculation of water flow and heat transfer in fractured rocks, Rock And Soil Mechanics, 32(2)(2011)333-340. |
| [17] | Alquran, M.T., AL-khaled, K., Ali, M. and Taany, A., The combined Laplace transform- differential transform method for solving linear non-homogeneous partial differential equations, Journal Of Mathematics Computer science, 2(2012)690-701. |
| [18] | Merdan, M., Yildirim, A., Gokdogan, A. and Mohyud-dins, T., Coupling of homotopy perturbation, Laplace transform and pade Approximants for nonlinear oscillatory systems, World Applied Sciences Journal, 16(3)(2012)320-328. |
| [19] | Aminikhah, H., The combined Laplace transform and new homotopy perturbation methods for stiff systems of ordinary differential equations, Applied Mathematical Modeling, 36(2012)3638-3644. |
| [20] | Kexue, Li, Jigen, P., Laplace transform and fractional differential equations, Applied Mathematics Letters, 24(2011)2019-2023. |

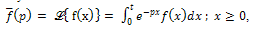 ,(whenever integral on RHS exists)where, x ≥0, p is real and ℒis the Laplace transform operator.Convolution Theorem:If
,(whenever integral on RHS exists)where, x ≥0, p is real and ℒis the Laplace transform operator.Convolution Theorem:If 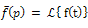 and
and 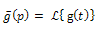 then
then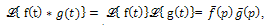 where,
where, 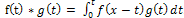 .
.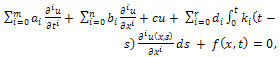 (*) (with prescribed conditions)where
(*) (with prescribed conditions)where 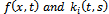 are known functions.
are known functions. 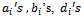 and c are constants or the functions of x.Taking Laplace transform on both sides of PIDE (*) with respect to t we get,
and c are constants or the functions of x.Taking Laplace transform on both sides of PIDE (*) with respect to t we get,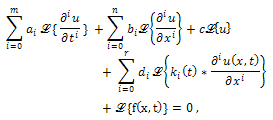
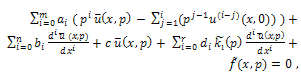 (**) where,
(**) where, 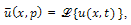
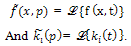 Equation (**) is an ordinary differential equation in
Equation (**) is an ordinary differential equation in 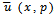 . Solving this ordinary differential equation and taking inverse Laplace transform of
. Solving this ordinary differential equation and taking inverse Laplace transform of 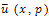 , we get a solution
, we get a solution 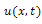 of (*).
of (*).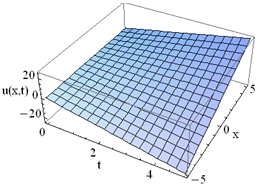
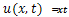
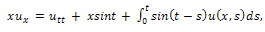
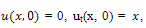
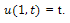
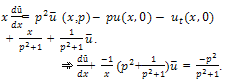
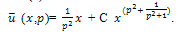
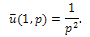
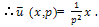
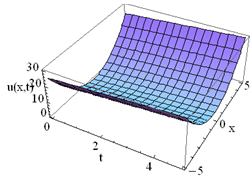
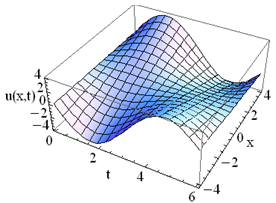
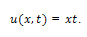 The solution of (1) is plotted in the Fig.1.Example 2. Consider the PIDE
The solution of (1) is plotted in the Fig.1.Example 2. Consider the PIDE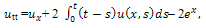
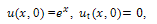
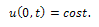
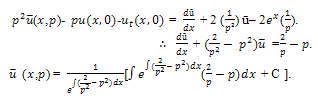
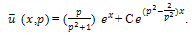
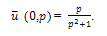
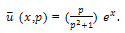
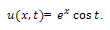
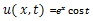
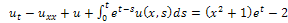
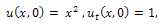
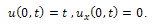
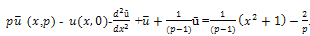
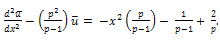
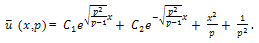
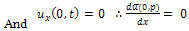
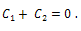
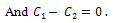
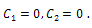 Equation (20) becomes,
Equation (20) becomes,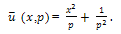 Taking inverse Laplace transform we get,
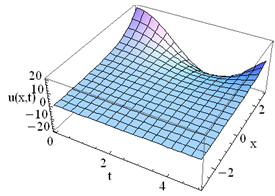
Taking inverse Laplace transform we get,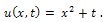 This is an exact solution of (15).Figure 3 represents the graph of
This is an exact solution of (15).Figure 3 represents the graph of 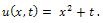
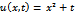
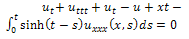
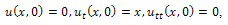
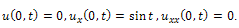
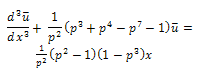
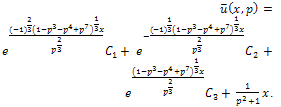
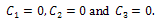 Therefore equation (29) becomes,
Therefore equation (29) becomes,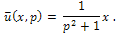 Taking inverse Laplace transform we get,
Taking inverse Laplace transform we get,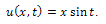
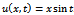
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML