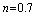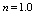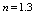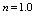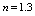1. Introduction

The recent trend in Mechanical industry shows that it designs machines with high operating speeds and heavy load carrying capacity. Therefore, lubrication of modern machines has been a great challenge and an emerging area of interest for the researchers around the world. In recent times, experimental researches have shown clear evidence that the use of lubricants with variable viscosity can improve the lubricant properties relative to that of lubricants with constant viscosity. Therefore, the interest has been increasing to use the lubricants with variable viscosity called non-Newtonian lubricants, in particular, characterized by a yield-value known as visco-plastic lubricants. Hence, visco-plastic lubricants are gaining importance in lubrication analysis. Some of the important visco-plastic fluid models are Bingham Plastics, Casson fluids and Herschel-Bulkley fluids.

Ghosh and Majumdar[7] investigated the effects of recessvolume compressibility on the dynamic characteristics of an externally pressurized bearings using Newtonian lubricant. Hsaegawa[8] has studied theoretically, the squeeze film flow of an incompressible viscous Newtonian fluid between a curved disc and a plane wall at rest. Elsharkawy et al.[5] introduced a mathematical model and obtained numerical solutions for an externally pressurized circular porous bearing using Newtonian fluid as lubricant. Serdar Baris[17] applied the mixture theory of two chemically inert incompressible Newtonian fluids to some simple unsteady flows in the annular region between two infinitely long coaxial cylinders.

In all these studies, authors have considered Newtonian fluids as lubricants. Recently, the researchers intend to use non-Newtonian fluids characterized by a yield-value called visco-plastic fluids as lubricants. The advent of such rheological lubricants has made the theory of lubrication more efficient. Bingham, Casson and Herschel-Bulkley fluids are some of the visco-plastic fluids used as lubricants in the industries.

The effects of Bingham lubricant, on slider, thrust, Journal and squeeze film bearings have been analyzed by many researchers. Covey and Stanmore[4] obtained theoretical and experimental results for the flow of Bingham fluid in a parallel-plate plasto-meter and discussed the presence and formations of yield surface. Papanastasiou[15] analyzed the steady, two-dimensional flow of Bingham fluid by considering modified constitutive equation. Kandasamy[12] analyzed theoretically and obtained numerical solutions for the bearing performances of an externally pressurized thrust bearing lubricated with non-Newtonian fluids. Gertzos et al.[6] developed 3-dimensional CFD model to study the behavior and performance characteristics of a Journal bearings lubricated with Bingham fluid. Jaw-Ren Lin[11], on the basis of the micro-continuum theory, has investigated the squeeze film characteristics between a sphere and a flat plate based on couple stress fluid model.

The Herschel-Bulkley fluid model represents both shear thinning and shear thickening materials. It is the combination of both Bingham plastic and power-law fluids and is also known as yield-power law fluids. Examples of such materials are greases, colloidal suspensions and starch pastes. The blood also behaves like Herschel-Bulkley fluids, while flowing through narrow tubes.

Chaturani and Narasimman[3] have theoretically investigated the flow of Casson and Herschel-Bulkley fluids in a cone-plate viscometer. Adams et al.[1] have implemented finite element analysis of a squeeze flow for a material that exhibits elasto- visco-plasticity and the numerical results have been verified with experimental measurements. Meetan[14] has carried out both theoretical and experimental investigation of the force required to squeeze a Herschel-Bulkley material. Zhang et al.[22] have numerically analyzed the behavior of Herschel-Bulkley fluid in between two ellipsoid rollers. The effects of fluid inertia have been analyzed theoretically by Vishwanath and Kandasamy[20] in a circular squeeze film bearing with constant squeeze motion using Herschel-Bulkley lubricant. It has been shown that the fluid inertia forces indeed enhance the performances of the bearing. Jayakaran Amalraj et.al[23] studied theoretically the performance of an externally pressurized thrust bearing by means of sinusoidal injection of the Herschel-Bulkley lubricant.

Tichy[18] studied the inertia effects in hydrodynamic lubrication by a linearization method and applied it to the squeeze film damper bearing. Inertia effects on the operating characteristics of Journal bearing have been analyzed by You and Lu[21]. Batra and Kandasamy[2] have analyzed the inertia effects in squeeze film bearing using Bingham fluid as lubricant. J.S. Roy et.al[4] investigated the effects of inertia forces in an externally pressurized thrust bearing with converging and diverging fluid film using visco-elastic lubricant. Usha and Vimala[19] have discussed about inertia effects in circular squeeze films containing a central air bubble. The flow of a squeeze film containing central air bubble under sinusoidal squeeze motion has been investigated by Hashimoto[9] using the method of averaging inertia terms.

In the present work, the effects of inertia in an externally pressurized thrust bearing lubricated with Herschel-Bulkley fluid have been analyzed. During the operations of the bearings, the maximum viscous shearing stresses arise in the region between the plates. Therefore, there may be a region in the fluid film where the shearing stresses do not exceed the yield value of the lubricant and there by a core with zero velocity gradients is formed. The flow occurs in the region where the shear stress exceeds the yield value. The shape and extent of the core along the radius for various values of the Herschel-Bulkley number and the power-law index have been numerically determined. The flow is confined to the region between the core and the circular plates of the bearing. Numerical solutions have been obtained for the bearing performances such as pressure distribution and load capacity for different values of Herschel-Bulkley number, power-law index and Reynolds number.

2. Formulation of the Problem

The Geometry of the problem is as shown in Figure.1

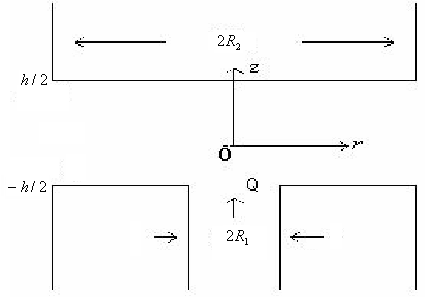Figure 1. Geometry of an Externally Pressurized Thrust Bearing

Consider an isothermal, incompressible steady flow of a time independent Herschel-Bulkley fluid injected between two circular plates, of the bearing, separated by a distance,h . Let R₁be the radius of the film inlet, and R₂ be the radius of the film outlet P, represents the pressure of the film, P_n represents the atmospheric pressure and the density of the fluid. The cylindrical polar coordinates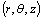with axial symmetry have been considered. The origin is fixed at the centre of the film clearance, r , measuring the distance along the radial direction and Z, along the axis normal to the bearing. Let v_r and 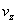be the velocity components along r and z directions respectively.

The three dimensional constitutive equation of the Herschel-Bulkley fluids is given by

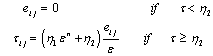(1)

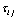Where are the deviatory stress components, 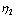, 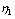and n are constants namely the yield stress, consistency index and power-law index respectively. Here 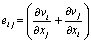represents rate of deformation components and 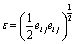is second strain invariant.

Further, for all practical purposes the one -dimensional form of equation (1) is given by

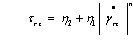(2)

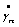where, , represents the shear rate.

In those regions of the film, where the shear stress is less than the yield value, there will be a core formation, which will move with constant velocity, v_c. Let the boundaries of the core be 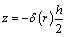and 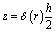which is shown in Figure.2.

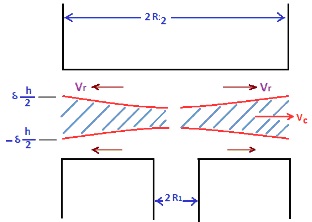Figure 2. Shape of the Core in an externally pressurized thrust bearing

Applying the basic assumptions of lubrication theory for thin films, the equations governing the flow of a Herschel-Bulkley fluid in an externally pressurized thrust bearing including inertia forces will be

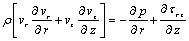(3)

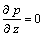(4)

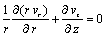(5)

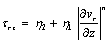(6)

The equations (3), (4) and (6) together with the continuity equation (5) are to be solved under the following boundary conditions:

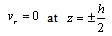(7)

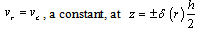(8)

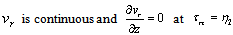(9)

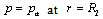(10)

3. Solution of the Problem

Averaging the inertia terms in the momentum equation (3) by assuming it to be a constant over the film thickness , leads to

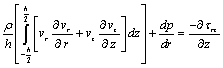(11)

Using the continuity equation (5) and boundary conditions (7) and (8) in (11), it is reduced to

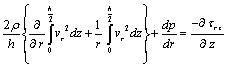(12)

For an externally pressurized thrust bearing, the modified pressure gradient is defined as

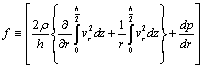(13)

Using (13) in (12), it becomes

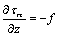(14)

Integrating (14),

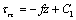(15)

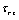Substituting from equation (15) into equation (6) and using the boundary the conditions (7) and (8), the velocity distribution in the flow region will be

,

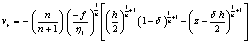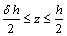(16)

and the core velocity will be

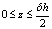(17)

Considering the equilibrium of an element of the core in the fluid, equation (14) becomes

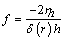(18)

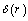Where represents the thickness of the core.

The equation of conservation of mass which depends on the configuration of the bearing is given by

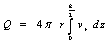(19)

Using the velocity expressions (16) and (17) in (19), it is found that

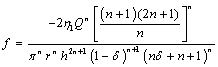(20)

Eliminating f from equations (18) and (20), an algebraic equation for determining the thickness of the core has been obtained as,

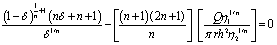(21)

Further, substituting the expressions (16), (17) and (20) in (11),

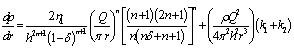(22)

Where

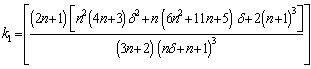
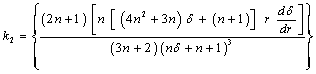By introducing the following non-dimensional quantities,

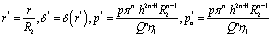the non-dimensional form of equation (21) can be expressed as

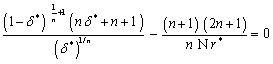(24)

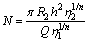Where is called the yield number (or) Herschel-Bulkley number.

The core thickness can be determined from the above non-linear algebraic equation using any iterative technique. The root of equation (24), 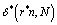which is positive and less than unity, determines the yield surface, between the plates. The core thickness is determined for various values of , n and N

The pressure gradient expression in non-dimensional form is obtained as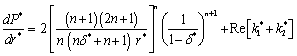

(25)

Where

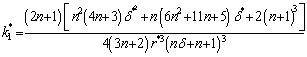
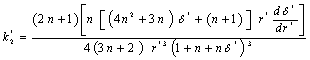The expression for the pressure distribution can be obtained by integrating (25) and using the boundary condition (7) as

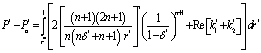(26)

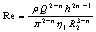and is the Reynolds number.

The load capacity for an externally pressurized thrust bearing is,

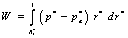(27)

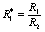where, (i.e) 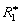is the ratio of the inlet to the outlet of the bearing.

The above integral is evaluated numerically for various values of power-law index, Reynolds number and Herschel-Bulkley number.

4. Results and Discussion

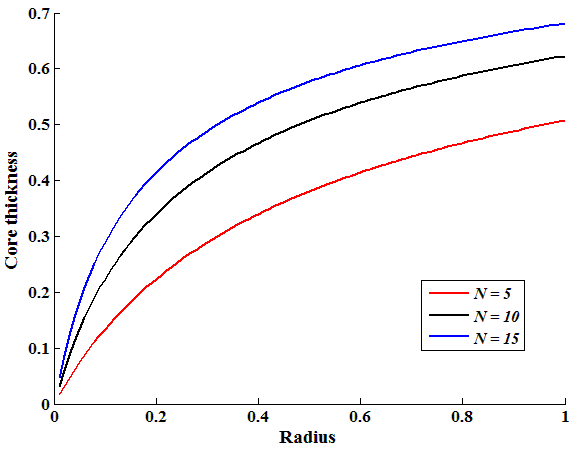
The thickness of the core along the radial direction for various values of power-law index(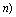and Herschel-Bulkley number 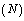have been computed numerically and are shown in the Figures. 3-5.

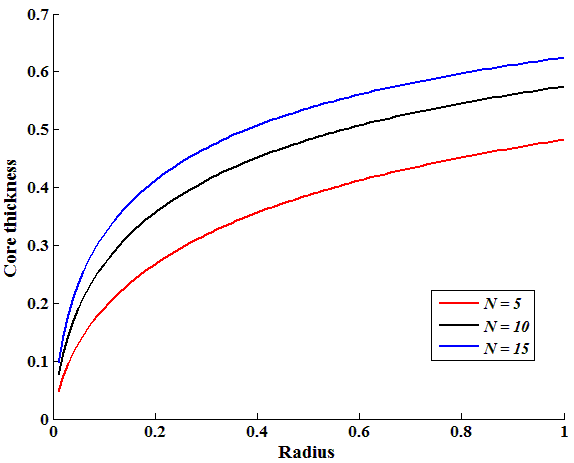Figure 3. Core thickness variation along the radius for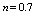

Figure 4. Core thickness variation along the radius for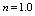

Figure 5. Core thickness variation along the radius for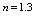

The plug core occurs symmetrically in the middle of the region between the circular plates. The thickness of the core along the radial direction increases from centre to the periphery. It has also been observed that for a given power-law index, the thickness of the core increases with the increase in Herschel-Bulkley number. Moreover, there is an increase in the core thickness with increase in power-law index for a particular Herschel-Bulkley number.

The velocity profiles for various Herschel-Bulkley number numbers along the axial direction at different radial positions have been obtained and are shown in Figure.6.

Figure 6. Velocity Profile for a particular power-law index

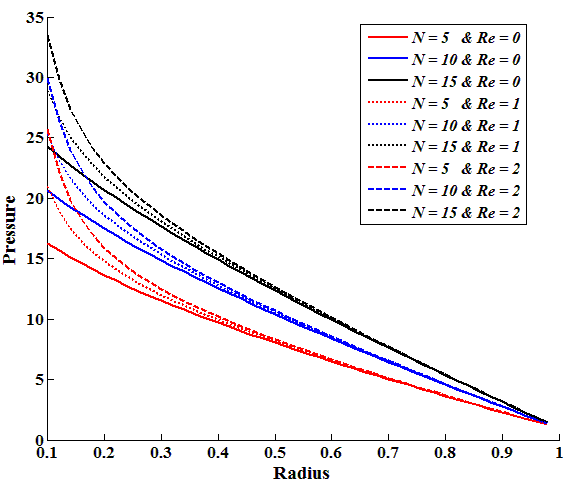Figure 7. Inertia effects on Pressure distribution for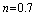

Figure 8. Inertia effects on Pressure distribution for

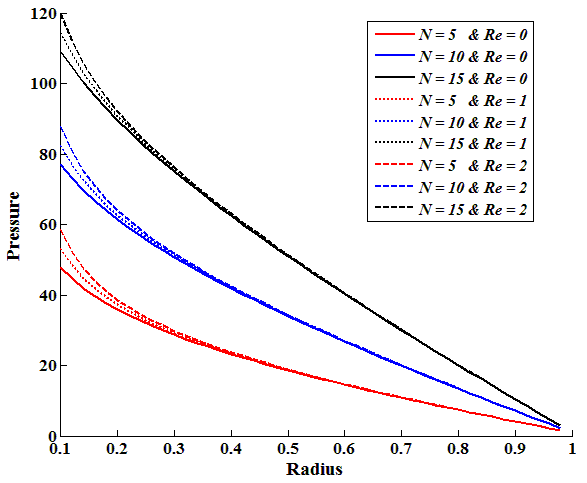Figure 9. Inertia effects on Pressure distribution for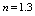

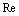The presence and thickness of the core is very much reflected in the velocity profile. Further, it has been found that in the limiting case, as N tends to zero, the velocity profile becomes parabolic which represents Newtonian fluid.

The distribution of film pressure in the radial direction for various values of the Reynolds number (), Herschel-Bulkley number and power-law index, and are shown in the Figures. 7-9.

The pressure is found to be high at the centre and decreases towards the periphery of the bearing along the radial direction. It has been observed that there is a significant increase in the pressure for the fluids with high Herschel-Bulkley number for a specific power-law index. Further, there is a considerable increase in the pressure distribution due to the increase in power-law index of the fluid. The increase in pressure is also observed as the Reynolds number increases. However, the amount of increase in pressure due to Reynolds number is marginal. Moreover, the effects of inertia on pressure distribution are found to be appreciable near the centre of the bearing.

The results of load-carrying capacity for different values of power-law index, Herschel-Bulkley number and Reynolds number are tabulated in the Tables 1 – 3.

Table 1. Load capacity values for N and Re for       N/Re 0 1 2 3 4 5 2.7773 2.8425 2.8485 2.8537 2.8586 10 2.8617 2.927 2.933 2.9383 2.9431 15 2.946 3.0116 3.0175 3.0228 3.0276 20 3.0304 3.0961 3.102 3.1073 3.1121 25 3.1148 3.1806 3.1866 3.1918 3.1967

Table 2. Load capacity values for N and Re for       N/Re 0 1 2 3 4 5 4.1511 4.239 4.2573 4.2751 4.2927 10 4.2423 4.3303 4.3486 4.3664 4.384 15 4.3335 4.4216 4.4399 4.4577 4.4753 20 4.4246 4.5129 4.5312 4.549 4.5666 25 4.5158 4.6042 4.6225 4.6403 4.6579

Table 3. Load capacity values for N and Re for       N/Re 0 1 2 3 4 5 6.3401 6.4713 6.522 6.5765 6.6341 10 6.4391 6.5705 6.6211 6.6756 6.7333 15 6.5382 6.6697 6.7203 6.7748 6.8325 20 6.6372 6.7689 6.8195 6.874 6.9317 25 6.7362 6.8681 6.9187 6.9732 7.0308

It has been observed that the load carrying capacity of the bearing increases with the increase in Herschel-Bulkley number for a specific power-law index. For a particular Herschel-Bulkley number, the load carrying capacity increases significantly with the increase in power-law index. However, the effect of fluid inertia on the load carrying capacity is found to be marginal.

The percentage of increase in load carrying capacity for different values of power-law index, Herschel-Bulkley number and Reynolds number are given in the Tables 4 – 6.

Table 4. Percentage variation in Load capacity for       N/Re 0 1 2 3 4 5 0 2.3491 2.5629 2.7527 2.9267 10 0 2.285 2.4924 2.6766 2.8454 15 0 2.2245 2.4259 2.6048 2.7687 20 0 2.1674 2.3631 2.537 2.6963 25 0 2.1134 2.3038 2.4729 2.6279

Table 5. Percentage variation in Load capacity for       N/Re 0 1 2 3 4 5 0 2.116 2.5561 2.9859 3.4088 10 0 2.0742 2.5047 2.9252 3.3389 15 0 2.0341 2.4554 2.867 3.2721 20 0 1.9956 2.4082 2.8113 3.2079 25 0 1.9587 2.3629 2.7578 3.1464

Table 6. Percentage variation in Load capacity for       N/Re 0 1 2 3 4 5 0 2.0691 2.8682 3.7276 4.6375 10 0 2.0398 2.8264 3.6726 4.5685 15 0 2.0113 2.7859 3.6193 4.5015 20 0 1.9836 2.7467 3.5675 4.4366 25 0 1.9568 2.7086 3.5173 4.3735

It has been observed that the percentage of increase in load carrying capacity due to inertia effect is significant only for those fluids with low Herschel-Bulkley number where as this percentage of increase decreases with the increase in Herschel-Bulkley number for any power-law index and Reynolds number. Moreover, the percentage of increase in the load carrying capacity increases significantly as the Reynolds number increases.

The results corresponding to Re = 0 which exhibits the inertia less effects on the pressure distribution and the load carrying capacity of the bearing are found to be in good agreement with the results of Kandasamy et.al[13]. Similarly, the results corresponding to n=1 are in agreement with the results obtained by Jayakaran Amalraj et.al[10].

5. Conclussions

The above theoretical investigation reveals that the increase in Herschel-Bulkley number and power-law index significantly enhance the bearing performances such as pressure distribution and load carrying capacity. However, the effect of fluid inertia on the bearing performances is found to be marginal that itself near the centre of the bearing.

ACKNOWLEDGEMENTS

The authors (1) and (2) wish to thank the management of SSn college of Engineering for providing the necessary facilities, support and encouragement to carry out this research work.