-
Paper Information
- Next Paper
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Computational and Applied Mathematics
p-ISSN: 2165-8935 e-ISSN: 2165-8943
2012; 2(3): 73-78
doi: 10.5923/j.ajcam.20120203.02
Investigation of the Efficiency of Moment Method Solution Based on Expansion Functions Defined in the Infinite Domain for Electrostatic Problems
T. Teper, H. Matzner, P. Malits
Department of Communication Engineering, Faculty of Engineering, HIT - Holon Institute of Technology, Golomb 52, Holon 58102, Israel
Correspondence to: H. Matzner, Department of Communication Engineering, Faculty of Engineering, HIT - Holon Institute of Technology, Golomb 52, Holon 58102, Israel.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
The efficiency of the Moment Method (MM) when the expansion functions are defined in the infinite domain is checked. It is shown that efficient solution is obtained when the expansion functions obey the known physical behaviour of the fields. The age-old problem of the thin, charged disk is solved by the MM for which an electric field component is expanded outside the body. This solution is compared to the known analytic solution and to the MM solution for which the surface charge density is expanded on the finite disk. An excellent agreement between the analytical solution and the MM solution based on expansion functions defined in the infinite domain was achieved.
Keywords: Moment Method, Entire Domain, Infinite Domain
Article Outline
1. Introduction
- Moment Method (MM) is used frequently in solving electromagnetic problems[1]. Different expansion (basis) functions and test functions were checked during the last years in order to get more accurate and fast converging solutions. The inclusion of the edge behaviour of the fields in the expansion functions in order to get more accurate and fast converging solutions is addressed in many papers. For example[2] deals with the characterization of an infinite array microstrip reflectarray elements, and it is said that a complete set of trigonometric functions which do not enforce the correct edge conditions shows a slow rate of convergence of the solution. In[3] there is a use of MM basis functions containing the 90o conducting edge singularity behaviour to efficiently solve an infinite array of stub-loaded rectangular waveguides. It was shown, for example, by[4] that while expansion functions exactly obey the known physical behaviour of the fields, the solution obtained is more accurate and fast converging, as compared to cases when the expansion functions do not obey the known physical behaviour of the field. Fuzzy basis functions which can approximate any function to an arbitrary degree of accuracy are applied in[5]. In this method the user's insight can be taken into account easily and systematically resulting in a better approximation. Recently large complex structures are solved by the MM by dividing the structure to sub-domains, where few expansion functions are needed for each sub-domain. Use of these basis functions leads to a significant reduction in the number of unknowns, and results in a substantial size reduction of the MM matrix[6,7].In this paper we check the efficiency of an MM solution when the expansion functions are defined in the infinite domain. To do this we choose a simple electromagnetic problem (a toy model) for which the analytic solution is known, and compare our MM solution based on expansion functions defined in the infinite domain to the analytic solution and to an MM solution based on expansion functions defined in the finite domain. The relevant problem chosen is the isolated flat, infinitely thin, ideal conducting circular disc of radius R, with a total charge q placed on it. We choose to expand the ρ component of the electric field outside the disk, where the expansion functions obey the exact physical behaviour of the field near the edge of the disk and at infinity. This solution in compared to the MM solution where the expansion functions describe the surface charge density on the finite disk.The structure of the paper is as follows: chapter II describes the formulation of the problem and includes the analytical solution and the MM solutions. Chapter III deals with the selection of the expansion functions, and numerical results are presented in chapter IV. Finally, conclusions are discussed in chapter V. Some relevant mathematical calculations are presented in the Appendix.
2. Formulation
2.1. Geometry and Analytic Solution
- The thin, charged disk is shown in figure 1. The radius of the disk is R and the total charge on it is q
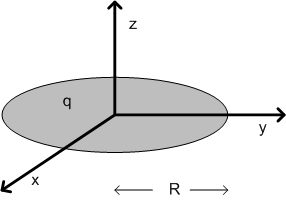 | Figure 1. Isolated, infinitely thin, flat, circular conducting disk of radius R with a total charge q placed on it |
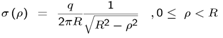 | (1) |
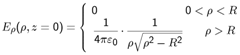 | (2) |
2.2. The Fields Related to the Problem
- Laplace equation around the disk is specified by
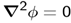 | (3) |
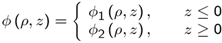 | (4) |
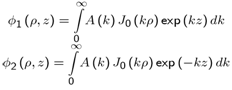 [8], and where J0 (.) is the Bessel function of the first kind[9]. A(k) will be expressed by the MM expansion functions.. The electric field components are given by
[8], and where J0 (.) is the Bessel function of the first kind[9]. A(k) will be expressed by the MM expansion functions.. The electric field components are given by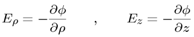 | (5) |
2.3. MM Equation Based on Expansion Functions Defined in the Infinite Domain
- Expanding Eρ outside the disk, on the disk plane, by the MM set of expansion functions {ej(ρ), j = 1,2,..N} where N is the number of expansion functions taken to the calculation, we have
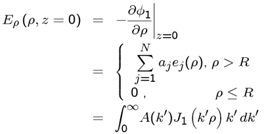 | (5) |
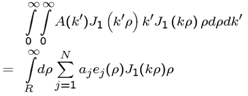 | (7) |
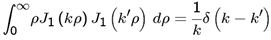 | (8) |
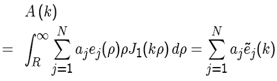 | (9) |
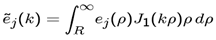 | (10) |
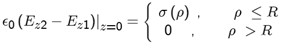 | (11) |
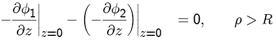 | (12) |
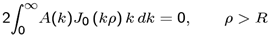 | (13) |
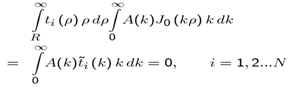 | (14) |
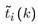 is given by
is given by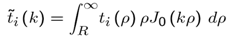 | (15) |
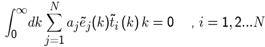 | (16) |
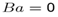 | (17) |
2.3. MM Equation Based on Expansion Functions Defined in the Finite Domain
- In this case we expand the surface charge density
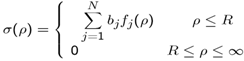 | (19) |
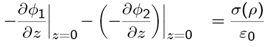 | (20) |
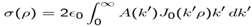 | (21) |
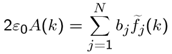 | (22) |
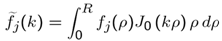 | (23) |
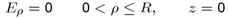 | (24) |
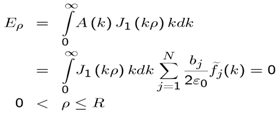 | (25) |
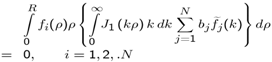 | (26) |
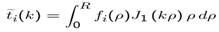 | (27) |
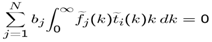 | (28) |
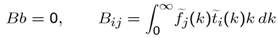 | (29) |
2.4. Choosing the Expansion Functions in the Infinite Domain
- The expansion functions for Eρ (ρ, z = 0) are chosen such to obey the physical behaviour of this field component near the edge of the disk and at infinity. The behaviour is given by
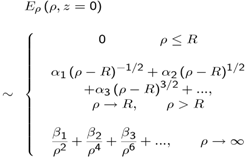 | (30) |
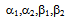 are constants. It can be shown that the following functions belonging to the two sets below for Eρ
are constants. It can be shown that the following functions belonging to the two sets below for Eρ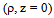
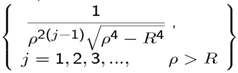 | (31) |
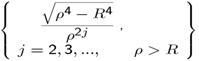 | (32) |
2.5. Choosing the Expansion Functions in the Finite Domain
- The a-priory physical behaviour if the surface charge density known to us is
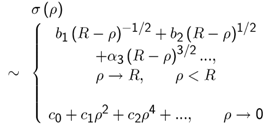 | (33) |
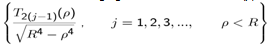 | (34) |
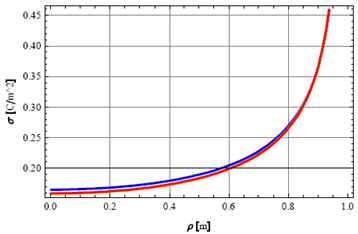
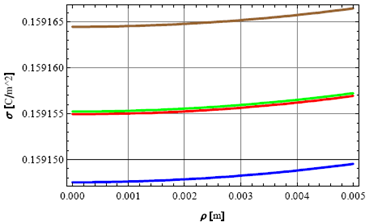
3. Numerical Results
3.1 MM Solution Based on Expansion Functions Defined in the Infinite Domain
- The expansion functions taken for the calculation were
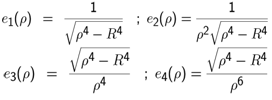 | (35) |
|
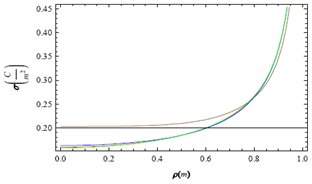
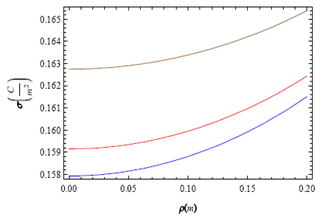
3.2. MM Solution Based on Expansion Functions Defined in the Finite Domain
- The three expansion functions fi (ρ), i = 1, 2, 3 for the surface charge density on the disk taken to the calculation were, respectively
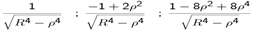 | (36) |
|
4. Conclusions
- The possibility to apply the moment method by using expansion functions describing the fields in the infinite domain (outside the body) has been checked, and it is shown that excellent accuracy and converging rate has been achieved, even slightly better than the case of the conventional MM solution based on expansion functions defined on the finite body. The key point was the requirement that the expansion functions will exactly obey the a-priori known physical behavior of the fields, near the edge of the body and at infinity. We conclude that efficient MM solutions based on expansion functions defined in an infinite domain is possible. The efficiency of the MM solution based on expansion functions defined in the infinite domain has to be checked in the future for electromagnetic problems, for example for antennas with different electrical sizes.
Appendix
A1. The Fourier-Bessel Transform of the 1st expansion Function Defined in the Infinite Domain
- The Fourier-Bessel transform for the MM first expansion function in the infinite domain is
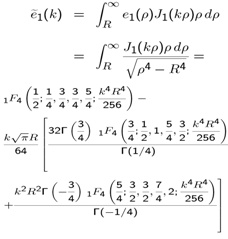 | (A1) |
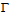 is the gamma functions[14].
is the gamma functions[14].A2. Calculation the behaviour of the potential around the disk for ρ→∞
- A calculation for finding the behaviour of the potential at infinity is shown below[15].
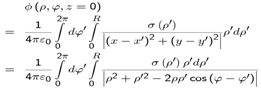 | (A2) |
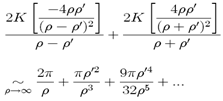 | (A4) |
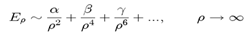 | (A5) |
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML