-
Paper Information
- Next Paper
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Computational and Applied Mathematics
p-ISSN: 2165-8935 e-ISSN: 2165-8943
2012; 2(2): 42-48
doi: 10.5923/j.ajcam.20120202.08
Further Results on the Effects of Variable Viscosity and Magnetic Field on Flow and Heat Transfer to a Continuous Flat Plate in the Presence of Heat Generation and Radiation with a Convective Boundary Condition
Olanrewaju P. O 1, Anake T 1, Arulogun O. T 2, Ajadi D. A. 3
1Department of Mathematics, Covenant University, Ota, Nigeria
2Department of Computer Science and Technology, Ladoke Akintola University of Technology, Ogbomoso
3Department of Pure and Applied Physics, Ladoke Akintola University of Technology, Ogbomoso
Correspondence to: Olanrewaju P. O , Department of Mathematics, Covenant University, Ota, Nigeria.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
The steady, laminar boundary layer flow with a convective boundary condition, to a continuously moving flat plate is studied taking into account the variation of viscosity with temperature in the presence of a magnetic field, heat generation and thermal radiation. The fluid viscosity is assumed to vary as a linear function of temperature. The resulting, governing equations are non-dimensionalized and transformed using a similarity transformation and then solved numerically by sixth order Runge-Kutta method alongside with shooting method. Comparison with previously published work is performed and there was a perfect agreement at large value of the Biot number. A parametric study of all the embedded flow parameters involved is conducted, and a representative set of numerical results for the velocity and temperature profiles as well as the skin-friction parameter and the Nusselt number is illustrated graphically to show typical trend of the solutions. It is worth pointing out that, when the variation of viscosity with temperature is strong in the presence of the effect of a magnetic field, radiation, heat generation, the results of the present work are completely different from those that studied the same problem in the absence of magnetic field, thermal radiation and the heat generation. It is interesting to note that higher the values of Prandtl number lesser the effects of Biot number and the magnetic field intensity.
Keywords: Variable Viscosity, Heat Transfer, Convective Boundary Condition, Heat Generation, Thermal Radiation
Article Outline
1. Introduction
- Fluid flow and heat transfer through porous medium have been of considerable interest, especially in the past decade. This is primarily because of numerous applications of flow through porous media, such as storage of radioactive nuclear waste materials transfer, separation processes in chemical industries, filtration, thermal insulation engineering, packed- bed reactors, transpiration cooling, transport processes in aquifers, ground water pollution etc. This topic is of vital importance in all these applications, thereby generating the need for a full understanding of transport processes through porous media. Theories and experiments of thermal convection in porous media and state-of-the-art reviews, with special emphasis on practical applications have been presented in the recent books by Nield and Bejan[1], Ingham and Pop[2], Vafai[3], Pop and Ingham[4] and Bejan et al.[5]. The problem of natural convection heat transfer with constant viscosity from a vertical plate in a saturated porous medium is discussed in references[6-7].The fundamental analysis of convection through porous media with temperature dependent viscosity is driven by several contemporary engineering applications from cooling of electronic devices to porous journal bearings and it is important for studying the variations in constitutive property. The effects of variable viscosity for convective heat transfer through porous media are studied by several investigators (Lai and Kulacki[8], Kumari[9],) etc. Seddeek and Salem[10] obtained further results on the effects of variable viscosity with magnetic field on flow and heat transfer to a continuous moving flat plate. Jayanthi and Kumari[11] examined the effects of variable viscosity on non-Darcy free or mixed convection flow on a vertical surface in a fluid saturated porous medium. Chin et al.[12] investigated the effects of variable viscosity on mixed convection boundary layer flow over a vertical surface embedded in a porous medium.The heat-transfer analysis of boundary-layer flows with radiation is also important in electrical power generation, astrophysical flows, solar power technology, space vehicle re-entry and other industrial areas. Extensive literature that deals with flows in the presence of radiation effects abounds. Raptis et al.[13] studied the effect of thermal radiation on the magnetohydrodynamic flow of a viscous fluid past a semi-infinite stationary plate. Hayat et al.[14] extended the analysis of reference[13] for a second-grade fluid.Convective heat transfer studies are very important in processes involving high temperatures, such as gas turbines, nuclear plants and thermal energy storage. Recently, Ishak[15] examined the similarity solutions for flow and heat transfer over a permeable surface with convective boundary condition. Moreover, Aziz[16] studied a similarity solution for laminar thermal boundary layer over a flat plate with a convective surface boundary condition. Very recently, Olanrewaju, et al.[17] examined the effects of internal heat generation, thermal radiation and buoyancy force on a boundary layer over a vertical plate with a convective surface boundary condition.The objective of this present paper was to explore the effects of thermal radiation and internal heat generation on the variable viscous fluid under a convective surface boundary condition which is an extension of Seddeek and Salem[10] and Pop et al.[18]. No study appeared to have considered the combined effects of thermal radiation and internal heat generation with a convective heat exchange at the plate surface on the boundary layer flow, which is the focus of this paper. The non-linear equations governing the flow were solved numerically using a shooting technique together with a sixth-order Runge-Kutta integration scheme. Pertinent results are displayed graphically and discussed quantitatively.
2. Mathematical Formulation
- We consider the steady state, laminar flow of a viscous, incompressible fluid over a moving plate placed in a calm environment with u and v denoting, respectively, the velocity components in the x and y direction. A magnetic field of strength B(x) is considered to be applied parallel to y-direction, which is normal to the plate. Here, it is assumed that the induced magnetic field produced by the motion of an electrically conducting fluid is negligible. It is also further assumed that the fluid properties are isotropic and constant, except for the fluid viscosity, which is assumed to vary as inverse linear function of temperature given by[10]:
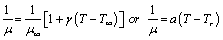 Where
Where 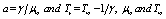 are the fluid free stream dynamic viscosity and the fluid free stream temperature, a and Tr are constants and their values depend on the reference state and the thermal property of the fluid
are the fluid free stream dynamic viscosity and the fluid free stream temperature, a and Tr are constants and their values depend on the reference state and the thermal property of the fluid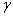 . In general, a > 0 for liquids and a < 0 for gases. Under the above assumption, the boundary layer equations including variable viscosity, thermal radiation, internal heat generation and magnetic field are as follows.
. In general, a > 0 for liquids and a < 0 for gases. Under the above assumption, the boundary layer equations including variable viscosity, thermal radiation, internal heat generation and magnetic field are as follows.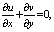 | (1) |
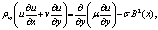 | (2) |
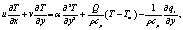 | (3) |
 is the ambient fluid density, σ is the electrical conductivity, α is the thermal diffusivity, Q is the heat release per unit volume, cp is the heat capacity at constant temperature, and qr is the radiative flux, respectively.The boundary conditions associated with Eqs. (1)-(3) are as follows:
is the ambient fluid density, σ is the electrical conductivity, α is the thermal diffusivity, Q is the heat release per unit volume, cp is the heat capacity at constant temperature, and qr is the radiative flux, respectively.The boundary conditions associated with Eqs. (1)-(3) are as follows: | (4) |
 | (5) |
 | (6) |
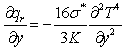 | (7) |
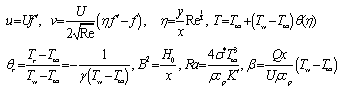 | (8) |
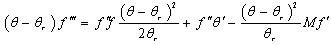 | (9) |
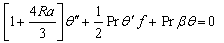 | (10) |
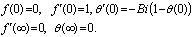 | (11) |
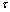 ) and the Nusselt number (Nu) can be easily computed. These quantities are defined in dimensionless terms as:
) and the Nusselt number (Nu) can be easily computed. These quantities are defined in dimensionless terms as: 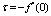 and
and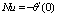 .
.3. Numerical Procedure
- The set of non-linear ordinary differential equations (9)–(10) with boundary conditions in (11) have been solved numerically by using the Runge–Kutta integration scheme with a modified version of the Newton–Raphson shooting method with Ra,θr M, Bi and Pr as prescribed parameters. A similarity solution for the momentum and the thermal boundary layer equations is possible if the convective heat transfer of the fluid heating the plate on its left surface is proportional to
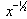 . The computations were done by a program which uses a symbolic and computational computer language MAPLE[20]. A step size of ∆f = 0.001 was selected to be satisfactory for a convergence criterion of 10-10 in nearly all cases. The value of y∞ was found to each iteration loop by the assignment statement η∞ = η∞ +. The maximum value of η∞, to each group of parameters Ra, θr, M, Bi and Pr is determined when the values of unknown boundary conditions at η = 0 do not change to successful loop with error less than 10-10.
. The computations were done by a program which uses a symbolic and computational computer language MAPLE[20]. A step size of ∆f = 0.001 was selected to be satisfactory for a convergence criterion of 10-10 in nearly all cases. The value of y∞ was found to each iteration loop by the assignment statement η∞ = η∞ +. The maximum value of η∞, to each group of parameters Ra, θr, M, Bi and Pr is determined when the values of unknown boundary conditions at η = 0 do not change to successful loop with error less than 10-10.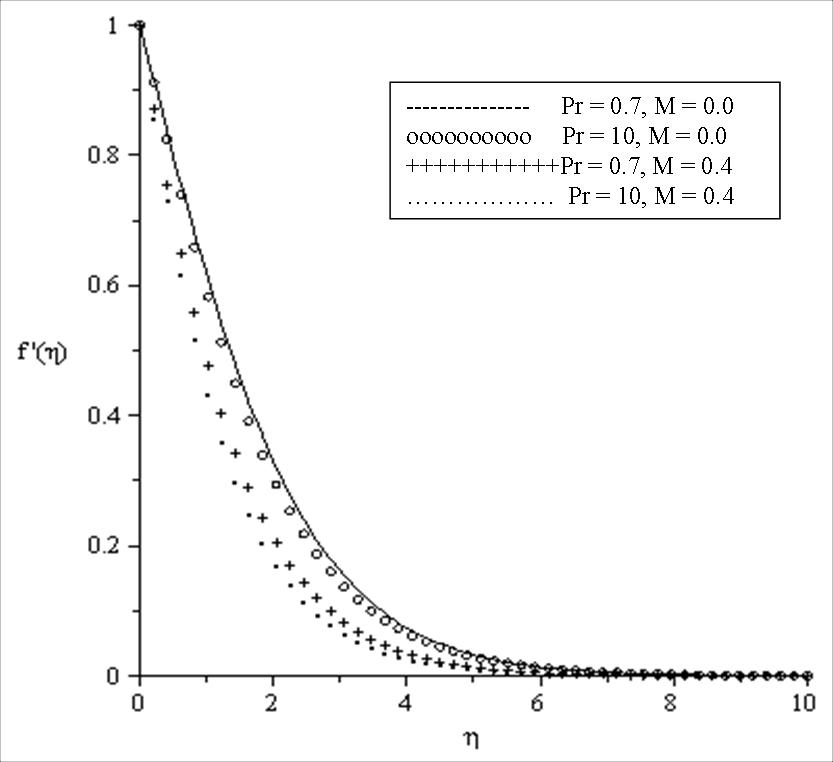 | Figure 1. Effects of Pr and M on the velocity profiles for fixed values of Bi = 0.1, β = 0.1, Ra = 0.1, θr = 2 |
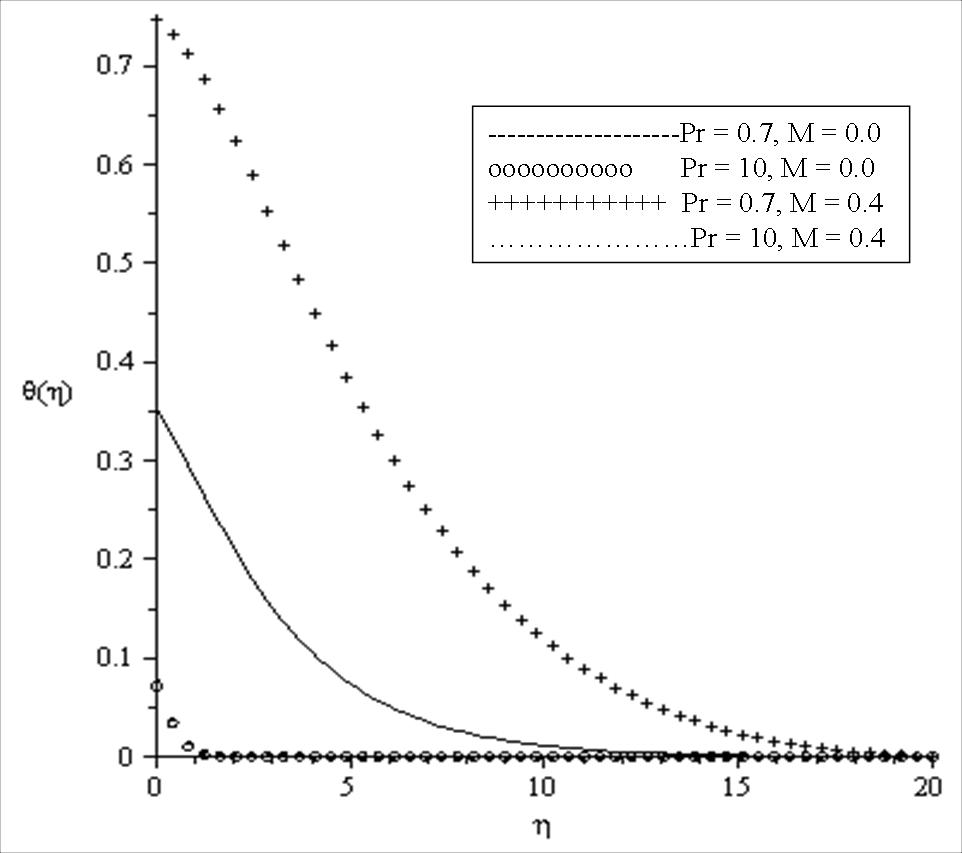 | Figure 2. Effects of Pr and M on the temperature profiles for fixed values of Bi = 0.1, β = 0.1, Ra = 0.1, θr = 2 |
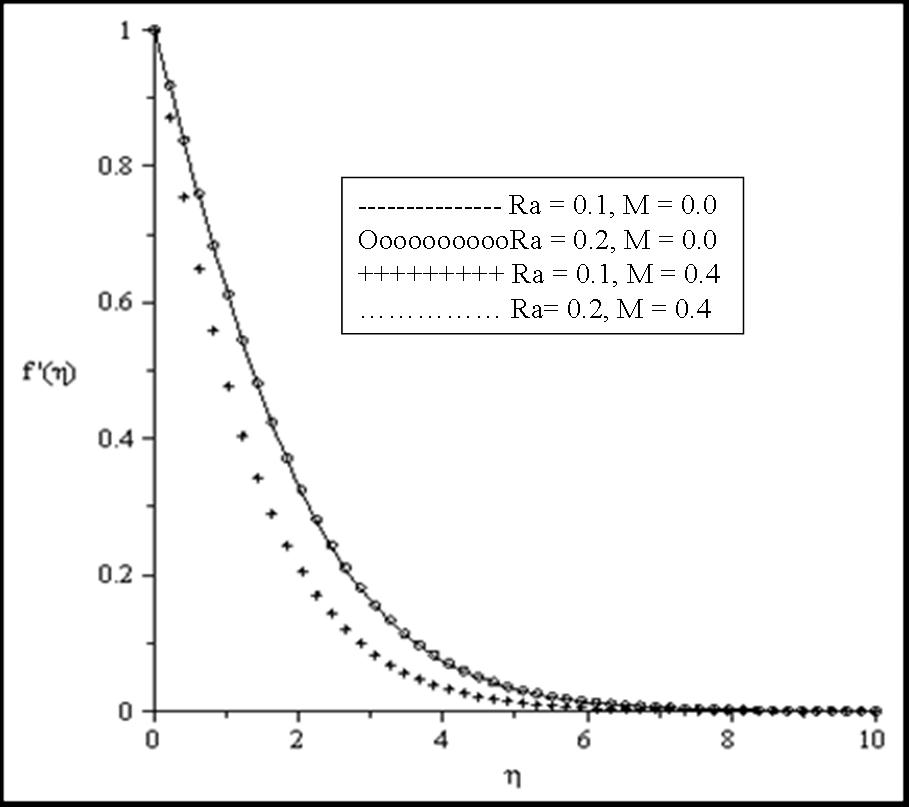 | Figure 3. Effects of Ra and M on the velocity profiles for fixed values of Bi = 0.1, β = 0.1, Pr = 0.7, θr = 2 |
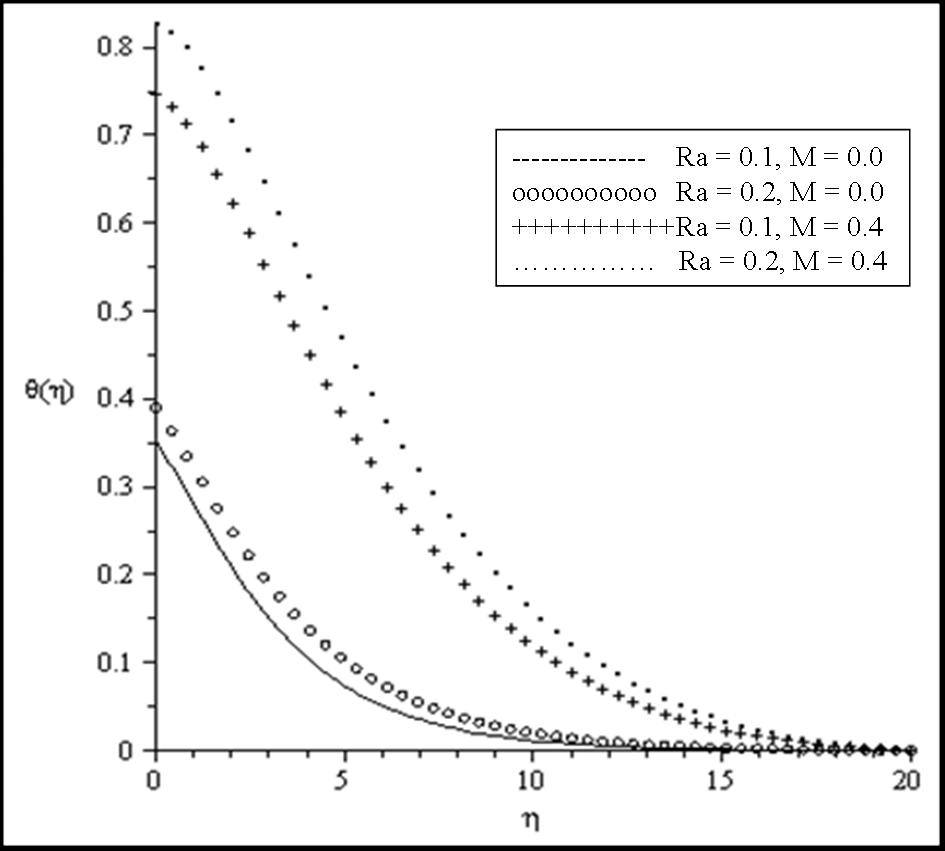 | Figure 4. Effects of Ra and M on the temperature profiles for fixed values of Bi = 0.1, β = 0.1, Pr = 0.7, θr = 2 |
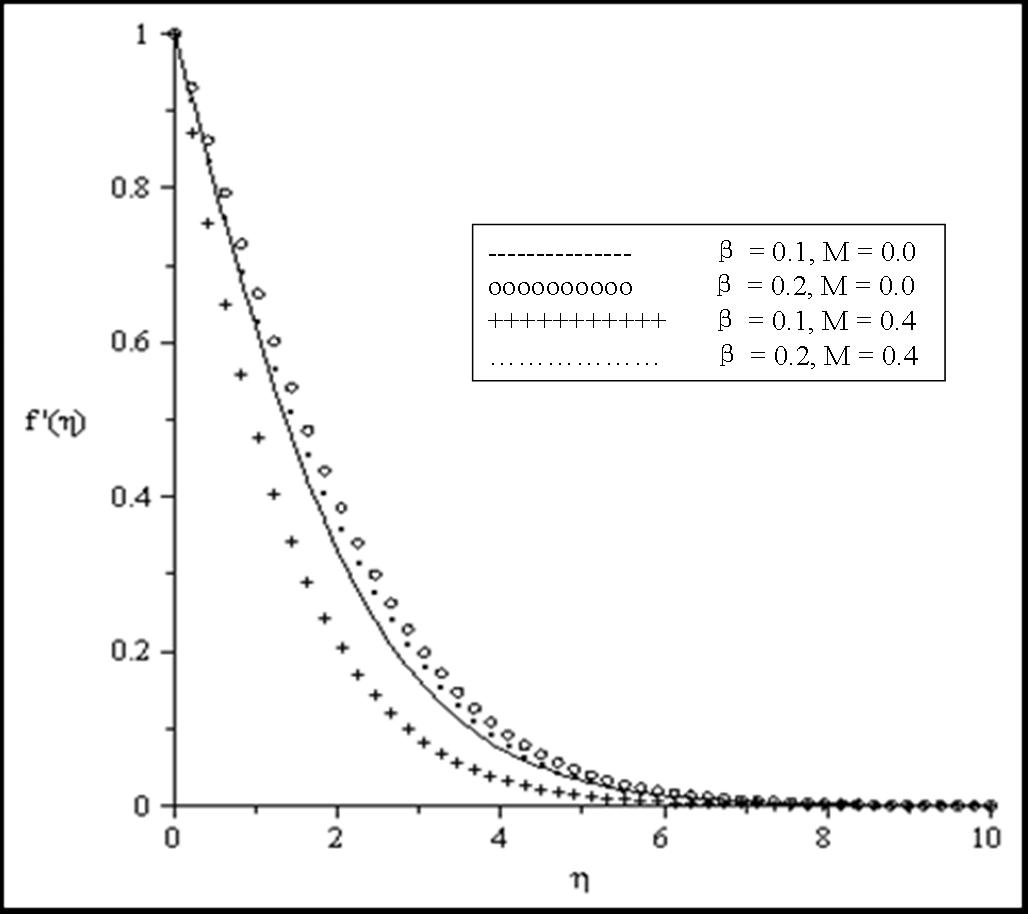 | Figure 5. Effects of β and M on the velocity profiles for fixed values of Bi = 0.1, Ra = 0.1, Pr = 0.7, θr = 2 |
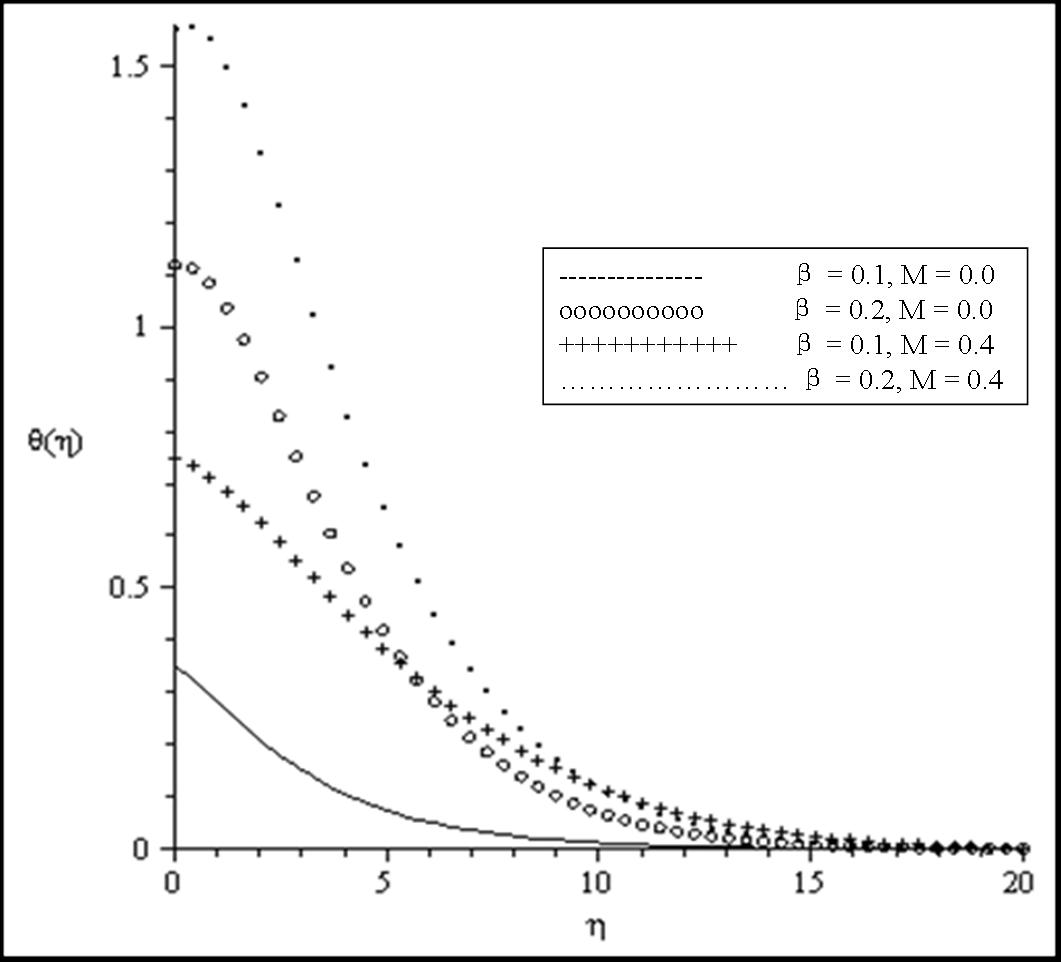 | Figure 6. Effects of β and M on the temperature profiles for fixed values of Bi = 0.1, Ra = 0.1, Pr = 0.7, θr = 2 |
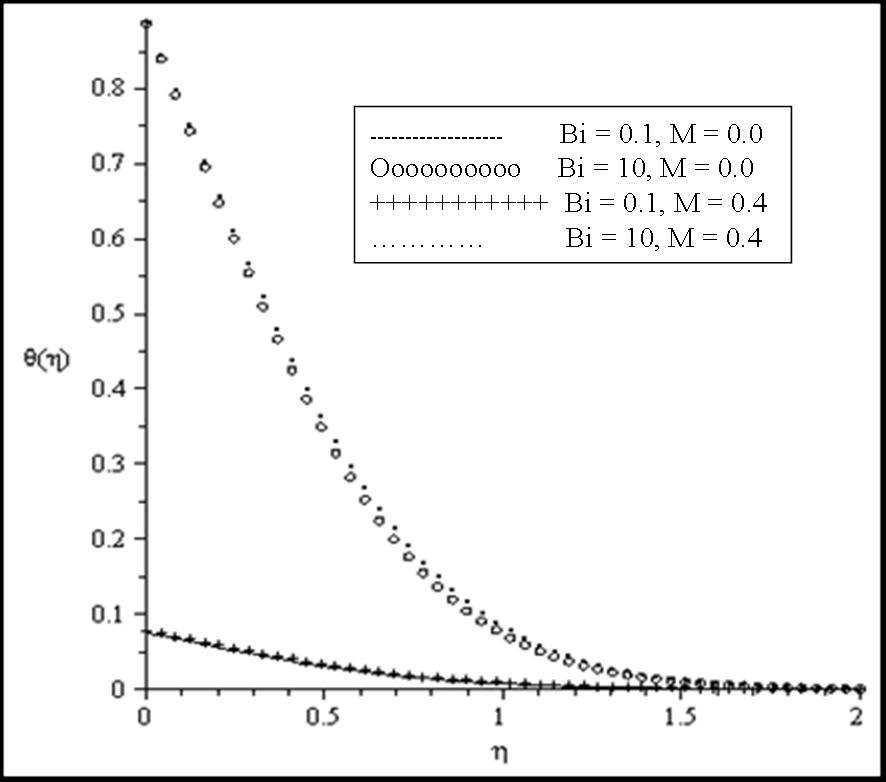 | Figure 7. Effects of Bi and M on the temperature profiles for fixed values of β = 0.1, Ra = 0.1, Pr = 10, θr = 2 |
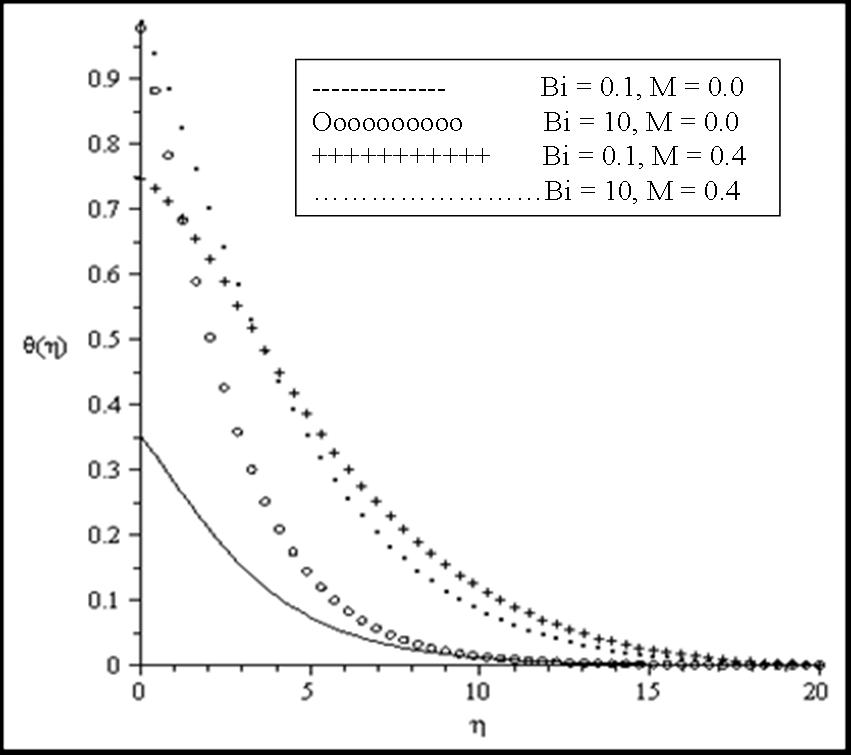 | Figure 8. Effects of Bi and M on the temperature profiles for fixed values of β = 0.1, Ra = 0.1, Pr = 0.7, θr = 2 |
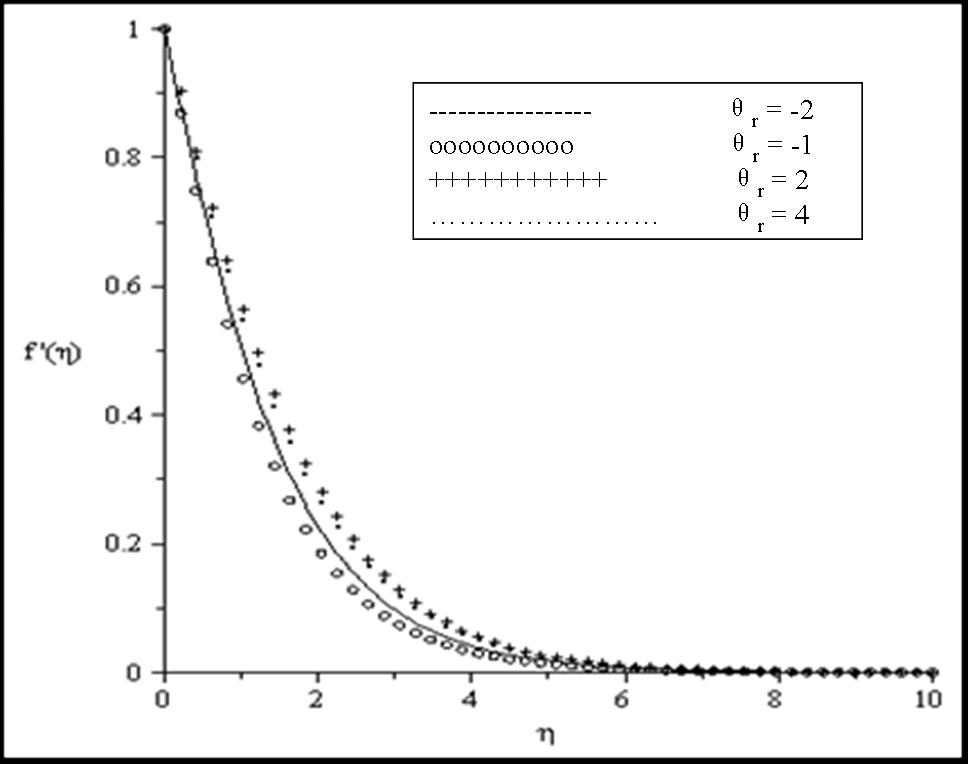 | Figure 9. Effects of θr on the concentration profiles when Bi = 0.1, Ra = 0.1, Pr = 0.7, β = 0.1, M = 0.1 |
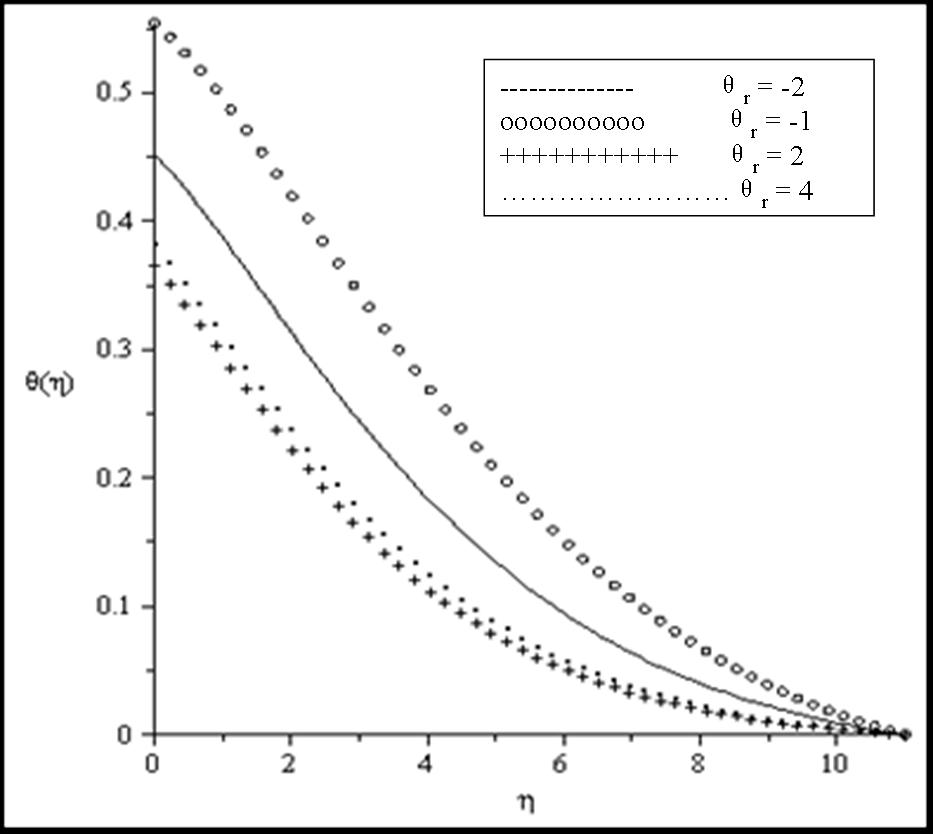 | Figure 10. Effects of θr on the temperature profiles when Bi = 0.1, Ra = 0.1, Pr = 0.7, β = 0.1, M = 0.1 |
4. Results and Discussion
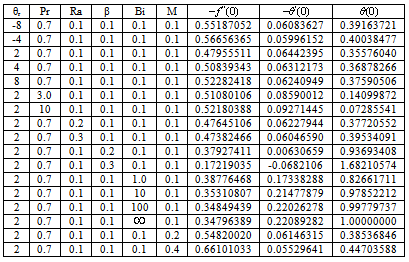
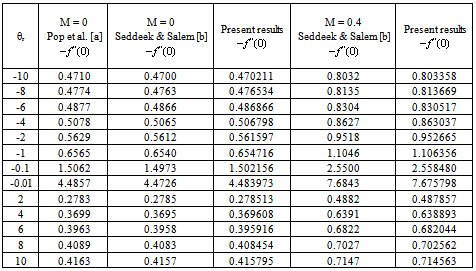
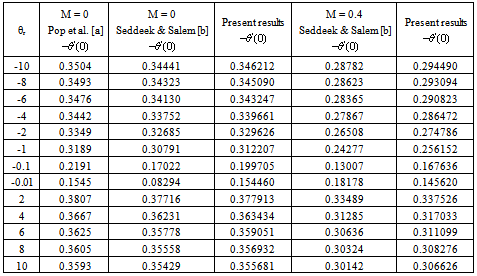
- In order to get a clear insight of the physical problem, the velocity and temperature have been discussed by assigning numerical values to the parameters encountered in the problem. To be realistic, the values of Prandtl number is chosen to be Pr = 0.7 which represents air at temperature 25oC and one atmospheric pressure. Attention is focused on the presence of magnetic field, thermal radiation and the internal heat generation parameters, respectively. Tables 1 and 2 show perfect agreement with the existing literature for with and without the presence of magnetic field strength parameter to assess the accuracy. It can also be mentioned that, when
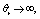 the fluid viscosity becomes equal to ambient viscosity, and we have the classical Sakiadis problem. From Table 3, it should be noted that increasing Prandtl number and magnetic field parameter leads to an increase in the skin friction coefficient while increasing radiation parameter Ra, internal heat generation parameter β and Biot number Bi reduces the skin friction coefficient at the wall surface. It is interesting to note that increasing θr, Ra, β, Bi and M enhances the wall surface temperature. Similarly, decreasing Ra, β and M enhances the heat transfer rate at the surface while increasing Pr and Bi enhances the heat transfer rate. Here, it is clear that the effect of internal heat generation β, thermal radiation Ra, magnetic field intensity M and the convective heat transfer Bi is well pronounced. To reveal the influence of the embedded flow parameters on the flow and temperature fields, the velocity and temperature distribution are shown in Figures 1-10. Figures 1 and 2 illustrate the influence of ambient Prandtl number Pr and magnetic field parameter M on the velocity and temperature profiles in the boundary layer, respectively. It should be noted that increasing Prandtl number and magnetic field parameter thins the velocity boundary layer thickness which establishes the influence of the magnetic parameter to an electrically conducting fluid gives rise to a resistive-type force called the Lorentz force. This force has the tendency to slow down the motion of the fluid in the boundary layer and to increase its temperature (see figures 1-2). Effects of the thermal radiation Ra and the magnetic field M on the velocity and the temperature profiles were displayed in Figures 3 and 4. Increasing the radiation and magnetic parameters enhances the heat transfer rate while the velocity boundary layer thickness decreases. It was observed that increasing the internal heat generation and magnetic field parameter enhances the thermal and velocity boundary layer thickness (see Figures 5-6). It is noteworthy to mention here that when the ambient Prandtl number is 0.7, the convective heat transfer Bi has profound influence on the thermal boundary layer thickness that when the ambient Prandtl number is 10 (see Figures 7-8). Figures 9-10 discuses the effects of θr on the velocity and thermal boundary layer thickness. As θr increases positively, the velocity boundary layer thickness increases, while it thins the thermal boundary layer thickness.
the fluid viscosity becomes equal to ambient viscosity, and we have the classical Sakiadis problem. From Table 3, it should be noted that increasing Prandtl number and magnetic field parameter leads to an increase in the skin friction coefficient while increasing radiation parameter Ra, internal heat generation parameter β and Biot number Bi reduces the skin friction coefficient at the wall surface. It is interesting to note that increasing θr, Ra, β, Bi and M enhances the wall surface temperature. Similarly, decreasing Ra, β and M enhances the heat transfer rate at the surface while increasing Pr and Bi enhances the heat transfer rate. Here, it is clear that the effect of internal heat generation β, thermal radiation Ra, magnetic field intensity M and the convective heat transfer Bi is well pronounced. To reveal the influence of the embedded flow parameters on the flow and temperature fields, the velocity and temperature distribution are shown in Figures 1-10. Figures 1 and 2 illustrate the influence of ambient Prandtl number Pr and magnetic field parameter M on the velocity and temperature profiles in the boundary layer, respectively. It should be noted that increasing Prandtl number and magnetic field parameter thins the velocity boundary layer thickness which establishes the influence of the magnetic parameter to an electrically conducting fluid gives rise to a resistive-type force called the Lorentz force. This force has the tendency to slow down the motion of the fluid in the boundary layer and to increase its temperature (see figures 1-2). Effects of the thermal radiation Ra and the magnetic field M on the velocity and the temperature profiles were displayed in Figures 3 and 4. Increasing the radiation and magnetic parameters enhances the heat transfer rate while the velocity boundary layer thickness decreases. It was observed that increasing the internal heat generation and magnetic field parameter enhances the thermal and velocity boundary layer thickness (see Figures 5-6). It is noteworthy to mention here that when the ambient Prandtl number is 0.7, the convective heat transfer Bi has profound influence on the thermal boundary layer thickness that when the ambient Prandtl number is 10 (see Figures 7-8). Figures 9-10 discuses the effects of θr on the velocity and thermal boundary layer thickness. As θr increases positively, the velocity boundary layer thickness increases, while it thins the thermal boundary layer thickness.
|
|
|
5. Conclusions
- Further results on the effects of variable viscosity and magnetic field on flow and heat transfer to a continuous flat plate in the presence of heat generation and radiation with a convective surface boundary condition were obtained numerically. The problem is formulated in such a way that the viscosity of the fluid varied inversely as a linear function of the temperature. The transformed equations are solved numerically using sixth order Runge-Kutta method alongside with shooting method. We have quantitatively compared our results with those of Seddeek and Salem[10] and Pop et al.[18], and the agreement between both results is excellent. The numerical results are influenced by magnetic field, internal heat generation, thermal radiation and the convective heat transfer compared with the existing results. It is also found that the changes of the thermal boundary layer thickness with the change of Biot number, radiation and internal heat generation when the ambient Prandtl number is equal to 0.7 compared with Pr = 10. A similarity solution for the momentum and the thermal boundary layer equations is possible if the convective heat transfer of the fluid heating the plate on its left surface is proportional to
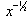 .
.ACKNOWLEDGEMENTS
- Dr. Olanrewaju want to thank the financial assistance of Covenant University, Ota, Nigeria.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML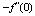 for Pr = 0.7, Ra = 0, β = 0,
for Pr = 0.7, Ra = 0, β = 0, 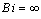
 for Pr = 0.7, Ra = 0, β = 0,
for Pr = 0.7, Ra = 0, β = 0, 
 for various values of Pr, Ra, β, θr, M and Bi
for various values of Pr, Ra, β, θr, M and Bi