Yogesh Gupta , Manoj Kumar
Department of Mathematics, Motilal Nehru National Institute of Technology, Allahabad 211004, (U.P.) India
Correspondence to: Yogesh Gupta , Department of Mathematics, Motilal Nehru National Institute of Technology, Allahabad 211004, (U.P.) India.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
In the present paper, a numerical algorithm using fifth degree quintic B-spline for fourth order singular perturbation problem has been developed. The most of the numerical methods used for higher order singularly perturbed boundary value problems transform the problems into equivalent system of first and/or second order differential equations. However, in the present method, fifth degree B-spline is applied directly to the problem without transforming the problem into an equivalent system. The method uses values of fifth degree B-spline function and its derivatives up to the order four at nodal points. Resulting system of equations is solved to get the required quintic B-spline solution. Since perturbed problems contain boundary layers, the strategy of fitted mesh is used which assigns more mesh points in the boundary layer regions. The algorithm is tested on two problems to demonstrate the practical usefulness and superiority of the approach.
Keywords:
Singularly Perturbed Boundary Value Problems, Quintic B-Spline, Mesh Points
1. Introduction
Singularly perturbed boundary value problems are encountered in various fields such as solid mechanics, quantum mechanics, optimal control, chemical reactor theory, aerodynamics, reaction-diffusion processes, geophysics, etc. Higher-order singularly perturbed boundary value problems have important applications in fluid dynamics. Singularly perturbed higher order problems are classified on the basis that how the order of the original differential equation is affected if one sets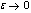 , here
, here 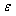 is a small positive parameter multiplying the highest derivative of the differential equation. We say that the singular perturbation problem (SPP) is of convection-diffusion type if the order of the differential equations is reduced by one, whereas it is called reaction-diffusion type if the order is reduced by two.The analytical treatment of singularly perturbed boundary value problems (SPBVPs) for the higher order differential equations had been discussed by Feckan[3], Howes[7] and Nayfeh[9]. In the past two decades a large number of publications have appeared on numerical methods which cover mostly second order singularly perturbed boundary value problems Gupta et al.[6], Kumar et al.[8]) and system of perturbed problems (Gupta et al.[5], Valanarasu et al.[15]); but only few authors have developed numerical methods for singularly perturbed higher order differential equations. Niederdrenk and Yserentant[10] considered convection- diffusion type problems and derived conditions for the uniform stability of discrete and continuous problems. Gartlend[4] has shown that uniform stability of the discrete BVP follows from uniform stability of the discrete initial value problem and uniform consistency of the scheme. Some results connected with the exponentially fitted higher order differences with identity expansion method (Gartlend[4]) and defect corrections are available in the literature. Feckan[3] considered higher order problems and his approach is based on the non-linear analysis involving fixed point theory, Leray- Schauder theory, etc. Numerical methods for fourth order SPBVPs are also considered by Chuanhan[2] and Ramanujam et al.[12]. Shanti et al.[14] considered a SPBVP for fourth order equations of the type
is a small positive parameter multiplying the highest derivative of the differential equation. We say that the singular perturbation problem (SPP) is of convection-diffusion type if the order of the differential equations is reduced by one, whereas it is called reaction-diffusion type if the order is reduced by two.The analytical treatment of singularly perturbed boundary value problems (SPBVPs) for the higher order differential equations had been discussed by Feckan[3], Howes[7] and Nayfeh[9]. In the past two decades a large number of publications have appeared on numerical methods which cover mostly second order singularly perturbed boundary value problems Gupta et al.[6], Kumar et al.[8]) and system of perturbed problems (Gupta et al.[5], Valanarasu et al.[15]); but only few authors have developed numerical methods for singularly perturbed higher order differential equations. Niederdrenk and Yserentant[10] considered convection- diffusion type problems and derived conditions for the uniform stability of discrete and continuous problems. Gartlend[4] has shown that uniform stability of the discrete BVP follows from uniform stability of the discrete initial value problem and uniform consistency of the scheme. Some results connected with the exponentially fitted higher order differences with identity expansion method (Gartlend[4]) and defect corrections are available in the literature. Feckan[3] considered higher order problems and his approach is based on the non-linear analysis involving fixed point theory, Leray- Schauder theory, etc. Numerical methods for fourth order SPBVPs are also considered by Chuanhan[2] and Ramanujam et al.[12]. Shanti et al.[14] considered a SPBVP for fourth order equations of the type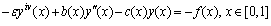 | (1) |
subject to the boundary conditions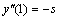 | (2) |
here ε > 0 is a small positive parameter, b(x), c(x) and f(x) are sufficiently smooth functions and 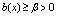 . The fundamental idea used by them is that of the boundary value technique (BVT) after transforming the fourth order SPBVP into an equivalent system of two second order BVPs.The objective of the present paper is to develop a computational method using quintic B-spline to solve singularly perturbed boundary value problems for fourth order equations of the type (1)-(2) directly without transforming the problem into an equivalent system of lower order differential equations. The remaining components of the paper are organized as follows- In Section 2, numerical method for concerned problem is developed after presenting the definition of quintic B-spline and a table for values of derivatives up to fourth order at nodes. Section 3 contains mesh selection procedure for boundary layers. In Section 4, numerical validations of the developed algorithm are included to compare and demonstrate the efficiency of the method, which shows that the present algorithm performs better than some existing methods for the similar problems.
. The fundamental idea used by them is that of the boundary value technique (BVT) after transforming the fourth order SPBVP into an equivalent system of two second order BVPs.The objective of the present paper is to develop a computational method using quintic B-spline to solve singularly perturbed boundary value problems for fourth order equations of the type (1)-(2) directly without transforming the problem into an equivalent system of lower order differential equations. The remaining components of the paper are organized as follows- In Section 2, numerical method for concerned problem is developed after presenting the definition of quintic B-spline and a table for values of derivatives up to fourth order at nodes. Section 3 contains mesh selection procedure for boundary layers. In Section 4, numerical validations of the developed algorithm are included to compare and demonstrate the efficiency of the method, which shows that the present algorithm performs better than some existing methods for the similar problems.
2. Quintic B-Spline Collocation Method
Consider equally spaced knots of a partition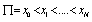 , such that
, such that 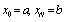 on[a,b]. Let
on[a,b]. Let 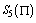 be the space of continuously-differentiable, piecewise, fifth-degree polynomials on
be the space of continuously-differentiable, piecewise, fifth-degree polynomials on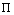 , that is,
, that is, 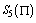 is the space of fifth-degree splines on
is the space of fifth-degree splines on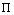 . The definition and description of quintic B-spline functions generated by subdivision has been explained by Prenter[11] and Caglar et al.[1]. Consider the B-spline basis in
. The definition and description of quintic B-spline functions generated by subdivision has been explained by Prenter[11] and Caglar et al.[1]. Consider the B-spline basis in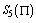 defined as
defined as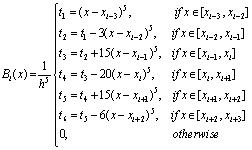 | (3) |
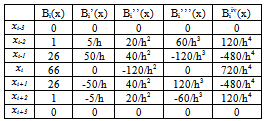
To solve fourth order boundary value problem, 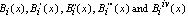 evaluated at the nodal points are needed. Their coefficients are summarized in Table 1:
evaluated at the nodal points are needed. Their coefficients are summarized in Table 1:Table 1. Values of
 and and
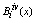 at Nodal Points at Nodal Points
 |
| |
|
Let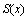 be the B-spline interpolating the function
be the B-spline interpolating the function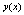 at the nodal points and
at the nodal points and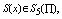 then we have
then we have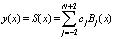 | (4) |
Also, let the approximate solution of given BVP (1) is given by (4), where 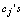 are unknown coefficients and
are unknown coefficients and ’s fifth degree B-Spline functions.Now, this approximate solution must satisfy the given BVP at the nodal points
’s fifth degree B-Spline functions.Now, this approximate solution must satisfy the given BVP at the nodal points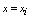 . For, putting values from (4) in (1), we get
. For, putting values from (4) in (1), we get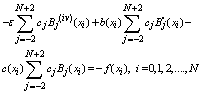 | (5) |
and boundary conditions give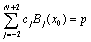 | (6) |
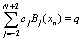 | (7) |
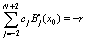 | (8) |
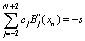 | (9) |
The values of spline functions and derivatives at the knots are determined using Table 1 and substituting these in (5)-(9), a system of N+5 linear equations in N+5 unknowns is obtained, which can be solved to get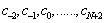 and in turn, the quintic B-spline solution.
and in turn, the quintic B-spline solution.
3. Mesh Selection for Boundary Layers
In this section, we construct the piecewise uniform mesh in such a way that more mesh points are generated in the boundary layer regions than outside these regions. Let the given interval be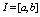 and it is divided into N subintervals where N =2r with r ≥ 3. We follow the mesh selection procedure according to the presence of boundary layers at both ends of the interval, at the left end of the interval and at the right end of the interval in the given singularly perturbed boundary value problem[13].Since boundary layers are present at both ends for the considered fourth order singularly perturbed boundary value problems, we divide interval
and it is divided into N subintervals where N =2r with r ≥ 3. We follow the mesh selection procedure according to the presence of boundary layers at both ends of the interval, at the left end of the interval and at the right end of the interval in the given singularly perturbed boundary value problem[13].Since boundary layers are present at both ends for the considered fourth order singularly perturbed boundary value problems, we divide interval  into three parts
into three parts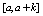 ,
, 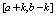 and
and 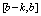 , where k is transition parameter given by
, where k is transition parameter given by 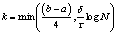 , where
, where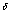 is width of the boundary layer and
is width of the boundary layer and 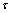 is a parameter defined according to the presence of the boundary layers. Now, we divide and each into N/4 equal mesh elements and into N/2 equal mesh elements. The resulting piecewise uniform mesh may be represented as
is a parameter defined according to the presence of the boundary layers. Now, we divide and each into N/4 equal mesh elements and into N/2 equal mesh elements. The resulting piecewise uniform mesh may be represented as 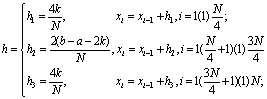 | (10) |
4. Numerical Examples
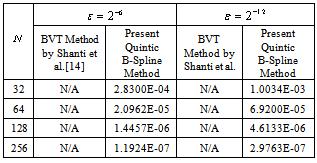
In this section, we consider two numerical examples illustrating the comparative performance of quintic B-spline collocation method over other methods for similar problems.Example 1. Consider the following fourth order singularly perturbed boundary value problemwith the boundary conditionsThe point wise errors for 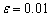 by present method are compared with that of boundary value technique by Shanti et al.[14] in following Table 2, which demonstrates that present algorithm gives better results. However, we have also presented maximum absolute errors by our algorithm in Table 3 for various values of and N.Example 2. Consider the following singularly perturbed boundary value problemwith the boundary conditionsThe maximum absolute errors for various values of N and
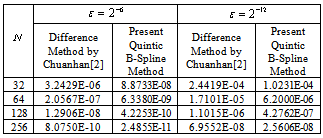
by present method are compared with that of boundary value technique by Shanti et al.[14] in following Table 2, which demonstrates that present algorithm gives better results. However, we have also presented maximum absolute errors by our algorithm in Table 3 for various values of and N.Example 2. Consider the following singularly perturbed boundary value problemwith the boundary conditionsThe maximum absolute errors for various values of N and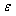 by present algorithm for Example 2 are compared with that of difference method by Liu Chuanhan[2] in Table 4, which shows that present algorithm performs better.
by present algorithm for Example 2 are compared with that of difference method by Liu Chuanhan[2] in Table 4, which shows that present algorithm performs better.| Table 2. Point Wise Errors for Solution of Example 1 |
| | x | Error in Solution | | BVT Method by Shanti et al.[14] | Present Quintic B-Spline | | 0.0000 | 0.000000E-00 | 0.000000E-00 | | 0.0005 | 2.352183E-05 | 7.631670E-09 | | 0.0010 | 4.705214E-05 | 1.006600E-08 | | 0.0050 | 2.349982E-04 | 1.176580E-08 | | 0.0100 | 4.699924E-04 | 1.222000E-08 | | 0.0150 | 7.050314E-04 | 1.222000E-08 | | 0.0200 | 9.399432E-04 | 1.624511E-08 | | 0.0250 | 1.175027E-03 | 1.624902E-08 | | 0.0300 | 1.409955E-03 | 3.381042E-08 | | 0.2180 | 1.410139E-03 | 1.192400E-07 | | 0.4060 | 1.410016E-03 | 1.190100E-07 | | 0.5940 | 1.410015E-03 | 1.186500E-07 | | 0.7820 | 1.410136E-03 | 1.190000E-07 | | 0.8760 | 1.410730E-03 | 1.183300E-07 | | 0.9700 | 1.409952E-03 | 3.381042E-08 | | 0.9750 | 1.175024E-03 | 1.631950E-08 | | 0.9800 | 9.399410E-04 | 1.624000E-08 | | 0.9850 | 7.050297E-04 | 1.243300E-08 | | 0.9900 | 4.699913E-04 | 1.237930E-08 | | 0.9950 | 2.349976E-04 | 1.212000E-08 | | 0.9990 | 4.705203E-05 | 1.006643E-08 | | 0.9995 | 2.352178E-05 | 7.445600E-09 | | 1.0000 | 0.000000E-00 | 0.000000E-00 |
|
|
Table 3. Max. Absolute Errors for Solution of Example 1
 |
| |
|
Table 4. Max. Absolute Errors for Solution of Example 2
 |
| |
|
5. Conclusions
In this paper, a numerical algorithm is developed using quintic B-spline for singularly perturbed fourth order boundary value problem. The developed method employs fifth degree B-spline to fourth order problem without reducing it into equivalent system of lower order differential equations. To handle the boundary layers, we have used the mesh selection procedure in which more points are kept in boundary layer regions. The results presented in Table 3 and Table 4 establish that the present method is almost fourth order convergent. Also, the results obtained by the present algorithm are better than those produced by other stated methods for similar problems.
References
| [1] | Caglar H., Caglar N., Ozer M., Fifth-degree B-spline solution for nonlinear fourth order problems with separated boundary conditions, Journal of Physics: Conference Series, 96 (2008), 012031. |
| [2] | Chuanhan Liu, Fourth-order accurate difference method for the singular perturbation problem, Applied Mathematics and Mechanics, 18(10) (1997), 987-995. |
| [3] | Feckan M, Singularly perturbed higher order boundary value problems, Journal of Differential Equations, 3 (1) (1994), 79-102. |
| [4] | Gartlend E.C., Graded-mesh difference schemes for singularly perturbed two-point boundary value problems, Mathematics of Computation, 51 (1988), 631-657. |
| [5] | Gupta Y., Kumar M., Srivastava P.K., Application of B-spline to numerical solution of a system of singularly perturbed boundary value problems, Mathematica Aeterna, 1(6) (2011), 405-415. |
| [6] | Gupta Y., Kumar M., Anthology of spline based numerical techniques for singularly perturbed boundary value problems, International Journal of Pure and Applied Mathematics 74 (4) (2012), 437-453. |
| [7] | Howes F.A., Differential inequalities of higher order and the asymptotic solution of nonlinear boundary value problems, SIAM Journal on Mathematical Analysis, 13 (1) (1982), 61-80. |
| [8] | Kumar M., Singh P., Mishra H. K., A recent survey on computational techniques for solving singularly perturbed boundary value problems, International Journal of Computer Mathematics, 84 (2007), 1439-1463. |
| [9] | Nayfeh A.H., Introduction to perturbation methods, (1981) Wiley, New York. |
| [10] | Niederdrenk K., Yserentant H., The uniform stability of singularly perturbed discrete and continuous boundary value problems, Numerische Mathematik, 41 (1983), 223-253. |
| [11] | Prenter P.M., Splines and variational methods, (1989) Wiley. |
| [12] | Ramanujam N., Shanthi V., Computational methods for reaction-diffusion problems for fourth-order ordinary differential equations with a small parameter at the highest derivative, Applied Mathematics and Computation, 147 (2004), 97-113. |
| [13] | Rao S.C.S., Kumar M., B-spline collocation method for nonlinear singularly perturbed two-point boundary value problems, Journal of Optimization Theory and Applications, 134 (2007), 91-105. |
| [14] | Shanthi V., Ramanujam N., A numerical method for boundary value problems for singularly perturbed fourth order ordinary differential equations, Applied Mathematics and Computation, 129 (2002), 269-294. |
| [15] | Valanarasu T., Ramanujam N., An asymptotic initial value method for boundary value problems for a system of singularly perturbed second order ordinary differential equations, Applied Mathematics and Computation, 147 (2004), 227-240. |
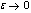 , here
, here 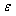 is a small positive parameter multiplying the highest derivative of the differential equation. We say that the singular perturbation problem (SPP) is of convection-diffusion type if the order of the differential equations is reduced by one, whereas it is called reaction-diffusion type if the order is reduced by two.The analytical treatment of singularly perturbed boundary value problems (SPBVPs) for the higher order differential equations had been discussed by Feckan[3], Howes[7] and Nayfeh[9]. In the past two decades a large number of publications have appeared on numerical methods which cover mostly second order singularly perturbed boundary value problems Gupta et al.[6], Kumar et al.[8]) and system of perturbed problems (Gupta et al.[5], Valanarasu et al.[15]); but only few authors have developed numerical methods for singularly perturbed higher order differential equations. Niederdrenk and Yserentant[10] considered convection- diffusion type problems and derived conditions for the uniform stability of discrete and continuous problems. Gartlend[4] has shown that uniform stability of the discrete BVP follows from uniform stability of the discrete initial value problem and uniform consistency of the scheme. Some results connected with the exponentially fitted higher order differences with identity expansion method (Gartlend[4]) and defect corrections are available in the literature. Feckan[3] considered higher order problems and his approach is based on the non-linear analysis involving fixed point theory, Leray- Schauder theory, etc. Numerical methods for fourth order SPBVPs are also considered by Chuanhan[2] and Ramanujam et al.[12]. Shanti et al.[14] considered a SPBVP for fourth order equations of the type
is a small positive parameter multiplying the highest derivative of the differential equation. We say that the singular perturbation problem (SPP) is of convection-diffusion type if the order of the differential equations is reduced by one, whereas it is called reaction-diffusion type if the order is reduced by two.The analytical treatment of singularly perturbed boundary value problems (SPBVPs) for the higher order differential equations had been discussed by Feckan[3], Howes[7] and Nayfeh[9]. In the past two decades a large number of publications have appeared on numerical methods which cover mostly second order singularly perturbed boundary value problems Gupta et al.[6], Kumar et al.[8]) and system of perturbed problems (Gupta et al.[5], Valanarasu et al.[15]); but only few authors have developed numerical methods for singularly perturbed higher order differential equations. Niederdrenk and Yserentant[10] considered convection- diffusion type problems and derived conditions for the uniform stability of discrete and continuous problems. Gartlend[4] has shown that uniform stability of the discrete BVP follows from uniform stability of the discrete initial value problem and uniform consistency of the scheme. Some results connected with the exponentially fitted higher order differences with identity expansion method (Gartlend[4]) and defect corrections are available in the literature. Feckan[3] considered higher order problems and his approach is based on the non-linear analysis involving fixed point theory, Leray- Schauder theory, etc. Numerical methods for fourth order SPBVPs are also considered by Chuanhan[2] and Ramanujam et al.[12]. Shanti et al.[14] considered a SPBVP for fourth order equations of the type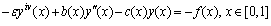
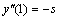
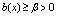 . The fundamental idea used by them is that of the boundary value technique (BVT) after transforming the fourth order SPBVP into an equivalent system of two second order BVPs.The objective of the present paper is to develop a computational method using quintic B-spline to solve singularly perturbed boundary value problems for fourth order equations of the type (1)-(2) directly without transforming the problem into an equivalent system of lower order differential equations. The remaining components of the paper are organized as follows- In Section 2, numerical method for concerned problem is developed after presenting the definition of quintic B-spline and a table for values of derivatives up to fourth order at nodes. Section 3 contains mesh selection procedure for boundary layers. In Section 4, numerical validations of the developed algorithm are included to compare and demonstrate the efficiency of the method, which shows that the present algorithm performs better than some existing methods for the similar problems.
. The fundamental idea used by them is that of the boundary value technique (BVT) after transforming the fourth order SPBVP into an equivalent system of two second order BVPs.The objective of the present paper is to develop a computational method using quintic B-spline to solve singularly perturbed boundary value problems for fourth order equations of the type (1)-(2) directly without transforming the problem into an equivalent system of lower order differential equations. The remaining components of the paper are organized as follows- In Section 2, numerical method for concerned problem is developed after presenting the definition of quintic B-spline and a table for values of derivatives up to fourth order at nodes. Section 3 contains mesh selection procedure for boundary layers. In Section 4, numerical validations of the developed algorithm are included to compare and demonstrate the efficiency of the method, which shows that the present algorithm performs better than some existing methods for the similar problems.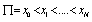 , such that
, such that 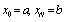 on[a,b]. Let
on[a,b]. Let 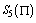 be the space of continuously-differentiable, piecewise, fifth-degree polynomials on
be the space of continuously-differentiable, piecewise, fifth-degree polynomials on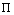 , that is,
, that is, 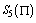 is the space of fifth-degree splines on
is the space of fifth-degree splines on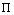 . The definition and description of quintic B-spline functions generated by subdivision has been explained by Prenter[11] and Caglar et al.[1]. Consider the B-spline basis in
. The definition and description of quintic B-spline functions generated by subdivision has been explained by Prenter[11] and Caglar et al.[1]. Consider the B-spline basis in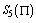 defined as
defined as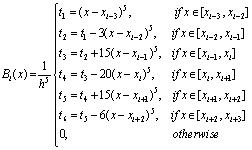
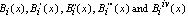 evaluated at the nodal points are needed. Their coefficients are summarized in Table 1:
evaluated at the nodal points are needed. Their coefficients are summarized in Table 1: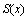 be the B-spline interpolating the function
be the B-spline interpolating the function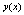 at the nodal points and
at the nodal points and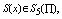 then we have
then we have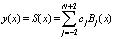
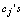 are unknown coefficients and
are unknown coefficients and ’s fifth degree B-Spline functions.Now, this approximate solution must satisfy the given BVP at the nodal points
’s fifth degree B-Spline functions.Now, this approximate solution must satisfy the given BVP at the nodal points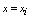 . For, putting values from (4) in (1), we get
. For, putting values from (4) in (1), we get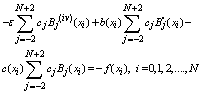
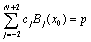
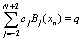
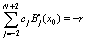
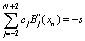
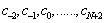 and in turn, the quintic B-spline solution.
and in turn, the quintic B-spline solution.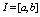 and it is divided into N subintervals where N =2r with r ≥ 3. We follow the mesh selection procedure according to the presence of boundary layers at both ends of the interval, at the left end of the interval and at the right end of the interval in the given singularly perturbed boundary value problem[13].Since boundary layers are present at both ends for the considered fourth order singularly perturbed boundary value problems, we divide interval
and it is divided into N subintervals where N =2r with r ≥ 3. We follow the mesh selection procedure according to the presence of boundary layers at both ends of the interval, at the left end of the interval and at the right end of the interval in the given singularly perturbed boundary value problem[13].Since boundary layers are present at both ends for the considered fourth order singularly perturbed boundary value problems, we divide interval 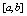 into three parts
into three parts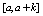 ,
, 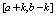 and
and 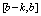 , where k is transition parameter given by
, where k is transition parameter given by 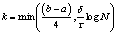 , where
, where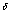 is width of the boundary layer and
is width of the boundary layer and 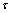 is a parameter defined according to the presence of the boundary layers. Now, we divide and each into N/4 equal mesh elements and into N/2 equal mesh elements. The resulting piecewise uniform mesh may be represented as
is a parameter defined according to the presence of the boundary layers. Now, we divide and each into N/4 equal mesh elements and into N/2 equal mesh elements. The resulting piecewise uniform mesh may be represented as 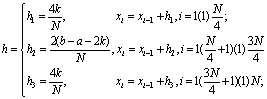
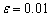 by present method are compared with that of boundary value technique by Shanti et al.[14] in following Table 2, which demonstrates that present algorithm gives better results. However, we have also presented maximum absolute errors by our algorithm in Table 3 for various values of and N.Example 2. Consider the following singularly perturbed boundary value problemwith the boundary conditionsThe maximum absolute errors for various values of N and
by present method are compared with that of boundary value technique by Shanti et al.[14] in following Table 2, which demonstrates that present algorithm gives better results. However, we have also presented maximum absolute errors by our algorithm in Table 3 for various values of and N.Example 2. Consider the following singularly perturbed boundary value problemwith the boundary conditionsThe maximum absolute errors for various values of N and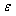 by present algorithm for Example 2 are compared with that of difference method by Liu Chuanhan[2] in Table 4, which shows that present algorithm performs better.
by present algorithm for Example 2 are compared with that of difference method by Liu Chuanhan[2] in Table 4, which shows that present algorithm performs better. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML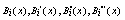 and
and 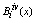 at Nodal Points
at Nodal Points 

