Stefan A. Pape , Tzvetalin S. Vassilev
Department of Computer Science and Mathematics, Nipissing University, North Bay, Ontario, P1B 8L7, Canada
Correspondence to: Tzvetalin S. Vassilev , Department of Computer Science and Mathematics, Nipissing University, North Bay, Ontario, P1B 8L7, Canada.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
We consider the problem of finding the staircase kernel in orthogonal polygons, with or without holes, in the plane. Orthogonal polygon is a simple polygon in the plane whose sides are either horizontal or vertical. We generalize the notion of visibility in the following way: We say that two points a and b in an orthogonal polygon P are visible to each other via staircase paths if and only if there exist an orthogonal chain connecting a and b and lying entirely in the interior of P. Furthermore, the orthogonal chain should have the property that the angles between the consecutive segments in the chain are either or , and these should alternate along the chain. There are two principal types of staircases, NW-SE and NE-SW. The notion of staircase visibility has been studied in the literature for the last three decades. Based on this notion we can generalize the notion of star-shapedness. A polygon P is called star-shaped under staircase visibility, or simply s-star if and only if there is nonempty set of points S in the interior of P, such that any point of S sees any point of P via staircase path. The largest such set of points is called the staircase kernel of P and denoted ker P. Our work is motivated by the work of Breen [1]. She proves that the staircase kernel of an orthogonal polygon without holes is the intersection of all maximal orthogonally convex polygons contained in it. We extend Breen's results for the case when the orthogonal polygon has holes. We prove the necessary geometric properties, and use them to derive a quadratic time, O() algorithm for computing the staircase kernel of an orthogonal polygon with holes, having n vertices in total, including the holes' vertices. The algorithm is based on the plane sweep technique, widely used in Computational Geometry[4]. Our result is optimal in the case of orthogonal polygon with holes, since the kernel (as proven) can consist of quadratic number of disjoint regions. In the case of polygon without holes, there is a linear time algorithm by Gewali[3], that is specific to the case of a polygon without holes. We present examples of our algorithm's results.
Keywords:
Orthogonal Polygon, Staircase Visibility, Staircase Kernel
1. Introduction
The problem of visibility in a polygon has been considered in Computational Geometry over the last four decades. The well-known Art Gallery Problem and its variations are the most prominent examples of visibility problems. To begin, consider a simply connected polygon P in the plane, P is convex if for every point q in P, q is visible from each other point in P. By introducing the notion that P is non-convex, this becomes no longer possible. P is non-convex if there exist points p and q in P such that p is not visible from q via a line segment that lies entirely in the interior of P. Thus not all pairs of points in P have direct visibility. The notion of non-convexity also provides the possibility that P is star-shaped. A polygon P is star-shaped, if there exists a point p such that for each point q in P the line segment pq lies entirely within P. Since there exists such a point p we want to find the core set of p, the set of all such points that see all other points in P. The core set of all points p will be referred to as the kernel of P. The kernel of a polygon is the intersection of all its interior half-planes, an algorithm to find the kernel was constructed to run in O(n) time. However not all polygons are star-shaped, so a generalization is needed. Fortunately, a simple thing to generalize is the notion of visibility. A path in 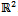 from point p to point q is referred to as an orthogonal path or orthogonal chain if its edges are parallel to the coordinate axes and alternate in direction, and thus p “sees” q. As it can be seen in Figure 2, any simply connected orthogonal polygon is convex in terms of visibility by orthogonal paths. Further refinement of the concept is the introduction of the notion of staircase paths. An orthogonal path is called a staircase path, if the turns along the path alternate between +90° and−90°. A polygon P is star-shaped via staircase paths if there is a point p in P that sees every other point of P via staircase paths.We now introduce the concept of orthogonal polygons (rectilinear polygon). A polygon P in the plane is orthogonal if its edges are parallel to the coordinate axes, thus its edges meet at right-angles, and the interior angle at each vertex is either 90° or 270°.
from point p to point q is referred to as an orthogonal path or orthogonal chain if its edges are parallel to the coordinate axes and alternate in direction, and thus p “sees” q. As it can be seen in Figure 2, any simply connected orthogonal polygon is convex in terms of visibility by orthogonal paths. Further refinement of the concept is the introduction of the notion of staircase paths. An orthogonal path is called a staircase path, if the turns along the path alternate between +90° and−90°. A polygon P is star-shaped via staircase paths if there is a point p in P that sees every other point of P via staircase paths.We now introduce the concept of orthogonal polygons (rectilinear polygon). A polygon P in the plane is orthogonal if its edges are parallel to the coordinate axes, thus its edges meet at right-angles, and the interior angle at each vertex is either 90° or 270°.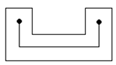 | Figure 1. Star-shaped polygon under the definition of staircase visibility |
1.1. Theorem 1
Any simple orthogonal polygon P is convex with respect to orthogonal paths.Proof: Choose any points p,q in P. Since P is a simple orthogonal polygon its edges are parallel to the coordinate axes, and its interior is simply connected. Then an orthogonal path can be drawn from p to q. Then p “sees” q, and under the definition of orthogonal visibility each point of P is visible from every other point, and thus P is convex with respect to orthogonal paths.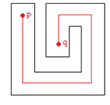 | Figure 2. A polygon that is convex via orthogonal paths |
Now consider the restriction that an orthogonal path can only travel North West/South East or North East/South West. This restriction does not guarantee that every orthogonal polygon is convex. Refer to the polygon in Figure 1, the two given points are not visible to each other via staircase path. However, a question now arises, is the orthogonal polygon star-shaped? Is there a point p that sees all other points via staircase paths? This gives rise to the question of our research, how to find the core sets of all such points p, which will be referred to as the staircase kernel of P.
2. Geometric Preliminaries
There have been several papers on the subject of staircase visibility and orthogonal polygons. Much of the material considered is from Dr. Marilyn Breen's publications. Breen's approach follows from a well-known argument that for a polygon P that is star-shaped via line segments, the convex kernel of P is the intersection of all maximal convex subsets of P. What is shown in[1] is that for P, a simply connected orthogonal polygon that is star-shaped via staircase paths, the staircase kernel of P is the intersection of all maximal orthogonally convex polygons in P, which is itself an orthogonally convex polygon. Breen uses the following lemmas to prove this case. Refer to[1] for the proofs and the full proof of Theorem 2 [1, Theorem 1].Lemma 1: If P is an orthogonal polygon, then P contains finitely many maximal orthogonal convex polygons. Moreover, every orthogonally convex polygon in P lies in a maximal orthogonally convex polygon in P. Lemma 2: Let x, y, z be points in P, and let λ 1, λ 2, λ 3 be staircase paths joining x to y, y to z, and x to z respectively. Then the bounded region T determined by λ=λ1∪λ2∪λ3 is an orthogonally convex polygon.
2.1. Theorem 2
[1, Theorem 1] Let P be a simply connected orthogonal polygon which is star-shaped via staircase paths. Then (1) the staircase kernel of P is the intersection of all maximal orthogonal convex polygons in P and (2) it is again an orthogonally convex polygon.Proof: Let ker P refer to the staircase kernel of P, and P be a simply connected polygon in the plane.(1) Let M denote the family of all maximal orthogonally convex polygons in P. By Lemma 1, M is finite and as such every orthogonally convex polygon in P lies in a member of M. It will be shown that the ker P = ∩ { m : m ∈ M}Choose any point x in ∩ { m : m ∈ M}, and let y be any point in P. Then some member m0 of M contains y, so x, y∈ m0. By [2, Lemma 1], there is an orthogonally convex polygon in P containing x and y if and only if there is a staircase path in P from x to y. Hence x sees y via a staircase path, x ∈ ker P, and ∩{ m : m ∈M} ⊆ ker P.(2) To show that ker P is an orthogonally convex polygon, it is shown that the ker P is connected. Let x, y ∈ ker P, and let λ 1 be any staircase path in P from x to y, to show that λ 1⊆ ker P. That is for w ∈ λ 1 and z ∈P, show that w sees z via a staircase path in P. Since x, y ∈ ker P, there are staircase paths λ2, λ3 in P from y to z, and x to z, respectively. Then by Lemma 2, the bounded region T determined by λ1∪λ2∪λ3 is an orthogonally convex polygon. Hence, by [2 Lemma 1], every two points of T are joined by a staircase path in T. Moreover since P is simply connected, T ⊆ P, so every two points of T are joined by a staircase path in P. Thus for w ∈ λ1, w sees z via a staircase path in P, λ1⊆ ker P, and ker P is indeed connected.Since ker P is a connected intersection of finitely many orthogonally convex polygons, ker P is an orthogonally convex polygon.While Breen's approach is sound, it is not constructive enough for our purposes. By analysing the proof, we can find a way to construct an algorithm for the problem in question. Theorem 2 considers an orthogonal polygon that is already known to be star-shaped via staircase paths, so we will consider the converse of Theorem 2.
2.2. ConverseTheorem 2
Let P be a simply connected orthogonal polygon in . If P is a union of maximal orthogonally convex polygons which have a common intersection that is convex. Then P is star-shaped via staircase paths.Proof: Let ker P refer to the staircase kernel of P, and P be a simply connected polygon in the plane. Let M denote the family of all maximal orthogonally convex polygons in P, and let ker P = ∩ { m : m in M}. Choose any point x ∈ ker P, and y ∈ P. Then since y ∈ P, y ∈ m in M and since ker P = ∩ {m : m in M}, there is a staircase path λ from x to y since each m in M is convex. Thus for all x ∈ ker P, and y ∈ P, x sees y via staircase paths, and thus P is star-shaped.By analysing the converse we can observe that given an orthogonal polygon P in the plane, we can decompose P into maximal orthogonally convex polygons. Then their intersection will be the staircase kernel of P. In Figure 3, given P observe that the red and the blue polygons are the maximal orthogonally convex subpolygon decomposition of P, and their intersection yields the staircase kernel shown in green.
. If P is a union of maximal orthogonally convex polygons which have a common intersection that is convex. Then P is star-shaped via staircase paths.Proof: Let ker P refer to the staircase kernel of P, and P be a simply connected polygon in the plane. Let M denote the family of all maximal orthogonally convex polygons in P, and let ker P = ∩ { m : m in M}. Choose any point x ∈ ker P, and y ∈ P. Then since y ∈ P, y ∈ m in M and since ker P = ∩ {m : m in M}, there is a staircase path λ from x to y since each m in M is convex. Thus for all x ∈ ker P, and y ∈ P, x sees y via staircase paths, and thus P is star-shaped.By analysing the converse we can observe that given an orthogonal polygon P in the plane, we can decompose P into maximal orthogonally convex polygons. Then their intersection will be the staircase kernel of P. In Figure 3, given P observe that the red and the blue polygons are the maximal orthogonally convex subpolygon decomposition of P, and their intersection yields the staircase kernel shown in green.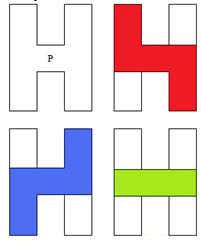 | Figure 3. Decomposition of P into maximal orthogonally convex sub-polygons, and its resulting kernel |
We can also observe from [1, Theorem 1] that if any maximal orthogonally convex polygon within P is not part of the intersection then P is not star-shaped. However, constructing an algorithmic approach that will efficiently decompose an orthogonal polygon into maximal orthogonally convex polygons is assumed to be of a high degree of time complexity, so we will consider another approach that will compute the staircase kernel of an orthogonal polygon.
3. Main Result
From Theorem 2 we know that the staircase kernel is an orthogonally convex polygon. So we will consider an algorithmic approach that given an orthogonal polygon P in the plane, will decompose P into parts, each will be an orthogonally convex polygon that is possibly not maximal. Since the staircase kernel is the set of all points that see each other point of P via staircase paths, each convex region must be verified to satisfy this property. Here we give an algorithm to compute the staircase kernel of any given orthogonal polygon in the plane. We have generalized the results of Breen as the algorithm has been constructed to also handle orthogonal polygons with holes. To begin, definitions of terms used, and lemmas are given.
3.1. Definitions
● Questionable Region: A region that is determined to be both horizontally and vertically convex.● Non-Visible Region: A region that cannot see another region via staircase paths.● Flagged Region: A region that is defined as either questionable or non-visible during a plane sweep.● Open Region: A region that is defined by an edge that enters the plane sweep or by an edge that is created to close an open region. Regions that are not simply connected are open.● Closed Region: An open region that has been closed by an edge, making it simply connected.
3.2. Lemmas
Lemma 1: During the plane sweep of a polygon P in , if a region is convex, then the following region is non-convex. The converse is also true.Lemma 2: During the plane sweep of a polygon P in
, if a region is convex, then the following region is non-convex. The converse is also true.Lemma 2: During the plane sweep of a polygon P in , while sweeping a non-convex region and a new edge enters the queue, if the edge is disjoint from the current regions, a new region is defined; else it is determined to be part of one of the current regions.Lemma 3: During the plane sweep of a polygon P in
, while sweeping a non-convex region and a new edge enters the queue, if the edge is disjoint from the current regions, a new region is defined; else it is determined to be part of one of the current regions.Lemma 3: During the plane sweep of a polygon P in , a region becomes closed if it encounters another defined region.Lemma 4: Regions within an orthogonal polygon P that are not vertically and horizontally convex are not part of the staircase kernel of P.Lemma 5: The intersections of horizontal convex regions with vertically convex regions within a polygon are horizontally and vertically convex.Lemma 6: The staircase kernel of a polygon P is vertically and horizontally convex [1, Theorem 1].Lemma 7: If there are multiple regions within a star-shaped polygon P that “see” every point in P via staircase paths, then the staircase kernel of P is disjoint.
, a region becomes closed if it encounters another defined region.Lemma 4: Regions within an orthogonal polygon P that are not vertically and horizontally convex are not part of the staircase kernel of P.Lemma 5: The intersections of horizontal convex regions with vertically convex regions within a polygon are horizontally and vertically convex.Lemma 6: The staircase kernel of a polygon P is vertically and horizontally convex [1, Theorem 1].Lemma 7: If there are multiple regions within a star-shaped polygon P that “see” every point in P via staircase paths, then the staircase kernel of P is disjoint.
3.3. Algorithm
Input: An orthogonal polygon P in 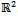 Output: The staircase kernel of P
Output: The staircase kernel of P
3.3.1. Part A: Search for Convex regions Within P
Step 1: Horizontal Plane Sweep, O(n)While sweeping P:● If an open region is closed while no other open regions are present, flag it as questionable.● If an open region is closed while one or more open regions are present, flag all regions currently part of the sweep as non-visible.● Place flagged regions top-down in the list Horizontal Convex Regions.While sweeping P, close an open region with an edge:● If two or more open regions meet.● If only one open region is present in the sweep and a disjoint edge enters the plane sweep.● If only two open regions are present in the sweep and one is closed.When a horizontal edge enters the plane sweep:● If no regions are present in the sweep, an open region is defined● If the edge is disjoint from any current region, an open region is defined● If the edge was created to close an open region, an open region is defined● If the edge is part of any current region, the sweep continues.Step 2: Vertical Plane Sweep, O(n)While sweeping P:● If an open region is closed while no other open regions are present, flag it as questionable.● If an open region is closed while one or more open regions are present, flag it as non-visible.● Place flagged regions top-down in the list Vertical Convex Regions.While sweeping P, close an open region with an edge:● If two or more open regions meet.● If only one open region is present in the sweep and a disjoint edge enters the plane sweep.● If only two open regions are present in the sweep and one is closed.When a vertical edge enters the plane sweep:● If no regions are present in the sweep, an open region is defined● If the edge is disjoint from any current region, an open region is defined● If the edge was created to close an open region, an open region is defined● If the edge is part of any current region, the sweep continues.Step 3: Intersect the questionable regions from both lists, O(n2)● Partition any questionable regions that become disjoint into the number of disjoint pieces● Update lists: Horizontal Convex Regions and Vertical Convex Regions
3.3.2. Part B: Check for Visibility
Step 1: Horizontal Convex Regions questionable region visibility check, O(n2)● Scan the list top-down● When a questionable region is found in the list, draw a staircase to each non-visible region before and after it in the list.● If successful, flag the region as H-visible and remove the region from the list● If unsuccessful, remove the region from the list● If no questionable regions remain, clear the listStep 2: Vertical Convex Regions questionable region visibility check, O(n2)● Scan the list top-down● When a questionable region is found in the list, draw a staircase to each non-visible region before and after it in the list.● If successful, flag the region as V-visible and remove the region from the list● If unsuccessful, remove the region from the list● If no questionable regions remain, clear the listStep 3: Determine the staircase kernel● A region is part of the staircase kernel if it is both H-visible and V-visible● If there are no regions that are both H-visible and V-visible, output is empty.
4. Analysis
4.1. Part A: Search for Convex Regions within P
4.1.1. Steps 1 and 2
The horizontal plane sweep of P follows from Lemmas 1 through 3. The plane sweep is meant to check the horizontal convexity of P. A convex region of P is defined as questionable since by [1, Theorem 1] the staircase kernel is horizontally and vertically convex, and non-convex regions are defined as non-visible since under the definition of staircase paths, no point in one region is visible from the points in any other defined as non-visible at an equivalent time. By Lemma 1 questionable regions are adjacent to non-visible regions, when a region is defined an edge is placed to close the region which divides the region from the next, the closed region is then placed into a list. So each region is defined by its closing edge, the closing edge is either a created edge or one that enters the plane sweep. Thus there are at most n defined regions placed into list which results in O(n) time. The vertical plane sweep behaves in the same manner as the horizontal plane sweep, thus also having a time complexity of O(n).
4.1.2. Step 3
To find the staircase kernel of P, we must consider regions within the polygon that are both vertically and horizontally convex, [1, Theorem 1]. Thus the intersection of horizontally convex regions and vertically convex regions must be found. The intersection follows from Lemmas 4 and 5. Any convex regions that do not intersect are discarded since they do not satisfy the properties of the kernel. To find the intersection, each questionable region in the Horizontal Convex Regions list has to be checked with each questionable regions in the Vertical Convex Regions list to determine if they intersect. This requires O(n2) time.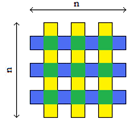 | Figure 4. O(n) vertical regions intersecting O(n) horizontal regions |
Figure 4 illustrates the case when the staircase kernel of an orthogonal polygon with holes has O(n2) complexity as there are O(n) vertical strips intersecting O(n) horizontal strips, thus there at most O(n2) intersections. Regions that become disjoint from the intersection are partitioned, and each partition is subject to further steps in the algorithm. The lists are updated as such; when the intersection of two or more questionable regions is found, the regions in both lists that correspond to the intersection are replaced with the intersection. The replacement regions will either be a smaller region maintaining the same number of regions in the lists, or be a group of partitions increasing the number of regions in the lists. Questionable regions that have non-empty intersections are removed from the lists, since by Lemma 6 will not be part of the staircase kernel; the removed items will in turn decrease the number of regions in the lists. Thus each questionable region in the updated lists corresponds to exactly one region in the other list, a one-to-one ratio. Updating the lists may increase or decrease the number of regions to check in later steps, but there will be still at most O(n) defined regions in the lists.
4.2. Part B: Check for visibility
4.2.1. Steps 1 and 2
Finding the kernel of P follows from Lemma 6. Since any point in the staircase kernel of P can see all points of P via staircases, a staircase path must be constructed from each questionable region in the lists to the non-visible regions in the list. If such a path cannot be constructed then the region does not satisfy the properties of the staircase kernel. As regions are checked they are determined as successful or failed and are removed from the list. When no questionable regions remain, then the list is cleared. Thus items enter the queue and are eventually removed. A staircase path can be constructed in O(n) time, as there are O(n) edges to traverse. With O(n) constructions in both lists, the time complexity of the visibility check is O(n2).
4.2.2. Step 3
Once the lists are cleared, the staircase kernel is the region that is successful in the Horizontal Convex Regions list and the Vertical Convex Regions list, since by [1, Theorem 1] the staircase kernel of P is horizontally and vertically convex, and under the definition of a staircase kernel sees each point in P. Thus if the output is non-empty then P is star-shaped via staircase paths. If no regions were successful in both lists, then there is no staircase kernel and as such P is not star-shaped. However, we find that with in the case that P has holes, Breens theorem, that the staircase kernel is in itself a convex orthogonal polygon no longer applies. Lemma 7 is a case where the kernel is disjoint and is as such non-convex. But each disjoint piece of the kernel is a convex orthogonal polygon and sees each point of P via staircase paths. Thus P still has a staircase kernel, and is star-shaped.The time complexity of the algorithm is O(n2) as argued in the analysis. The space complexity is also O(n2), since there might be as many as O(n2) regions in the kernel. The lists and the queue have linear complexity. The optimal time complexity to find the staircase kernel of an orthogonal polygon, possibly with holes is O(n2) as also proven by Laxmi P. Gewali [3, Theorem 6], refer to[3] for a different approach to the problem.
5. Examples
5.1. Example 1
Here we present an example of a simply connected orthogonal polygon P with no holes such that the algorithm will have a non-empty output.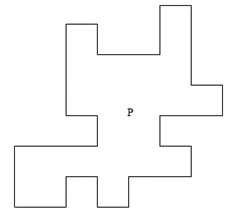 | Figure 5. An orthogonal polygon P |
Part A: Step 1 yields the Horizontal Convex Regions list, while Step 2 yields the Vertical Convex Regions list.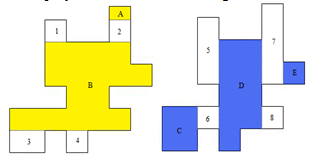 | Figure 6. Horizontal sweep and vertical sweep of P |
| Table 1. Sweep, the vertical and horizontal lists |
| | Horizontal Convex Regions | Vertical Convex Regions | | A | C | | 1 2 | 5 6 | | B | D | | 3 4 | 7 8 | | E |
|
|
Part A: Step 3 intersects the horizontal convex regions and the vertical convex regions to yield the updated lists containing regions that are both horizontally and vertically convex. Note that region B is partitioned into B1, B2, and B3, while region C and D are reduced in size. Since region A has an empty intersection it is removed from the lists.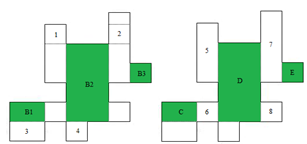 | Figure 7. Intersections of the horizontal and vertical convex regions |
| Table 2. The updated lists |
| | Horizontal Convex Regions | Vertical Convex Regions | | 1 2 | C | | B1 B2 B3 | 5 6 | | 3 4 | D | | 7 8 | | E |
|
|
Part B: Step 1 checks the staircase visibility of the questionable regions in the Horizontal Convex Regions list, and yields that region B2 is the only successful region.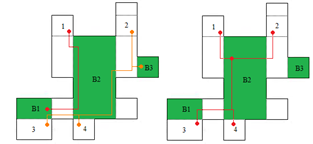 | Figure 8. Staircase visibility check of the horizontal convex regions |
| Table 3. Updated horizontal list after the visibility check |
| | Horizontal Convex Regions | | 1 2 | | B1(success) B2(success) B3(success) | | 3 4 |
|
|
Part B: Step 2 checks the staircase visibility of the questionable regions in the Vertical Convex Regions list, and yields that region D is the only successful region.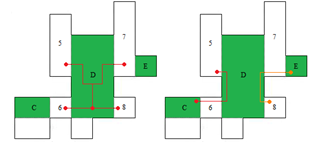 | Figure 9. Staircase visibility check of the vertical convex regions |
| Table 4. Updated vertical list after the visibility check |
| | Vertical Convex Regions | | C(fails) | | 5 6 | | D(success) | | 7 8 | | E(success) |
|
|
Part B: Step 3 finds that regions B2, and D were successful in the staircase visibility step. Since the regions in both lists correspond to each other, it is determined that the staircase kernel of P is the region defined by B2, and D. Thus P is star-shaped via staircase paths.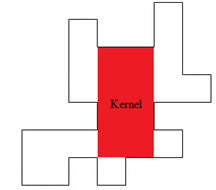 | Figure 10. The staircase kernel of P |
5.2. Example 2
This is an example of a simply connected orthogonal polygon P with no holes such that the algorithm will have an empty output.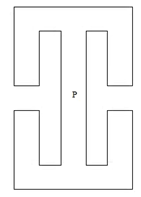 | Figure 11. An orthogonal polygon P |
Part A: Step 1 yields the Horizontal Convex Regions list, while Step 2 yields the Vertical Convex Regions list.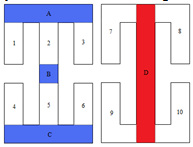 | Figure 12. Horizontal sweep and vertical sweep of P |
| Table 5. Sweep, the vertical and horizontal lists |
| | Horizontal Convex Regions | Vertical Convex Regions | | A | 7 8 | | 1 2 3 | D | | B | 9 10 | | 4 5 6 | | C |
|
|
Part A: Step 3 intersects the horizontal convex regions and the vertical convex regions to yield the updated lists containing regions that are both horizontally and vertically convex. Note that region D is partitioned into D1, D2, and D3, while regions A, and C are reduced in size.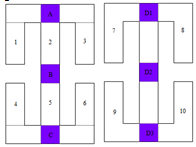 | Figure 13. Intersections of the horizontal and vertical convex regions |
| Table 6. The updated lists |
| | Horizontal Convex Regions | Vertical Convex Regions | | A | 7 8 | | 1 2 3 | D1 D2 D3 | | B | 9 10 | | 4 5 6 | | C |
|
|
Part B: Step 1 checks the staircase visibility of the questionable regions in the Horizontal Convex Regions list, and yields that region A, and C are successful regions.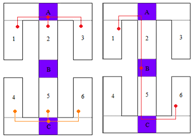 | Figure 14. Staircase visibility check of the horizontal convex regions |
| Table 7. Updated horizontal list after the visibility check |
| | Horizontal Convex Regions | | A(success) | | 1 2 3 | | B(fails) | | 4 5 6 | | C(success) |
|
|
Part B: Step 2 checks the staircase visibility of the questionable regions in the Vertical Convex Regions list, and yields that no region is successful.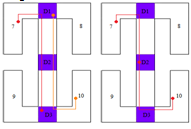 | Figure 15. Staircase visibility check of the vertical convex regions |
| Table 8. Updated vertical list after the visibility check |
| | Vertical Convex Regions | | 7 8 | | D1(fails) D2(fails) D3(fails) | | 9 10 |
|
|
Part B: Step 3 finds that regions A, and C were successful in the staircase visibility step. But since both regions do not correspond to any successful regions in the other list, the output is empty. Thus P has no staircase kernel and is thus not star-shaped via staircase paths.
5.3. Example 3
This is an example of a simply connected orthogonal polygon P with holes such that the algorithm will have a non-empty output.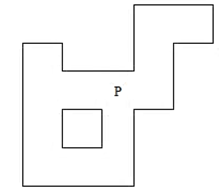 | Figure 16. An orthogonal polygon P with holes |
Part A: Step 1 yields the Horizontal Convex Regions list, while Step 2 yields the Vertical Convex Regions list.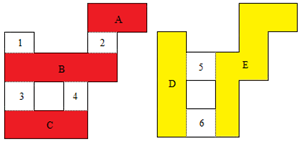 | Figure 17. Horizontal sweep and vertical sweep of P |
| Table 9. Sweep, the vertical and horizontal lists |
| | Horizontal Convex Regions | Vertical Convex Regions | | A | D | | 1 2 | 5 6 | | B | E | | 3 4 | | C |
|
|
Part A: Step 3 intersects the horizontal convex regions and the vertical convex regions to yield the updated lists containing regions that are both horizontally and vertically convex. Note that region B is partitioned into B1, and B2, region C is partitioned into C1, and C2, region D is partitioned into D1, and D2, and region E is partitioned into E1, and E2, and E3, while region A does not change.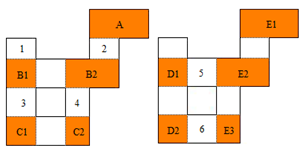 | Figure 18. Intersections of the horizontal and vertical convex regions |
| Table 10. The updated lists |
| | Horizontal Convex Regions | Vertical Convex Regions | | A | D1 D2 | | 1 2 | 5 6 | | B1 B2 | E1 E2 E3 | | 3 4 | | C1 C2 |
|
|
Part B: Step 1 checks the staircase visibility of the questionable regions in the Horizontal Convex Regions list, and yields that region B1, B2, C1, and C2 are successful regions.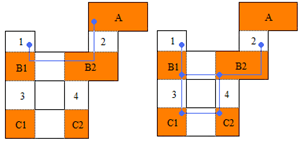 | Figure 19. Staircase visibility check of the horizontal convex regions |
| Table 11. Updated horizontal list after the visibility check |
| | Horizontal Convex Regions | | A(fails) | | 1 2 | | B1(success) B2(success) | | 3 4 | | C1(success) C2(success) |
|
|
Part B: Step 2 checks the staircase visibility of the questionable regions in the Vertical Convex Regions list, and yields that all regions are successful.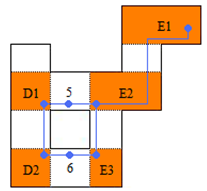 | Figure 20. Staircase visibility check of vertical convex regions |
| Table 12. Updated vertical list after the visibility check |
| | Vertical Convex Regions | | D1(success) D2(success) | | 5 6 | | E1(success) E2(success) E3(success) |
|
|
Part B: Step 3 finds that the only region that is unsuccessful in the staircase visibility step is A. So region A and region E1 which corresponds to A are not part of the output. Then the staircase kernel is determined by the regions defined by B1 and D1, B2 and E2, C1 and D2, and C2 and E3. In this case there are multiple corresponding successful regions, so the staircase kernel is disjoint, but each piece is in itself a convex orthogonal polygon. Thus P is star-shaped via staircase paths.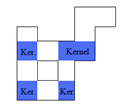 | Figure 21. The staircase kernel of P |
6. Conclusions
As we can see, given a simply connected orthogonal polygon P possibly with holes, in the plane, we can find the staircase kernel of P in O(n2) time using the plane sweep method. As shown, if P is an orthogonal polygon without holes, the staircase kernel is a single region within P. If P is an orthogonal polygon with holes, it is possible for the staircase kernel to be disjoint within P.
ACKNOWLEDGEMENTS
Dr. Vassilev’s work is supported by NSERC Discovery Grant. Stefan Pape wants to acknowledge the help of Dr. Vassilev during the work on this paper.
References
| [1] | M. Breen, Staircase kernels in orthogonal polygons. Archiv der Mathematik 59, 588-594 (1992) |
| [2] | R. Motwani, ARaghunathan, and H. Saran, Covering Orthogonal Polygons with Star Polygons; The Perfect Graph Approach. Journal of Computer System Science 40, 19-48 (1990). |
| [3] | L. Gewali, Recognizing S-Star Polygons. In Proceedings of CCCG, 183-188 (1994) |
| [4] | Mark de Berg, Marc van Kreveld, Mark Overmars, Otfried Schwarzkopf, Computational Geometry: Algorithms and Applications. Second Edition, Springer-Verlag (2000) |

 from point p to point q is referred to as an orthogonal path or orthogonal chain if its edges are parallel to the coordinate axes and alternate in direction, and thus p “sees” q. As it can be seen in Figure 2, any simply connected orthogonal polygon is convex in terms of visibility by orthogonal paths. Further refinement of the concept is the introduction of the notion of staircase paths. An orthogonal path is called a staircase path, if the turns along the path alternate between +90° and−90°. A polygon P is star-shaped via staircase paths if there is a point p in P that sees every other point of P via staircase paths.We now introduce the concept of orthogonal polygons (rectilinear polygon). A polygon P in the plane is orthogonal if its edges are parallel to the coordinate axes, thus its edges meet at right-angles, and the interior angle at each vertex is either 90° or 270°.
from point p to point q is referred to as an orthogonal path or orthogonal chain if its edges are parallel to the coordinate axes and alternate in direction, and thus p “sees” q. As it can be seen in Figure 2, any simply connected orthogonal polygon is convex in terms of visibility by orthogonal paths. Further refinement of the concept is the introduction of the notion of staircase paths. An orthogonal path is called a staircase path, if the turns along the path alternate between +90° and−90°. A polygon P is star-shaped via staircase paths if there is a point p in P that sees every other point of P via staircase paths.We now introduce the concept of orthogonal polygons (rectilinear polygon). A polygon P in the plane is orthogonal if its edges are parallel to the coordinate axes, thus its edges meet at right-angles, and the interior angle at each vertex is either 90° or 270°.

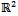 . If P is a union of maximal orthogonally convex polygons which have a common intersection that is convex. Then P is star-shaped via staircase paths.Proof: Let ker P refer to the staircase kernel of P, and P be a simply connected polygon in the plane. Let M denote the family of all maximal orthogonally convex polygons in P, and let ker P = ∩ { m : m in M}. Choose any point x ∈ ker P, and y ∈ P. Then since y ∈ P, y ∈ m in M and since ker P = ∩ {m : m in M}, there is a staircase path λ from x to y since each m in M is convex. Thus for all x ∈ ker P, and y ∈ P, x sees y via staircase paths, and thus P is star-shaped.By analysing the converse we can observe that given an orthogonal polygon P in the plane, we can decompose P into maximal orthogonally convex polygons. Then their intersection will be the staircase kernel of P. In Figure 3, given P observe that the red and the blue polygons are the maximal orthogonally convex subpolygon decomposition of P, and their intersection yields the staircase kernel shown in green.
. If P is a union of maximal orthogonally convex polygons which have a common intersection that is convex. Then P is star-shaped via staircase paths.Proof: Let ker P refer to the staircase kernel of P, and P be a simply connected polygon in the plane. Let M denote the family of all maximal orthogonally convex polygons in P, and let ker P = ∩ { m : m in M}. Choose any point x ∈ ker P, and y ∈ P. Then since y ∈ P, y ∈ m in M and since ker P = ∩ {m : m in M}, there is a staircase path λ from x to y since each m in M is convex. Thus for all x ∈ ker P, and y ∈ P, x sees y via staircase paths, and thus P is star-shaped.By analysing the converse we can observe that given an orthogonal polygon P in the plane, we can decompose P into maximal orthogonally convex polygons. Then their intersection will be the staircase kernel of P. In Figure 3, given P observe that the red and the blue polygons are the maximal orthogonally convex subpolygon decomposition of P, and their intersection yields the staircase kernel shown in green.
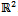 , if a region is convex, then the following region is non-convex. The converse is also true.Lemma 2: During the plane sweep of a polygon P in
, if a region is convex, then the following region is non-convex. The converse is also true.Lemma 2: During the plane sweep of a polygon P in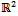 , while sweeping a non-convex region and a new edge enters the queue, if the edge is disjoint from the current regions, a new region is defined; else it is determined to be part of one of the current regions.Lemma 3: During the plane sweep of a polygon P in
, while sweeping a non-convex region and a new edge enters the queue, if the edge is disjoint from the current regions, a new region is defined; else it is determined to be part of one of the current regions.Lemma 3: During the plane sweep of a polygon P in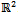 , a region becomes closed if it encounters another defined region.Lemma 4: Regions within an orthogonal polygon P that are not vertically and horizontally convex are not part of the staircase kernel of P.Lemma 5: The intersections of horizontal convex regions with vertically convex regions within a polygon are horizontally and vertically convex.Lemma 6: The staircase kernel of a polygon P is vertically and horizontally convex [1, Theorem 1].Lemma 7: If there are multiple regions within a star-shaped polygon P that “see” every point in P via staircase paths, then the staircase kernel of P is disjoint.
, a region becomes closed if it encounters another defined region.Lemma 4: Regions within an orthogonal polygon P that are not vertically and horizontally convex are not part of the staircase kernel of P.Lemma 5: The intersections of horizontal convex regions with vertically convex regions within a polygon are horizontally and vertically convex.Lemma 6: The staircase kernel of a polygon P is vertically and horizontally convex [1, Theorem 1].Lemma 7: If there are multiple regions within a star-shaped polygon P that “see” every point in P via staircase paths, then the staircase kernel of P is disjoint. Output: The staircase kernel of P
Output: The staircase kernel of P

















 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML