G. M. Moatimid , M. H. M. Moussa , Rehab M. El-Shiekh , A. A. El-Satar
Department of Mathematics, Faculty of Education, Ain Shams University, Roxy, Hiliopolis, Cairo, Egypt
Correspondence to: A. A. El-Satar , Department of Mathematics, Faculty of Education, Ain Shams University, Roxy, Hiliopolis, Cairo, Egypt.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
In this paper, we have analyzed the integrability properties of complexly coupled KdV system, and discuss the integrability properties through Painlevé (P) analysis. Further, we using Bäcklund transformation to obtain exact solutions of complexly coupled KdV system
Keywords:
Integrability, PainlevÉ Property (PP), Bäcklund Transformation and Exact Solution
1. Introduction
The study of the importance of the connection of integrability and Painlevé property (PP), in the context of ODEs, has drawn much attention in the recent literature[1-7]. In fact, the study has been well utilized, both in the original sense of Ablowitz et al.[3] and in the generalized form of Weiss et al.[5], to describe the connection of PDEs of the Painlevé type and Lax pairs, Bäcklund transformation, symmetry vector fields and recursion operators[8]. However, the technique of singular manifold expansion developed for obtaining the connection of PDEs possessing PP and Lax pairs, Bäcklund transformations, etc. in the case of integrable systems could not receive any attention for its carry over to non-integrable evolution equations. Consequently, we have, herein find the integrability properties associated with the (1 + 1) complexly coupled KdV system[9]. The system can be written in the form: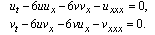 | (1.1) |
2. The Painlevé Analysis
In this part, we study the Painlevé integrability of Eq. (1.1) following the Weiss's algorithm [8] of singularity analysis. To proceed with the Painlevé singularity analysis, set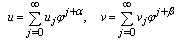 | (2.1) |
Where θ(x,t)=0, the "expansion coefficients" uj and vj are analytic functions of independent variables;(x,t)=0, describe the singular manifold, α, β are an integer to be determined. Insert expansion (2.1) in Eq. (1.1) a leading order analysis uniquely values α and β. Consequently, the said analysis yields: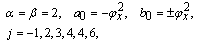 | (2.2) |
The recursion relation for uj (x,t) and vj (x,t) are found to be: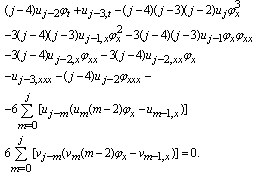 | (2.3) |
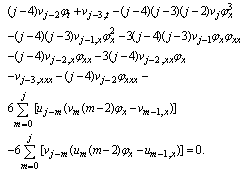 | (2.4) |
Assigning j = 0, 1, 2 in Eqs. (2.3) and (2.4), we getj=0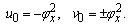 | (2.5) |
j=1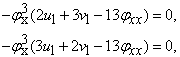 | (2.6) |
j=2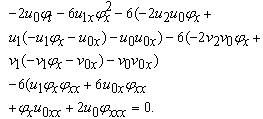 | (2.7) |
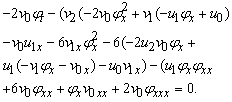 | (2.8) |
j=3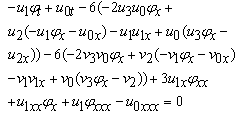 | (2.9) |
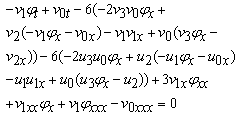 | (2.10) |
j=4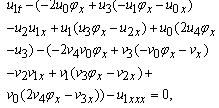 | (2.11) |
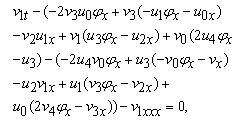 | (2.12) |
j=5 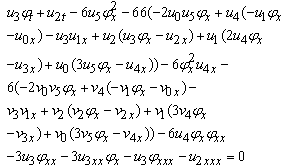 | (2.13) |
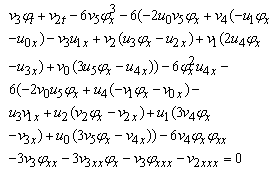 | (2.14) |
j=6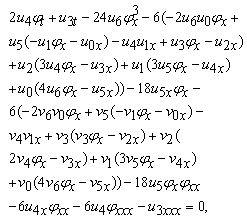 | (2.15) |
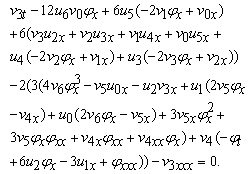 | (2.16) |
Therefore, we know for resonance Laurent series (2.1) admits the sufficient number of arbitrary functions. So it is concluded that the complexly coupled KdV system (1.1) possesses Painlevé property.
3. Bäcklund Transformation and Special Solutions
Up to know, we have determined that the coupled KdV system is integrable in the sense of having Painlevé property. To obtain the more integrable information of this equation, in the following, we give the Bäcklund transformation and some special solutions of this system. If we now apply the usual technique of determination of the "resonances" by cutting of series (2.1), we set uj=vj=0 and i≥3, then we have: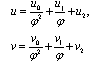 | (2.17) |
By solving Eqs. (2.6) we get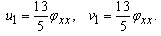 | (2.18) |
So we obtain the Bäcklund transformation of Eq. (1.1)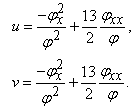 | (2.19) |
In the following, we derive the explicit special solutions for (1.1) by the Bäcklund transformation (2.19). To do this, we take two cases of φ:Case I: φ=Exp(wx+ct)+Exp(-(wx+ct)) we obtain the soliton solution of Eq. (1.1)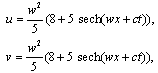 | (2.20) |
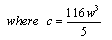 Case II: ϕ=Exp(wx+ct)-Exp(-(wx+ct)) we can write the solution of Eq. (1.1) in the form
Case II: ϕ=Exp(wx+ct)-Exp(-(wx+ct)) we can write the solution of Eq. (1.1) in the form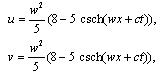 | (2.21) |
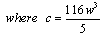
4. Conclusions
Thus, the Painlevé analysis is one of the most important methods to identify the integrability cases and the integrability properties of complexly coupled KdV system. In this paper, we applied the Painlevé analysis to complexly coupled KdV system and established their integrability properties. Also, by truncating the Laurent series at the constant level term, we have constructed the Bäcklund transformation. We obtained exact solutions of the system.
References
| [1] | J. B. Mcleod and P. J. Olver, Siam J. Math. Anal. 14, 488 (1983). |
| [2] | J. Weiss, M. Tabor, G. Carnevale, J. Math. Phys. 24 (1983) 522.526. |
| [3] | J. WEISS, J. Math. Phys. 25, 13 (1984). |
| [4] | O. P. Bhutani and M. H. M. Moussa, Int. Z Engng Sci. Vol, 33, No. 3, pp. 331-334, 1995. |
| [5] | T. Alagesan and K. Porsezian. Ch., Sol. & Fmckzfs Vol. 7, No. 8,1996. |
| [6] | T. Alagesan and K. Porsezian. Ch., Sol. & Fmckzfs Vol. 7, No. 8,1996. |
| [7] | Deng-Shan Wang, Applied Math. and Com. 216 (2010) 1349.1354. |
| [8] | W. H. Steeb and N. Euler, World Scienti.c, Singapore (1988). |
| [9] | R. Naz, . Commun Nonlinear Sci Numer Simulat 15 (2010) 1177.1182. |
| [10] | M. H. M. Moussa, Intern. Journal of Engin. Sci. 39 (2001) 1565-1575. |
| [11] | R.K. Gupta, K. Singh. Intern. Journal of Engin. Sci. 44 (2006) 241.255. |

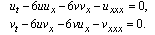
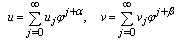
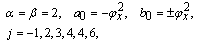
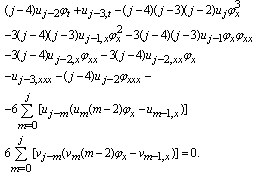
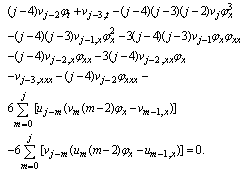
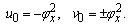
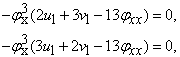
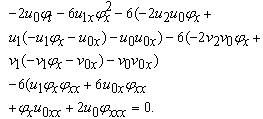
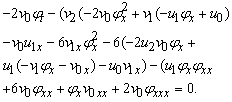
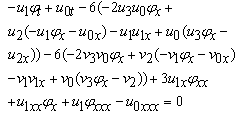
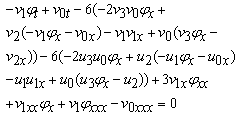
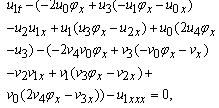
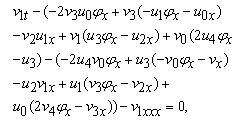
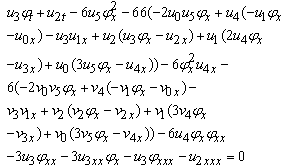
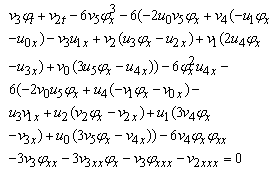
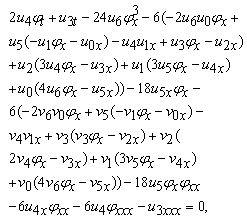
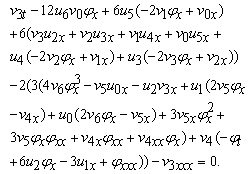
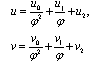
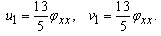
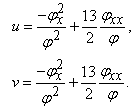
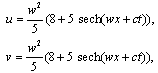
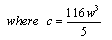 Case II: ϕ=Exp(wx+ct)-Exp(-(wx+ct)) we can write the solution of Eq. (1.1) in the form
Case II: ϕ=Exp(wx+ct)-Exp(-(wx+ct)) we can write the solution of Eq. (1.1) in the form
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML