Umar Ahmad Egbako 1, Kayode R. Adeboye 2
1Department of Mathematics and Statistics, Niger State Polytechnic, Zungeru, Nigeria
2Department of Mathematics and Statistics, Federal University of Technology, Minna, Nigeria
Correspondence to: Umar Ahmad Egbako , Department of Mathematics and Statistics, Niger State Polytechnic, Zungeru, Nigeria.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
The paper describes a one-step, six-order method for treating stiff differential equations using Pade rational functions. Dalquist’s model test equation was used to analyze its basic properties. The results show that the method is consistent and convergent. Numerical results and comparative analysis with some methods show that the method is very efficient and more accurate.
Keywords:
Stability, L-stability, Stiff, Stiffness
1. Introduction
The initial value problem given by 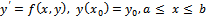 | (1) |
is considered for one-step numerical method with the order k=6. This class of problem has a lot of applications in many areas such as electrical network, chemical kinetics, control theory, mechanical, biological economic systems, etc.Definition: A system of ordinary differential equations of the form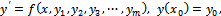 | (2) |
is said to be stiff if the eigenvalues 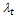 of the Jacobian matrix
of the Jacobian matrix 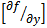 at every integration point x have negative real parts and differ greatly in magnitude, i.e. the eigenvalues
at every integration point x have negative real parts and differ greatly in magnitude, i.e. the eigenvalues 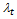 satisfy the conditions[6]. (i)
satisfy the conditions[6]. (i) 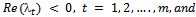 (ii)
(ii) 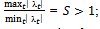 ;S is the stiffness ratioMost conventional numerical methods cannot cope with stiff problems as they lack adequate stability characteristics. For this reason a lot of researches have been carried out on stiff differential equations. Several authors like Fatunla(1976, 1980), Butcher(2000,2001,2002) as cited in[1],[2] and many others have developed A-stable methods for solving stiff initial value problems in ordinary differential equations.A one-step, fifth order method for solving this class of problem was developed[5].Liniger and Willoigbby(1970) as cited in[1] introduced the concept of exponential fitting and suggested three new A-stable methods with k=1.A sixth order multi-derivative multistep methods with step number k=2 has also been developed[1].The aim of this paper therefore is to derive a more efficient L-stable method based on Pade rational approximations.
;S is the stiffness ratioMost conventional numerical methods cannot cope with stiff problems as they lack adequate stability characteristics. For this reason a lot of researches have been carried out on stiff differential equations. Several authors like Fatunla(1976, 1980), Butcher(2000,2001,2002) as cited in[1],[2] and many others have developed A-stable methods for solving stiff initial value problems in ordinary differential equations.A one-step, fifth order method for solving this class of problem was developed[5].Liniger and Willoigbby(1970) as cited in[1] introduced the concept of exponential fitting and suggested three new A-stable methods with k=1.A sixth order multi-derivative multistep methods with step number k=2 has also been developed[1].The aim of this paper therefore is to derive a more efficient L-stable method based on Pade rational approximations.
2. Derivation of the Method
We consider Pade rational approximant of the form: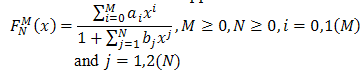 | (3) |
where 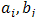 are real coefficients[7] and[8].We define a finite difference numerical integrator of maximal order K=M+N for approximating initial value problem
are real coefficients[7] and[8].We define a finite difference numerical integrator of maximal order K=M+N for approximating initial value problem  by
by 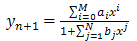 | (4) |
with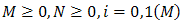 and j=1,2(N)The parameters
and j=1,2(N)The parameters 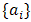 and
and 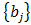 are constant coefficients to be determined.To develop a one-step, six-order method we set M=3,N=3 in equation (4):
are constant coefficients to be determined.To develop a one-step, six-order method we set M=3,N=3 in equation (4):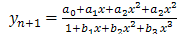 | (5) |
If we adopt Taylor series of 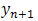 and ignore terms of order higher than 6 in equation (5), we obtain:
and ignore terms of order higher than 6 in equation (5), we obtain: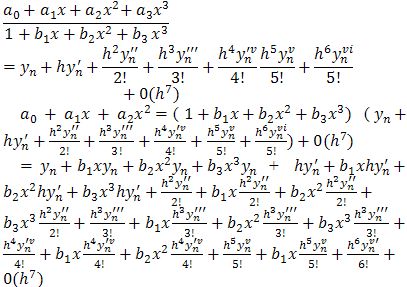 Taking, x=h, and equating the coefficients as far as h6, we have
Taking, x=h, and equating the coefficients as far as h6, we have 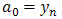 | (6) |
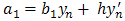 | (7) |
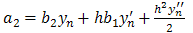 | (8) |
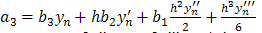 | (9) |
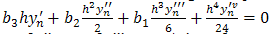 | (10) |
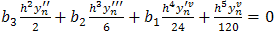 | (11) |
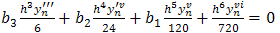 | (12) |
Solving for b1, b2 and b3 in (10),(11),(12), we have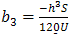 | (13) |
where 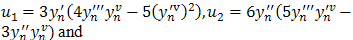
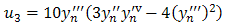 | (14) |
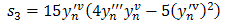 | (15) |
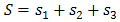
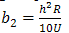 | (16) |
where 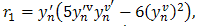
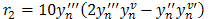
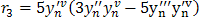 | (17) |
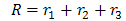
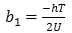 | (18) |
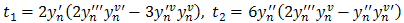 and
and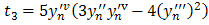 | (19) |
T=t1+t2+t3Substituting b1 in (7) and simplify, we have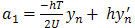
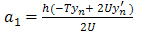 | (20) |
Substituting b1 and b2in (8) and simplify, we have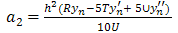 | (21) |
Also substituting b1, b2 and b3 in (9) and simplify, we have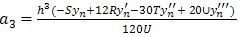 | (22) |
We put 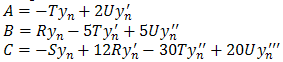 Substituting the values of a0, a1, a2, b1, b2and b3 in (5), we obtain
Substituting the values of a0, a1, a2, b1, b2and b3 in (5), we obtain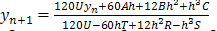 | (23) |
Where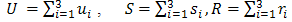 , and
, and 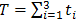 and the
and the 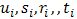 are as given in equations (14), (15), (17) and (19) respectively and equation (23) gives the desired method.
are as given in equations (14), (15), (17) and (19) respectively and equation (23) gives the desired method.
3. Convergence of the Method
We establish the convergence of the method by showing that the method is consistent and stable.Theorem 1: The one-step, sixth-order method (23) above is consistent and convergent[4].Proof A one-step numerical method of the form:, is convergent if and only if it is consistentIf we subtract yn from both sides of (23), we have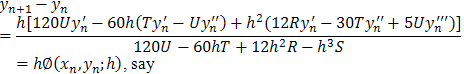 Hence
Hence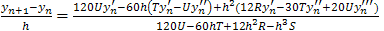 | (24) |
Then 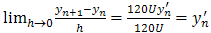 | (25) |
This implies that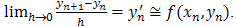 .This implies that the method is consistent with the initial value problem
.This implies that the method is consistent with the initial value problem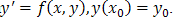 . Hence the method is convergent.Theorem 2: The method (23) is L-Stable[4].ProofIf we apply to the method (23), the well-known Dahlquist stability test equation[3].
. Hence the method is convergent.Theorem 2: The method (23) is L-Stable[4].ProofIf we apply to the method (23), the well-known Dahlquist stability test equation[3].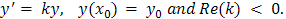 | (26) |
We have,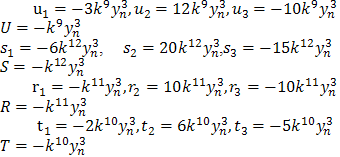 Then
Then 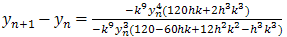 | (27) |
Hence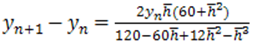 | (28) |
where 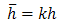 Setting
Setting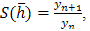 we have
we have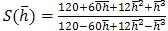 | (29) |
is the stability function of the method (23)Obviously from equation (28) as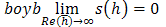 | (30) |
Therefore the method is L-Stable.
4. Implementation of the Method
We demonstrated the efficiency of our method on stiff ordinary differential equation by considering one -dimensional differential equation: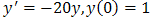 We applied Explicit Euler method:
We applied Explicit Euler method: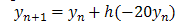 The results for a number of h values (step length) are shown in figure 1. A very small step size is required for a reasonable solution as we can see in the figure below.
The results for a number of h values (step length) are shown in figure 1. A very small step size is required for a reasonable solution as we can see in the figure below.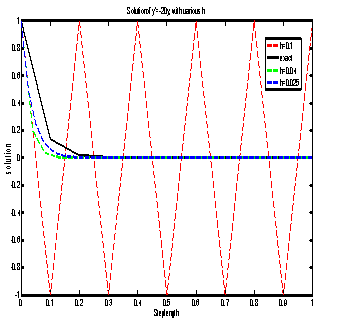 | Figure 1. Explicit Euler Method with various step sizes |
However, if we use implicit Euler method 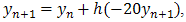 The solution is reasonable even for the relatively large value of h=0.1. This result can be seen in figure 2. We therefore compared the performance of our method with implicit Euler method. As we can see in figure 3 our method performs very efficiently as the solution coincides with the exact solution. Its performance is better than that of implicit Euler method which is known to cope with stiff ordinary differential equations.Problem 1:
The solution is reasonable even for the relatively large value of h=0.1. This result can be seen in figure 2. We therefore compared the performance of our method with implicit Euler method. As we can see in figure 3 our method performs very efficiently as the solution coincides with the exact solution. Its performance is better than that of implicit Euler method which is known to cope with stiff ordinary differential equations.Problem 1: 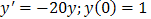
Table 1. Shows The Performance Of Our Methods Against The Exact Solution, Compared With Euler Methods
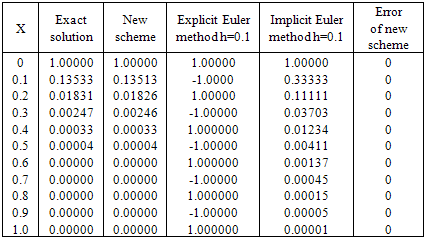 |
| |
|
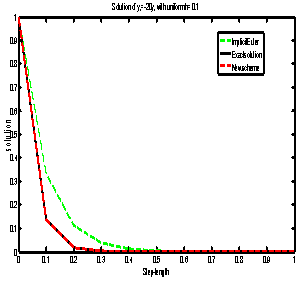 | Figure 2. Comparison of the New Method with Implicit Euler Method on Stiff Differential Equation |
Problem 2: Second Order Differential EquationWe illustrate the accuracy and efficiency of our new method on the solution of second order differential equation: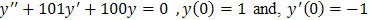 By setting
By setting 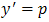
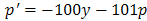 we have a 2x2 stiff system with the initial conditions y(0)=1 and p(0)= -1The eigenvalues of the Jacobian matrix of the equation are λ1=−1 and λ2=−2 This problem is solved using our new method with h=2 and the results are given in table 2 below.
we have a 2x2 stiff system with the initial conditions y(0)=1 and p(0)= -1The eigenvalues of the Jacobian matrix of the equation are λ1=−1 and λ2=−2 This problem is solved using our new method with h=2 and the results are given in table 2 below.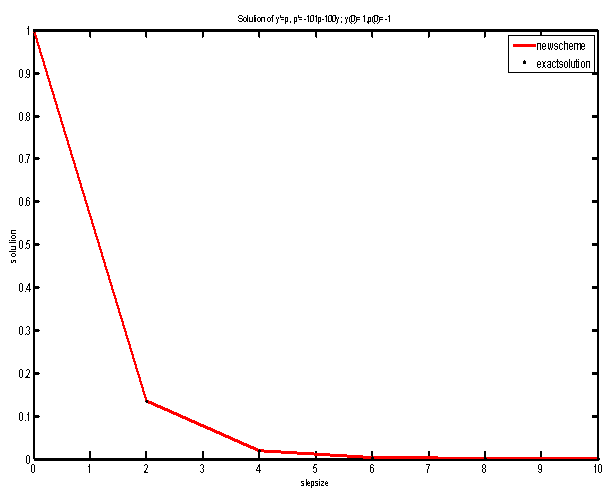 | Figure 3. Comparison of the New Method with Theoretical Solution on Stiff Differential Equation |
| Table 2. Shows the performance of our method compared with exact solutio |
| | X | Exact solution | New scheme | Error | | 0246810 | 1.000000000000000 0.135335283236613 0.018315638888734 0.002478752176666 0.000335462627903 0.000045399929762 | 1.000000000000000 0.135135135135135 0.018261504747991 0.002467770911891 0.000333482555661 0.000045065210224 | 0 2.0e-06 5.1e-06 1.0e-06 1.9e-06 3.3e-07 |
|
|
5. Conclusions
The theoretical analysis showed that our new method is a good numerical method for the treatment initial value problems and also efficient in solving stiff differential equations. We observed that our method needs not use a small step size as it may be required by other methods before a good accuracy is achieved.The method will therefore be useful in the solution of problems arising from electrical networks, economy affected by inflations and chemical reactions.
ACKNOWLEDGEMENTS
Were we to acknowledge the whole extent of our indebtedness to others, we should transfer to this point the bibliography which appears as reference. But passing over those to whom we are indebted through their published work, we feel it our duty to mention two names in particular. To Prof. S. O. Fatunla and Prof. Henri Padé we owe our introduction to the subject.
References
| [1] | Abhulemen, C. E., and Otunta, F. O.2006, A sixth order multi-derivative multistep methods for stiff systems. International Journal of Numerical Mathematics, (1), 248-268. |
| [2] | Ademiluyi, R. A., 2004, Effects of inaccurate derivative approximation on stiff odes solvers. Newton-Raphson method as a case study, Journal of mathematical Association of Nigeria, 31(2A),130-135 |
| [3] | Dahlquist, G., 1963, A special stability problem for linear multi-step methods, BIJ, pp. 27-43. |
| [4] | Fatunla, S. O., “Numerical methods for initial value problems in ordinary differential equations”, Academic Press, Boston USA, 1988 |
| [5] | Fatunla, S. O., and Aashipelokhai, U.S.U., 1994, A fifth order l-stable numerical integrator, Scientific Computing (Fatunla S. O. ed), pp. 68-86. |
| [6] | Jain, M. K., Iyengar, S. R.K., and Jain, R.K., 2007, “Numerical methods for scientific and engineering computation”, New Age International Publishers, New Dehli, India. |
| [7] | Wikipedia(2007), Stiff equations,[Online]. Available:file:///C:/Documents%20and%20Settings/All%20Users/Documents/Sti. |
| [8] | Wikipedia (2009), Pade approximant,[Online]. Available:file://///Thompson-pc/public/PadeApproximationMod_Ink_2.html |
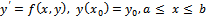
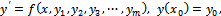
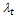 of the Jacobian matrix
of the Jacobian matrix 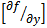 at every integration point x have negative real parts and differ greatly in magnitude, i.e. the eigenvalues
at every integration point x have negative real parts and differ greatly in magnitude, i.e. the eigenvalues 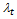 satisfy the conditions[6]. (i)
satisfy the conditions[6]. (i) 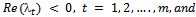 (ii)
(ii) 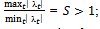 ;S is the stiffness ratioMost conventional numerical methods cannot cope with stiff problems as they lack adequate stability characteristics. For this reason a lot of researches have been carried out on stiff differential equations. Several authors like Fatunla(1976, 1980), Butcher(2000,2001,2002) as cited in[1],[2] and many others have developed A-stable methods for solving stiff initial value problems in ordinary differential equations.A one-step, fifth order method for solving this class of problem was developed[5].Liniger and Willoigbby(1970) as cited in[1] introduced the concept of exponential fitting and suggested three new A-stable methods with k=1.A sixth order multi-derivative multistep methods with step number k=2 has also been developed[1].The aim of this paper therefore is to derive a more efficient L-stable method based on Pade rational approximations.
;S is the stiffness ratioMost conventional numerical methods cannot cope with stiff problems as they lack adequate stability characteristics. For this reason a lot of researches have been carried out on stiff differential equations. Several authors like Fatunla(1976, 1980), Butcher(2000,2001,2002) as cited in[1],[2] and many others have developed A-stable methods for solving stiff initial value problems in ordinary differential equations.A one-step, fifth order method for solving this class of problem was developed[5].Liniger and Willoigbby(1970) as cited in[1] introduced the concept of exponential fitting and suggested three new A-stable methods with k=1.A sixth order multi-derivative multistep methods with step number k=2 has also been developed[1].The aim of this paper therefore is to derive a more efficient L-stable method based on Pade rational approximations.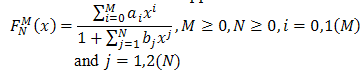
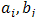 are real coefficients[7] and[8].We define a finite difference numerical integrator of maximal order K=M+N for approximating initial value problem
are real coefficients[7] and[8].We define a finite difference numerical integrator of maximal order K=M+N for approximating initial value problem  by
by 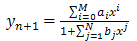
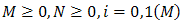 and j=1,2(N)The parameters
and j=1,2(N)The parameters 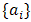 and
and 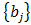 are constant coefficients to be determined.To develop a one-step, six-order method we set M=3,N=3 in equation (4):
are constant coefficients to be determined.To develop a one-step, six-order method we set M=3,N=3 in equation (4):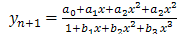
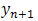 and ignore terms of order higher than 6 in equation (5), we obtain:
and ignore terms of order higher than 6 in equation (5), we obtain: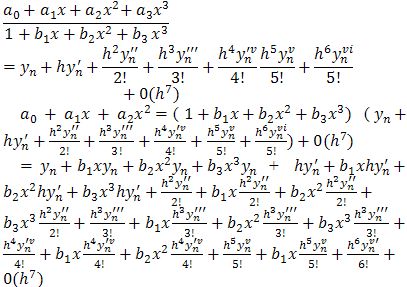 Taking, x=h, and equating the coefficients as far as h6, we have
Taking, x=h, and equating the coefficients as far as h6, we have 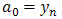
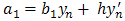
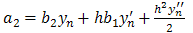
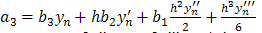
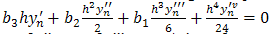
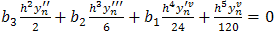
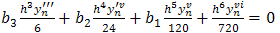
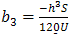
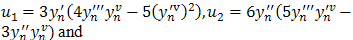
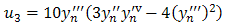
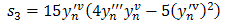
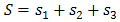
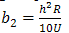
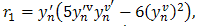
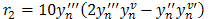
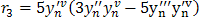
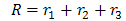
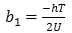
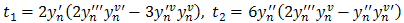 and
and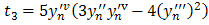
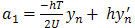
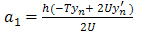
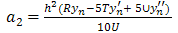
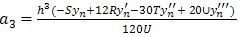
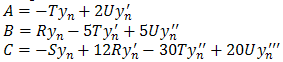 Substituting the values of a0, a1, a2, b1, b2and b3 in (5), we obtain
Substituting the values of a0, a1, a2, b1, b2and b3 in (5), we obtain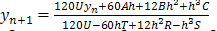
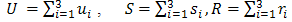 , and
, and 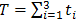 and the
and the 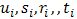 are as given in equations (14), (15), (17) and (19) respectively and equation (23) gives the desired method.
are as given in equations (14), (15), (17) and (19) respectively and equation (23) gives the desired method.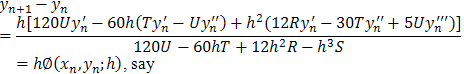 Hence
Hence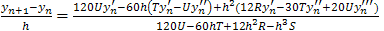
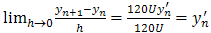
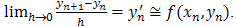 .This implies that the method is consistent with the initial value problem
.This implies that the method is consistent with the initial value problem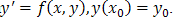 . Hence the method is convergent.Theorem 2: The method (23) is L-Stable[4].ProofIf we apply to the method (23), the well-known Dahlquist stability test equation[3].
. Hence the method is convergent.Theorem 2: The method (23) is L-Stable[4].ProofIf we apply to the method (23), the well-known Dahlquist stability test equation[3].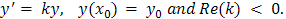
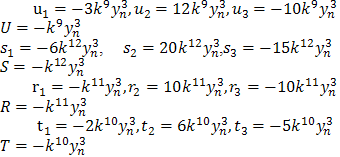 Then
Then 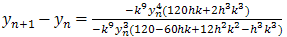
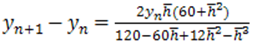
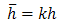 Setting
Setting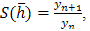 we have
we have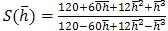
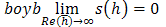
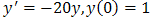 We applied Explicit Euler method:
We applied Explicit Euler method: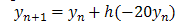 The results for a number of h values (step length) are shown in figure 1. A very small step size is required for a reasonable solution as we can see in the figure below.
The results for a number of h values (step length) are shown in figure 1. A very small step size is required for a reasonable solution as we can see in the figure below.
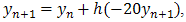 The solution is reasonable even for the relatively large value of h=0.1. This result can be seen in figure 2. We therefore compared the performance of our method with implicit Euler method. As we can see in figure 3 our method performs very efficiently as the solution coincides with the exact solution. Its performance is better than that of implicit Euler method which is known to cope with stiff ordinary differential equations.Problem 1:
The solution is reasonable even for the relatively large value of h=0.1. This result can be seen in figure 2. We therefore compared the performance of our method with implicit Euler method. As we can see in figure 3 our method performs very efficiently as the solution coincides with the exact solution. Its performance is better than that of implicit Euler method which is known to cope with stiff ordinary differential equations.Problem 1: 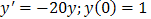

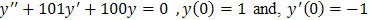 By setting
By setting 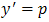
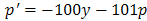 we have a 2x2 stiff system with the initial conditions y(0)=1 and p(0)= -1The eigenvalues of the Jacobian matrix of the equation are λ1=−1 and λ2=−2 This problem is solved using our new method with h=2 and the results are given in table 2 below.
we have a 2x2 stiff system with the initial conditions y(0)=1 and p(0)= -1The eigenvalues of the Jacobian matrix of the equation are λ1=−1 and λ2=−2 This problem is solved using our new method with h=2 and the results are given in table 2 below.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML