-
Paper Information
- Next Paper
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Computational and Applied Mathematics
p-ISSN: 2165-8935 e-ISSN: 2165-8943
2012; 2(1): 37-40
doi: 10.5923/j.ajcam.20120201.07
Application of He’s Variational Iteration Method for Solving Seventh-Order Differential Equations
1Department of Civil Engineering, Shomal University, Amol, Iran
2Department of Architectural Engineering, Shomal University, Amol, Iran
Correspondence to: A. Nikkar , Department of Civil Engineering, Shomal University, Amol, Iran.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
In this paper, we extend variational iteration method (VIM) for deriving approximate analytical solution to seventh-order differential equations with specified initial conditions, also in this paper we applied a modified method to identification of Lagrange multiplier .By providing some examples, we illustrate the capability and reliability of the method.
Keywords: Variational Iteration Method (VIM); Seventh-Order Equations; Analytical Solutions
Cite this paper: A. Nikkar , M. Mighani , "Application of He’s Variational Iteration Method for Solving Seventh-Order Differential Equations", American Journal of Computational and Applied Mathematics , Vol. 2 No. 1, 2012, pp. 37-40. doi: 10.5923/j.ajcam.20120201.07.
Article Outline
1. Introduction
- Recently, many different methods have been introduced to solve linear and nonlinear problems, such as the homotopy analysis method[1], the variational iteration method (VIM)[2-5], Energy Balance Method[6], the Adomian’s decomposition method (ADM)[7,8], and homotopy perturbation method[9–12].Ji-Huan. He proposed a variational iteration method (VIM) based on the use of restricted variations and correction functional which has found a wide application for the solution of nonlinear ordinary and partial differential equations[13-15]. VIM has successfully been applied to many situations. For example, Batiha et al.[16] applied VIM to solve heat- and wave-like equations with singular behaviors. Furthermore, Batiha et al.[17] have expanded VIM in the form of Multistage VIM to solve a class of nonlinear system of ODEs, Wazwaz[18] applied VIM to solve linear and nonlinear Schrodinger equations. Shou et al.[19] solved heat-like and wave-like equations with variable coefficients by VIM, Sweilam[20] used VIM to solve multi-order FDEs. The VIM is capable for solving a large class of linear or nonlinear differential equations without the tangible restriction of sensitivity to the degree of the nonlinear term and also it reduces the size of calculations. In this paper, we implement the VIM for finding the approximate analytical solutions of nonlinear seventh-order equations with specified initial conditions. In the present paper we employ VIM method for solving following equation:
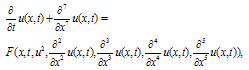 | (1) |
2. Analysis of the Variational Iteration Method (VIM)
- To illustrate the basic concept of the technique, we consider the following general differential equation4.4mm between columns.
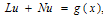 | (2) |
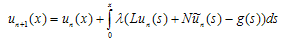 | (3) |
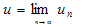 | (4) |
3. Application of the Variational Iteration Method (VIM)
- In this section, we will apply the variational iteration method (VIM) to solve following equations:
3.1. Example 1
- Consider the following differential equations of the seventh order:
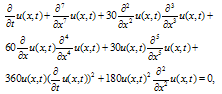 | (5) |
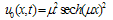 | (6) |
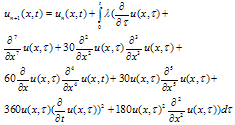 | (7) |
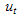 | (8) |
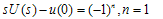 | (9) |
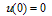 | (10) |
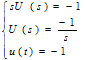 | (11) |
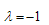 | (12) |
 | (13) |
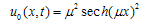 | (14) |
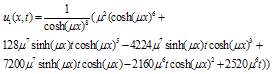 | (15) |
 | (16) |
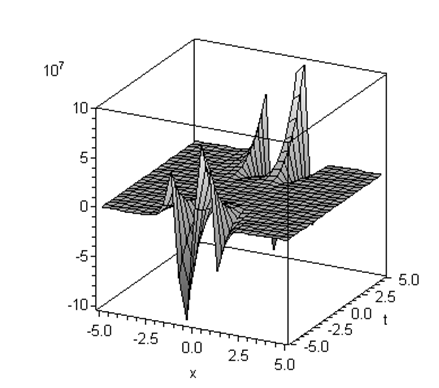 | Figure 1. The surface generated from u(x, t) of variational iteration method (VIM) for seventh-order equation when µ=0.1 |
3.2. Example 2
- Next, we consider the following equation:
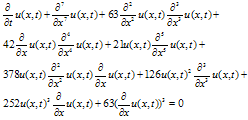 | (17) |
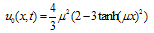 | (18) |
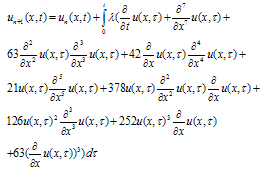 | (19) |
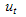 | (20) |
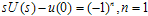 | (21) |
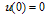 | (22) |
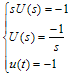 | (23) |
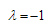 | (24) |
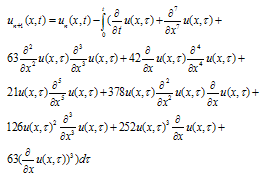 | (25) |
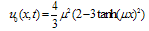 | (26) |
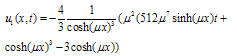 | (27) |
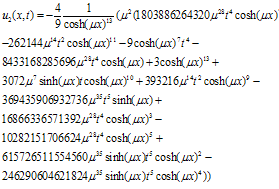 | (28) |
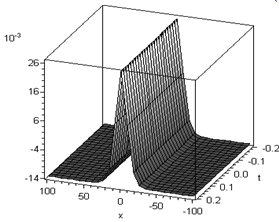 | Figure 2. The surface generated from u(x, t) of variational iteration method (VIM) for seventh-order equation when µ=0.1 |
| |||||||||||||||||||||||||||||||||||||||||||||||||||
4. Conclusions
- In the present work, illustrative examples have showed that the method provides a sequence of functions which converge to the exact solution of the aforementioned systems. The results variational iteration method (VIM) are of high concentration and the method is very effective and succinct.
ACKNOWLEDGEMENTS
- The Authors would like to express their thanks to Dr. M. Saravi for his useful comments and suggestions for improvement of this paper
References
| [1] | S.J. Liao, An approximate solution technique not depending on small parameters: a special; example, International. J. Nonlinear Mech. 303 (1995) 371–380 |
| [2] | M.A. Abdou, A.A. Soliman, Variational iteration method for solving Burger’s and coupled Burger’s equations, J. Comput. Appl. Math. 181 (2)(2005) 245–251 |
| [3] | J.H. He, Approximate analytical solution for seepage flow with fractional derivatives in porous media, Comput. Methods Appl. Mech. Eng. 167(1998) 57–68 |
| [4] | J.H. He, Approximate solution for nonlinear differential equations with convolution product nonlinearities, Comput. Methods Appl. Mech. Eng.167 (1998) 69–73 |
| [5] | J.H. He, X.H. Wu, Construction of solitary solution and compacton-like solution by variational iteration method, Chaos, Solitons Fractals 29(1) (2006) 108–113 |
| [6] | A. Nikkar, S. Esmaeilzade Toloui, K. Rashedi and H. R. Khalaj Hedayati, Application of energy balance method for a conservative X1/3 force nonlinear oscillator and the Doffing equations. Vol. 5, No. 1, 2011, 57-66 |
| [7] | [G. Adomian, Solving Frontier Problems of Physics: The Decomposition Method, Kluwer Academic, Boston, 1994 |
| [8] | A.M. Wazwaz, Partial Differential Equations: Methods and Applications, Balkema, Rottesdam, 2002 |
| [9] | D.D. Ganji, A. Rajabi, Assessment of homotopy-perturbation and perturbation methods in heat radiation equations, International. Commun. Heat Mass Transfer 33 (3) (2006) 391–400 |
| [10] | J.H. He, Homotopy perturbation technique, Comput. Methods Appl. Mech. Eng. 178 (1999) 257–262 |
| [11] | J.H. He, A coupling method of a homotopy technique and a perturbation technique for non-linear problems, International. J. Nonlinear Mech. 35(2000) 37–43 |
| [12] | J.H. He, Homotopy perturbation method for bifurcation of nonlinear problems, Int. J. Nonlinear Sci. Numer. Simul. 6 (2) (2005) 207–208 |
| [13] | He JH. Variational iteration method for autonomous ordinary differential systems. Applied Mathematics and Computation, 2000; 114: 115-123 |
| [14] | He JH. Approximate analytical solution for seepage flow with fractional derivatives in porous media. Comput Meth Appl Mech Eng 1998; 167: 57–68 |
| [15] | He JH. Approximate solution of nonlinear differential equations with convolution product nonlinearities. Comput Meth Appl Mech Eng 1998; 167: 69–73 |
| [16] | B. Batiha, M.S.M. Noorani, I. Hashim, Application of variational iteration method to heat and wave-like equations. Phys. Lett. A, doi:10.1016/j.physleta.2007.04.069 |
| [17] | B. Batiha, M.S.M. Noorani, I. Hashim, E.S. Ismail, The multistage variational iteration method for class of nonlinear system of ODEs, Phys. Scr. 76 (2007) 388–392 |
| [18] | A.M. Wazwaz, A study on linear and nonlinear Schrodinger equations by the variational iteration method, Chaos, Solitons and Fractals doi:10.1016/j.chaos.2006.10.009 |
| [19] | D.H. Shou, J.H. He, Beyond Adomian methods: The variational iteration method for solving heat-like and wave-like equations with variable coefficients, Phys. Lett. A 73 (1) (2007) 1–5 |
| [20] | N.H. Sweilam, et al. Numerical studies for a multi-order fractional differential equation, Phys. Lett. A., doi: 10. 1016/j.physleta.2007.06.016 |
| [21] | He, J. H. (1999). Variational iteration method- a kind of non-linear analytical technique: some examples, Int. J. Nonlin. Mech., 34, pp. 699-708 |
| [22] | He, J. H. (2000). Variational iteration method for autonomous ordinary differential systems, Appl. Math. Comput. 114, pp. 115-123 |
| [23] | He, J. H. (2006). Some asymptotic methods for strongly nonlinear equation, Int. J. Nod. Phy. 20(20)10, pp. 1144-1199 |
| [24] | He, J. H. and X. H. Wu (2006). Construction of solitary solutions and compacton-like solution by variational iteration method, Chos. Soltn. Frcts. 29(1), pp. 108-113 |
| [25] | Inokuti, M., H. Sekine and T. Mura (1978). General use of the Lagrange multiplier in nonlinear mathematical physics, in: S. Nemat-Nasser (Ed.), Variational Method in the Mechanics of Solids. Oxford: Pergamon Press, pp. 156-162 |
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML