Anupam Khanna1, Ashish Kumar Sharma2
1Dept. of Mathematics, MMEC, MMU (Mullana), Ambala, India
2Research Scholar, Dept. of Mathematics, MMEC, MMU (Mullana), Ambala, India
Correspondence to: Anupam Khanna, Dept. of Mathematics, MMEC, MMU (Mullana), Ambala, India.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
Visco- Elastic Plates are being increasingly used in the aeronautical and aerospace industry as well as in other fields of modern technology. Plates with variable thickness are of great importance in a wide variety of engineering applications i.e. nuclear reactor, aeronautical field, naval structure, submarine, earth-quake resistors etc. The analysis is presented here is to study the two dimensional thermal effect on vibration of visco-elastic square plate of variable thickness. Temperature & thickness both vary linearly in one direction and parabolically in another direction. A frequency equation is derived by using Rayleigh-Ritz technique with a two-term deflection function. Both the modes of the frequency are calculated by the latest computational technique, MATLAB, for the various values of taper parameters and temperature gradient.
Keywords:
Visco-Elastic, Square Plate, Vibration, Thermal Gradient, Taper Constant
Cite this paper: Anupam Khanna, Ashish Kumar Sharma, Effect of Thermal Gradient on Vibration of Visco-Elastic Plate with Thickness Variation, American Journal of Computational and Applied Mathematics , Vol. 2 No. 1, 2012, pp. 34-36. doi: 10.5923/j.ajcam.20120201.06.
1. Introduction
Since new materials and alloys are in great use in the construction of technically designed structures therefore the application of visco-elasticity is the need of the hour. Tapered plates are generally used to model the structures. Plates with thickness variability are of great importance in a wide variety of engineering applications.With the advancement of technology, the requirement to know the effect of temperature on visco-elastic plates of variable thickness has become vital due to their applications in various engineering branches such as nuclear power plants, engineering, industries etc. Further in mechanical system where certain parts of machine have to operate under elevated temperature, its effect is far from negligible and obviously cause non-homogeneity in the plate material i.e. elastic constants (young modulus etc.) of the materials becomes functions of space variables.In an up-date survey of literature, authors have come across various models to account for non-homogeneity of plate materials proposed by researchers dealing with vibration but none of them consider non-homogeneity with thermal effect on visco-elastic plates. It also indicates that sufficient work on one dimensional temperature variation has been done but negligible work has been done in the field of two dimensional temperature variation. Recently, A.K. Gupta and Anupam Khanna[1], studied the Thermal Effect on Vibrations of Parallelogram Plate of Linearly Varying Thickness. A.K. Gupta and Anupam Khanna[2], studied the Vibration of clamped visco-elastic rectangular plate with parabolic thickness variations. A.K. Gupta and Anupam Khanna[3], has been studied on Free vibration of clamped visco-elastic rectangular plate having bi-direction exponentially thickness variations. A.K. Gupta and A. Khanna[4], also studied the, Vibration of Visco- elastic rectangular plate with linearly thickness variations in both directions. Anupam Khanna, Ashish Kumar Sharma[5], studied the Study of free Vibration of Visco-Elastic Square Plate of Variable Thickness with Thermal Effect. Anupam Khanna, Ashish Kumar Sharma[6], has been studied on Vibration Analysis of Visco-Elastic Square Plate of Variable Thickness with Thermal Gradient. We assume that non homogeneity occurs in Modulus of Elasticity. For various numerical values of thermal gradient and taper constants; frequency for the first two modes of vibration are calculated with the help of latest software. All results are shown in Graphs.
2. Equation of Motion and Analysis
The governing differential equation of transverse motion of a visco-elastic plate of variable thickness in Cartesian co-ordinates, as :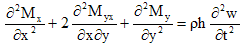 | (2.1) |
The expression for Mx, My, Myx are given by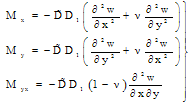 | (2.2) |
On substitution the values Mx, My and Myx from equation (2.2) in (2.1) and taking w, as a product of two functions, equal to w(x, y, t) = W(x, y) T (t), equation (2.1) becomes: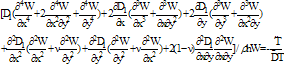 | (2.3) |
Here dot denote differentiation with respect to t. taking both sides of equation (2.3) are equal to a constant p2, we have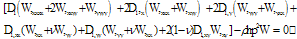 | (2.4) |
which is a differential equation of transverse motion for non-homogeneous plate of variable thickness. Here, D1 is the flexural rigidity of plate i.e. 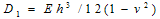 | (2.5) |
and corresponding two-term deflection function is taken as[4]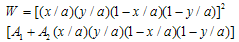 | (2.6) |
Assuming that the square plate of engineering material has a steady two dimensional i.e. linear in one direction and parabolic in another direction as shown below: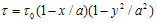 | (2.7) |
where, 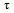 denotes the temperature excess above the reference temperature and
denotes the temperature excess above the reference temperature and 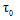 denotes the temperature at any point on the boundary of plate and “a” is the length of a side of square plate.The temperature dependence of the modulus of elasticity for most of engineering materials can be expressed in this
denotes the temperature at any point on the boundary of plate and “a” is the length of a side of square plate.The temperature dependence of the modulus of elasticity for most of engineering materials can be expressed in this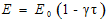 | (2.8) |
where, E0 is the value of the Young's modulus at reference temperature i.e. 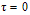 and
and 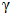 is the slope of the variation of E with. The modulus variation (2.8) become
is the slope of the variation of E with. The modulus variation (2.8) become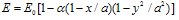 | (2.9) |
where, 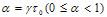 thermal gradient.It is assumed that thickness also varies in two directions i.e. linear in one direction and parabolic in another direction as shown below:
thermal gradient.It is assumed that thickness also varies in two directions i.e. linear in one direction and parabolic in another direction as shown below: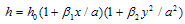 | (2.10) |
where, β1 & β2 are taper parameters in x- & y- directions respectively and h=h0 at x=y=0.Put the value of E & h from equation (2.9) & (2.10) in the equation (2.5), one obtain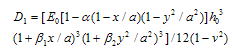 | (2.11) |
Rayleigh-Ritz technique is applied to solve the frequency equation. In this method, one requires maximum strain energy must be equal to the maximum kinetic energy. So it is necessary for the problem under consideration that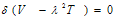 | (2.12) |
for arbitrary variations of W satisfying relevant geometrical boundary conditions. Since the plate is assumed as clamped at all the four edges, so the boundary conditions are 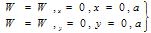 | (2.13) |
where,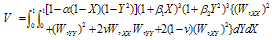 | (2.14) |
and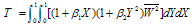 | (2.15) |
Here, 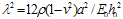 is a frequency parameter.Equation consists two unknown constants i.e. A1 & A2 arising due to the substitution of W. These two constants are to be determined as follows
is a frequency parameter.Equation consists two unknown constants i.e. A1 & A2 arising due to the substitution of W. These two constants are to be determined as follows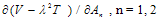 | (2.16) |
On simplifying (2.16), one gets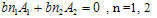 | (2.17) |
For a non-trivial solution, the determinant of the coefficient of equation (2.17) must be zero. So one gets, the frequency equation as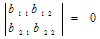 | (2.18) |
With the help of equation (2.18), one can obtains two modes of vibration of frequency i.e. λ1 (Mode1) & λ2 (Mode2).
3. Result and Discussion
All calculations are carried out with the help of latest Matrix Laboratory computer software. Computation has been done for frequency of visco-elastic square plate for different values of taper constants β1 and β2, thermal gradient α, at different points for first two modes of vibrations. 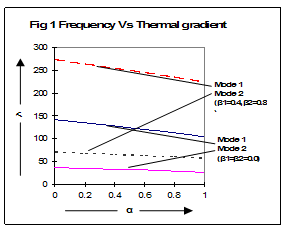 | Figure 1. Frequency vs. Thermal Gradient |
Fig 1:- It is clearly seen that value of frequency decreases as thermal gradient increases from 0.0 to 1.0 for β1=β2=0.0 and β1=0.4, β2=0.8 for both modes of vibrations. Also, note that frequency increases fast as taper parameters (β1&β2) increase from 0.0 to 0.4 and 0.8 respectively.Fig 2:- Value of frequency increases with the increment in taper parameter β1 for following cases i) α= 0.4, β2=0.2 ii) α= 0.2, β2=0.4Interesting to note that frequency increases with the increment in β1 from 0.0 to 1.0. Also, value in case (ii) is more than in case (i).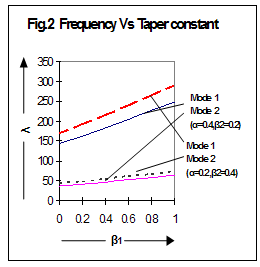 | Figure 2. Frequency vs. Taper Constant |
5. Conclusions
Results of present paper are compared with paper[6]. It is interesting to note that value of frequency has greater value in this paper as compared to[6]. So, main aim for our research is to develop a theoretical mathematical model for scientists and design engineers so that they can make a use of it with a practical approach, for the welfare of the human beings as well as for the advancement of technology.
ACKNOWLEDGEMENTS
It is with a feeling of great pleasure that we would like to express my most sincere heartfelt gratitude to Chancellor of M.M University, Haryana (INDIA), Sh. Tarsam Garg and Head of the Mathematics Dept. Prof. Deepak Gupta for providing us the necessary facilities in the department.
References
| [1] | A.K. Gupta and Anupam Khanna, Thermal Effect On Vibrations Of Parallelogram Plate Of Linearly Varying Thickness, Advanced Studies Of Theoretical Physics, 2010 , (Vol.4, No.17, pp: 817-826) |
| [2] | A.K.Gupta and Anupam Khanna, Vibration of clamped visco-elastic rectangular plate with parabolic thickness variations, Journal shock and vibration, 2008, Vol.15 (6), 713-723 |
| [3] | A.K. Gupta and Anupam Khanna, Free vibration of clamped visco-elastic rectangular plate having bi-direction exponentially thickness variations, Journal of Theoretical and Applied Mechanics, 2009, Vol. 47 (2), pp. 457-471 |
| [4] | A.K.Gupta and A. Khanna, Vibration of visco-elastic rectangular plate with linearly thickness variations in both directions, J. Sound and Vibration, 2007, Vol.301, 450-457 |
| [5] | A. Khanna, Ashish Kumar Sharma, Study of free Vibration of Visco-Elastic Square Plate of Variable Thickness with Thermal Effect, Innovative System Design and Engineering, 2011, U.S.A. Vol.2. No. 4 |
| [6] | A. Khanna, Ashish Kumar Sharma , Vibration Analysis of Visco-Elastic Square Plate of Variable Thickness with Thermal Gradient, International Journal of Engineering and Applied Sciences, Turkey, 2011, Vol. 3 - Issue 4, pp. 1-6 |

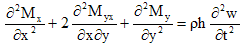
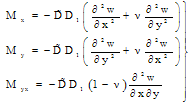
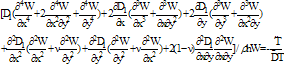
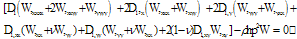
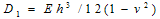
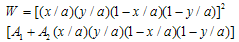
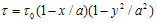
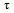 denotes the temperature excess above the reference temperature and
denotes the temperature excess above the reference temperature and 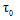 denotes the temperature at any point on the boundary of plate and “a” is the length of a side of square plate.The temperature dependence of the modulus of elasticity for most of engineering materials can be expressed in this
denotes the temperature at any point on the boundary of plate and “a” is the length of a side of square plate.The temperature dependence of the modulus of elasticity for most of engineering materials can be expressed in this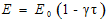
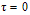 and
and 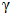 is the slope of the variation of E with. The modulus variation (2.8) become
is the slope of the variation of E with. The modulus variation (2.8) become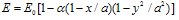
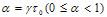 thermal gradient.It is assumed that thickness also varies in two directions i.e. linear in one direction and parabolic in another direction as shown below:
thermal gradient.It is assumed that thickness also varies in two directions i.e. linear in one direction and parabolic in another direction as shown below: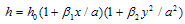
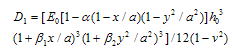
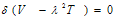
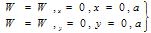
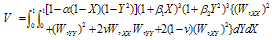
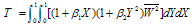
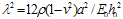 is a frequency parameter.Equation consists two unknown constants i.e. A1 & A2 arising due to the substitution of W. These two constants are to be determined as follows
is a frequency parameter.Equation consists two unknown constants i.e. A1 & A2 arising due to the substitution of W. These two constants are to be determined as follows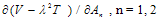
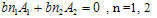
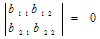


 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML