G. M. Moatimid , Rehab M. El –Shiekh , Abdul-Ghani A. A. H. Al-Nowehy
Department of Mathematics, Faculty of Education, Ain Shams University Heliopolis, Cairo, Egypt
Correspondence to: Rehab M. El –Shiekh , Department of Mathematics, Faculty of Education, Ain Shams University Heliopolis, Cairo, Egypt.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
In this paper, the modified Kudryashov method (the rational Exp-function method) with the aid of symbolic computation has been applied to obtain exact solutions of the (2+1)-dimensional modified Korteweg-de Vries equations (mKdV) and nonlinear Drinfeld-Sokolov system. New exact solitary wave solutions are obtained with comparison of other solutions obtained before in literature.
Keywords:
(2+1)-Dimensional Korteweg-De Vries (Mkdv) Equation, Nonlinear Drinfeld-Sokolov System, The Modified Kudryashov Method, Solitary Solutions
Cite this paper:
G. M. Moatimid , Rehab M. El –Shiekh , Abdul-Ghani A. A. H. Al-Nowehy , "Modified Kudryashov Method for Finding Exact Solutions of the (2+1)-Dimensional Modified Korteweg-De Vries Equation and Nonlinear Drinfeld-Sokolov System", American Journal of Computational and Applied Mathematics , Vol. 1 No. 2, 2011, pp. 101-104. doi: 10.5923/j.ajcam.20110102.20.
1. Introduction
Nonlinear partial differential equations have an important place in the study of nonlinear optics, elasticity theory and plasma physics. As an important aspect of nonlinear science known of these are solitary waves.In this paper, we going to find solitary wave solutions for the (2 + 1)-dimensional modified Korteweg-de Vries equations equation[1].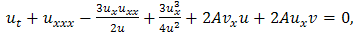 | (1.1a) |
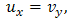 | (1.1b) |
with A being an arbitrary constant, Eqs. (1.1a) and (1.1b) studied using variable separation and nonlinear phenomena[1] and it possesses Painlevé property[2, 3].Also, in this paper, we aim to cast light on the Drinfeld–Sokolov system which is given by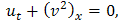 | (1.2a) |
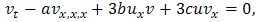 | (1.2b) |
where a, b and c are constants. This system was introduced by Drinfeld and Sokolov as an example of a system of nonlinear equations possessing Lax pairs of a special form[4-6].In this paper, we use the modified Kudryashov method (the rational Exp-function method)[7-9] to obtain new exact solitary wave solutions of the (2+1)-dimensional Korteweg-de Vries (mKdV) equation and the nonlinear Drinfeld-Sokolov system.
2. The Modified Kudryashov Method
To illustrate the basic idea of the modified Kudryashov method, we first consider a general form of nonlinear equation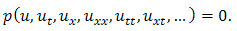 | (2.1) |
where P is a polynomial function with respect to the indicated variables or some function can be reduce to a polynomial function by using some transformation.Making use of the travelling wave transformation 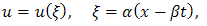 | (2.2) |
where 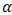 and
and 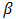 are arbitrary constants to be determined later. Then Eq. (2.1) reduces to a nonlinear ordinary differential equation (ODE)
are arbitrary constants to be determined later. Then Eq. (2.1) reduces to a nonlinear ordinary differential equation (ODE)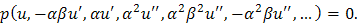 | (2.3) |
We shall seek a rational function type solution for a given partial differential equation, in terms of exp (ξ), of the following form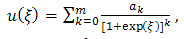 | (2.4) |
where  are constants to be determined to form the solution of (2.1).We can determine m by balance the linear term of the highest order in (2.3) with the highest order nonlinear term.Differentiating (2.4) with respect to ξ, introducing the result into Equation (2.3), and setting the coefficients of the same power of
are constants to be determined to form the solution of (2.1).We can determine m by balance the linear term of the highest order in (2.3) with the highest order nonlinear term.Differentiating (2.4) with respect to ξ, introducing the result into Equation (2.3), and setting the coefficients of the same power of 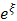 equal to zero, we obtain algebraic equations. The rational function solution of the Equation (2.1) can be solved by obtaining
equal to zero, we obtain algebraic equations. The rational function solution of the Equation (2.1) can be solved by obtaining 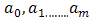 from this system[6].
from this system[6].
3. Solutions of (2+1)-Dimensional Modified Korteweg-De Vries Equation
Eq. (1) can be rewritten as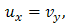 | (3.1b) |
By using the transformation where α, β and γ are arbitrary constant, then Eqs. (3.1a) and (3.1b) become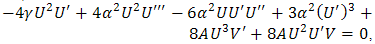 | (3.3a) |
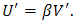 | (3.3b) |
In order to determine values of m and n , we balance the linear term of the highest order partial derivative terms and the highest order nonlinear terms in Eq. (3.3a) and (3.3b) , then we get m=n=2. By using the rational function in exp (ξ), we may choose the solutions of (3.3a) and (3.3b) in the form 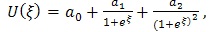 | (3.4a) |
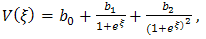 | (3.4b) |
where 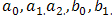 and
and 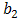 are arbitrary constants to be determined later
are arbitrary constants to be determined later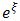 Differentiating (3.4a) and (3.4b) with respect to ξ introducing the result into equations (3.3a) and (3.3b), and setting the coefficients of the same power of
Differentiating (3.4a) and (3.4b) with respect to ξ introducing the result into equations (3.3a) and (3.3b), and setting the coefficients of the same power of 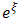 equal to zero, we obtain these algebraic equations
equal to zero, we obtain these algebraic equations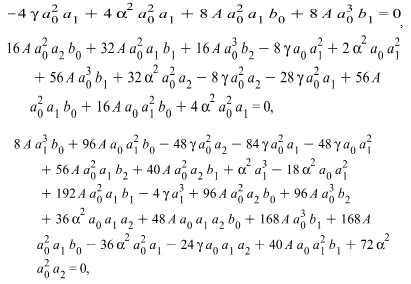
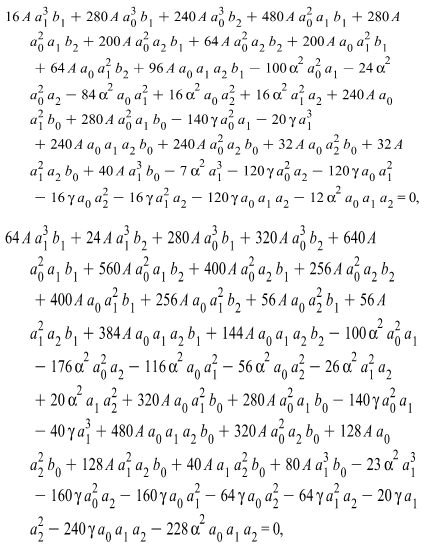
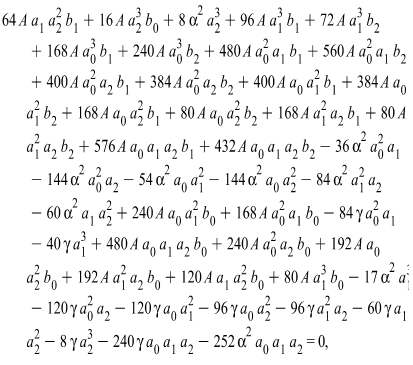
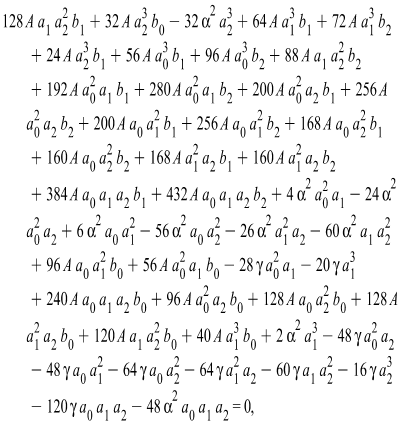
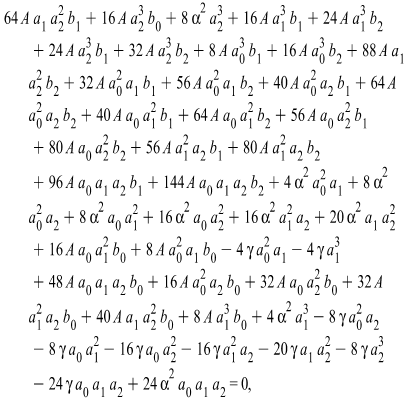
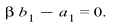 | (3.5) |
Solving the system of algebraic equations (3.5) with the aid of Maple, we obtain two cases of solutionsCase 1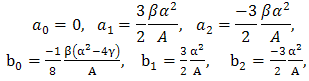 | (3.6) |
By back substitution we get the following new exact solution for the (2+1)-dimensional mKdV equation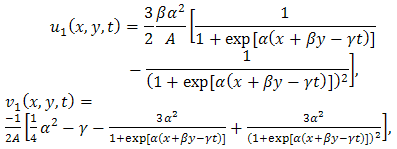 | (3.7) |
Case 2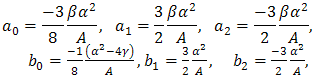 | (3.8) |
By back substitution new exact solution for the (2+1)-dimensional modified Korteweg-de Vries equation is obtained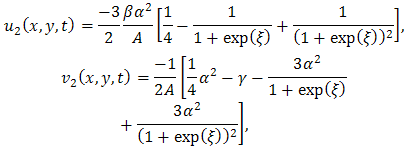 where
where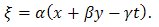 | (3.9) |
4. Solutions for Nonlinear Drinfeld-Sokolov System
Let 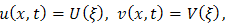 where
where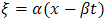 | (4.1) |
Eqs. (1.2a) and (1.2b) becomes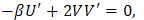 | (4.2a) |
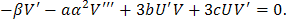 | (4.2b) |
In order to determine values of m and n, we balance the highest order linear terms with the highest order nonlinear terms in Eqs. (4.2a) and (4.2b), then we get m=2 and n=1. By using the rational function in exp (ξ), we may choose the solutions of (4.2a) and (4.2b) in the form 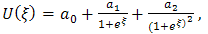 | (4.3a) |
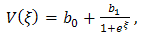 | (4.3b) |
where 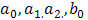 and
and 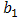 are arbitrary constants to be determined. Differentiating (4.3a) and (4.3b) with respect to ξ introducing the result into equations (4.2a) and (4.2b), and setting the coefficients of the same power of
are arbitrary constants to be determined. Differentiating (4.3a) and (4.3b) with respect to ξ introducing the result into equations (4.2a) and (4.2b), and setting the coefficients of the same power of 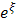 equal to zero, we obtain these algebraic equations
equal to zero, we obtain these algebraic equations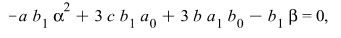
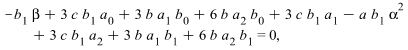
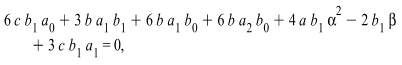
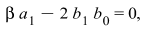
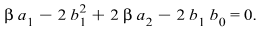 | (4.4) |
Solving the system of algebraic equations (4.4) with the aid of Maple, we obtain the solutions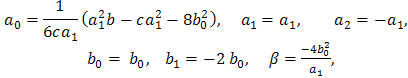
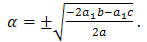 | (4.5) |
Inserting Eqs. (4.5) in to (4.3a) and (4.3b), we get the following solitary wave solutions of Nonlinear Drinfeld-Sokolov system as follows 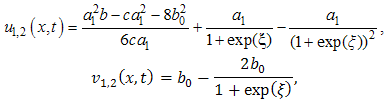 where
where 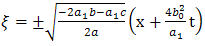 | (4.6) |
5. Conclusions
In this paper, we have applied the modified Kudryashov method (the rational Exp-function method) to obtain new solitary wave solutions of the (2+1)-dimensional modified Korteweg-de Vries equation, and Nonlinear Drinfeld-Sokolov system. The obtained solutions are new and it reflexes how the method is powerful and can be applied on other nonlinear models.
References
| [1] | Yueqian L., Guangmei Wei, Xiaonan Li, Commun Nonlinear Sci Numer Simulat 16 (2011) 603–609. |
| [2] | Zhang R., Shen S., Physics Letters, A 370 (2007) 471–476. |
| [3] | Ferapontov V. E., Diff. Geom. Appl. 11 (1999) 117-128. |
| [4] | Goktas U, J Symb Comput, 24(1997) 591–622. |
| [5] | Wazwaz A., Communications in Nonlinear Science and Numerical Simulation 11 (2006) 311–325. |
| [6] | Biazar J., Ayati Z., Journal of King Saud University – Science (2011) . |
| [7] | Kabir M. M., Khajeh A., Abdi Aghdam E., Yousefi Koma A., Math. Math. Appl., 34 (2011) 213-219. |
| [8] | Yusufoglu E., Bekir A., Computers and Mathematics with Applications, 55 (2008) 1113-1121 |
| [9] | Demiray H., Applied Mathematics and Computation, 154 (2004) 665-670 |

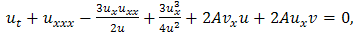
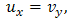
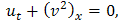
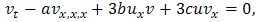
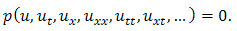
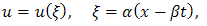
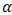 and
and 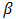 are arbitrary constants to be determined later. Then Eq. (2.1) reduces to a nonlinear ordinary differential equation (ODE)
are arbitrary constants to be determined later. Then Eq. (2.1) reduces to a nonlinear ordinary differential equation (ODE)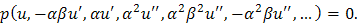
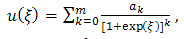
 are constants to be determined to form the solution of (2.1).We can determine m by balance the linear term of the highest order in (2.3) with the highest order nonlinear term.Differentiating (2.4) with respect to ξ, introducing the result into Equation (2.3), and setting the coefficients of the same power of
are constants to be determined to form the solution of (2.1).We can determine m by balance the linear term of the highest order in (2.3) with the highest order nonlinear term.Differentiating (2.4) with respect to ξ, introducing the result into Equation (2.3), and setting the coefficients of the same power of 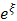 equal to zero, we obtain algebraic equations. The rational function solution of the Equation (2.1) can be solved by obtaining
equal to zero, we obtain algebraic equations. The rational function solution of the Equation (2.1) can be solved by obtaining 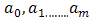 from this system[6].
from this system[6].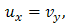
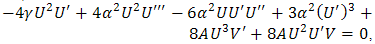
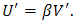
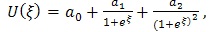
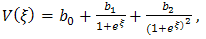
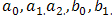 and
and 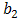 are arbitrary constants to be determined later
are arbitrary constants to be determined later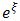 Differentiating (3.4a) and (3.4b) with respect to ξ introducing the result into equations (3.3a) and (3.3b), and setting the coefficients of the same power of
Differentiating (3.4a) and (3.4b) with respect to ξ introducing the result into equations (3.3a) and (3.3b), and setting the coefficients of the same power of 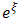 equal to zero, we obtain these algebraic equations
equal to zero, we obtain these algebraic equations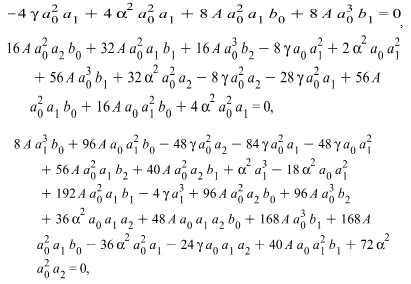
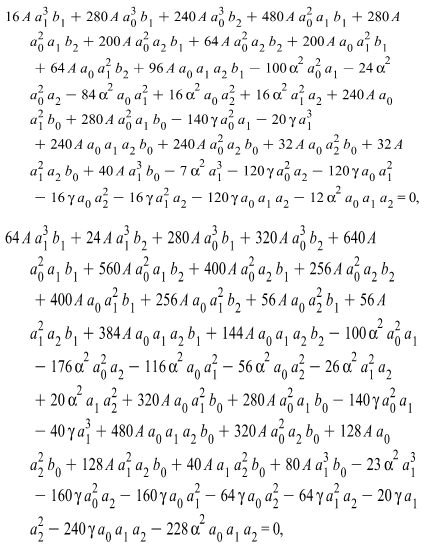
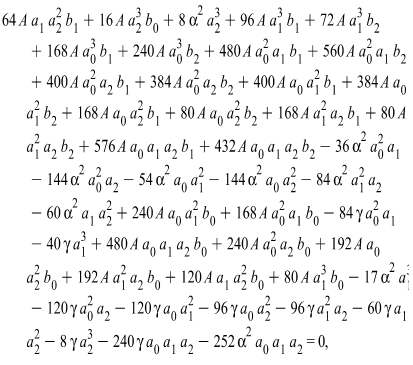
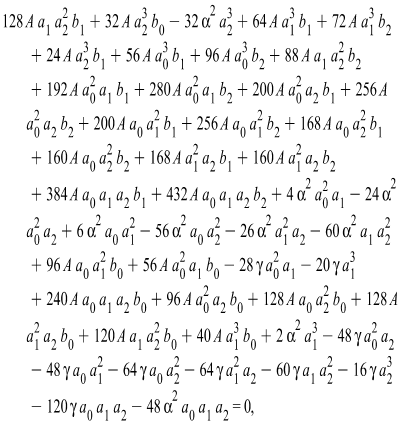
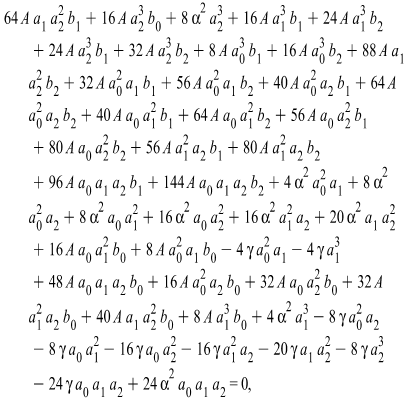
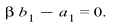
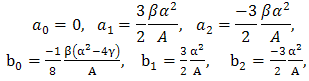
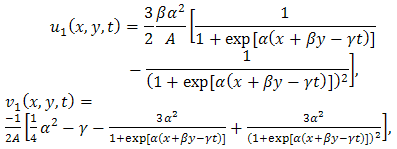
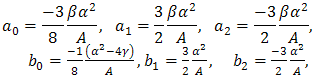
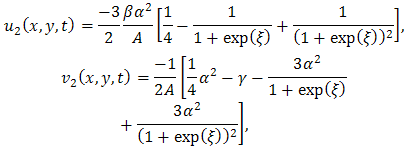 where
where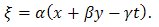
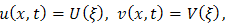 where
where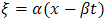
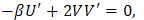
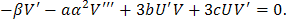
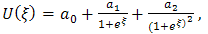
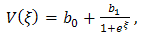
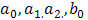 and
and 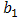 are arbitrary constants to be determined. Differentiating (4.3a) and (4.3b) with respect to ξ introducing the result into equations (4.2a) and (4.2b), and setting the coefficients of the same power of
are arbitrary constants to be determined. Differentiating (4.3a) and (4.3b) with respect to ξ introducing the result into equations (4.2a) and (4.2b), and setting the coefficients of the same power of 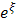 equal to zero, we obtain these algebraic equations
equal to zero, we obtain these algebraic equations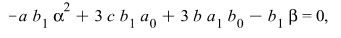
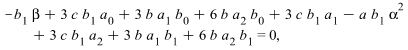
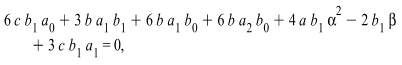
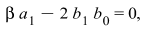
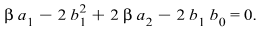
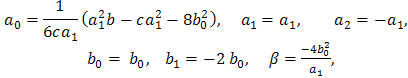
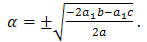
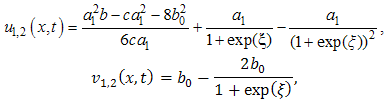 where
where 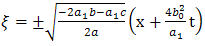
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML