1. Introduction

In , population census usually carried out at ten year interval of time is the most important source of data on size, structure and distribution of population by region or any other demographic and socio-economic phenomena. The Government and Non-government organizations do require the up-to-the-minute information on population. As a consequent, one can easily utilize to formulate realistic devices for development for the present as well as future time. The Government along with demographers is not only the users of population but also trade unions, social organizations, university and other social research institutes and centers, market research analysis, housing developers and business communities frequently do need these estimates for their individual purposes. Population or population by region, religion, age and sex is used to serve as the denominator for the estimation of socio-demographic, health and development related indicators. For that reason, population should be accurate as well as error free for the estimation of different indicators. But not only in but also in any developing countries census population are tremendously affected by various types of errors. So, these might be removed by fitting mathematical model. Islam (2003) mentioned that age structure for male, female and both sexes population of follows either negative exponential model or modified negative exponential model. Islam et al. (2003)reported that age related population for male of in 1991 follows modified negative exponential model. Islam (2004) showed that proportion of married women of in the reproductive life span follow 3^rd degree polynomial model. It was observed that age structure for population of both sexes of follows negative exponential model (Islam et al., 2005). In Islam (2007), it was investigated that the age specific marital fertility rates (ASMFRs) in rural area of follows 2nd degree polynomial model and simple linear regression model where as forward cumulative ASMFRs follows 3rd degree polynomial model.

At this juncture, an attempt would be made to mull over the pattern for cumulative population of in 2001 census using mathematical model. Therefore, the fundamental objectives of this study are as follows:

i) to build up some mathematical models for male and female forward cumulative population of in 2001 census, and

ii) to apply CVPP to test the adequacy of the model.

This paper is divided into five divisions. Introduction is included in the first section. Second section is data and data source of the study. Section three contains methods and various methodological issues in which data smoothing, model building, validation technique of model and F-test are described. Results of model fittings and discussion are narrated in section four. As a final point, conclusion of this study is in division five.

2. Data and Data Source of the Study

To fulfill the objectives mentioned in the introduction section of this manuscript, the secondary data on population for male, female and both sexes of by age group in years have been taken from 2001 census (BBS, 2003). These have been utilized as raw materials in the present study and shown in Table 1.

3. Methods and Various Methodological Issues

3.1. Data Smoothing

The cumulative population for male, female and both sexes by age group in years smoothed before going to fit the mathematical model to this data set. For this, using the Package Minitab Release 12.1 by the latest smoothing method named “4253H, twice” (Velleman, 1980) is employed here. After that, the smoothed data are used to fit model and these smoothed data have been launched in Table 1.

3.2. Model Building

If the forward cumulative distribution of population by age group is plotted in the graph paper then it can be seen that cumulative distribution of population are distributed by polynomial model in terms of ages. Therefore, an n^th degree polynomial model is treated and the structural formation of the model is addressed by

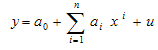(Montgomery and Peck, 1982)

Where, x is the mean value of the age group; y is forward cumulative distribution of population; is the constant; is the coefficient of (i =1, 2, 3, ..., n) and u is the stochastic error term of the model. Here, a suitable n is chosen such that the error sum of square is minimum.

3.3. Validation Technique of Model

To probe the validity of these models, the CVPP,, is applied. The mathematical formula for CVPP is known by

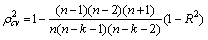Where, n is the number of classes, k is the number of explanatory variables in the model and the cross-validated R is the correlation between observed and predicted values of the dependent variable (Stevens, 1996). The shrinkage of the model is equivalent to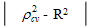; where 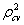is CVPP and R² is the coefficient of determination of the model. Moreover, 1-shrinkage is the stability of R² of the model. The estimated CVPP analogous to their R² and information on model fittings are presented in Table 2. It was informed that CVPP was also employed as validation method by Islam (2003 and 2007) and Islam et al. (2003 and 2005).

Table 1. Observed Population for Male, Female and Both Sexes of Bangladesh in 2001 Census by Age Group and Their Forward Cumulative Distribution (in thousands) Age Group Observed Smoothed Predicted Male Female Both Sexes Male Female Both Sexes Male Female Both Sexes 0-4 8362 7724 16086 8425 7903 16273 8518 7264 15775 5-9 8822 7956 16778 16728 15658 32259 16789 15833 32452 10-14 8420 7432 15852 24437 22933 47105 24182 23421 47297 15-19 6292 5672 11963 31009 29532 60117 30748 30087 60418 20-24 4859 6057 10916 36470 35541 71497 36535 35891 71922 25-29 4895 5865 10760 41272 40972 81673 41594 40893 81915 30-34 4313 4436 8748 45681 45603 90644 45975 45152 90506 35-39 4204 3795 7998 49660 49278 98259 49726 48730 97800 40-44 3426 2774 6200 53051 52081 104445 52898 51685 103906 45-49 2610 1991 4601 55772 54221 109305 55540 54078 108930 50-54 2175 1826 4002 57880 55897 113099 57703 55969 112979 55-59 1309 1047 2356 59494 57209 116034 59435 57416 116161 60-64 1529 1300 2829 60732 58198 118254 60787 58481 118583 65-69 814 629 1443 61686 58937 119941 61808 59223 120351 70-74 926 700 1626 62417 59513 121244 62548 59702 121573 75-79 358 258 616 62994 59994 122302 63057 59978 122356 80+ 581 496 1076 63519 60446 123280 63383 60111 122807

Table 2. Information on Model Fittings and Corresponding CVPP of These Fitted Models

3.4. F-test

To find out the measure of overall significance level of the fitted models as well as the significance of R² , the F-test is employed here. The F-test is given by 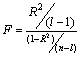with (l-1, n-l) degrees of freedom (d.f.).

Where, l = the number of parameters is to be estimated, n is the number of cases and R² is the coefficient of determination of the model (Gujarati, 1998).

4. Results of Model Fittings and Discussion

The fitted model for forward cumulative distribution of population for male of in 2001 is:

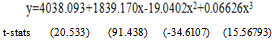(1)

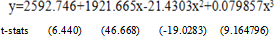The fitted model for forward cumulative population for female of in 2001 is:

(2)

The fitted model for forward cumulative distribution of population for both sexes of in 2001 is:

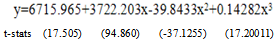(3)

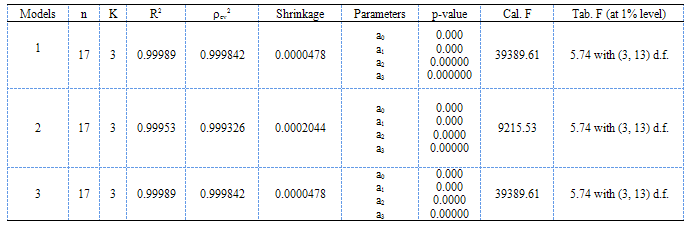
The information on model fittings and estimated CVPP, , corresponding to their R² of these models is shown in Table 2. From this table it appears that all the fitted models (1) - (3) are highly cross- validated and their shrinkages are 0.0000478, 0.0002044 and 0.0002044 respectively. Moreover, it is found that the parameters of the fitted model (1) - (3) are highly statistically significant with large proportion of variance explained. Moreover, these models are stable more than 99%. The stability of R² of these models is more than 99%.

The calculated values of F statistic for the models (1) - (3) are 39389.61, 9215.53 and 39389.61 with (3, 13) d.f. respectively whereas the analogous tabulated values are only 5.74 at 1% level of significance. Therefore, from these statistics it is seen that these models and their analogous R² are highly statistically significant. Hence, the fits of these models are well.

5. Conclusions

In this study, it is observed that forward cumulative distribution of male, female and both sexes population follow 3rd degree polynomial model, i. e., cubic polynomial models containing four parameters. Hope one might be used these predicted population of in 2001 census for further higher study as more smoothened as well as more reliable data than that of observed data aggregate.