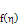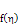Y. M. Aiyesimi 1, Olorunsola O. Niyi 2
1Department of Mathematics/Statistics. Federal University of Technology Minna, Nigeria
2Department of Mathematics. Federal College of Education Kontagora, Nigeria
Correspondence to: Olorunsola O. Niyi , Department of Mathematics. Federal College of Education Kontagora, Nigeria.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
This paper applied the variational iterative method to solve the problem of the two-dimensional incompressible laminar boundary layer flow over a flat plat also called the Blasius problem. The problem is governed by the Navier-Stokes and continuity equations which were first transformed into an ordinary differential equation using similarity transforms and the resulting problem solved using variational iterative method. The results obtained for the similarity stream function and velocity were tabulated and were highly comparable in terms of accuracy with that obtained by Ganji et al. (2009) who studied the same problem using the homotopy perturbation technique and results obtained by Blasius. The results were found to be very accurate especially for η ≤ 4 when using the variational iterative method. The method is convenient as it greatly reduces the amount of computational work.
Keywords:
Variational Iterative Method, Laminar Flat Plate, Boundary Layer, Blasius Flow
Cite this paper:
Y. M. Aiyesimi , Olorunsola O. Niyi , "Computational Analysis of the Non – Linear Boundary Layer Flow over a Flat Plate Using Variational Iterative Method (VIM)", American Journal of Computational and Applied Mathematics , Vol. 1 No. 2, 2011, pp. 94-97. doi: 10.5923/j.ajcam.20110102.18.
1. Introduction
Steady flow of viscous incompressible fluids has attracted considerable attention in recent years due to its crucial role in numerous science and engineering applications. In particular, the classical boundary layer flow past a static flat plate problem has attracted considerable interest of many researchers since introduced by Blasius (1908). Since then, the problem has been analyzed by various authors; Falkner & Skan (1931), Asaithambi (2005), Zhang & Chen (2009), Ganji et al (2009) and several others in order to obtain results of the Blasius equation. We are to solve the problem using He’s Variational iterative method.The Variational iterative method (VIM) which is based on the use of restricted variations and correction functional has found a wide application for the solution of linear and nonlinear ordinary and partial differential equations. VIM has been used for solving the 7th order Swada-kotera equations (Hosein et al, 2008), Burger’s and coupled Burger’s equation (Abdou & Soliman, 2005), linear and non-linear Klien Gordon equations (Hussain & Khan, 2010), system of integro-differential equations (Matinfari & Gambari, 2010), Sturm-Liouville equations (Neamaty & Darzy, 2010) and several other linear and non-linear problems.Our aim is to apply the VIM to find solution to the laminar boundary flow over a flat plate which is one of the very popular problems arising in fluid mechanics. We employ the use of a similarity transformation of the Navier – Stokes and continuity equations to obtain an ordinary differential equation with the necessary boundary conditions. This problem is solved using VIM in this paper and the results are then compared to those obtained by Ganji et al (2009) using homotopy perturbation method (HPM) and Blasius (1908).
2. He’s Variational Iteration Method (VIM)
For the purpose of illustrating the methodology of He’s variational iteration method, we begin by considering a differential equation in the formal form,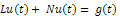 | (1.1) |
where L is a linear operator, N a nonlinear operator and g(t) is the given continuous function. According to He (2006) He & Wu (2007), we can construct a correction functional as follows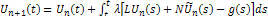 | (1.2) |
where λ is a general Lagrangian parameter, which may be optimally identified in the variational theory. The subscript n denotes the nth order approximation, 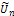 is considered as a restricted variation i.e.,
is considered as a restricted variation i.e., 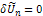 .We therefore determine λ as defined above after which the successive approximations Un+1(x, t), n ≥ 0 of the solution U(x, t) will be readily obtained upon using the computed λ from a selective function U0. Consequently, the solution is given by
.We therefore determine λ as defined above after which the successive approximations Un+1(x, t), n ≥ 0 of the solution U(x, t) will be readily obtained upon using the computed λ from a selective function U0. Consequently, the solution is given by 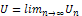 | (1.3) |
The solution of the linear problems can be solved in a single iteration step due to the exact identification of the Lagrange multiplier. The method also provides an efficient method for handling nonlinear behaviour; a few iterations can be used to achieve a high degree of accuracy.
3. Materials and Method
Equations of the flow in the boundary layer over a flat plate are governed by the continuity equation; 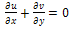 | (2.1) |
and the reduced Navier- Stokes equation 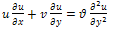 | (2.2) |
where u and v are respectively the components of the velocity vector and 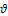 represents the kinematic viscosity of the fluid. Boundary conditions are
represents the kinematic viscosity of the fluid. Boundary conditions are 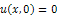 | (2.3a) |
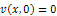 | (2.3b) |
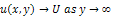 | (2.3c) |
where 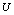 is the constant speed of the flow outside the boundary layer.To eliminate the continuity equation, we introduce the stream function 𝜓 such that;
is the constant speed of the flow outside the boundary layer.To eliminate the continuity equation, we introduce the stream function 𝜓 such that;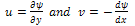 | (2.4) |
Applying this to (1.1) and (1.2) yields;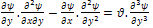 | (2.5) |
In order to simplify the above problem, the Blasius similarity transform is applied in order to convert (2.5) into an ordinary differential equation.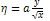 | (2.6a) |
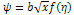 | (2.6b) |
Where a and b are constants and are chosen to make  and
and 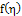 dimensionless,
dimensionless,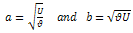 | (2.6c) |
Therefore, η is called the dimensionless similarity variable and f(η ) is called the dimensionless stream function.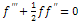 | (2.7) |
with the boundary conditions;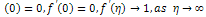 | (2.8) |
The equation (2.7) together with boundary conditions (2.8) is also called the Blasius problem.To solve the problem using VIM we reformulate by using the dependent variable;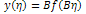 | (2.9) |
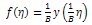 | (2.10) |
Hence equation (2.7) becomes,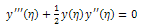 | (2.11) |
and the boundary conditions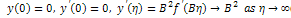 | (2.12) |
hence, 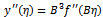 imposing the condition,
imposing the condition,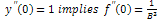 | (2.13) |
Solution to equation (2.11) with boundary conditions (2.12) using variational iterative method (VIM) is obtained as follows.The correction functional is written as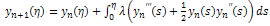 | (2.14) |
Making the correction functional stationary with respect to 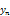 and noting that
and noting that 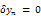
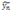 is a restricted variation, therefore
is a restricted variation, therefore 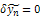
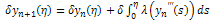 | (2.16) |
The stationary conditions are;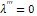 | (2.19a) |
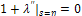 | (2.19b) |
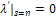 | (2.19c) |
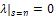 | (2.19d) |
From (2.19b);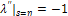 Applying (2.19a), (2.19c) and (2.19d) as natural conditions yields;
Applying (2.19a), (2.19c) and (2.19d) as natural conditions yields;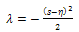 | (2.20) |
As a result we obtain the following iteration formula;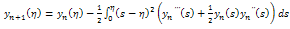 | (2.21) |
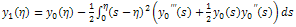 | (2.22) |
From equation (2.21) above we have the following results;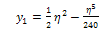 | (2.23) |
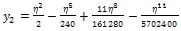 | (2.24) |
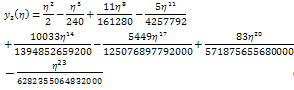 | (2.25) |
Assuming 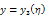 ,
,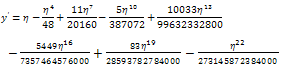 | (2.26) |
Fro m equation (2.10), 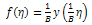 Also from (2.13)
Also from (2.13)  , then
, then | (2.28) |
 | (2.29) |
The result obtained is compared with results obtained by Ganji et al (2009) who used the homotopy perturbation method to solve the same problem and compared results with that obtained by Blasius.Ganji et al (2009) assumed the value  and obtained the following series;Similarly, we also take the value σ = 0.332057 in equation (34) and obtained the following series;
and obtained the following series;Similarly, we also take the value σ = 0.332057 in equation (34) and obtained the following series; | (2.29) |
Table 1. Comparison of results obtained using the present method (VIM) with Homotopy perturbation method by Ganji et al. and Blasius for
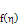 |
| | f(η) | | (η) | Blasius | Ganji et al (HPM) | VIM | | 0 | 0 | 0 | 0 | | 0.5 | 0.0415 | 0.0415 | 0.0415 | | 1.0 | 0.1656 | 0.1655 | 0.1656 | | 1.5 | 0.3701 | 0.3701 | 0.3701 | | 2.0 | 0.6500 | 0.6500 | 0.6500 | | 2.5 | 0.9963 | 0.9962 | 0.9963 | | 3.0 | 1.3964 | 1.3968 | 1.3966 | | 3.5 | 1.8377 | 1.8350 | 1.8361 | | 4.0 | 2.3057 | 2.2897 | 2.2966 |
|
|
Table 2. Comparison of results obtained using the present method (VIM) with Homotopy perturbation method by Ganji et al. and Blasius for
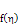 |
| | f’(η) | | (η) | Blasius | Ganji et al (HPM) | VIM | | 0 | 0 | 0 | 0 | | 0.5 | 0.1659 | 0.1658 | 0.1659 | | 1.0 | 0.3298 | 0.3298 | 0.3298 | | 1.5 | 0.4868 | 0.4867 | 0.4868 | | 2.0 | 0.6298 | 0.6297 | 0.6298 | | 2.5 | 0.7513 | 0.7511 | 0.7512 | | 3.0 | 0.8460 | 0.8445 | 0.8451 | | 3.5 | 0.9130 | 0.9027 | 0.9070 | | 4.0 | 0.9555 | 0.9028 | 0.9262 |
|
|
4. Results
We compare results obtained through Variational Iterative method (VIM) with that of Ganji et al (Homotopy Perturbation Method) and Blasius in Ganji et al(2009) for f(η) and f’(η) in Table1 and Table 2 below. | Chart 1. showing comparison of result of Blasius, Ganji et al and VIM for 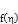 |
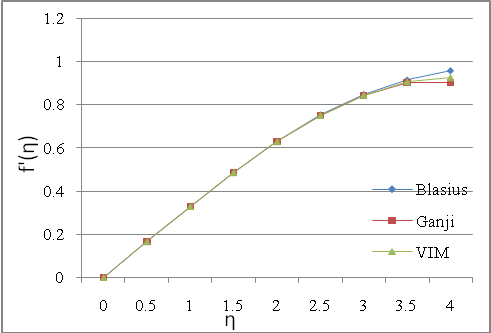 | Chart 2. showing comparison of result of Blasius, Ganji et al and VIM for 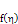 |
5. Discussion
In this paper, we have used the method of iterative variational method to investigate the problem posed by the non – linear boundary layer flow over a flat plat and the results obtained are highly comparable in term of accuracy with that obtained by Ganji et al who studied the same problem using the homotopy perturbation technique. The results were found to be very accurate especially when η ≤ 4 using the variational iterative method.
References
| [1] | Abdou, M. A. & Soliman, A. A. (2005). Variational Iterative Method for solving Burger’s and coupled Burger’s equations. Journal of computer and applied mathematics. 181(2005), 245 – 251 |
| [2] | Asaithambi, A. (2005). Solution of the Falkner-Skan equation by recursive evaluation of Taylor coefficients. J. Compute. Appl. Math. 176, 203-214(2005) |
| [3] | Blasius, H. (1908) The boundary layers in fluid with little friction (in German). Zeitschrift fur Mathematikund Physik . 56(1):1-37 (1908) ; English translation available as NACATM 1256 , February(1950) |
| [4] | Fazio, R. (1996). A novel approach to the numerical solution of boundary value problems on infinite intervals. SIAM J. Number. Anal. 33:1473–1483 (1996) |
| [5] | Ganji D. D, Babazadeh H, Noori H, Pirouz M.M, & Janipour M. (2009). An application of homotopy perturbation method for non-linear Blasius equation to boundary layer flow over a flat plate. International journal of Nonlinear Science Vol.7(2009) No.4,pp.399-404 |
| [6] | He, J. H. (2006). Variational iteration method: Some recent results and new interpretations. Journal of Computational & Applied Mathematics, 10 (2006) 07−09 |
| [7] | He, J. H. & Wu, X. H. (2007). Variational iteration method: New development and applications. International Journal of Computers and Mathematics with Applications. 54 (2007) 881–894 |
| [8] | Hosien J, Allabaksh Y, Jawad V, Dawwod D. G. (2008). Application of He’s Variational Iterative Method for solving seventh order Sawada-Kotera equations. Applied Mathematical Sciences. Vol. 2 (2008), No. 10, 471-477 |
| [9] | Hussain, M. & Majid K. (2010). A Variational Iterative Method for solving the linear and non-linear Klien-Gordon Equations. Applied MathematicalSciences. Vol. 4 (2010), No. 39, 1931 – 1940 |
| [10] | Karimi P,Eshghi N,Ganji D. D,Rostamian M. & Daniali H. M.(2008) A modified method to identification of Lagrange multipliers. Retrieved 14/11/2010 fromhttp://iopscience.iop.org/1742-6596/96/1/012076 |
| [11] | Kıymaz, O & Cetinkaya, A. C.(2010). Variational Iteration Method for a Class of Nonlinear Differential Equations. International Journal of Contemporary Mathematical Sciences, 5(2010), 1819 - 1826 |
| [12] | Mantifar, M. &Ghanbari, M. (2010).Solution of system of integro – differential equations by Variational Iterative Method. Journal of mathematics and computer science. Vol. 1, No. 2 (2010), 47 – 57 |
| [13] | Neamaty, A. & Darzy, R. (2010). Comparison between the Variational Iterative Method and Homotopy perturbation method for Sturm – Liouville D.E |
| [14] | Zhang, J. & Chen, B. (2009). An iterative method for solving the Falkner-Skan Equation, Applied Mathematics and Computation, 210, N0.1, 215-222 |

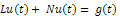
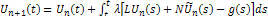
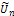 is considered as a restricted variation i.e.,
is considered as a restricted variation i.e., 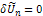 .We therefore determine λ as defined above after which the successive approximations Un+1(x, t), n ≥ 0 of the solution U(x, t) will be readily obtained upon using the computed λ from a selective function U0. Consequently, the solution is given by
.We therefore determine λ as defined above after which the successive approximations Un+1(x, t), n ≥ 0 of the solution U(x, t) will be readily obtained upon using the computed λ from a selective function U0. Consequently, the solution is given by 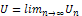
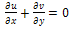
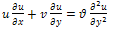
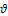 represents the kinematic viscosity of the fluid. Boundary conditions are
represents the kinematic viscosity of the fluid. Boundary conditions are 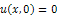
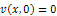
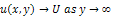
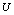 is the constant speed of the flow outside the boundary layer.To eliminate the continuity equation, we introduce the stream function 𝜓 such that;
is the constant speed of the flow outside the boundary layer.To eliminate the continuity equation, we introduce the stream function 𝜓 such that;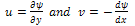
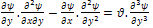
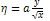
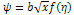
 and
and 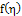 dimensionless,
dimensionless,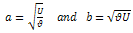
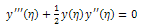
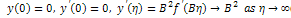
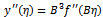 imposing the condition,
imposing the condition,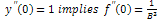
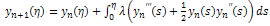
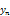 and noting that
and noting that 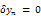
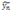 is a restricted variation, therefore
is a restricted variation, therefore 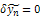
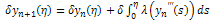
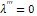
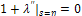
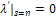
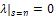
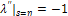 Applying (2.19a), (2.19c) and (2.19d) as natural conditions yields;
Applying (2.19a), (2.19c) and (2.19d) as natural conditions yields;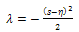
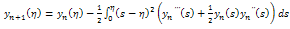
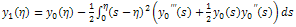
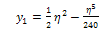
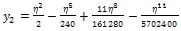

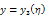 ,
,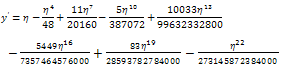
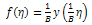 Also from (2.13)
Also from (2.13) 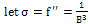 , then
, then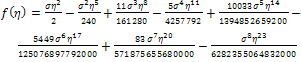

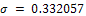 and obtained the following series;Similarly, we also take the value σ = 0.332057 in equation (34) and obtained the following series;
and obtained the following series;Similarly, we also take the value σ = 0.332057 in equation (34) and obtained the following series;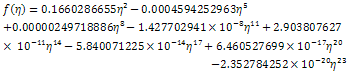

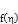

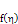
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML